地铁区间小净距上叠风道施工力学效应研究

靳晓光，杨清亭，邱 锋

(重庆大学 土木工程学院，重庆 400030)

0 引 言

随着西部大开发，轨道交通作为解决公共交通压力的重要工具，在西部大城市取得快速发展。西部特殊的地形地貌，也带来新的问题和研究内容。

地铁隧道大多双线并行，小净距成为一个重要研究内容。小净距隧道历来都是国内众多学者的研究对象。姚勇等[1]研究了在不同开挖方式下小净距隧道的施工力学效应下施工力学行为的较大差异，证明后继隧道施工的开挖方式直接对先行既有隧道产生很大影响；冯兴等[2]用隧洞的应力变形及稳定性分析出发对隧洞的安全稳定性进行了探讨；钟祖良等[3]研究浅埋双侧偏压小净距隧道围岩压力的大小及分布规律， 针对该类型隧道的特点建立了浅埋双侧偏压小净距围岩压力荷载计算的力学模型；郑颖人[4]用有限元的方法分析法研究了无衬砌隧洞围岩的定量稳定性分析质以及有衬砌隧洞时隧洞初衬与二衬的设计计算方法。

风井也是地铁隧道建设的一个重要研究内容，被众多学者研究。J. S. LEE[5]对韩国首尔地铁七号线修建时的一个临时竖井施工过程进行了三维数值分析；张志强等[6]以万梁高速公路马王槽 1 # 隧道为依托，对主隧道与车行横通道组成的空间交叉结构进行了施工过程中的结构力学研究；张鲲[7]依托重庆轨道交通六号线某活塞风井，研究了重庆特殊山地地形条件下隧道的通风配置，通过模拟计算，对山地地形风井进行了特殊研究；XIE Jinshui等[8]依托工程实例，研究了从风井开挖地铁车站的施工工艺及其施工特点。目前大多数风井的研究均针对地铁车站，而对区间风道及其横通道的研究还很少。

笔者依托重庆四号线某施工标段的小净距区间隧道小净距上叠风道段工程施工过程进行深入研究。

1 工程概况

研究工程对象地处重庆渝北区，区间风井位于四号线K15+800至K15+850段，该区域隧道埋深56.52 m。该处地表为约6 m的素填土，下伏厚度为约4 m的风化岩，工程大部分处于砂质泥岩层，局部为砂岩透镜体。局部洞身外侧为外倾结构面，J2层面的组合线与B2为不利组合，但交角较小，并该出涌水量较小，设计围岩等级取为V级。

该段区间隧道开挖断面近似为直径7 m的圆形断面，两区间隧道净距为2.5 m。横通道断面高15.55 m，宽10.90 m，上台阶高5.25 m，截面如图1。

由于工期要求，正线区间和风道同时施工。风道开挖时，会出现深埋区间隧道上覆岩体上表面临空，而上表面距下面的正线区间拱顶仅3.3 m，其效果图见图2。

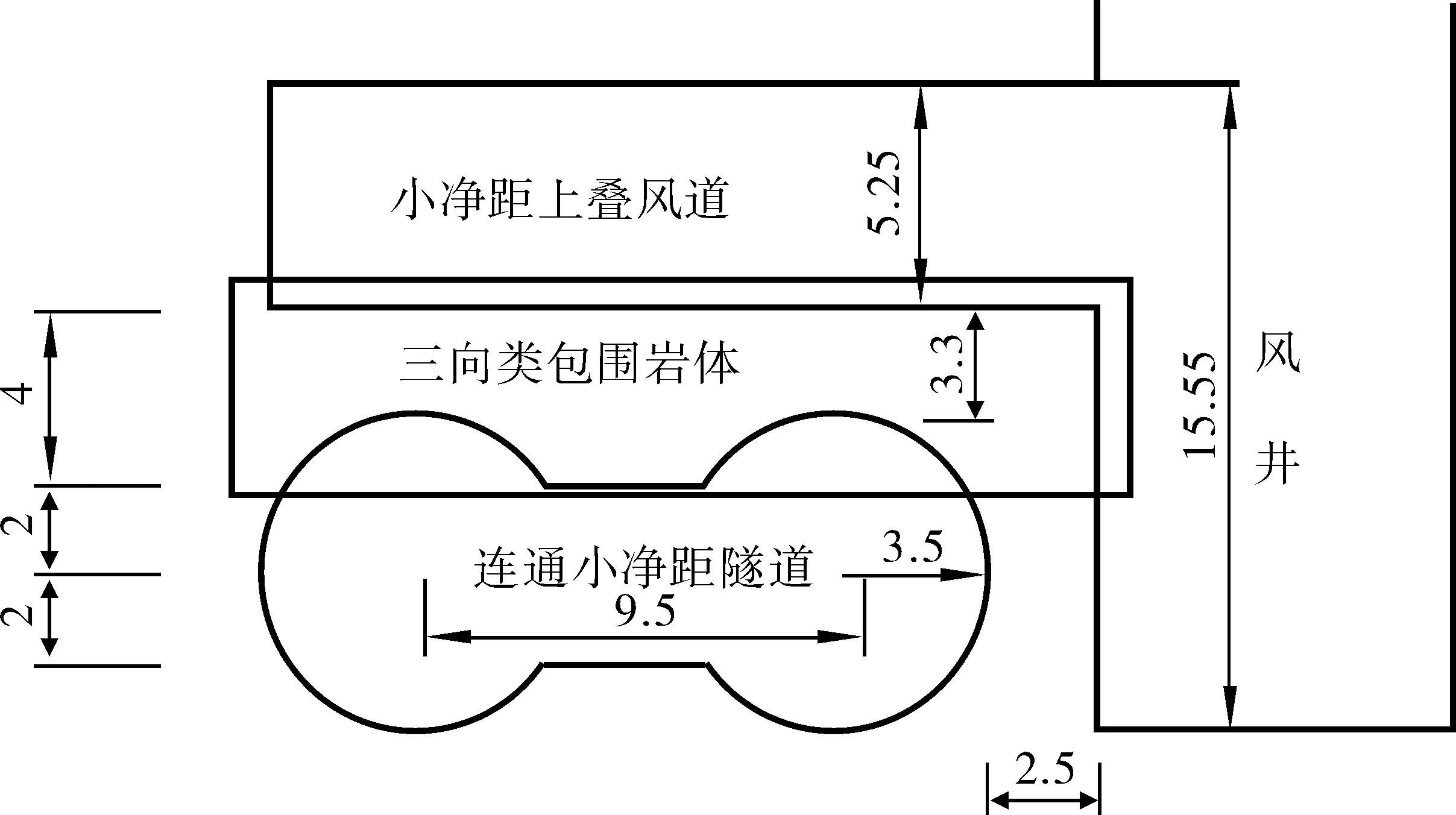
图2 效果图(单位：m)Fig. 2 The renderings

而在施工期间，出现过右线隧道拱顶掉块和拱角开裂现象，加之施工工法特殊，对其分析研究意义重大。

2 二维连通净距隧道分析

正线隧道开挖完成后将形成如图3的二维小净距空间模型。目前国内对该类型连通隧道未得出简化的内力计算方法，笔者将对此做出讨论。

图3 二维连通小净距隧道Fig. 3 Two-dimensional connecting small-distance tunnel

2.1 二维理论分析

根据《公路隧道设计规范》[9]，该区间隧道为小净距隧道。由塌落拱理论可知，当两个隧道净距较小时，其双塌落拱的重合塑性区较大，故可按一个连拱断面时的共同塌落拱考虑。而此处隧道净距很小且两隧道连通，中间岩体解除，故可按一个整体的塌落拱考虑围岩压力。而开挖后中部突出岩体受力较小，故笔者将该洞室模型进行简化，如图4，并结合弹性力学基本知识用平面问题的复变函数解法求解其周边应力。

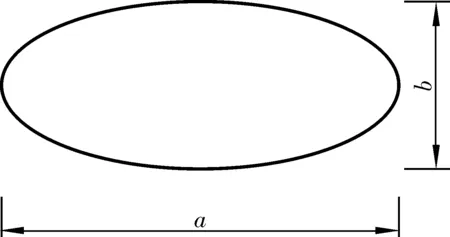
图4 等效椭圆模型Fig. 4 Equivalent elliptical model

根据尺寸等效原则，取椭圆长轴尺寸为两隧道直径与净距之和，短轴尺寸取单个隧道的直径尺寸，如式(1)：

(1)

2.1.1 复变函数公式推导

由于隧道埋深较大，故可将隧道平板上的小椭圆孔问题用平面上的椭圆孔模型求解其应力，如图5。

图5 椭圆孔计算模型Fig. 5 Calculation model of elliptical hole

根据弹性力学复变函数理论[10]，将函数位移、应力和边界条件表示成复变函数形式，并用两个解析函数表示艾里应力函数。具有圆孔的平面域复位势函数见式(2)：

(2)

式中：α为椭圆洞的倾斜角度；φ为与长轴正方向的夹角。

将孔边外部所占的无穷区域(z平面)变成单位圆外围的区域(z=ω(ζ))，并通过复变函数变换和推导，可以得到它的解析函数为式(3)：

(3)

又由边界条件可得式(4)：

(4)

将式(3)代入式(4)并整理后推导得到式(5)：

(5)

将式(3)代入式(4)继续推导可得到式(6)：

(6)

由保角变换推导得到式(7)：

σρ+σφ=4Re[Φ(ζ)]

(7)

由于，存在如式(8)：

(8)

将式(8)代入式(7)并取实部，得到式(9)：

(9)

代入边界条件(ρ=1,σρ=0)，σφ可表示为式(10)：

(10)

取α=0，σφ可表示为式(11)：

(11)

取α=π/2，σφ可表示为式(12)：

(12)

2.1.2 计算应用

在上述公式的基础上，可得出不同角度α下各种姿态椭圆孔的孔边受力。而在前述等效模型中，受来自竖直和水平方向两个角度的力不同，将α分别为0和π/2的两种情况进行叠加，则隧道周边的应力计算公式如式(13)：

(13)

将式(11)、式(12)代入式(13)并整理后得出式(14)：

(14)

式中：m=(a-b)/(a+b)；qV、qH依据《公路隧道设计规范》取值，qH=387 kPa,qV=135.45 kPa。

由二维模型的对称性可知，其应力分布具有x轴对称性，故其0～π的计算结果见表1。

表1 理论计算洞室孔壁应力Table 1 Theoretical calculation of hole wall stress

2.2 二维数值模拟

基于上述推导，运用MIDAS/GTS对该二维模型进行计算，对比验证理论分析正确性。

2.2.1 围岩参数的选取和尺寸选取

重庆市区特殊的山区城市地貌条件下，隧道洞室周边围岩多为节理围岩。根据现场的地质勘察报告和设计说明，参考杜帅等[11]关于山区城市地貌节理围岩力学参数选取办法，考虑岩体节理间距、节理间的岩块中的微裂隙、围岩的内聚力、内摩擦角以及节理强度参数，结合公路隧道设计细则，选用如表2的岩石力学参数。

表2 岩石力学参数Table 2 Parameters of rock mechanics

整个隧道截面，最大尺寸为16.5 m，故二维模拟尺寸为宽96 m，模型岩体深度取110.77 mm，开挖截面位于模型中部，埋至深度取实际值66.02 m，其模型如图6。

图6 二维连通小净距隧道模拟Fig. 6 Two-dimensional simulation of small-distance tunnel

2.2.2 二维模拟结果分析

用GTS NX进行隧道的二维模拟，主要集中对隧道洞室周边围岩应力进行分析，其应力云图如图7。

图7 二维洞室压力云图Fig. 7 Pressure cloud of two-dimensional cavern

若用极坐标表示，从二维计算云图中可以知道最大围岩应力在φ=0和φ=π的洞身边缘处，即与水平方向呈0和π夹角位置。

提取各个角度的应力数值，并与理论计算的应力对比，结果见表3。

表3 理论和模拟应力对比Table 3 Comparison of theoretical and simulated stresses

通过上面理论分析和数值模拟的对比可知，理论计算和数值模拟的结果比较吻合，其应力最大值出现在与水平呈0和π角度的位置。在π/2位置出现差值最大的情况，分析后得出原因是数值模拟该处洞身处突出，出现棱角造成局部应力有所差异，但是相差不大，故可认为上述理论推导和等效模型的适用性。

3 横通道三维模拟

3.1 三维模型建立

二维计算和模拟不能考虑开挖施工步序的影响，固可用三维数值模拟研究施工步序对开挖围岩的力学响应。

本次三维模型建立，取二维模拟时的围岩参数，依据四号线该段风道工程的施工顺序，把三维风道开挖工序分为40个工序，模型在正线区间的长度取为140 m，横通道长度方向取160 m，横通道下方岩体取45 m，则模型高度为111.02 m，建立模型如图8(剖切表示)。

图8 三维模型Fig. 8 Three-dimensional model

3.2 三维模拟数值计算分析

在数值模拟中，选取主要关注的区间隧道、风道和风井的三向类包围的岩体为研究对象，并取其应力(或位移)最大值或变化最大值几个点为重点，分别取为A、B、C、D、E5个点(图9)。

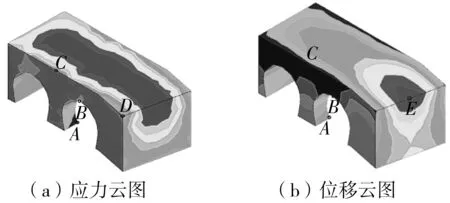
图9 应力云图和位移云图Fig. 9 Stress cloud and displacement cloud

由数值计算结果选取A、B、C、D4个关键点，四点应力累积曲线如图10。

图10 应力累积曲线Fig. 10 Stress accumulation curve

由图10可知，4个点中，A点是整个横通道下薄岩体应力最大的一个点；随着施工开挖步序的进行，应力值不断增大，在工序18时，出现了峰值应力，达到-4 146.79 kPa，直至横通道上台阶开挖完成逐渐稳定至3 532.7 kPa。B、C、D点的应力随着开挖进行持续增大，D点的应力在工序12和24时显著上升后缓慢增长，最终达到-2 842.61 kPa。

统计4个位移关键点A、B、C、E计算数值可得位移曲线图(如图11)。

图11 位移累积曲线Fig. 11 Displacement accumulation curve

由图11可知，E点是整个横通道范围内位移最大的一个点，在整个施工过程中变化较为显著。由于上台阶自重应力的解除和临空面的出现，E点位移显著增长，尤其开挖E点上方岩土体时，呈阶跃式增长，在工序31时达到最大值12.89 mm，最终位移达到11.96 mm。A、B、C3点位移变化趋势大致相同，最终三点位移分别为6.48、-1.54、-0.98 mm。

由此可见施工开挖时，尤其要注意正线区间拱角处A点和横通道上E点的应力和位移监测，为施工提供可靠数据指导。

3.3 现场监测数据分析

依据数值模拟分析所得结论，在工程建设期间，对工程各施工阶段中危险位置的位移和应力进行监测。位移采用设反光材质制作位移监测点，配合全站仪进行监测，应力采用埋设的压力盒进行监测，局部监测点位如图12。

图12 位移监测点位Fig. 12 Displacement monitoring points

在A处开挖完成后埋设压力盒监测A点应力，开始15天每天进行1～2次读数，15天后按一周2～3次的监测频次测量。最后统计整理数据，并和对应的数值模拟结果进行对比，可得到应力累计对比曲线，如图13。

图13 应力对比曲线Fig. 13 Contrast curves of the stress

由图13可知，A点的数值计算应力和监测应力在隧道开挖过程中呈现相同的变化趋势，且其数值也比较接近。由于有时现场的支护较模拟存在滞后，应力释放大，所以整体监测数值较理论数值略小。

在A、E两处开挖完成后及时布设位移监测点位并及时测量，连续3天速率大于0.2 mm/d时按每天一次的频率测量，当小于0.2 mm/d时按一周2～3次的频率测量。统计整理数据，并和对应的数值模拟结果进行对比，可得到位移累计对比曲线，如图14。

图14 位移对比曲线Fig. 14 Contrast curves of the displacement

由图14可知，A、E两点的数值计算位移和监测位移在隧道开挖过程中呈现大体相同的变化趋势，并且其数值也比较接近。由于在风道上台阶开挖后，此处横通道与隧道之间的岩体很薄，故上台阶的施工荷载使实际的回弹位移减小。

通过对比数值计算和监测数据，三维模拟结果能较好的模拟现场实际施工工况，所得结果基本符合实际。

4 结 论

1)由二维理论计算和数值模拟结果对比可知，用椭圆截面代替连通的小净距区间隧道截面是可行的。该等效模型可用于简化计算连通小净距隧道的内力，尤其小净距隧道联络通道处内力。

2)在已开挖正线区间上方开挖小净距风道，对正线区间上方岩体应力有显著影响，尤其风道与风井交接的角点位置，应力显著增加。

3)风道的开挖施工对被风道、区间隧道和风井三向类包围的岩土体有显著影响。由于横通道的开挖，局部约束和应力的解除，整个薄岩层整体呈现回弹趋势。最大位移出现在风道与风井连接面面底边的中点E，所以对该处岩体应加强自稳能力，保证岩层体不产生过大位移。该模拟结果可用于指导同类型上叠风道工程施工。

参考文献(References)：

[1] 姚勇，晏启祥，周俐俐.小净距隧道在不同开挖方式下的力学效应分析[J].西南科技大学学报，2005，20(2)：53-56.

YAO Yong, YAN Qixiang, ZHOU Lili.Study on mechanics effect of small-distance tunnels located at soft ground [J].JournalofSouthwestUniversityofScienceandTechnology, 2005, 20(2): 53-56.

[2] 冯兴，姚仰平，霍海峰.黄土隧洞变形及稳定性分析[J].重庆交通大学学报(自然科学版):2017,36(7): 21-28.

FENG Xing, YAO Yangping, HUO Haifeng. Deformation and stability of loess tunnel [J].JournalofChongqingJiaotongUniversity(NaturalScience): 2017, 36(7): 21-28.

[3] 钟祖良，刘新荣，刘元雪，等.浅埋双侧偏压小净距隧道围岩压力计算与监测分析[J].重庆大学学报，2013，36(2)：63-68.

ZHONG Zuliang, LIU Xinrong, LIU Yuanxue, et al. The pressure calculation and monitoring analysis of surrounding rock mass in shallow tunnels with bilaterally biased small clear spacing [J].JournalofChongqingUniversity, 2013, 36(2): 63-68

[4] 郑颖人.有限元极限分析法在隧洞工程中的应用[J].重庆交通大学学报(自然科学版),2011,30(增刊2):1127-1137.

[5] ZHENG Yingren. Application of finite element limit analysis in tunnel engineering [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2011, 30(Sup2): 1127-1137

[5] LEE J S. An application of three-dimensional analysis around a tunnel portal under construction [J].TunnelingandUndergroundSpaceTechnology, 2009, 24(6):731-738.

[6] 张志强，苏江川，姜元俊.马王槽主隧道与横通道交叉部施工受力特征数值模拟分析[J].公路交通科技，2007，24(1)：109-113.

ZHANG Zhiqiang, SU Jiangchuan, JIANG Yuanjun. Three dimensional fem simulation analysis of construction of intersection of transverse gallery and main tunnel [J].JournalofHighwayandTransporta-

tionResearchandDevelopment, 2007, 24(1): 109-113.

[7] 张鲲.重庆轨道交通6号线一期工程深埋隧道活塞通风竖井设计分析[J].铁路标准设计，2016，60(2).149-152

ZHANG Kun. Design analysis of deep buried tunnel piston ventilation of Chongqing metro line 6 first phase [J].RailwayStandardDesign, 2016, 60(2): 149-152.

[8] XIE Jinshui, BAI Mingzhou, XU Zhaoyi. Study on simulation and stability analysis of subway station excavation from the vertical construction well [J].AdvancedMaterialsResearch, 2011, 250: 1243-1247.

[9] 招商局重庆交通科研设计院有限公司.公路隧道设计规范：JTG D70—2004[S].北京：人民交通出版社，2004.

China Merchants Chongqing Communications Research & Design Institute Co., Ltd.SpecificationsforDesignofHighwayTunnels:JTGD70—2004 [S]. Beijing: China Communications Press, 2004.

[10] 吴家龙.弹性力学[M].北京：高等教育出版社，2001.

WU Jialong.Elasticity[M]. Beijing: Higher Education Press, 2001.

[11] 杜帅，陈力华，靳晓光，等.山区城市环境下节理围岩小净距隧道施工力学研究[J].公路交通技术，2014(6)：53-57.

DU Shuai, CHEN Lihua, JIN Xiaoguang, et al. Research on mechanics in construction of small clearance tunnels of joint wall rocks in mountai-nous city environment [J].TechnologyofHighwayandTransport, 2014(6): 53-57.