介电弹性体卷形换能器设计与参数优化

曹建波 任钰雪 鄂世举 夏文俊 张海艇 朱喜林

(浙江师范大学工学院， 金华 321004)

0 引言

介电弹性体(Dielectric elastomer，DE)是一种具有电活性的弹性体材料，能够在电场作用下改变形状，将电能转换为机械能；同样，它的逆过程也可以用于发电，将机械能转换为电能。早在20世纪90年代，很多国内外学者对其变形特性展开了研究，其中美国斯坦福大学是最早对介电弹性体材料进行研究的机构，PELRINE等[1]研制出应变超过100%的介电弹性体材料，在Science上公布之后，引起了驱动领域学者的关注[2-5]。DE作为一种弹性体材料，具有超大变形、高理论比能量密度、高效率、超短反应时间及高疲劳寿命等特点[6-8]，很多研究学者认为可将DE材料应用于可再生能源发电及微机电系统等领域。目前在发电领域，介电弹性体发电机(Dielectric elastomer generator，DEG)的能量回收效率是无法与一些技术成熟的发电机[9-13]相比的，但是基于它的特点，它能够应用于海洋能、人体能等特殊能量回收，是一种具有广阔发展前途的能量回收技术[14-18]。

本文设计DE卷形换能器，并利用Neo- Hooken模型建立DE卷形换能器的机电耦合模型[19]，基于Matlab/Simulink研究DE卷形换能器的发电特性，以及DE卷形换能器的参数优化(弹簧弹性系数的选择)，并通过实验得出DE卷形换能器的最优参数和其发电特性。

1 DE卷形换能器特点及制备

1.1 DE卷形换能器特点

DE卷形换能器对比普通单轴拉伸DE换能器有2个明显特点：①纯剪切模式的拉伸方式。②自身即可实现预拉伸。

DE换能器的发电原理基于可变电容原理，主要过程为[20]：在发电单元的工作过程中，需要给其提供一个外力拉伸。在弹性体发电单元上下表面加电压，电极加载电荷。当外力拉伸DE膜时，面积增大，由于体积不变，DE膜厚度变小，电容增大，两端电压减少；移除外力后，由于DE材料内部的弹性应力，使得DE材料恢复到之前的状态，面积减小，厚度变大，电容减小，两端电压增大，施加的外力机械能转换为电能。其中的外力拉伸模式主要有单轴拉伸、双轴拉伸以及纯剪切。

单轴拉伸，即只在一个方向上施加作用力，如图1a所示，只有X轴方向受到拉力。

双轴拉伸，即DE膜在两个不同的方向进行互相垂直的拉伸，如图1b所示，DE膜在X轴与Y轴方向上受到拉力。

纯剪切[21]，按照纯剪切定义，弹性体在变形过程中主应变的方向不随变形的递进而转动，而其它拉伸形式中，主应变方向会随着变形的递进而转动。这种变形模式如图1c所示，约束弹性体的X轴方向变形后，在Y轴方向施加拉力，实现纯剪切模式的拉伸。

依据纯剪切拉伸模式的定义，DE卷形换能器的径向方向由固定块固定DE发电单元，限制DE发电单元的径向变形，在轴向方向施加压力实现变形。因此，DE卷形换能器具有纯剪切拉伸模式这一特点。

另外，DE卷形换能器另一特点就是能够实现自身预拉伸。DE卷形换能器的发电单元是DE膜结合弹簧一起制作的，弹簧会将DE膜拉伸到一定长度，实现DE膜的预拉伸。

图1 3种拉伸方式Fig.1 Three kinds of stretching methods

1.2 DE卷形换能器设计

DE卷形换能器的DE膜采用3M公司的VHB4910丙烯酸膜，丙烯酸膜是DE膜材料的一种。电极材料使用导电膏DS- 001。设计的DE卷形换能器机械结构如图2所示，使用电动推杆实现DE膜的拉伸，其具体实现方式为：将2个固定块通过导杆并固定在弹簧上，将DE膜固定在固定块上，其中一端的固定块与滑块相连，实现拉伸。DE膜黏在固定块上，在拉伸时，DE膜的径向无形变，由此构成纯剪切模式。电动推杆通过连接杆与滑块相连，使用电动推杆实现DE膜的拉伸与收缩。

图2 DE卷形换能器模型示意图Fig.2 Schematic diagram of DE roll transducer model1.电动推杆 2.连接杆 3.导杆 4.滑块 5.直线轴承 6.DE膜 7.弹簧 8.固定块 9.底座

图3 DE卷形换能器发电单元示意图Fig.3 Schematic diagram of generating unit of DE roll transducer

2 DE卷形换能器建模

2.1 力学模型

首先，建立DE卷形换能器的力学模型，图3为DE卷形换能器的发电单元示意图，在Z轴方向施加拉力FZ。

假设DE膜体积不变；DE膜上涂覆的电极材料是连续均匀的，厚度为零，不会增加DE膜的厚度；DE膜变形后的半径为B，长度为Z，厚度为H；DE卷形换能器发电单元初始长度为z0，固定膜的固定块半径为ri，膜的初始厚度为h；λB、λH、λZ分别表示DE膜在径向、厚度、轴向的拉伸率。则有

(1)

如图2所示，DE膜是固定在固定块上的，因此其在径向方向是没有拉伸变形的，即λB=1，根据之前假设的DE膜体积不变，则有λHλZ=1，即

(2)

Neo- Hooken模型是一种描述超弹性体的应力应变关系的理论模型，其应变能函数为

(3)

其中

μ=Y/3

式中W——应变能

λ1、λ2、λ3——介电弹性体3个方向上的相对拉伸变形

μ——剪切模量Y——弹性模量

Z方向上的应变能可表示为

(4)

由于DE膜为不可压缩材料(体积不变)，其主应力σ′i可表示为

(5)

式中p——静水压力，主要由动力学边界条件决定

在Z轴方向上的主应力可表示为

(6)

弹簧与DE膜相连可以等效为2个弹簧和1个阻尼器，其等效模型如图4所示。根据牛顿第二定律对Z轴方向进行受力分析，得

(7)

式中k1——弹簧的弹性系数

k2——DE膜等效的弹性系数

dv——等效的阻尼系数

图4 DE卷形换能器等效模型Fig.4 Equivalent model of DE roll transducer

2.2 电学模型

图5 DE卷形换能器外围电路Fig.5 Peripheral circuit of DE roll transducer

外围电路主要由DE卷形换能器、高压偏置电源、负载、储能器件、开关二极管构成，如图5所示。图中，DEG为DE卷形换能器的发电单元，由可变电容表示；U0为外部加的高压偏置电源，为DEG提供偏置电压；Cs为储能电容；D1、D2为开关二极管，目的是限定电流方向，避免回流；R1、R2为负载。

由电工学知识可知

(8)

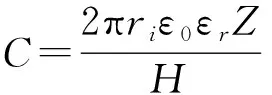
(9)

为了寻找DE卷形换能器的电压变化情况，进行如下运算

(10)

式中u——DE两端电压

进一步化简后有

(11)

(12)

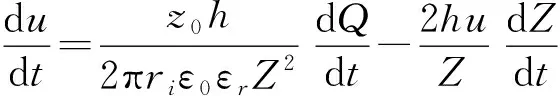
(13)

又

(14)

图6 仿真模型Fig.6 Simulation model

式中t——时间i——回路中的电流

在DE外围设计了电路来求解i(图5)。由图5可得

(15)

将式(14)和式(15)代入式(13)，得

(16)

2.3 机电耦合模型

由式(7)和式(16)共同构成了DE卷形发电机的机电耦合模型为

(17)

3 DE卷形换能器仿真与实验

3.1 DE卷形换能器仿真模型建立及参数设置

根据以上建立的机电耦合模型，使用Matlab/Simulink软件搭建了DE卷形换能器的仿真分析模型，如图6所示。结合实验条件，模型中的具体参数如下：DE膜厚度h=1×10-3m，弹性模量Y=1 MPa，真空介电常数ε0=8.854 187 817×10-12F/m，DE膜介电常数εr=4.7 F/m，电阻R1=8×106Ω，初始电压U0=490 V，DE发电单元质量为0.023 g，固定块周长2πri=0.188 4 m，k1=586 N/m，z0=0.232 m，由于实验测量真实阻尼过小，DE膜的弹性系数也过小，因此dv=0，k2=0。拉力为

(18)

3.2 DE卷形换能器实验平台的建立

根据DE卷形换能器机械结构构建实验平台。DE卷形换能器发电单元如图7a所示，DE卷形换能器实验台如图7b所示。

图7 DE卷形换能器实验装置Fig.7 Experimental device of DE roll transducer1.推杆电动机 2.电容测试仪 3.示波器 4.DE发电单元 5.固定块 6.高压探头 7.电动机控制器 8.电动机电源

3.3 DE卷形换能器发电机理验证及参数优化

(1)DE卷形换能器发电机理验证

根据2.3节建立的DE卷形换能器机电耦合模型及参数进行仿真，其仿真结果如下：

图8为电压随拉伸率的变化曲线，在拉力的作用下 DE卷形换能器被拉长(拉伸率增加)，DE卷形换能器发电单元两端电压逐渐降低，这个过程为 DE卷形换能器的充电过程； 当推杆电动机回程时，DE卷形换能器拉伸率减小，DE卷形换能器发电单元两端电压逐渐升高，即为发电过程。在拉伸与收缩的过程中，DE卷形换能器发电单元两端电压存在高于初始电压的现象，验证了其发电机理。

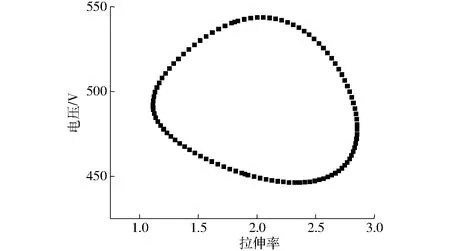
图8 电压与拉伸率的关系曲线Fig.8 Relationship curve between voltage and tensile rate

图9a为仿真时电压随时间的变化曲线，图9b为实验中DE卷形换能器(弹簧k1=586 N/m)的电压随时间的变化曲线，通过对比可以看出其变化趋势是基本一致的。实验曲线的幅值小于仿真曲线的原因：①仿真中忽略了机械损耗、电极内阻损耗、电子元器件损耗等损耗问题。②测量误差。实验曲线与仿真曲线电压变化频率主要是依据拉力的变化周期，由于现实中推杆电动机的拉伸收缩与仿真中拉力的周期不同，因此仿真图与实验图的电压变化频率不同。

图9 电压与时间关系曲线Fig.9 Relationship curves between voltage and time

(2)DE卷形换能器的参数优化

弹簧的弹性系数是影响DE卷形换能器发电性能的一个重要因素。能够依靠自身实现DE膜的预拉伸是DE卷形换能器的一个显著优势，但是如果弹簧的刚度过小，不能够实现DE膜的预拉伸，那么DE卷形换能器中的弹簧就失去了意义，因此，弹簧弹性系数的选择对于DE卷形换能器优化十分重要。

弹簧弹性系数k的选取，与弹簧的制作材料、线径、外径、有效圈数有关，如图10所示，其计算公式为

(19)

其中

D=D1-2d

式中D1——弹簧外径

G——弹簧材料的剪切模量

d——弹簧线径D——弹簧中径

N——弹簧有效圈数

弹簧的材料为钢，其剪切模量G=8×104MPa。

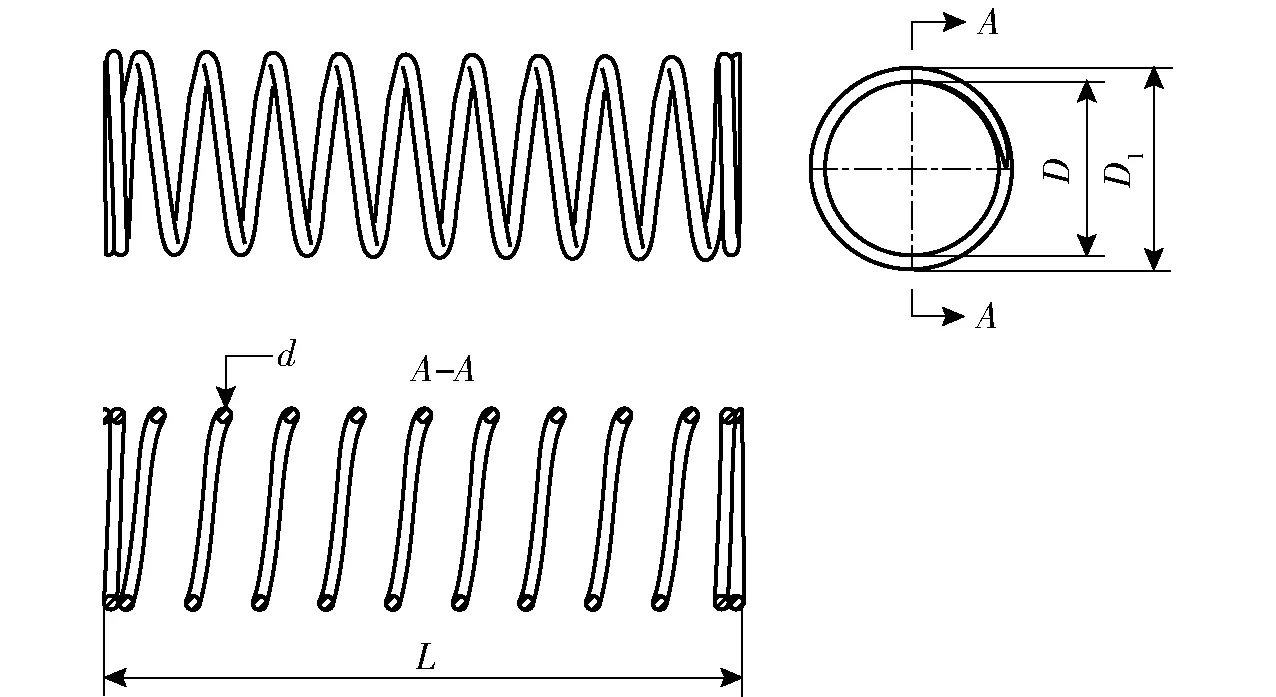
图10 弹簧模型Fig.10 Spring model

本文选取了不同型号的弹簧进行实验，其型号选择如表1所示。

利用不同k的弹簧分别制作了DE卷形换能器的发电单元，其具体参数如表2所示。弹簧初试长度为30 cm，压缩后可达到的最小长度为6 cm，DE膜的初始长度为15 cm。利用DE卷形换能器进行实验时，其压缩发电行程设置为12 cm，电压升高值的实验结果如表2所示，在测量过程中，发现DE卷形换能器的电容与上升电压都是随着预拉伸长度的增加而增加，即随着弹簧的弹性系数k的增大而增大。当k取值为64.16、133.33、191.71 N/m时，DE卷形换能器的初试长度不足够被压缩12 cm，因此其不满足实验测量要求，未做测量。

表1 弹簧参数Tab.1 Spring parameters

表2 DE卷形换能器发电单元参数Tab.2 Parameters of generating unit of DE roll transducer

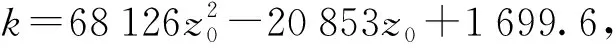
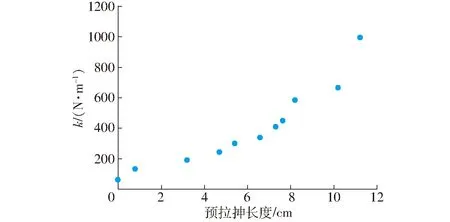
图11 预拉伸长度与k关系Fig.11 Relationship between prestretch length and k

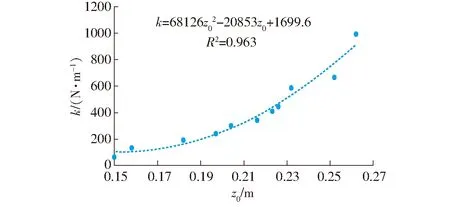
图12 z0 与k的关系曲线Fig.12 Relationship curve between z0 and k

将k值与z0的拟合函数代入仿真模型中，得到k与DE卷形换能器发电单元两端电压的关系，如图13所示，图13a是仿真得出的关系曲线，电压随弹性系数k的增加而增加，一直到弹簧的弹性系数k=1 575.04 N/m时，弹簧可将DE卷形换能器的发电单元弹起到30 cm(与弹簧长度一致)，当k>1 575.04 N/m时，DE卷形换能器的初始长度不再改变，但是压缩发电过程所需的外力会增大，因此，DE卷形换能器在k=1 575.04 N/m时达到最佳发电性能。图13b为实验得出的关系曲线，与仿真曲线的趋势一致，即 DE卷形换能器的发电性能随着弹簧弹性系数的增加而增加，分析仿真与实验关系曲线在最高点时趋势的变化，主要是由于在实验过程中，弹簧在实际的实验过程中，实验台所能驱动的最大刚度的弹簧其弹性系数k=991.57 N/m，因此，在实际实验过程中并没有达到仿真中的最佳k值，依据现有的实验条件，DE卷形换能器的弹性系数k的较优选择为991.57 N/m。

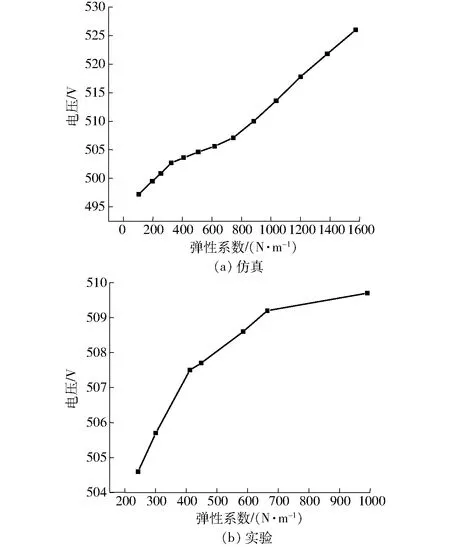
图13 DE电压与弹性系数关系曲线Fig.13 Relationship curve between DE voltage and elastic coefficient

3.4 DE卷形换能器性能测试

性能测试实验是将DE卷形换能器与单轴拉伸的DE膜升高电压进行对比。单轴拉伸实验中使用的DE膜其类型、尺寸以及柔性电极材料都与DE卷形换能器相同，实验中测得其电容为531.2 pF，DE发电单元两端电压上升幅度为11.3 V。将其与弹簧弹性系数为991.57 N/m的DE卷形换能器进行对比，结果如图14所示，DE卷形换能器的发电特性优于单轴拉伸时的发电特性。

图14 DE单轴拉伸与DE卷形换能器发电性能对比Fig.14 Comparison of generation performance of DE uniaxial tension and DE roll transducer

4 结论

(1) DE卷形换能器自身具有预拉伸功能以及纯剪切的拉伸模式，使其发电性能远大于一般单轴拉伸模式的DEG，在同等实验条件下，DE卷形换能器的电容有1.52 nF，端电压达到19.7 V，而单轴拉伸模式的DEG其发电单元的电容仅为531.2 pF，端电压则为11.3 V。

(2) DE卷形换能器仿真分析中，进行参数优化后发现DE卷形换能器弹簧弹性系数的最佳选择为1 575.04 N/m，但实验过程中，由于受实验装置的限制，弹性系数为991.57 N/m时最优。

1 PELRINE R, KORNBLUH R, PEI Q, et al. High-speed electrically actuated elastomers with strain greater than 100% [J]. Science, 2000, 287(5454): 836-839.

2 POTZ M, ARTUSI M, SOLEIMANI M, et al. Rolling dielectric elastomer actuator with bulged cylindrical shape [J]. Smart Materials & Structures, 2010, 19(12): 127001.

3 朱银龙, 张鑫焱, 王华明, 等. 介电型电活性聚合物驱动转动关节控制技术研究[J/OL]. 农业机械学报, 2015，46(7): 333-338.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150747&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2015.07.047.

ZHU Y L, ZHANG X Y, WANG H M, et al. Research on actuation control of dielectric electroactive polymer rotary joint [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 333-338.(in Chinese)

4 GODABA H, LI J, WANG Y, et al. A soft jellyfish robot driven by a dielectric elastomer actuator [J]. IEEE Robotics & Automation Letters, 2016, 1(2): 624-631.

5 LU Z, SHRESTHA M, LAU G K. Electrically tunable and broader-band sound absorption by using micro-perforated dielectric elastomer actuator [J]. Applied Physics Letters, 2017, 110(18): e1501595-5242.

6 CURTIS M, IHLEFELD, QU Z H. A dielectric electroactive polymer generator-actuator model: modeling, identification and dynamic simulation [C]∥ Proceedings of SPIE,2008, 6927: 1-11.

7 CHIBA S, WAKI M, KOMBLUH R, et al. Extending applications of dielectric elastomer artificial muscle [C]∥ Proceedings of SPIE, 2007,6524: 652424.1-652424.5.

8 LALLART M, COTTINET P J, GUYOMAR D, et al. Electrostrictive polymers for mechanical energy harvesting[J]. SPIE, 2004, 5385(5): 523-535.

9 KANG G, KIM K S, KIM S. Analysis of the efficiency of a dielectric elastomer generator for energy harvesting [J]. Review of Scientific Instruments, 2011, 82(4): 692715.

10 KALTSEIS R, KEPLINGER C, BAUMGARTNER R, et al. Method for measuring energy generation and efficiency of dielectric elastomer generators [J]. Applied Physics Letters, 2011, 99(16): 162904.1-162904.3.

11 ZHOU J, JIANG L, KHAYAT R E. Investigation on the performance of a viscoelastic dielectric elastomer membrane generator [J]. Soft Matter, 2015, 11(15): 2983-2992.

12 BINH P C, NAM D N C, AHN K K. Design and modeling of an innovative wave energy converter using dielectric electro-active polymers generator [J]. International Journal of Precision Engineering & Manufacturing, 2015, 16(8): 1833-1843.

13 WANG H, WANG C, YUAN T. On the energy conversion and efficiency of a dielectric electroactive polymer generator [J]. Applied Physics Letters, 2012, 101(3): 071101.

14 GOUDAR V, REN Z, BROCHU P, et al. Optimizing the output of a human-powered energy harvesting eystem with miniaturization and integrated control[J]. Sensors Journal IEEE, 2014, 14(7): 2084-2091.

15 VERTECHY R, FONTANA M, PAPINI G P R, et al. In-tank tests of a dielectric elastomer generator for wave energy harvesting [C]∥ Proceedings of SPIE, 2014,9056: 90561G1-90561G11.

16 JEANMISTRAL C, VUCONG T, SYLYESTRE A. Energy scavenging strain absorber: application to kinetic dielectric elastomer generator [C]∥ Proceedings of SPIE, 2014,9056: 90561H1-90561H8.

17 KORNBLUH R D, PELRINE R, PRAHLAD H, et al. From boots to buoys: promises and challenges of dielectric elastomer energy harvesting[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2011, 7976(10): 67-93.

18 CHIBA S, WAKI M, WADA T, et al. Consistent ocean wave energy harvesting using electroactive polymer (dielectric elastomer) artificial muscle generators [J]. Applied Energy, 2013, 104(2): 497-502.

19 曹建波, 葛彩军, 鄂世举,等. 基于Neo- Hooken的介电弹性体单轴拉伸发电特性研究[J/OL]. 农业机械学报, 2016, 47(3): 389-394.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160355&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2016.03.055.

CAO Jianbo, GE Caijun, E Shiju, et al. Power generating characteristics of uniaxial tensile for DEG based on Neo- Hooken model [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3):389-394.(in Chinese)

20 鄂世举，朱喜林，高春甫．介电弹性体发电的基本原理及在分布式发电中的应用[J]．现代制造工程, 2009, 23(9)：141-145．

E Shiju, ZHU Xilin, GAO Chunfu. The basicmechanism of dielectric elastomer generator and its application in distributed power generation [J]. Modern Manufacturing Engineering, 2009, 23(9): 141-145.(in Chinese)

21 李博. 介电弹性材料驱动器的力电耦合机理及稳定性研究[D]. 西安：西安交通大学, 2012.

LI Bo. Electromechanical coupling and stability in dielectric elastomer actuator[D].Xi’an: Xi’an Jiaotong University,2012.(in Chinese)