Nerve conduction models in myelinated and unmyelinated nerves based on three-dimensional electrostatic interaction

Tetsuya Akaishi

1 Department of Neurology, Tohoku University Graduate School of Medicine, Sendai, Japan

2 Department of Neurology, Yonezawa National Hospital, Yonezawa, Japan

Introduction

In the nervous system, conduction of the signals has been described as a form of electrical current with membrane potential change. To explain the propagation of membrane action potential in the axon, the conventional cable theory assumed closed electric circuits that fulfill Ohm’s law and Kirchhoff’s law, spreading inside and outside the axoplasm(Hodgkin and Huxley, 1952; Koch, 1984).

These conventional theories can theoretically explain the physiological phenomena of the nerve conduction and can also predict some potential‐related properties like the anod‐al break (Guttman and Hachmeister, 1972; Daly et al., 2015).The following equation is the famous “cable equation”, with which we can describe and simulate the membrane potential at the location of “x” at a specific time of “t” (Vm(x,t) ) by us‐ing the space constant of “λ” and the time constant of “τm”.

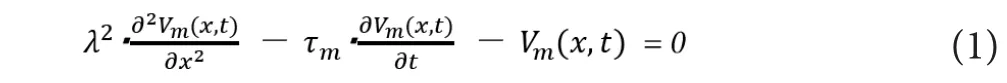
Though these conventional theories are certainly sophisticated, there are some issues in their premises that have not been fully addressed yet. First, whether we can really sup‐pose closed electric circuits in the actual site of the nervous system or not from the viewpoint of electrostatic molecular interactions has not been fully discussed yet. Another issue is that we cannot explain the different relationships between axonal diameter and conduction velocity in unmyelinated and myelinated nerves. The cable theory explains the two‐di‐mensional propagation of membrane action potential across the axonal membrane, but whether we can also apply the

＊Correspondence to:Tetsuya Akaishi, M.D., Ph.D.,t-akaishi@med.tohoku.ac.jp.

orcid:0000-0001-6728-4966(Tetsuya Akaishi)

doi:10.4103/1673-5374.232460

Accepted:2018-03-19model to saltatory conduction in myelinated nerves or not is not clear. The conduction velocity is proportional to the axonal diameter in myelinated nerves, but it is proportion‐al to the square root of diameter in unmyelinated nerves.However, until now, there is no mathematical model that can explain the saltatory conduction.

From before, the membrane action potential has known to be accompanied by some mechanical changes in axonal parameters like radius, length, pressure, and heat (El Hady and Machta, 2015). Based on this fact, some axonal structures like neurofilament, lipid bilayer, or axoplasm have been supposed to play some roles in nerve conduction (Shrivas‐tava and Schneider, 2014). Though the exact mechanism of saltatory conduction is still unknown, these recent findings imply that we are better to consider not only the two‐dimensional signal propagation along the axonal membrane but also three‐dimensional mechanical signal conduction as the nature of nerve conduction.

In this report, a new model of nerve conduction from a viewpoint of molecular interaction between electrical‐ly‐charged particles in the axoplasm will be presented. Different from the conventional theories that focused to the two‐dimensional propagation of membrane potential, the new conduction model focuses to the three‐dimensional ionic/molecular interaction within electrolytes like axo‐plasm. With this new conductive model, we do not need to assume closed electric circuits in the intracellular or extracellular fluid and we can just focus on the density and distribution of voltage‐gated sodium (NaV) channels in the membrane.

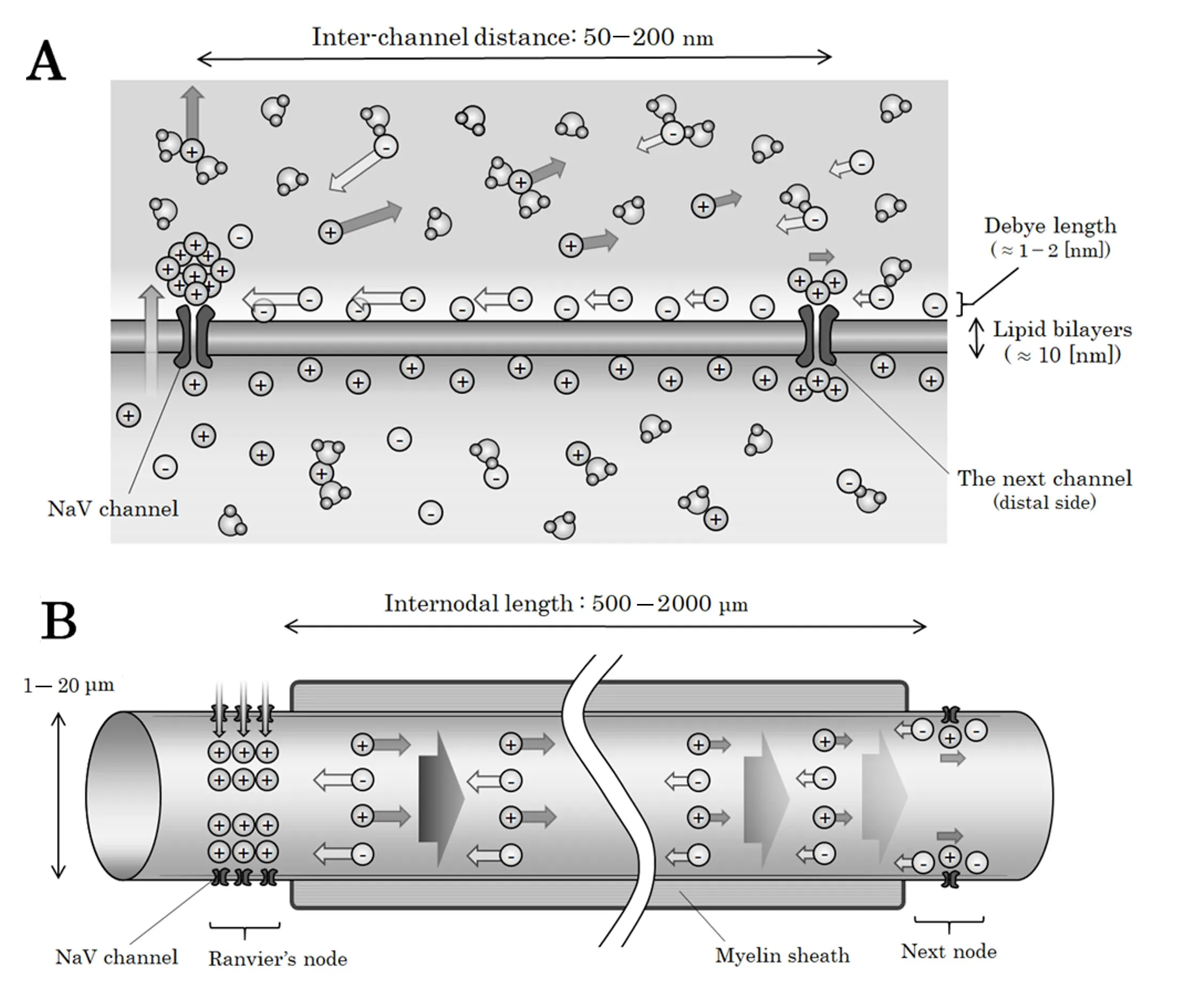
Figure 1 Illustrations of the neural structures in unmyelinated and myelinated nerves.

Actual Scale of the Structures in Nervous System

he illustrations of neuronal structures with approximate measures in unmyelinated nerves and in myelinated nerves are shown in Figure 1. To be noted, the absolute scale of the figures in unmyelinated nerves (Figure 1A) and in my‐elinated nerves (Figure 1B) are totally different. As can be seen, the distance between two adjacent NaV channels in unmyelinated nerves is less than one‐thousandth of that between two adjacent Ranvier’s nodes in myelinated nerves.This simple scale‐related issue would result in different conductive pattern in unmyelinated and myelinated nerves;the forefront of the signal in unmyelinated nerves would proceed along the internal surface of the axonal membrane but the forefront of saltatory conduction in myelinated nerves would proceed across the whole cross‐section of the axoplasm. Previously, this scale‐related issue between un‐myelinated nerves and myelinated nerves has not been fully considered and all of the nerve conduction has been ex‐plained from the viewpoint of two‐dimensional propagation of membrane action potential across the axonal membrane.In this report, for the nerve conduction in unmyelinated nerves, we consider a micro‐scale three‐dimensional prop‐agation of an electrostatic compressional wave with hemispheric surface along the internal surface of axonal membrane. For the saltatory conduction in myelinated nerves,we consider a macro‐scale one‐directional internodal prop‐agation of an electrostatic compressional wave with plane surface across the whole cross‐section of the axoplasm.

Electrostatic Mechanism of NaV Channel Activation

When a NaV channel is activated, a specific rate of sodium ions in flux will be triggered and a mass of positive electric charges will appear in the intracellular fluid. The extracellular space where the transferred cations originally located will be instantly supplied by other numerous cations existing in the extracellular fluid. As a result, we can assume a situation that a mass of positive electric charges has gradually appeared on the internal surface of the NaV channel. This newly appeared positive‐ly‐charged mass would exert electrostatic force for both intra‐cellular and extracellular electric charges. Here, NaV channel is known to be negatively‐charged and attracting cations on its surface (Hille et al., 1975; Dani, 1986; Yin et al., 2013). Then,we can estimate that the distribution of electric charges are different between the internal and external surfaces of the axonal membrane in unmyelinated nerves (Figure 1A) and in Ranvi‐er’s nodes in myelinated nerves (Figure 1B).

From before, voltage‐gated ion channels have been regarded to open by responding to the decrease in potential difference between the internal and external sides of the membrane. To produce such difference in the potential gradient across the membrane, actual drift of some electri‐cally‐charged substances (i.e., intracellular ions, membrane protein, or membrane itself) as a chain reaction is required.To create such changes in the potential gradient across the membrane at the next NaV channel, the conducted signal needs to alter the horizontal (i.e., parallel to the membrane)potential gradient across the internal surface of the nextchannel. The separation of cations on the internal surface of the NaV channel depends on the horizontal component of the transmitted electrostatic force, which would be transmit‐ted directly or as an electrostatic compressional wave within the axoplasm. Because the transmitted electrostatic force originally results from the sodium ion in flux at the preceded depolarized NaV channels in unmyelinated nerves and from the influx at the preceded depolarized Ranvier’s nodes in myelinated nerves, the distance between NaV channels and the amount of NaV channels in each Ranvier’s node would be important. However, both of these variables have not been fully taken into considerations in the conventional the‐ories. In the new conduction model, these variables will be incorporated as the essential components of the nerve con‐duction. The list of the abbreviations of the variables used in this mathematical conduction model and their theoretical roles are listed in Table 1 in the alphabetical order.

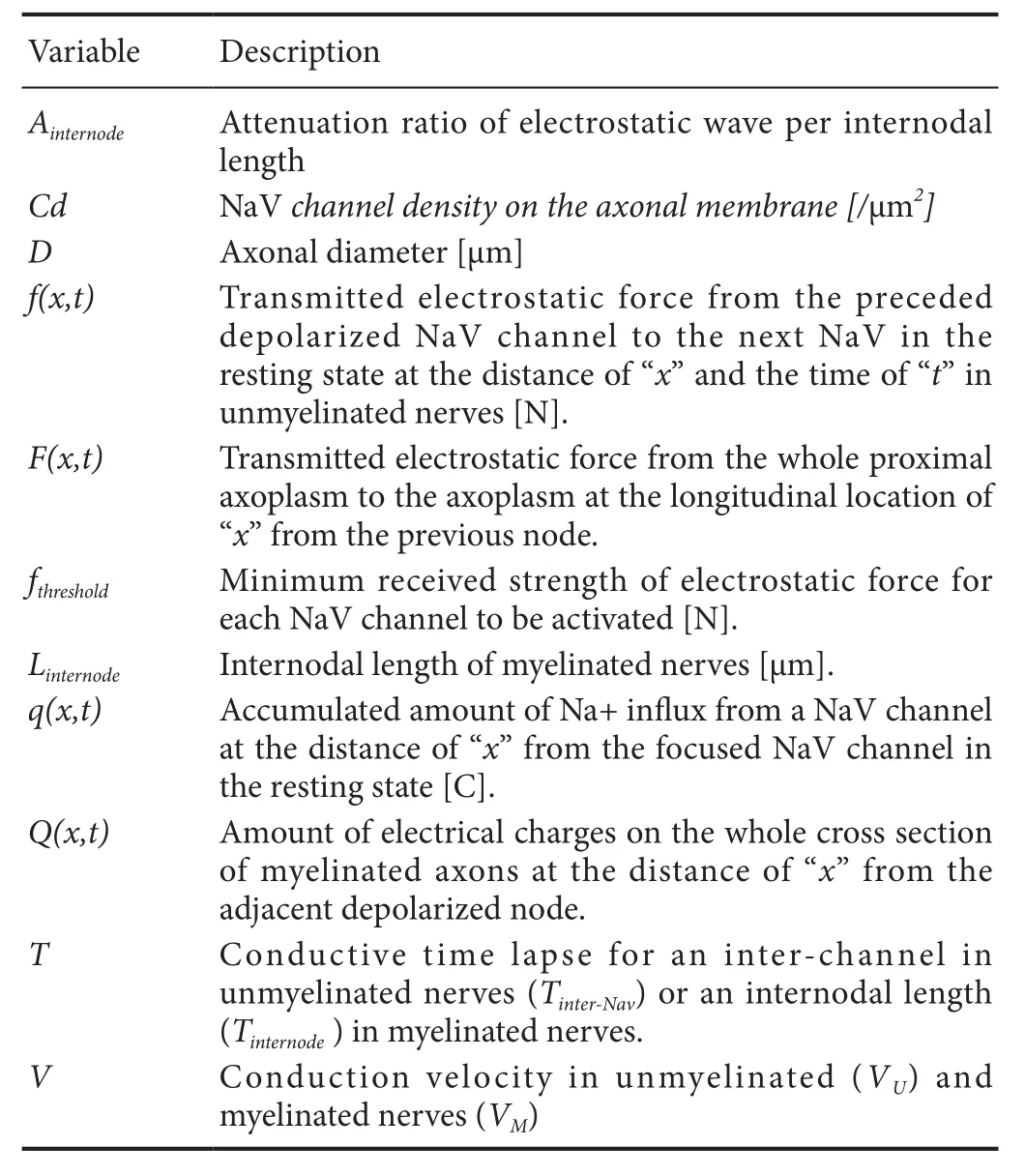
Table 1 List of variables used in the conduction model

Distribution of the Product of Two Variables with Normal Distribution

Before starting to build up a mathematical conduction mod‐el, we need to consider about the distribution of the product of two variables each of which shows normal distribution.Here, we prepare two independent random variables of “A”and “B”, which independently follows normal distributions ofN(μA,σA) andN(μB,σB), respectively. Here, we describe their probability densities withfA(a) andfB(b).

The distribution of the productA·Bis known not to follow the normal distribution; thus, its mode is not equal toA·B.On the other hand, the expected value ofA·B(i.e.,IE(A·B))fulfills the following equations, becausefAB(a,b) is equal to the product offA(a) andfB(b) .

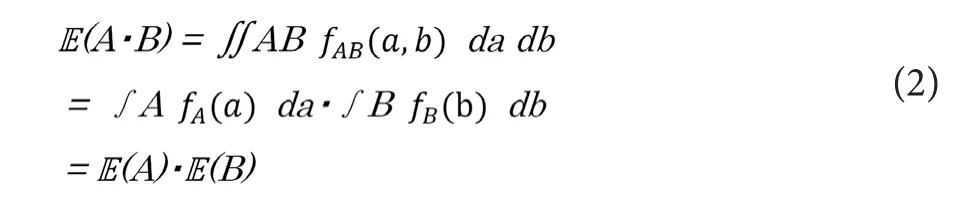
Thus, if the sample sizes of “A” and “B” are enough large, the mean of the productA·Bcan be expected to match the value of the productμA ·μB.

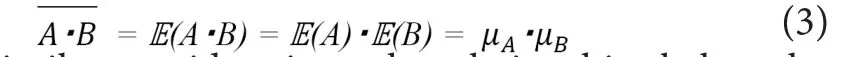
Based on similar considerations, the relationships below also holds.

These facts will be applied to the following proportional ex‐pressions as their rationales.

Mathematical Model for Three-Dimensional Electrostatic Interaction within Electrolyte Solution

The strength of electrostatic force between two spots with electrical charges can be described as below.

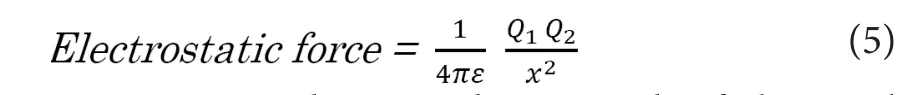
In this equation,Q1andQ2are the strength of electrical charges [C], “x” is the distance between the two spots [m],and “ε” is the permittivity of the medium [N·m2/C2]. Next,we apply the above‐mentioned equation to the electrostatic force working in electrolyte solution like intracellular fluid or axoplasm. If we suppose that a mass of electrical charges appeared in an electrically‐charged medium, the charged mass would exert electrostatic force to the surrounding charges. The strength of electrostatic force that the ion particles at the distance of “x” [m] from the center of the mass would receive from the inner solution can be described as below (Akaishi, 2018).

In this equation,F(x,t)stands for the strength of electrostatic force [N] that the electrical charges with the distance of “x”[m] from the charged mass at the time of “t” receive from the inner solution andQ(x,t)stands for the amount of positive electric charges [C] at the location of “x” [m] from the mass at the time of “t”. Because this equation holds in all the infinitesimal time, the following equation would also hold.

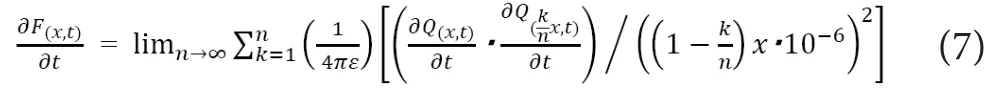
These concepts hold no matter of the dimension of the electrostatic force propagation (e.g., one‐dimensional propagation with plane surface or three‐dimensional propagation with hemispheric surface) as shown in Figure 2. No matter of unmyelinated nerves or myelinated nerves, the most important regulators for nerve conduction would be the distance from the depolarized NaV channels to those in resting state and the Na+in flowing rate in the depolarized segments.

More detailed figure explaining the mathematical basis of three‐dimensional electrostatic interaction in myelinated nerves is shown in Figure 3. This figure shows that the strength of the electric field in the axoplasm at the longitudinal distance of “X” created by the change of electrical charges in thek‐th previous portion (E(k–th proximal→x,t)[N/C])would be proportional to the total amount of NaV channels in the adjacent depolarized Ranvier’s node. Thus, in a my‐elinated axon with a specificDandLinternode, we can say that the strength of the electric field in the axoplasm at a specific distance of “X” from the previous node would be proportional to the amount of NaV channel in one Ranvier’s node.

Figure 2 Overview of the saltatory conduction model based on electrostatic interaction.

Figure 3 Mathematical basis of the electrostatic compressional wave in myelinated nerves.

Conduction Model in Unmyelinated Nerves

Propagation of electrostatic compressional wave along the internal surface of axonal membrane in unmyelinated axons

In unmyelinated nerves, we can ideally assume that the NaV channels in the axonal membrane would be almost homo‐geneously dispersed across the membrane. Certainly, the transmitted depolarized “excitation” segment on the axonal membrane would have variable ranges depending on the channel density (Cd) and conduction velocity (VU) in unmy‐elinated nerves. As shown below, the estimated longitudinal (i.e., direction from the proximal to distal of the axon)width would be more than 100 times larger than the average distance of adjacent NaV channels (dinterchannel), if we assume the conduction velocity of unmyelinated nerves (VU) to be around 1.0 m/s and the channel density (Cd) to be around 100 channels/μm2.

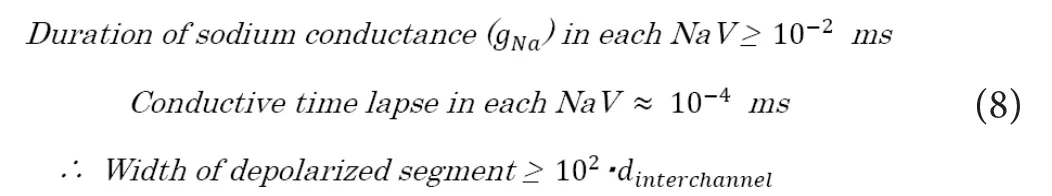
Though the depolarized axonal segment in one signal con‐duction has a variable width with multiple NaV channels in the longitudinal direction, the most important factor that regulates the conduction velocity would be the average distance between each adjacent NaV channels in the membrane, because the proceeding of the depolarized segment to the distal side is resulted from the electrostatic interaction between the depolarized segment and the adjacent next NaV channel on the minimally distal side (Figure 1A). Here, we define the electrostatic force from the depolarized “excitation” segment of axonal membrane to the closest adjacent NaV channel on the distal side as “f(depolarized→next NaV)”, which can be described as below.

Here, based on (5),∂f(k-th preceded NaV→next NaV)/∂tcan be described as below by using the NaV channel density of “Cd” and the amount of positive charges at the longitudinal location of “X”as “q(X)”.

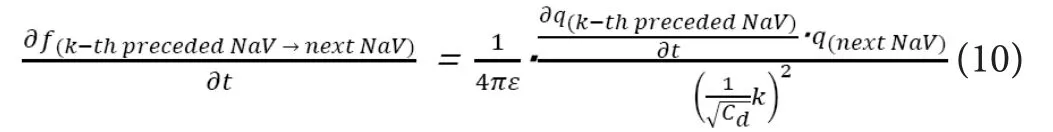
Here, the section of∂q(k–th preceded NaV)/∂twould be almost constant in the depolarized segment, especially in NaV channels with smaller values of “k” (i.e., closer to the next NaV). Thus,based on (9) and (10), the following relation would hold.

Strictly speaking,∂q(k–th preceded NaV)/∂tcannot be regarded as constant in the later phase of depolarization state and other electrical states; thus, the upper limit range of “k” in the above relationship would not ∞, but around 100–1000.However, the section of (1/k2) can be negligible with enough large values of “k”, and the segment of∑k=1(1/k2) can still be regarded as constant. Thus, the following relationship would be derived.

Then, the time lapse of the depolarized “excitation” segment in the axonal membrane to activate the closest adjacent NaV channel on the distal side (T(depolarized→next Nav)) can fulfill the following relationship.

Because the longitudinal numbers of NaV channels on a specific length of axon is proportional to, the conduction velocity of unmyelinated nerves (VU) would fulfill the following relationship, which is compatible with the established fact.

Derived simultaneous equations in unmyelinated nerves

Based on the theories described above, the nerve conduction in unmyelinated nerves can be described with the following simultaneous equations.

In the equation (16),fthresholdstands for the minimum strength of received electrostatic force for each NaV channel to be activated. Here, though not described in detail in this report, the theoretical relationship betweenCdand axonal diameter (D) can be theoretically supposed to be linear as shown in the previous reports (Akaishi, 2017, 2018). This is based on the previous reports describing that the amount of axonal transport to be proportional to the cross‐sectional area (S) of the axon (Wujek et al., 1986). If we can suppose this assumption, combined with the relation (14), the fol‐lowing relationship can be deduced, which is compatible with the already known fact.

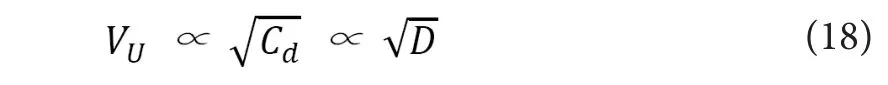
Conduction Model in Myelinated Nerves

Propagation of electrostatic compressional wave on the whole cross-section of internodal axoplasm

Different from the propagation of nerve signal in unmyelinated nerves, signal conduction based on electrostatic inter‐actions would proceed evenly on the whole cross‐section of the internodal axoplasm in myelinated nerves. This is mostly because the internodal length between adjacent Ranvier’s nodes (300–2000 μm) is much larger than the axonal diameter (1–20 μm) in myelinated nerves (Akaishi, 2018).

In this section, for convenience, we focus to one internod‐al segment between two adjacent Ranvier’s nodes and regard the focused axoplasmic segment as a closed physical system,in which the total of mechanical energy is ideally preserved.

Significance of internodal length in the saltatory conduction

When we consider about the saltatory conduction in myelin‐ated nerves, we need to define how to treat the internodal length (Linternode). We need to decide whether to treatLinternodeas constant irrespective ofDor as a covariate related toD. To prove that we should not regard to be constant and that the correlation between andDis important, we will tentatively assumeLinternodeto be constant irrespective ofDand will show the deduced conclusion is in conflict with the observed facts.

Here, we defineF(x, t)as the electrostatic force working from the whole proximal axoplasm to the ions on the whole axonal cross section at the longitudinal location of “x” (i.e.,distance from the proximally adjacent depolarized node) at the time of “t”. If we tentatively regardLinternodeto be constant at “X”, the following relationship would hold based on (7).

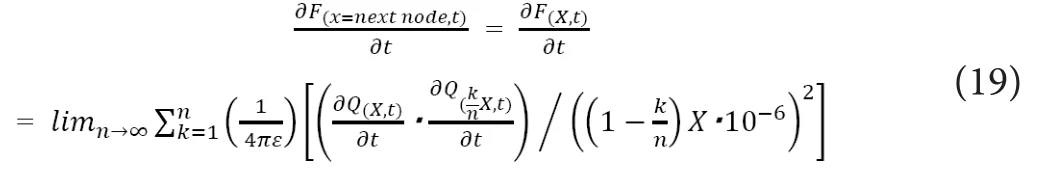
From the viewpoint of ionic drift based on electrostatic interactions and ionic diffusion based on concentration gradient, the partial derivative of∂Q(x, t)would be proportional to the change rate of ionic amount at the infinitesimally proximal location at the preceding infinitesimal time (Δt). If we can ignore the longitudinal (i.e., from proximal to distal)mechanical energy loss from friction with the internal surface of axonal membrane, the following equations hold by using the proportionality constant of “C” (0 ＜C＜ 1), which is specific to the width ofx/nand the type of the medium.

Because we are now regardingLinternodeas being constant at“X”, these relations would hold irrelevant of the axonal diameter and the infinitesimal time of “Δt” can be regarded as a medium‐specific constant. Combining (19) with (20), the following relationships can be derived.

Thus, if we regardLinternodeto be constant at “X”, the follow‐ing relations can be derived by applying the mathematical induction.

BecauseLinternodeis tentatively supposed to be constant at “X”here, the transmitted force to the next node would be always proportional to the total amount of NaV channels in each node, irrespective of the axonal diameter.

Here, based on the above mentioned previous report (Wujek et al., 1986), the total amount of expressed NaV channels in the full length of an axon would be proportional to the area of axonal cross section. Then, if we regardLinternodeto be constant irrespective of axonal diameter (D), the total amount of NaV channels in one Ranvier’s node would fulfill the fol‐lowing relation.

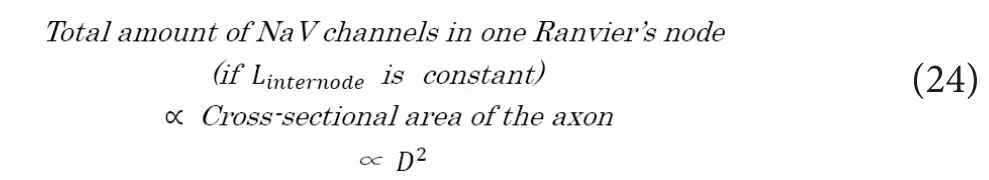
Thus, the transmitted electrostatic force to each of the NaV channels on the next node (f(previous node→next node, t)), which can be described as below, would wrongly come to be constant irrespective ofD.

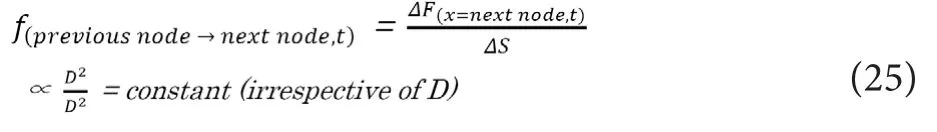
If this relationship is true, the conduction velocity in my‐elinated nerves would wrongly be always constant irrespective ofD, which is incompatible with the already established knowledge of “VM∝D”. This result means that we must not assumeLinternodeto be constant irrespective ofD. As a conclusion of this section, the linear relationship betweenDandLinternodewould be the key factor realizing the faster saltatory conduction in larger myelinated axons.

Simultaneous Equations for the Saltatory Conduction in Myelinated Nerves

Based on the theories described above, we need to incorpo‐rate the variable ofLinternodeinto the simultaneous equations.By usingAinternodeas the attenuation ratio of the electrostatic force per each internodal length, the conduction model for the saltatory conduction in myelinated nerves can be described with the following simultaneous equations.In the equation (26),F(x=previous node, t)would be proportional to the total amount of NaV channel in the previous Ranvier’s node. In the equation (27),ΔSstands for infinitesimally small cross‐sectional area of an axon at Ranvier’s nodes.

Relationship between Internodal Length and Conduction Velocity in Myelinated Nerves

Based on the results of the previous section that the inter‐nodal length, rather than axonal diameter, would be essential for the accelerated saltatory conduction, in this section,we consider how the observed linear relationship betweenLinternodeandDmay affect the transmitted electrostatic com‐pressional wave in the axoplasm.

First, based on the two below‐mentioned linear relations,the required conductive time lapse in each internode be‐tween two Ranvier’s nodes (Tinternode) is always constant irrespective of axonal diameter (Akaishi, 2018).

Also, based on this fact, if we consider about one Ranvier’s node which has just turned to depolarization state, the electrical states of the proximal and distal Ranvier’s nodes in each signal conduction are to be automatically determined irrespective of the axonal diameter.

BecauseTinternodeis always constant irrespective ofD,f(previ-ous node→ next node, t)would be also constant irrespective ofD. Now,f(previous node→ next node, t)can be described as below.

On the premise of “Linternode∝D”, the total amount of NaV channels in each Ranvier’s node would fulfill the following relation.

Based on (30) and (31), the following relation holds.

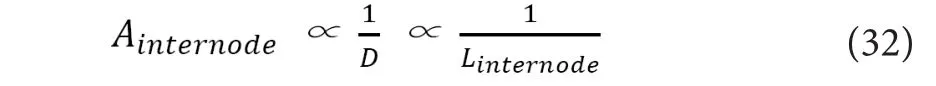
As conclusions of this section, based on the already established knowledge, the time lapse per each internode (Tinternode)would be always constant, irrespective of the axonal diame‐ter. Combined with the theoretical premise of “Cd∝D”, the attenuation ratio of the electrostatic force per each internode(Ainternode) was suggested to be proportional to the internodal length (Linternode).

Supposed Electrostatic Compressional Wave in Signal Integration and Neural Backpropagation

In the previous sections, we considered electrostatic com‐pressional wave within the axoplasm in myelinated nerves.Though we did not suppose such conductive mechanism in unmyelinated nerves because the forefront of the signal con‐duction would proceed along the internal surface of axonal membrane, the total number of NaV channels in a specific length of axon is estimated to be larger in unmyelinated nerves than in myelinated nerves. More specifically, though the length of Ranvier’s node is about one‐thousandth of that in the internodal segment (Linternode), the channel density (Cd)in Ranvier’s nodes of myelinated nerves is no more than 100 times higher than that in unmyelinated nerves (Arancib‐ia‐Carcamo et al., 2017). Thus, we can estimate that, though the forefront of conducted signals would proceed along the internal surface of axon, electrostatic compressional wave it‐self seems to exist even in unmyelinated axons and dendrites.

The dendrites are known to be normally unmyelinated and widely express voltage‐gated potassium channels (Kv channel) on them, not NaV channels as seen in the axons(Johnston et al., 2000, 2003). Though the type of the volt‐age‐gated ion channels are different between dendrites and axons, the basic theoretical mechanism of signal conduction can be regarded as almost similar between them. Thus, in this section, we also apply the above‐described conductive model in unmyelinated nerves to the dendritic signal conduction and assume a delayed electrostatic compressional wave on the cross‐section of the dendrites.

The density of NaV channels and Kv channels in the membrane of neural cell body has known to be significantly low(≈ 1.0 channel/μm2), and a previous study reported that an attempt to produce action potential in the soma failed even with a normal proper stimulating procedure (Safronov et al., 1997; Wolff et al., 1998). This fact suggests that we are better to think about the signal conduction, integration, and back‐propagation in the neuronal cell body to spread not on the two‐dimensional internal surface of the membrane of cell body but across the cytoplasm with three‐dimensional extent.

We do not have much information about the signal con‐duction, integration, and back‐propagation in the neural cell body yet. Three‐dimensional propagation of electrostatic compressional wave not only in the axon but also in the neural cell body may be a promising candidate of the element realizing the above‐mentioned neural physiological functions.

Limitations

The biggest problem of this new model at present is that the theoretical relationship of “Cd∝D” has not been experimentally confirmed yet. This will be evaluated by applying the immunofluorescent staining for the ion channels and measuring the luminescence and the axonal diameter. Another limitation is that we do not fully consider about the possible factors that can affect the conduction velocity in this model.Some of such factors are the full length of axon, extracellular electrolytic concentrations, and temperature. The last limitation is that, though we only considered intracellular ions to be the carrier of electric charges in this model, there are some other possible carriers like membrane protein, cell surface sugar chain, and the membrane itself. Whether we can really ignore these factors as electric carriers in nerve conduction or not is still to be verified.

Conclusions

In this review, the newly introduced conductive model based on intracellular electrostatic interactions was described.Based on this model, in unmyelinated nerves, the channel density in the membrane (Cd) was suggested to be important to realize the faster conduction. In myelinated nerves, the internodal length (Linternode) and the total amount of NaV channels in each Ranvier’s node were suggested to be important for the faster conduction. The proposed three‐dimensional propagation of electrostatic compressional wave within the intracellular fluid may be associated with the physiological mechanisms of signal integration and back‐propagation in the neural cell body.

Acknowledgments:The author thanks Dr. Toshiyuki Takahashi (Yonezawa National Hospital, Japan) for his professional advices related to this study.

Author contributions:The author confirms being the sole contributor of this work.

Conflicts of interest:The author declares that there is no conflict of interest.Financial support:None.

Copyright license agreement:The Copyright License Agreement has been signed by all authors before publication.

Plagiarism check:Checked twice by iThenticate.

Peer review:Externally peer reviewed.

Open access statement:This is an open access journal, and articles are distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License, which allows others to remix, tweak, and build upon the work non-commercially, as long as appropriate credit is given and the new creations are licensed under the identical terms.

Open peer review report:

Reviewer:Jianxun Ding, Chang Chun Institute of Applied Chemistry Chinese Academy of Sciences, China.

Comments to author:This manuscript reported a new theoretical model of nerve conduction, which could explain different conductive patterns in unmyelinated and myelinated nerves. This mathematical conductive model based on electrostatic compressional wave and focused on more valuable variables,i.e., density and distribution of voltage-gated sodium (NaV) channels in the membrane. In general, it is a convictive manuscript, which introduces the mathematical conductive model that may be able to explain the physiological phenomena occurring in the nervous system.

Akaishi T (2017) New theoretical model of nerve conduction in unmyelinated nerves. Front Physiol 8:798.

Akaishi T (2018) Saltatory conduction as an electrostatic compressional wave in the axoplasm. Tohoku J Exp Med 244:151‐161.

Arancibia‐Carcamo IL, Ford MC, Cossell L, Ishida K, Tohyama K, Attwell D(2017) Node of Ranvier length as a potential regulator of myelinated axon conduction speed. Elife 6:e23329.

Daly AC, Gavaghan DJ, Holmes C, Cooper J (2015) Hodgkin‐Huxley revisit‐ed: reparametrization and identifiability analysis of the classic action potential model with approximate Bayesian methods. R Soc Open Sci 2:150499.

Dani JA (1986) Ion‐channel entrances influence permeation. Net charge, size,shape, and binding considerations. Biophys J 49:607‐618.

El Hady A, Machta BB (2015) Mechanical surface waves accompany action potential propagation. Nat Commun 6:6697.

Guttman R, Hachmeister L (1972) Anode break excitation in space‐clamped squid axons. Biophys J 12:552‐563.

Hille B, Woodhull AM, Shapiro BI (1975) Negative surface charge near so‐dium channels of nerve: divalent ions, monovalent ions, and pH. Philos Trans R Soc Lond B Biol Sci 270:301‐318.

Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117:500‐544.

Johnston D, Hoffman DA, Magee JC, Poolos NP, Watanabe S, Colbert CM,Migliore M (2000) Dendritic potassium channels in hippocampal pyramidal neurons. J Physiol 525 Pt 1:75‐81.

Johnston D, Christie BR, Frick A, Gray R, Hoffman DA, Schexnayder LK,Watanabe S, Yuan LL (2003) Active dendrites, potassium channels and synaptic plasticity. Philos Trans R Soc Lond B Biol Sci 358:667‐674.

Koch C (1984) Cable theory in neurons with active, linearized membranes.Biol Cybern 50:15‐33.

Safronov BV, Wolff M, Vogel W (1997) Functional distribution of three types of Na+channel on soma and processes of dorsal horn neurones of rat spinal cord. J Physiol 503:371‐385.

Shrivastava S, Schneider MF (2014) Evidence for two‐dimensional solitary sound waves in a lipid controlled interface and its implications for biological signalling. J R Soc Interface 11:20140098.

Wolff M, Vogel W, Safronov BV (1998) Uneven distribution of K+channels in soma, axon and dendrites of rat spinal neurones: functional role of the soma in generation of action potentials. J Physiol 509:767‐776.

Wujek JR, Lasek RJ, Gambetti P (1986) The amount of slow axonal transport is proportional to the radial dimensions of the axon. J Neurocytol 15:75‐83.

Yin Y, Sun W, Li Z, Zhang B, Cui H, Deng L, Xie P, Xiang J, Zou J (2013) Effects of combining methylprednisolone with rolipram on functional recovery in adult rats following spinal cord injury. Neurochem Int 62:903‐912.