浅谈汽车ABS滑移率的模糊滑模控制

朱永

广州市高级技工学校 广东省广州市 510440

1 引言

汽车防抱死制动系统（ABS）可以在极限情况下维持车轮和整体车辆的稳定性，是保证汽车安全的一个重要系统。汽车ABS系统的核心是控制系统，ABS系统的制动性能受控制效果的影响非常巨大，其中目前最常用的控制方法是基于滑移率的控制方法。在进行ABS系统设计的时候，常常会提到最佳滑移率的概念。所谓的最佳滑移率，就是指汽车轮胎附着系数最大时的滑移率，汽车的轮胎一直处于最佳滑移率是最理想的状态，但是汽车在实际行驶的时候会受到非常多的因素的影响，所以汽车制动系统也是一个非线性的不确定的复杂系统，而传统的控制方法基本都是建立在线性系统的基础上，所以控制效果不好。目前国内外的很多学者纷纷提出很多新型的控制理论。

目前国际上有非常多的控制方法来实现对汽车ABS系统滑移率的控制。下面我们就来详细分析一下国际上常用的滑移率控制方法。逻辑门限值控制方法是一种最简单的控制方法，但是在测定门限值的时候要进行大量的试验才能准确测量，并且使用该控制方法会增加系统的调试难度，而且控制准确度也不是最高的，使用逻辑门限制控制方法开发的系统适用性较差，仅仅在小范围内具有很强的适用性。PID控制方法也是一种简单的控制犯法，当使用最佳滑移率作为参考滑移率的时候，PID控制系统的控制效果非常好，但是在实际的汽车行驶过程中，路面情况是会不断发生变化的，随之而来的是汽车最佳滑移率的变化，但是参考滑移率是不能随意变动的，这就使得PID控制系统在实际运用的过程中控制效果较差。而且，PID控制系统在调整参数的时候流程非常复杂，难度也比较大，所以PID控制系统在ABS系统中也很少使用。模糊控制方法对参数变化的适应性较强，外界干扰对系统的影响也比较小，但是和其他控制系统相比，模糊控制方法的响应速度要慢于其他控制系统，而且模糊控制系统质量的好坏是与设计者的能力直接挂钩的，这就导致不同的模糊控制系统之间存在很大的性能差异。而且，模糊控制系统对路面特征的识别效果较差，这导致模糊控制系统不能在路况变化之后及时的变更系统的参考滑移率。滑模变结构控制系统也是当前国际上一个非常流行的控制方法，和其他的控制方法相比，滑模变结构控制系统的响应速度更快，但是对滑模参数的依赖程度较高。而且滑模变结构控制系统缺乏相应的理论支持，控制效果的好坏受设计者影响非常严重，与模糊控制系统相同，滑模变结构控制系统也不能识别路面特征。而自适应系统可以实现对路面特征的识别，而且可以根据路面状况的变化而进行自动调整，不断的修正参考滑移率，控制效果要远远好于上述的几种控制系统。

在实际设计的使用，并不一定要采用单一的控制算法，可以充分利用不同控制算法的特点，将几种控制算法结合起来。目前国际上已经有很多专家学者开始将几种控制方法结合起来。比如模糊PID控制算法、自适应模糊控制算法、模糊滑块控制算法，这些都是目前国际上非常流行的结合控制方法。这些结合控制算法都有其独特的优点和缺点，本人在经过研究之后，提出一种新的组合控制算法——ABS自适应模糊滑模控制算法，这种算法继承了自适应控制算法的有点，在不同的路面特征下可以及时的修正参考滑移率，同时该组合控制算法还继承了滑模控制算法的特点，整个控制系统的响应速度得到了极大的提高，利用模糊控制算法实现对系统参数的自动调整，提高制动系统的实用性和安全性。

2 控制系统原理

2.1 轮胎的纵向附着系数——滑移率特性

在经过实验研究之后，专家学者发现纵向附着系数和滑移率之间的关系并不是一种简单的线性关系而是一种复杂的非线性关系，在滑移率增加到某一数值之前，轮胎的纵向附着系数也会逐渐增加直到达到峰值。但是如果在纵向附着系数达到峰值之后滑移率继续增加，纵向附着系数反而会不断下降，如果将纵向附着系数和滑移率之家你的关系画成函数曲线，我们就可以非常显著的发现，图像有一个最高点，而最高点所对应的滑移率我们称之为最佳滑移率。汽车ABS系统的原理就是轮胎附着系数与滑移率的关系而设计的。那么汽车ABS系统是怎么来控制滑移率的呢？一般情况下，汽车ABS系统都是通过控制轮胎与地面之间的制动压力来实现对滑移率的控制的，如果增加轮胎和路面之间的纵向附着力，汽车的制动压力就会大幅度的提高，从而就能够非常快速的实现制动，增加车辆行驶的安全性。

不同的实验会得到不同的纵向附着系数和滑移率之间的函数关系模型，当前最流行的公式是魔术公式模型：

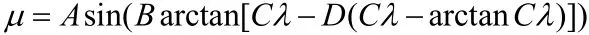
其中式中的ABCD全部为待定系数，可以通过试验测量。下面给出几组具有代表性的路面参数数据。在干燥的沥青路面上，A=0.85，B=2.4，C=4.5，D=0.9。最佳滑移率为0.2。在松砾石路面上，A=0.45，B=2.4，C=5.0，D=0.9。最佳滑移率的值为0.155。

2.2 单轮汽车运动模型

为了减少问题研究的难度，所以在研究的时候，我们忽略掉次要因素，将模型进行适当的简化突出主要问题，现在我们做出下列假设：首先，我们假定汽车的转向角输入为0，同时忽略掉汽车的垂直运动和倾侧现象，只考虑汽车的纵向的直线运动，而且我们也不考虑汽车的侧向运动和横摆运动。同时我们也不再考虑转向系统对整个汽车的影响，并且假定汽车的自重和载荷均匀分布与四个轮胎之上。最后我们假定轮胎在制动过程中不发生变形，忽略因为制动而导致的汽车质心位置的变化。我们假定汽车行驶的路面是理想路面，不存在坡度和坑洼。

在进行了上述假设之后，这时我们可以将汽车的运动简化为单轮汽车运动模型，纵向轮胎受到纵向摩擦力F的作用，产生纵向加速度v，车轮中心出轮胎受到制动力矩T和纵向摩擦力F产生的力矩作用以角速度ω，纵向摩擦力的力臂为轮胎的半径R。根据牛顿力学定律，我们可以建立如下的物理学模型：

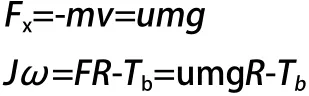
2.3 制动系统模型

汽车的制动系统实现制动的最根本的方式就是将制动压力转化为制动力矩，传动机构和制动器是制动系统的两个重要组成部分，本文所涉及的传动机构是液压传动系统。液压传动系统和其他传动系统相比延迟比较大，所以在进行研究分析的时候，我们可以将液压传动系统可以简化为一个带迟滞的一阶惯性环节，其传递函数为：

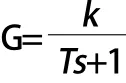
式中的参数T=0.01，K=100。

制动系统的制动器可以将液压传动系统提供的压力变成制动力矩以此来实现制动效果，在理想的状态下，制动器制动力矩为：

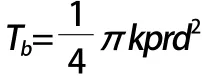
3 控制器设计

3.1 滑模控制器设计

滑模控制器根据滑移率λ跟踪最佳的差e来进行制动压力调解，这样就可以降低跟踪误差。通过计算我们可以得出，最佳滑移率是通过自适应调节器来确定的，而滑模参数是通过模糊逻辑调解器来确定的。

3.2 自适应调节器设计

本组合控制算法可以充分利用获得的滑移率λ和纵向附着系数μ来对最佳滑移率的数值进行实时的调控，当汽车行驶在不同的路面上时，最佳滑移率就可以随时的进行变化，以此来确保系统的安全性与稳定性，自适应调节的原理是基于轮胎纵向附着系数和滑移率的关系曲线特性来建立的，由于最佳滑移率对应的是纵向附着系数的峰值位置，所以峰值两侧的曲线斜率为一正一负。

3.3 模糊逻辑调节器设计

在滑模控制器设计的时候，滑模参数的设定并没有什么科学的理论依据，一般都是通过多次实验的方法来进行确定，这就使得滑模参数的设定非常的复杂繁琐，而且得出的参数准确度也不是很高。而模糊逻辑调节器自身具有很强的自适应性，所以我们可以利用模糊逻辑调节器自动的调整滑模参数。

我们将模糊逻辑调节器的输入变量选择为误差e和误差变化率Δe，输出变量选择为滑模参数k1、k2的变化率Δk1、Δk2。输入和输出的语言变量的隶属度函数都设置为钟型函数，变量等级设置为5级，根据输入变量和输出变量之间的定性关系，我们就可以建立一个模糊规则表。

4 仿真

在汽车ABS系统设计完成之后，还要对其进行验证。

我们首先进行单一路面情况下的仿真，仿真中选择干沥青路面。在完成仿真之后发现，当选择不同的自适应滑模参数，那么仿真结果也不同。在多次试验之后，我们可以发现，控制效果最好的滑模参数为k1=500，k2=0.01，使用这个参数进行仿真之后得到的制动距离为24.3006米，制动时间为2.417秒。附着系数的利用率为0.9337。为了实现与自适应滑模控制系统的比较，我们将自适应模糊滑模控制的滑模参数也设置为k1=500，k2=0.01。滑模参数的变化是通过模糊逻辑调节器输出乘上输出比例系数来得到的，当我们选择不同的比例系数的时候，仿真的结果也不完全相同。在多次比较之后，我们选择输出Δk1的比例系数为96，输出Δk2的比例系数为0.01，仿真试验得到的制动距离为24.2993米，制动时间为2.417秒。为了验证所提出的控制算法对不同路面情况的适应性和控制效果，我们分别在不同的路面状况下对自适应滑模控制器和自适应模糊滑模控制器进行仿真，我们假设，汽车现在平坦干燥的沥青路面上行驶一定距离，然后进入光滑冰路面。在沥青路面上时，最佳滑移率λd=0.2，最大纵向附着系数μ=0.85。在光滑的冰面上，最佳滑移率λd=0.155，最大纵向附着系数μ=0.1。

和单一路面仿真相似的是，不同路面情况下自适应滑模参数的不同也会极大的影响仿真的结果，通过多次试验，我们发现最后选择效果最好的滑模参数k1=350，k2=0.01。由此得到的制动距离为87.1181米，制动时间为13.051秒，附着系数利用率为0.9990。与上面的做法相同，我们仍然将不同路面情况下的自适应模糊滑模控制系统的滑模参数初始值设定为k1=350，k2=0.01，滑模参数的变化也是通过模糊逻辑调节器输出乘上输出比例系数而得到的。通过实验我们可以发现，当比例系数不同的时候，得到仿真结果也不相同。通过多次试验我们可以发现，当我们选择输出Δk1=78，输出Δk2=0.01时，仿真的制动距离为87.0883米，制动时间为13.049秒，附着系数的利用率为0.9991。

本文所提出的基于自适应调节器和模糊逻辑调节器的自适应模糊滑模控制算法从根本上来说是切实可行的，而且只需要很短的时间就可以快速的达到稳定，稳定系数较大，所以稳定性较强，响应也非常的迅速，和其他的控制算法相比，利用自适应模糊滑模控制器的汽车ABS纵向附着系数的利用率更大，制动距离也更加短，更加可以保护司机的乘客的安全。

5 结语

本文提出了一种由自适应调节器和模糊逻辑调节器结合而产生的自适应模糊滑模控制算法，当前国际上非常流行的几种组合控制算法他们都不具备识别路面的能力，缺乏自适应能力，而且都具有或多或少的缺点，而本文所提及的自适应模糊滑模控制算法的制动时间较短，具有优异的制动效果，自适应调节器可以获得的轮胎附着系数和滑移率信息对最佳滑移率进行修正，使得系统的参考滑移率不再是一个固定的值，而是可以随着实际情况的不同而实时的发生变化的，增强了系统的适应能力，在不同的路面下，ABS系统都可以迅速的调整最佳滑移率的数值，使得汽车的制动系统始终保持在一个高效的状态，具有非常强的制动效果。滑模控制器可以快速调节制动压力，所以本控制系统可以极大的减少制动时间和汽车的制动距离，大幅度增加汽车的安全性能。模糊逻辑调节器可以根据系统滑移率的变化对滑模参数进行自动调整，使得系统存在一定的自适应性。本文所提出的自适应模糊滑模控制算法综合了自适应控制算法、模糊控制算法、滑模控制算法三种算法各自的优点和缺点，取长补短，弥补了目前我们所使用的几种控制算法的不足和缺点，极大的提高了ABS系统的性能和效率。汽车的ABS系统直接关系到了汽车驾驶员和乘客的人身安全，是汽车安全性能的保障，而控制算法又是ABS系统的核心部分，所以选择合适的控制算法是ABS系统设计的核心部分。设计人员在进行ABS系统设计的时候，必须要综合的全面的考虑问题，可以采用本文所提到的自适应模糊滑模控制算法来进行ABS系统的设计，增加汽车的安全性能。