基于改进粒子群优化BP_Adaboost神经网络的PM2.5浓度预测
李 晓 理, 梅 建 想, 张 山
( 1.北京工业大学 信息学部, 北京 100124;2.计算智能与智能系统北京市重点实验室, 北京 100124;3.数字社区教育部工程研究中心, 北京 100124 )
0 引 言
随着工业化程度不断加大,废气、废渣排放增加,大气污染愈发严重,尤其是颗粒物质(PM)污染,这一问题已引起国家相关部门高度关注.颗粒物质不仅会影响居民生活、出行,破坏生态系统,而且跟人类健康密切相关.在过去几十年间,研究表明,人口每日死亡率增长和各种疾病症状(如哮喘、慢性支气管炎、肺功能下降等)与大气中颗粒物质浓度有显著关系.因此,许多业界人士对如何预测大气污染物中PM2.5浓度开展了相应研究,为居民生活、出行提供决策.最初,统计学方法被用于预测空气污染物,Kumar等用自回归整合移动平均模型预测印度德里郊区每日臭氧、一氧化碳、氮氧化物平均浓度[1];Elbayoumi等结合大气污染物变量和气象条件,利用多元线性回归模型预测当地室外PM2.5浓度随着时间和季节的变化趋势[2].Ishak等利用多元线性回归、模糊系统和广义可加模型研究突尼斯当地历史时刻PM2.5浓度对未来空气质量预测的影响[3].同时,Nieto等通过建立多元自适应回归样条预测模型,分析出了西班牙奥维耶多当地气象分布特征[4].虽然这些回归模型被应用于大气污染预测,但是复杂地形、气象条件、污染物等多种因素共同影响,导致预测模型呈现出高度非线性,增加了PM2.5浓度预测难度.因此,传统回归模型在用于大气预测中,往往难以满足允许精度,预测性能欠佳.
大量研究表明,相比于传统统计学方法,神经网络具有良好的非线性逼近、自组织和自学习能力,无须确定输入和输出之间函数关系,只需通过对数据样本进行训练,利用训练好的网络来对输入数据进行预测[5],可以有效解决建模难题,因此其被广泛应用于大气污染预测.孙宝磊等采用MIV方法筛出主要因子,建立BP神经模型预测昆明地区日均污染物浓度[6];针对芬兰赫尔辛基城区,Kukkonen等建立多种神经网络模型预测PM2.5小时平均质量浓度[7];同样地,石灵芝等建立BP神经网络模型预测湖南长沙火车站PM10小时平均质量浓度[8].Elangasinghe等用BP神经网络结合k-means聚类算法[9],建立了一个基于监测站气象条件和PM2.5、PM10浓度预测模型,能够有效预测新西兰南侧岛屿空气主要污染指数.由此看出,BP神经网络模型具有较好预测性能,已引起人们广泛关注.但是,BP是一类弱预测器,存在过拟合和容易收敛于局部极小点问题.因此,模型预测精度有待进一步提高.
为此本文将BP神经网络和Adaboost算法结合,提出一种基于BP_Adaboost神经网络[10-11]的PM2.5浓度预测模型,建模时考虑影响PM2.5浓度的多种因素,并用灰色关联分析选取影响PM2.5浓度的主要因子作为神经网络输入变量;此外,运用改进粒子群算法来优化神经网络权重和阈值,以有效避免陷入局部最优解;最后以北京市海淀区万柳监测站和朝阳区北京工业大学监测点的实时数据为例,验证模型预测性能.
1 改进粒子群优化BP_Adaboost神经网络模型建立
1.1 灰色关联分析
灰色系统理论认为,含有已知信息或不确定性信息的系统,从表面上看,数据可能是随机的、杂乱无章的,但是其仍然是有界和有序的,数据集内会呈现一定规律.正如对天气预报系统而言,大气中PM2.5浓度受多种因素共同影响,各因素间相互关系无法定量分析,还会在一定范围内波动,属于动态变化的.因此,可借助灰色关联分析方法鉴别各因素之间发展趋势的相互依赖程度,找出各因素对PM2.5浓度的影响程度[12-13],其计算步骤如下:
步骤1建立原始数据矩阵xi
xi=(xi(1)xi(2) …xi(k))
(1)
式中:xi(k)为第i个因素在第k时刻的原始数据;i=1,2,…,7,k=1,2,…,n,n为原始数据长度.
步骤2计算初始化变换矩阵x′i
x′i=(xi(1)/xi(1)xi(2)/xi(1) …
xi(k)/xi(1))=
(x′i(1)x′i(2) …x′i(k))
(2)
步骤3计算差序列Δoi(k)
Δoi(k)=xi(k)-x′i(k)
(3)
步骤4计算关联系数ξoi(k)和灰色关联度γoi
(4)
其中φ为分辨系数,其作用在于提高关联系数间的差异显著性,φ∈(0,1),经过多次反复试验可得,本文中φ取为0.6.
(5)
在灰色关联分析过程中,以PM10、NO2、CO、O3、SO2的浓度和温度、相对湿度为变量,分别得出北京市海淀区万柳监测站和朝阳区北京工业大学监测点数据关联系数依次为ξo1=(0.982 6 0.872 1 0.745 8 0.722 5 0.898 2 0.927 1
0.931 8),ξo2=(0.972 9 0.884 5 0.752 7 0.710 9 0.872 6 0.942 8 0.930 1).
从上述结果可以看出,PM10浓度、温度、相对湿度、NO2浓度和SO2浓度关联系数较大,因此,提取出这5个变量作为影响PM2.5浓度的主要因子.
1.2 BP_Adaboost神经网络
1.2.1 核心思想 在绝大多数集成学习算法通过构造越来越复杂的预测器来提高预测精度时,Adaboost却追求将最简单的弱预测器组合得到强预测器.在训练子预测器的方法上,Adaboost提供了重要启示:打破已有样本分布,重新采样使预测器更多地关注难学习的样本.在算法使用上,仅需要指定迭代次数,不需要任何先验知识,一切运行过程中的参数由算法自适应地调整,因此被评价为最接近“拿来即用”的算法[14].
Adaboost算法是组合多个弱预测器输出生成强预测器[15].首先,从样本空间中抽取m组作为训练数据,每组训练数据的权重均初始化为1/m.然后,分别训练弱预测器,迭代运行T次后,每组训练数据权重依据预测结果进行动态调整,若预测误差未能达到允许值将增大其权重,进一步加强学习.经过反复迭代后,弱预测器将得到一个预测函数序列f1,f2,…,fT,若预测结果越好其权重越大,反复迭代T次,通过弱预测函数加权得出强预测函数h(x),实现数据预测.
1.2.2 算法流程与步骤 基于BP_Adaboost模型的PM2.5浓度预测算法流程图如图1所示,算法步骤如下.
步骤1数据获取和网络初始化.选取m组训练数据,赋予训练数据权重分布为Dt(i)=1/m,依据样本输入和输出维数确定网络结构,网络初始权重和阈值由改进粒子群算法优化获得.

图1 BP_Adaboost算法结构Fig.1 The structure of BP_Adaboost algorithm
步骤2弱预测器.训练第t个弱预测器时得到预测序列g(t)的预测误差和
(6)
式中:y为期望值.
步骤3计算预测序列权重.依据预测误差et计算权重at:
(7)
步骤4测试数据权重调整.根据权重at调整下一轮训练样本权重,如下:
(8)
式中:Bt是归一化因子,y为期望值.
步骤5强预测函数.经过T次迭代,由T组弱预测器函数f(gt,at)生成强预测器函数h(x).
(9)
1.3 改进粒子群优化BP_Adaboost神经网络
1.3.1 改进粒子群算法 粒子群(particle swarm optimization,PSO)算法是一种模拟生物机制的全局随机搜索算法,其通过搜索当前最优值来找到全局最优值[16].首先,对粒子进行初始化,接着经过数次迭代寻找最优解,在此过程中粒子速度和位置更新公式如下:
vis=ωvis(t+1)+c1r1s(t)(pis-xis(t))+
c2r2s(t)(pgs(t)-xgs(t))
(10)
xis(t+1)=xis(t)+vis(t+1)
(11)
(12)
式中:pis是第i个粒子所经历过最好位置,pgs是粒子群中最好位置;学习因子c1和c2分别为调节粒子飞向自身最好位置和全局最好位置方向的步长,取c1=1.496 2,c2=1.496 2;r1s和r2s为服从[0,1]均匀分布伪随机数;vis是粒子速度,其值变化范围为-10~10;ω为惯性权重,用来控制前一速度对当前速度的影响,ω越大,越有利于全局搜索,而ω越小则越有利于精确局部搜索,寻找到最优解,因此,采用变化惯性权重可以有效避免陷入局部最优解.为了更好地平衡算法全局和局部搜索能力,避免算法早熟和在全局最优解附近产生振荡现象,本文采用权重线性递减PSO算法.其中,ω随算法迭代次数变化公式为式(12),t和tmax分别表示当前和最大迭代步数,设定tmax=100,ωmax=0.9,ωmin=0.4,ω在不断迭代过程中线性递减,该算法能够寻找到最优解且具有很好收敛性.由式(10)、(11)和(12)可知,惯性权重、学习因子和随机数共同决定粒子飞行速度,需要调整参数较少,避免只依赖经验对ω进行调节.
将粒子群算法全局搜索能力与神经网络学习算法相结合,既可解决盲目寻优问题,又能避免发生局部收敛情况.在运用PSO算法时,将粒子群初始位置向量设为BP_Adaboost神经网络权重和阈值,然后用改进粒子群算法在整个粒子群中搜索最优位置,使均方误差最小化,直至满足算法停止条件.此时,将最优位置向量赋给BP_Adaboost 神经网络权重和阈值,再训练网络,直至算法停止.相比于随机初始化神经网络权重和阈值而言,经优化后的神经网络不易陷入局部极小点,从而能够提高算法性能.
1.3.2 基于改进粒子群BP_Adaboost神经网络在搜索空间中,粒子群按事先设定飞行速度,在不断搜索和寻优过程中,其根据个体和群体飞行经验进行动态更新,其算法流程图如图2所示,其算法步骤如下:

图2 PSO算法流程图Fig.2 The flow chart of PSO algorithm
步骤1初始化PSO算法相关参数.
步骤2计算每个粒子适应度值.
步骤3比较每个粒子当前和历史最好位置的适应度值,若较好,则把它视为当前最好位置.
步骤4比较每个粒子当前和全局最好位置的适应度值,若较好,则把它视为当前全局最好位置.
步骤5根据式(10)、(11)和(12)对速度和位置进行更新.
步骤6如果满足终止条件,则输出最优个体,并赋给BP_Adaboost神经网络,否则返回到步骤2.
步骤7训练已构建好的BP_Adaboost神经网络,进行仿真实验.
2 PM2.5实验数据分析和预测
北京作为中国首都,近些年来,由于人流量较大,工业化程度不断加大以及周边城市的影响,市内空气污染严重.在北京市内,有35个监测站,包括23个环境评估点和1个郊区控制点,负责监测城市空气质量.同时,6个边界地区监测点用来反映周边城市对北京市环境的影响.在二环、三环以及四环主干道路口设置5个交通监测点,用来反映交通流量信息.本文选取了北京市海淀区万柳监测站和朝阳区北京工业大学监测点数据作为实验研究对象,该数据分别来自于城市空气项目[17]和空气质量传感网络监测仪,后者性能指标、外观和数据界面如图3所示.大量研究表明,PM2.5主要化学成分很复杂,含有碳物质(有机碳、元素碳)、硫酸盐、硝酸盐、铵盐等[18],而且各物质在大气中还存在复杂物理和化学变化,因此,可以得出PM2.5浓度与大气污染物变量和气象条件相关.

(a) 性能指标
由于影响PM2.5浓度因素很多,如气象条件、大气污染物浓度、交通流量、工业排放废气和废物等,考虑到监测站数据样本的重要性和有效性,选取北京市海淀区万柳监测站(2014-11-01~2014-11-25)和朝阳区北京工业大学监测点(2017-07-07~2017-08-06)每小时监测数据进行实验,如图4和5所示.此外,为了研究两个监测站在1 d内6种大气污染物浓度变化所呈现规律,以万柳监测站(2014-11-08)和北京工业大学监测点(2017-07-20)数据为例进行分析,如图6和7所示.
从图4和5可以看出,PM2.5浓度与PM10浓度呈现出一致变化,具有很强相关性,而与温度和相对湿度有着负相关的变化趋势.此外,在夏季期间,多种污染物浓度较低,尤其是NO2和SO2浓度较低,空气质量较好,而在冬季多种污染物浓度相对较高.在不同季节,PM2.5浓度差异性显著,一般地,冬季PM2.5浓度相对较高,主要来源于燃煤量急剧增加,导致大量颗粒性物质被排放到大气中,而且在冬季温度和相对湿度较低,大气结构稳定,导致污染物累积易形成污染事件.
从图6和7可以看出,1 d当中各污染物浓度呈现两头高中间低的变化趋势,即凌晨和夜间污染物浓度较高,其他时间段相对较低,这与温度和相对湿度有着直接关系.在凌晨和夜间,温度和相对湿度较低,不利于各种污染物扩散,导致污染物不断累积.但是,随着温度升高和相对湿度变大,污染物消散加速,污染物浓度会降低.

图4 万柳监测站2014-11-01~2014-11-25数据Fig.4 The data from November 1 to November 25, 2014 at Wanliu station

图5 北京工业大学监测点2017-07-07~ 2017-08-06数据Fig.5 The data from July 7 to August 6, 2017 at Beijing University of Technology point

图6 万柳监测站2014-11-08数据Fig.6 The data on November 8, 2014 at Wanliu station
此外,上述这些数据是每间隔1 h监测的,为了消除各数据之间量纲差异性,对于该神经网络的训练数据和测试数据,皆采用最大最小法进行归一化:
(13)
式中:xmin为数据序列最小值,xmax为数据序列最大值,xnorm∈[0,1].
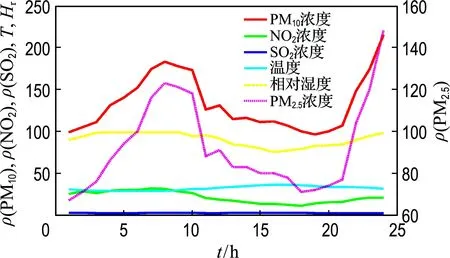
图7 北京工业大学监测点2017-07-20数据Fig.7 The data on July 20, 2017 at Beijing University of Technology point
在本次实验中,由灰色关联分析结果知,下一个小时PM2.5浓度与当前时刻PM10浓度、温度、相对湿度、NO2浓度和SO2浓度关联系数较大,故选取当前时刻PM10浓度、NO2浓度、SO2浓度、温度和相对湿度作为该神经网络输入变量,大气中下一个小时PM2.5浓度作为输出变量.在实验过程中,选取万柳监测站(2014-11-01~2014-11-25)总共512个冬季数据样本和北京工业大学监测点(2017-07-07~2017-08-06)总共744个夏季数据样本,再分别从中随机选取400个和600个数据样本训练神经网络,其网络训练误差曲线如图8(c)、9(c)所示,确定其权重和阈值,使其收敛,并能够满足在不同季节数据样本下预测大气中PM2.5浓度的要求.经过多次重复实验,选取训练误差最小,最终确定BP神经网络结构为5-6-1,BP_Adaboost神经网络由10个BP神经网络模型训练生成.待神经网络训练完成后,为了验证其预测性能,再分别用剩余112个和144个数据样本来测试网络,从而实现提前1 h预测大气中PM2.5浓度的功能.

(a) 模型预测结果

(a) 模型预测结果
3 结果和讨论
3.1 性能指标
在本文中,选取3种不同算法进行对比,为了衡量其预测性能,定义3种统计指标用来评估,依次为均方根误差(erms)、平均绝对百分比误差(emap)、相关系数(R2),其计算公式如下:
(14)

(15)
(16)
式中:Oi为PM2.5浓度在第i时刻实际值,Yi为同一时刻模型预测值,

Y-
为模型预测输出平均值.erms反映模型预测输出值稳定性,emap反映模型预测输出值偏离PM2.5浓度实际值程度,两者值皆越小,性能越好;R2反映PM2.5浓度实际值与模型预测输出值相关联程度,其值越接近1,性能越好.
3.2 预测结果
针对万柳监测站和北京工业大学监测点每小时监测数据,运用改进粒子群优化BP_Adaboost神经网络(MPSO-BP_Adaboost)建模进行仿真实验,其预测结果如图8和9所示.此外,将本文中所采用预测模型和BP_Adaboost、BP、广义回归神经网络(GRNN)3种预测模型进行对比,其性能指标见表1和2.
从图8和9可以看出,针对万柳监测站和北京工业大学监测点,采用改进粒子群优化BP_Adaboost神经网络建模来对大气中未来1 h PM2.5浓度进行预测,预测输出值和期望输出值基本相吻合,能够达到高精度预测的效果.在某些时间点预测时,可能由于外部环境突变、一些人为因素和神经网络自身性能等原因,存在预测误差,但是,网络输出相对误差只是在一个较小范围内波动,在大气预测应用方面可以接受,因此,BP_Adaboost 神经网络能够很好实现预测功能.

表1 万柳监测站4种预测模型性能指标对比
表2 北京工业大学监测点4种预测模型性能指标对比
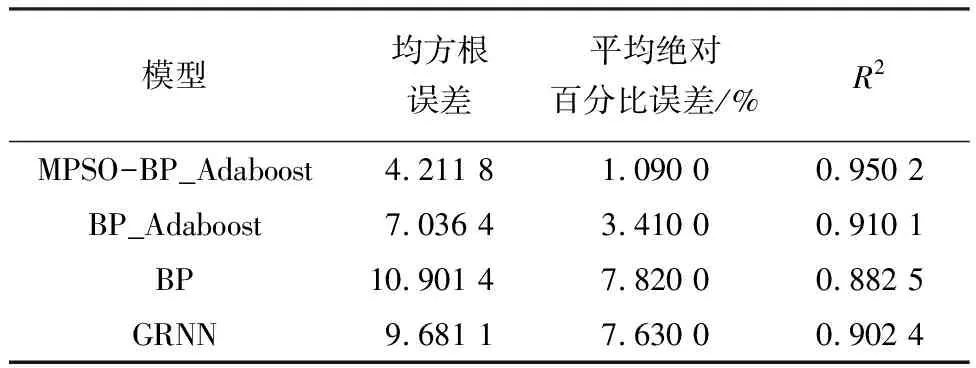
Tab.2 The performance index contrast of four kinds of prediction models at Beijing University of Technology point
模型均方根误差平均绝对百分比误差/%R2MPSO-BP_Adaboost4.211 81.090 00.950 2BP_Adaboost7.036 43.410 00.910 1BP10.901 47.820 00.882 5GRNN9.681 17.630 00.902 4
从表1和2来看,针对两个监测站点数据样本,实验结果略微不同,主要由于万柳监测站数据样本数值变化范围较大,加大了预测难度.为了保证模型有较高预测精度,在数据样本具有真实性和可靠性前提下,数据样本量应该尽可能大,包含不同条件下数据样本信息,使模型训练充分,提高其泛化能力.此外,基于本文实验部分所述建立的MPSO-BP_Adaboost、BP_Adaboost、BP和GRNN 4种预测模型,都具有有效性和可靠性.但是,MPSO-BP_Adaboost预测模型相比于其他3种预测模型而言,均方根误差和平均绝对百分比误差均是最小,R2为最大,这表明改进粒子群优化BP_Adaboost在用于预测大气中PM2.5浓度时,模型性能要优于另外3种预测模型,从而能够更好地实现预测大气中PM2.5浓度的目标,为人们出行提供参考.
4 结 语
本文运用改进粒子群优化BP_Adaboost神经网络来预测北京市海淀区万柳监测站和朝阳区北京工业大学监测点下一个小时PM2.5浓度.根据站点监测数据和神经网络预测输出结果,得出如下结论:(1)影响大气中PM2.5浓度有多种因素,相互之间可能存在强耦合,利用灰色关联分析找出对PM2.5浓度影响较大的因子,并用于BP_Adaboost神经网络建模,可以有效缩短建模时间和更精确建模.(2)BP_Adaboost神经网络是强分类预测器,相比于其他神经网络,在大气预测方面,更利于加强神经网络泛化能力和提高预测模型精度.(3)采用改进粒子群优化BP_Adaboost神经网络,可以有效避免神经网络在训练时陷入局部最优解,进一步改善预测模型性能.在本文中,未能从理论角度去证明改进粒子群算法可以避免陷入局部最优解,这将在以后研究中予以考虑.其次,只做了短期预测,在未来工作中,将尝试去做长期预测,使之更具有实用行和可靠性.最后,由于BP神经网络结构只能凭借试凑法来确定,将考虑用PSO算法去优化网络结构[19-20],解决这一难题并应用于大气中其他污染物浓度预测.
[1] KUMAR U, JAIN V K. ARIMA forecasting of ambient air pollutants (O3, NO, NO2and CO) [J].StochasticEnvironmentalResearchandRiskAssessment, 2010,24(5):751-760.
[2] ELBAYOUMI M, RAMLI N A, YUSOFA N F F M,etal. Multivariate methods for indoor PM10and PM2.5modelling in naturally ventilated schools buildings [J].AtmosphericEnvironment, 2014,94(8):11-21.
[3] ISHAK A B, MOSLAH Z. Analysis and prediction of PM10concentration levels in Tunisia using statistical learning approaches [J].EnvironmentalandEcologicalStatistics, 2016,23(3):1-22.
[4] NIETO P, ANTN J, VILN J,etal. Air quality modeling in the Oviedo urban area (NW Spain) by using multivariate adaptive regression splines [J].EnvironmentalScienceandPollutionResearch, 2015,22(9):6642-6659.
[5] MOUSTRIS K P, ZIOMAS I C, PALIATSOS A G. 3-Day-ahead forecasting of regional pollution index for the pollutants NO2, CO, SO2, and O3using artificial neural networks in Athens, Greece [J].WaterAirandSoilPollution, 2010,209(1/4):29-43.
[6] 孙宝磊,孙 暠,张朝能,等. 基于BP神经网络的大气污染物浓度预测[J]. 环境科学学报, 2016,37(5):1864-1871.
SUN Baolei, SUN Hao, ZHANG Chaoneng,etal. Forecast of air pollutant concentration by BP neural network [J].ActaScientiaeCircumstantiae, 2016,37(5):1864-1871. (in Chinese)
[7] KUKKONEN J, PARTANEN L, KARPPINEN A,etal. Extensive evaluation of neural network models for the prediction of NO2and PM10concentrations, compared with a deterministic modelling system and measurements in central Helsinki [J].AtmosphereEnvironment, 2003,37(4):4539-4550.
[8] 石灵芝,邓启红,路 婵,等. 基于BP人工神经网络大气颗粒物 PM10浓度预测[J]. 中南大学学报(自然科学版), 2012,43(5):1969-1974.
SHI Lingzhi, DENG Qihong, LU Chan,etal. Prediction of PM10mass concentrations based on BP artificial neural network [J].JournalofCentralSouthUniversity(ScienceandTechnology), 2012,43(5):1969-1974. (in Chinese)
[9] ELANGASINGHE M A, SINGHAL N, DIRKS K N,etal. Complex time series analysis of PM10and PM2.5for a coastal site using artificial neural network modelling andk-means clustering [J].AtmosphericEnvironment, 2014,94(1):106-116.
[10] 李 航. 统计学习方法[M]. 北京:清华大学出版社, 2012.
LI Hang.StatisticalLearningMethods[M]. Beijing: Tsinghua University Press, 2012. (in Chinese)
[11] GAO Yun, WEI Xin, ZHUANG Wenqin,etal. QoE prediction for IPTV based on BP_adaboost neural networks [C] //201713thInternationalWirelessCommunicationsandMobileComputingConference(IWCMC). Valencia: IEEE, 2017:32-37.
[12] TSAI M S, HSU F Y. Application of grey correlation analysis in evolutionary programming for distribution system feeder reconfiguration [J].IEEETransactionsonPowerSystems, 2010,25(2):1126-1133.
[13] 罗庆成,徐国新. 灰色关联分析与应用[M]. 南京:江苏科学技术出版社, 1989:110-125.
LUO Qingcheng, XU Guoxin.TheAnalysisApplicationofGreyCorrelation[M]. Nanjing: Jiangsu Science and Technology Publishing House, 1989:110-125. (in Chinese)
[14] HASTIE T, TIBSHIRANI R, FRIEDMAN J.TheElementsofStatisticalLearning[M]. New York: Springer, 2001:337-384.
[15] 王小川,史 峰. MATLAB神经网络43个案例分析[M]. 北京:北京航空航天大学出版社, 2013:115-126.
WANG Xiaochuan, SHI Feng.TheAnalysisof43NeuralNetworkCasesUsingMATLAB[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2013:115-126. (in Chinese)
[16] 钱 锋. 粒子群算法及其工业应用[M]. 北京:科学出版社, 2013:120-156.
QIAN Feng.ParticlesSwarmOptimizationandItsIndustrialApplication[M]. Beijing: Science Press, 2013:120-156. (in Chinese)
[17] ZHENG Yu, CAPRA L, WOLFSON O,etal. Urban computing:concepts, methodologies, and applications [J].ACMTransactionsonIntelligentSystemsandTechnology, 2014,5(3):112-118.
[18] 曹军骥. PM2.5与环境[M]. 北京:科学出版社, 2014.
CAO Junji.PM2.5andtheEnvironmentinChina[M]. Beijing: Science Press, 2014. (in Chinese)
[19] WU Jiansheng, JIN Long. Study on the meteorological factor prediction model using the learning algorithm of neural ensemble based on PSO algorithm [J].JournalofTropicalMeteorology, 2009,15(1):83-88.
[20] SHEIKHAN M, SHA′BANI A A. PSO-optimized modular neural network trained by OWO-HWO algorithm for fault location in analog circuits [J].NeuralComputingandApplications, 2013,23(2):519-530.

