面向智能挖掘机的最优挖掘轨迹规划
孙 伟, 李 二 洋, 王 晓 邦, 郭 正 刚, 李 旭 东, 宋 学 官
( 大连理工大学 机械工程学院, 辽宁 大连 116024 )
0 引 言
大型矿用挖掘机工作效率高、施工稳定性好、环境适应能力强,一直被广泛应用于煤矿、铁矿等露天矿场的作业中[1].但是长期以来大型矿用挖掘机的操作完全依赖工人经验,不仅挖掘效率低下,而且故障频发.因此针对其智能化与自动化方面的研究已逐渐成为各国相关研究机构的研究热点[2-3].智能挖掘机的自动作业规划能提高挖掘机工作的安全性和控制的准确性,减小驱动系统和执行系统的冲击振动,使挖掘机运行更加平稳,挖掘能耗以及操作人员的工作强度降低[4].近年来,国内外诸多学者针对挖掘机的控制参数做了很多研究.申立军[5]以挖掘后角、提升绳与斗杆中心夹角为目标函数,对挖掘机提升和推压速度进行了优化设计,使挖掘过程更加平稳.Wei等[6]提出了一种新的挖掘阻力计算模型,通过对轨迹进行多项式曲线拟合,并优化多项式方程系数,得到了近似最优轨迹.Awuah-Offei等[7]在对挖掘机进行动力学分析的基础上,以挖掘单位质量的物料所消耗的能量为目标函数,对挖掘机提升和推压速度进行了优化.上述研究大多只针对特定形状的料堆,以挖掘后角变化最小为目标函数进行优化,而没有计算最佳后角的方法;不仅如此,研究中还忽略了电机的加速和减速过程,对挖掘机整个挖掘过程的预测存在一定的局限性,并不适用于智能挖掘机[8-9].
本文针对上述研究中存在的问题,基于McKyes等[10-11]挖掘阻力预测模型,综合考虑物料的重力、铲斗与物料间的摩擦力以及速度和铲斗两侧物料对挖掘阻力的影响,构建一种适用于大型矿用挖掘机的动态挖掘阻力预测模型,并在新的挖掘阻力预测模型的基础上,提出一种能量最优的挖掘机自动作业规划方案,实现挖掘机作业时针对不同料堆形状的轨迹规划,为智能挖掘机的连续作业提供理论基础.
1 数学模型的建立
1.1 智能挖掘流程
智能挖掘机的构成如图1所示,其工作流程为:挖掘机在得到作业任务后,通过3D扫描仪得到物料的料堆形状,然后通过控制系统计算得出挖掘最优轨迹并转化成控制参数,执行机构在提升机构和推压机构的共同驱动下完成挖掘过程.
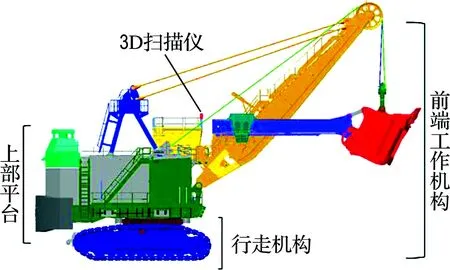
图1 智能挖掘机的构成Fig.1 The composition of intelligent excavator
1.2 挖掘轨迹的计算
如图2所示,挖掘机作业时铲斗在提升机构和推压机构的配合下插入料堆底部(A点);然后铲斗向前向上运动,此过程中,被挖掘物料逐渐流入铲斗内,运动到B点时,推压机构停止运动,推压杆长度不再变化;提升机构继续运动,开始抽斗,直至铲斗离开料堆(C点),完成挖掘.挖掘过程完成后,回转机构驱动挖掘机上部平台旋转至卸料位置(装载卡车处),打开斗门卸料,然后再复位到挖掘起始位置,一次挖掘过程完成.行走机构驱动挖掘机向前运动,进入下一次挖掘过程.
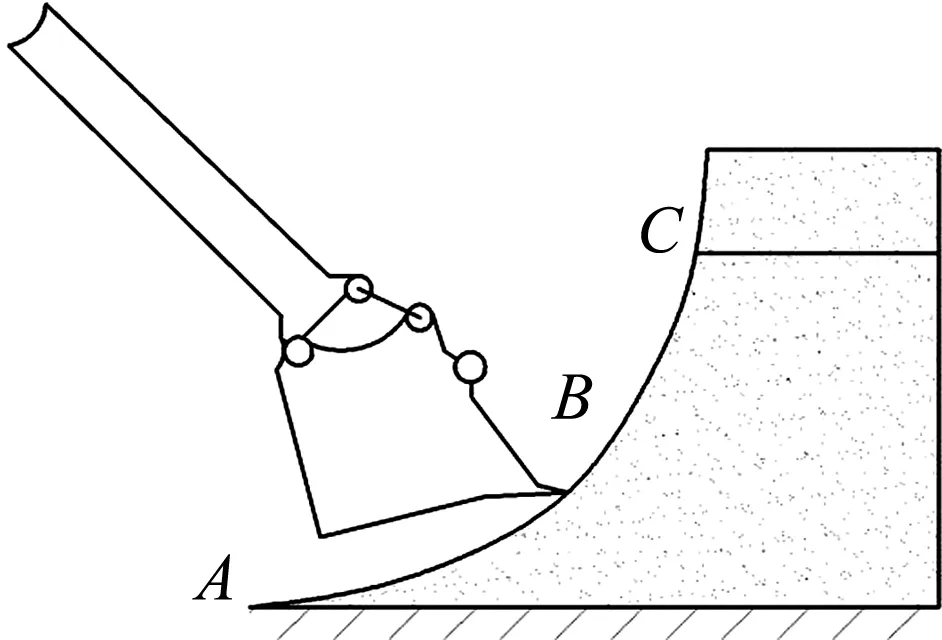
图2 挖掘机挖掘轨迹Fig.2 The excavating trajectory of excavator
因为本文研究对象为单斗杆挖掘机,铲斗姿态只和推压运动、提升运动以及挖掘机的初始姿态有关,在任意位置,铲斗只有一种姿态.因此,挖掘机的挖掘轨迹即为斗齿齿尖划过的轨迹,如图3所示.

图3 挖掘机的工作过程Fig.3 Excavator working process
如图4所示,挖掘过程中推压机构和提升机构的运动为加速—匀速—减速,其速度可以用分段函数表示为
(1)
(2)
式中:vg、vs分别为推压机构、提升机构的输出速度;tug、tdg分别为推压机构加速、减速时间;ag为推压机构加速度;tg为推压机构运行时间;tus、tds分别为提升机构加速、减速时间;as为提升机构加速度;ts为提升机构运行时间.
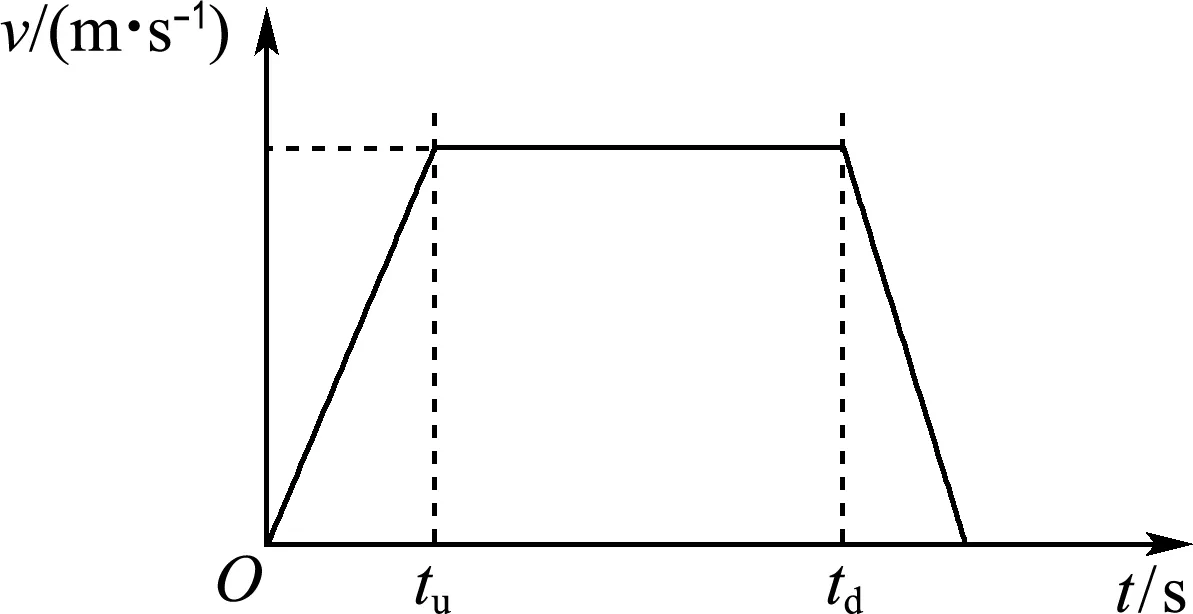
图4 挖掘机构速度曲线Fig.4 Speed curve of excavating device
挖掘机工作过程中的主要参数如图5所示,在推压机构的输出速度vg和提升机构的输出速度vs已知的基础上,通过几何关系可知:以物料的底端为原点,以水平方向为X轴,竖直方向为Y轴,建立直角坐标系,挖掘过程中齿尖D点的切向速度vt和法向速度vn分别为
(3)
式中:A7为提升绳与斗杆的夹角.
水平、竖直速度为
vx=vtcosA3+vnsinA3
(4)
vy=vtsinA3-vncosA3
(5)
式中:A3为极径与竖直方向的夹角.
则斗齿齿尖的轨迹方程为
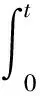
(6)
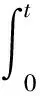
(7)
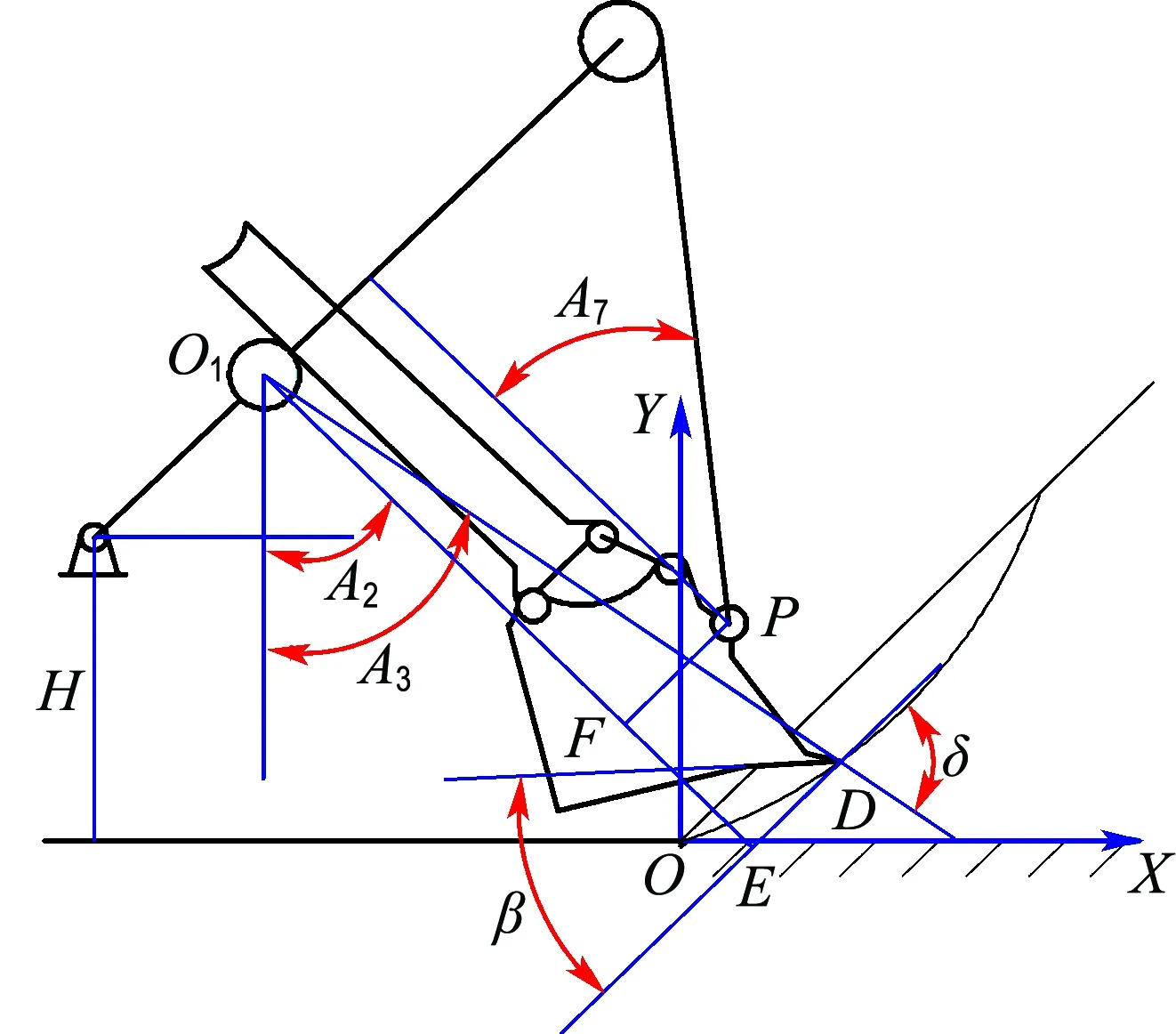
图5 挖掘过程中参数关系Fig.5 Parameter relation in the process of excavating
1.3 挖掘深度d和挖掘体积V的计算
首先,定义挖掘深度为斗齿齿尖到物料表面的最小距离.由图6可知,任意一点的挖掘深度为
d=(Xtanλ-Y)cosλ
(8)
式中:λ为物料斜面与水平方向的夹角.
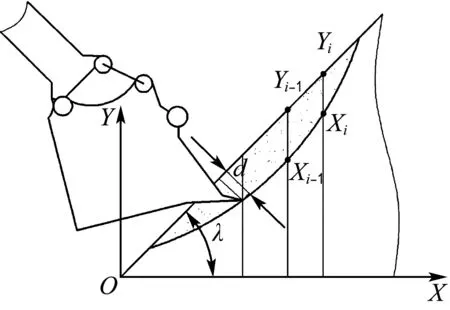
图6 挖掘体积示意图Fig.6 Excavating volume schematic
在理想情况下,挖掘体积等于铲斗齿尖D点扫过的面积S与铲斗宽度B的乘积,即
V=BS
(9)
在计算挖掘体积时可以把挖掘轨迹离散化,挖掘体积可以通过累加每个小段的体积得到.可知每一段小区间内铲斗铲装物料的体积为
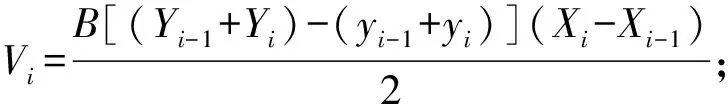
i=1,2,3,…,n
(10)
式中:Yi-1、Yi为齿尖轨迹的纵坐标.
则整个挖掘过程中挖掘体积为
(11)
1.4 挖掘阻力的计算
挖掘机的主要任务是进行矿石装载,在工作过程中,被挖掘物料对铲斗产生很大的阻力,这是挖掘机构主要的工作荷载[12-13].因此,一个符合实际测试的挖掘阻力模型,对于挖掘机构的设计和性能分析非常重要.现有的挖掘阻力模型有经验模型和理论模型两种.传统的挖掘阻力计算公式大多采用苏联的经验公式[14-15]:
P=KBd
(12)
式中:K为挖掘比阻力,是被挖掘对象的特征;d为挖掘深度.
考虑到整个挖掘过程是动态的,其挖掘角度、挖掘深度、挖掘速度等参数都是时刻变化的,所以此公式并不适用于整个挖掘过程中挖掘阻力的计算.因此本文在McKyes机-土静力平衡方程[12]阻力计算模型的基础上,综合考虑物料的重力、铲斗与物料间的摩擦力以及速度和铲斗两侧物料对挖掘阻力的影响,构建了一种新的动态挖掘阻力预测模型,如图7所示.
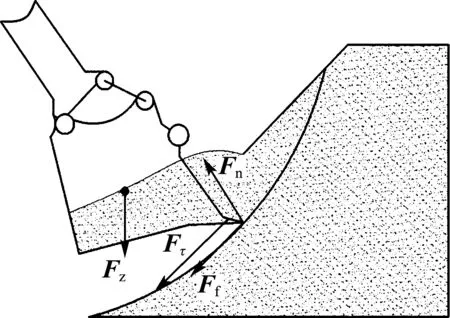
图7 挖掘过程受力分析Fig.7 Force analysis of excavating process F=Fz+Fτ+Fn+Ff
(13)
式中:Fz为物料和铲斗本身的重力,方向始终竖直向下,并随着挖掘过程的进行逐渐增大,直到挖掘结束,其数值为
Fz=γVg+mdg
(14)
其中md为铲斗质量.
Fτ为切削阻力,主要包括McKyes切向阻力T,速度影响带来的附加阻力Fv,以及铲斗两侧物料影响带来的阻力Fc.
T=w(γgd2Nγ+cdNc+γv2dNa)
(15)
其中Nγ=0.5(cotβ+cotρ)/e,Nc=[1+cotρcot(ρ+φ)]/e,Na=[tanρ+cot(ρ+φ)e]/(1+tanρcotβ),e=cos(β+δ)+sin(β+δ)cot(ρ+φ).
(16)

(17)
式中:β为挖掘后角;δ为机-土摩擦角;φ为内摩擦角;g为重力加速度;γ为物料密度;c为土壤内聚力;ρ为土壤滑裂面倾角.
Fn为由于挤压物料产生的法向阻力,其垂直于铲斗运动方向,与挖掘机操作及物料的硬度和状态相关,很难用解析式表达.
Ff是由Fn产生的摩擦力,其数值为
Ff=Fntanδ
(18)
对于爆破后的矿石,在挖掘机操作适当的情况下,法向阻力与切向阻力的比值ψ=0.30~0.45,即
Fn=ψFτ
(19)
因此Fn的数值大小可以通过法向阻力与切向阻力的比值得出:
(20)
图8为机械式挖掘机在挖掘过程中任意位置处的受力状况,主要的受力包括铲斗斗尖位置处的挖掘阻力Fz、Fn;钢丝绳提升力Fs,在此不考虑天轮的传递效率;铲斗和物料的重力Fz、斗杆的重力G2;推压齿轮齿条的推压力Fg.
以推压轴中心O1为原点取矩∑MO1=0,即
-Fgr+FsO1PsinA5-G2sin(A2+A4)O1C-
FzO1Qsin(A2+A3)-Fgr+FτrhosinA3+
FnDE/rho=0
(21)
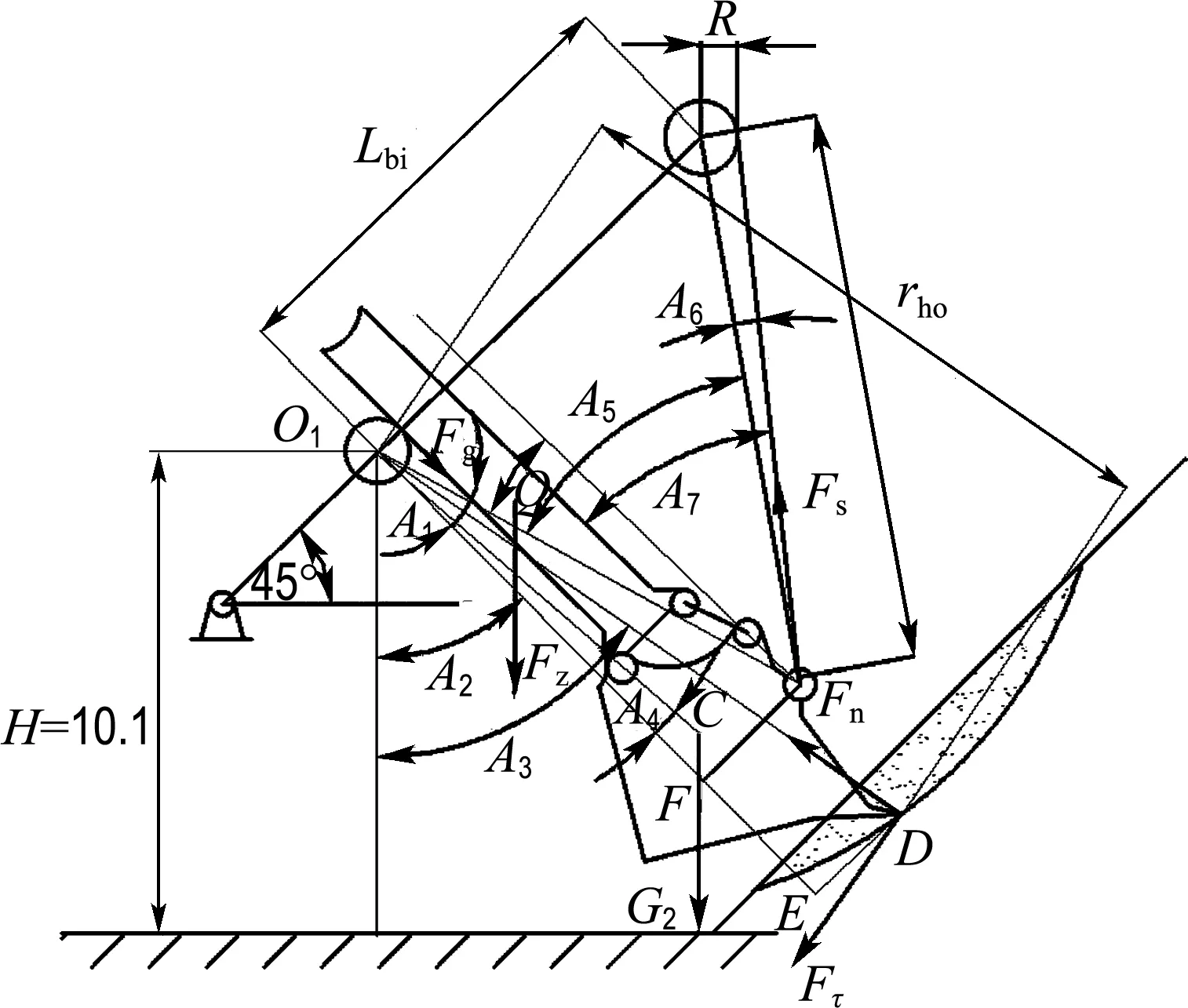
图8 挖掘阻力分解示意图Fig.8 Excavating resistance decomposition diagram
将力分别沿着斗杆方向进行分解,建立平衡方程:
Fncos(A3-A2)-G2cosA4-FzcosA1+
Fτtan(A3-A2)+FscosA7-Fg=0
(22)
其中未知量为钢丝绳的提升力Fs、推压齿轮齿条的推压力Fg,两个方程可求得两个未知量.
1.5 模型验证
验证阻力模型的方法主要有模型之间相互验证和实测结果验证两种方法.但是,由于现有的挖掘阻力模型都有不同的假设条件,这些模型之间很难相互验证.因此,验证模型的最好方式是进行实验,将模型的结果与实测的数据进行比较.为了验证阻力模型的准确性,选用了太原重工股份有限公司WK-55挖掘机进行阻力测试,测试的工况参数如表1所示.

表1 阻力计算中用到的参数
WK-55挖掘机采用安装在控制柜内的变频器控制推压与提升电机进行挖掘作业,因此可以直接通过变频器采集挖掘过程中的电流、电压的历时变化,并以挖掘机电机的电压和电流为输入值计算得到电机的实际输出扭矩,并根据式(23)、(24)转化为提升绳和推压杆的输出力.
挖掘机推压力
Fg=Tcicηc/Rp
(23)
式中:Tc为推压电机的输出扭矩;ic=39.6,为推压机构总传动比;ηc=0.807,为推压机构总传动效率;Rp=0.368,为推压小齿轮节圆半径.
挖掘机提升力
Fs=2Thihηh/Rd
(24)
式中:Th为单个提升电机的输出扭矩;ih=51.061,为提升机构总传动比;ηh=0.884,为提升机构总传动效率;Rd=0.864,为提升钢丝绳在提升卷筒上的缠绕半径.
以WK-55挖掘机挖掘堆角为38°物料时的实测阻力与相同控制参数下的模型计算结果进行对比,如图9所示.结果显示:挖掘阻力模型计算结果与实测结果很接近,并且略微偏小,这是由于未计入装载阻力及斗侧壁摩擦力所致,也说明了这两部分在阻力中所占的比重不大.

(a) 提升绳受力
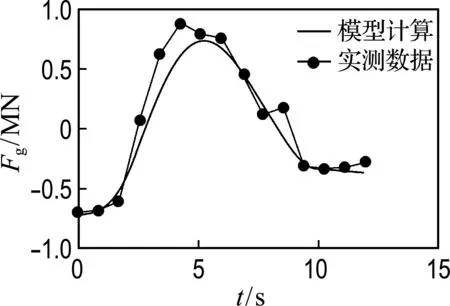
(b) 推压杆受力
图9 提升绳和推压杆受力随时间变化历程
Fig.9 The hoist and crowd force changes with time
2 优化设计模型的建立
2.1 挖掘机能耗计算模型
在挖掘作业过程中,挖掘速度从零开始增加,到挖掘结束阶段又降为零,即整个系统的总动能不变.因此,挖掘有效功耗可分为重力能耗和阻力能耗,其本质为两个电机(提升电机和推压电机)做功,挖掘过程中两个驱动做功分别为
(25)
2.2 目标函数
大型矿用挖掘机主要用于采矿以及装载作业,在挖掘过程中主要以斗杆的推压运动和提升绳的提升运动为主.如何在满足满斗率的条件下,使挖掘能耗最小,历来是人们关心的问题.因此本文将挖掘机作业时挖掘单位质量的物料所消耗的能量作为目标函数:
(26)
式中:m为流入铲斗内的物料的质量.
2.3 设计变量
影响挖掘机能耗的参数很多,归纳起来有以下3种:物料参数、结构参数、控制参数.为实现挖掘机的智能化,需要对挖掘机的整个挖掘过程包括推压和提升电机的加速、减速过程进行优化设计,以便智能挖掘机针对不同的料堆形状选择不同的控制参数.本文以推压电机的加速时间tug、减速时间tdg、加速度ag,提升电机的加速时间tus、减速时间tds、加速度as以及初始位置时斗杆与竖直方向的夹角θ0(图10)作为设计变量,如下式所示:
x=(tugtdgagθ0tustdsas)
(27)

图10 斗杆与竖直方向夹角Fig.10 The included angle between bucket pod and the vertical direction
2.4 约束条件
挖掘机作业时工作装置的主要约束条件包括挖掘体积约束、结构参数约束和性能约束.其中结构参数约束指的是挖掘机作业过程中所受到的自身结构尺寸的限制而能够达到的极限位置;性能约束指的是挖掘机作业时必须保证较高的挖掘效率且不能使电机超负荷运转.
(1)挖掘体积约束
为了保证挖掘机的工作效率,挖掘过程必须保证90%以上的满斗率且不能过大,可表示为
Vmin≤V≤Vmax
(28)
式中:Vmin为最小挖掘体积;Vmax为最大挖掘体积.
(2)结构参数约束
挖掘机作业过程中要受到自身结构尺寸的约束,主要包括:
斗杆长度约束
p≤pmax
(29)
式中:pmax为斗杆的最大长度.
挖掘高度约束
hmin≤h≤hmax
(30)
式中:hmin为铲斗出料时的最小高度;hmax为铲斗能达到的最大高度.
(3)电机性能约束
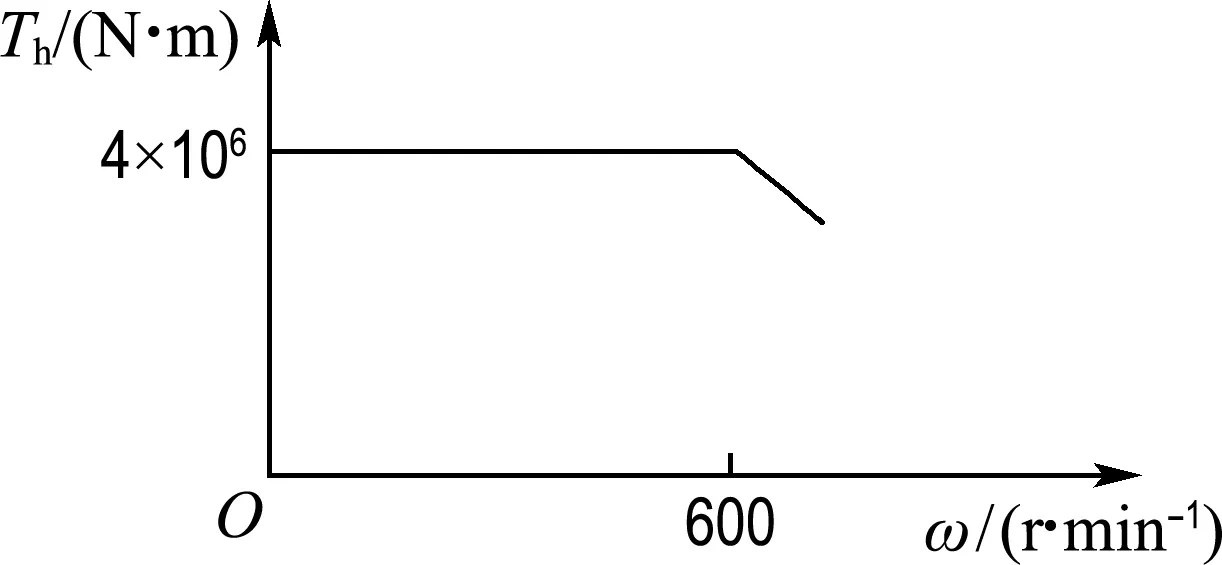
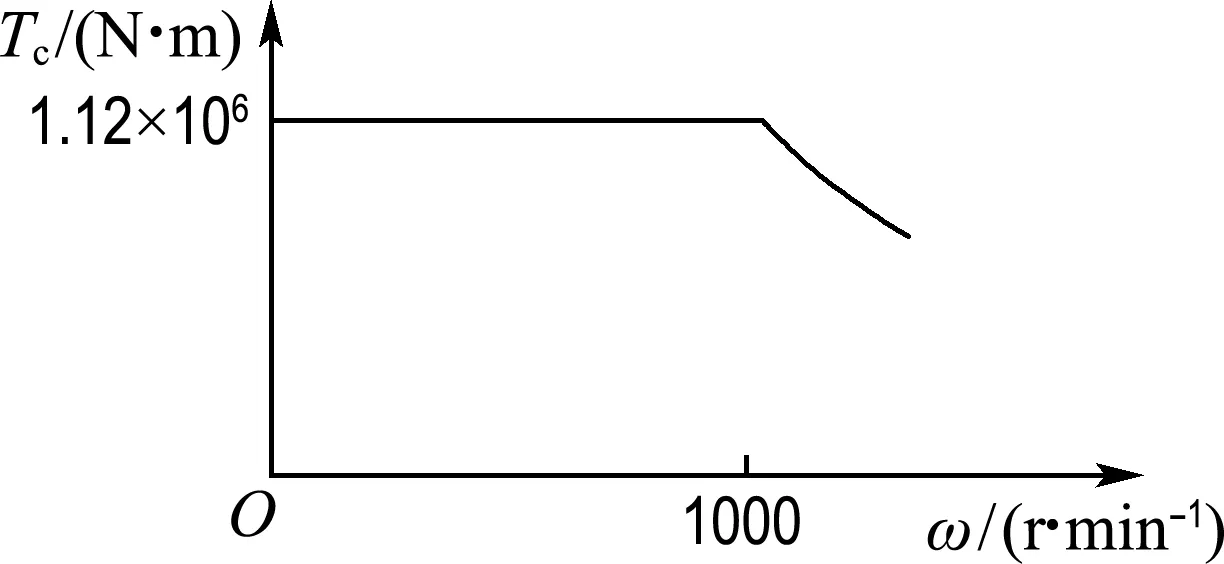
WK-55挖掘机提升和推压电机的功率特性曲线如图11所示.
挖掘机作业时,受电机性能影响,挖掘机的提升、推压电机功率必须在其功率特性曲线之内,即

P≤
(31)
式中:P为电机输出功率,

P-
为电机最大输出功率.
综上所述,可以得到优化问题的标准形式为
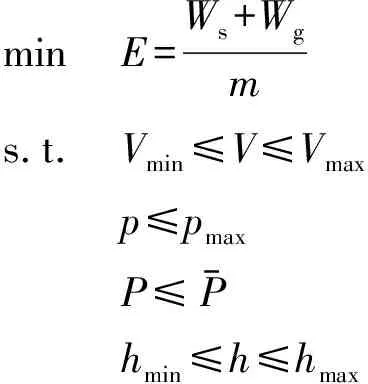
minE=Ws+Wgms.t.Vmin≤V≤Vmaxp≤pmaxP≤P-hmin≤h≤hmax
(32)
(a) 提升电机
(b) 推压电机
图11 提升和推压电机功率特性曲线
Fig.11 The hoist and crowd motor power characteristic curves
3 模型应用
根据上述大型矿用挖掘机优化设计数学模型,以WK-55挖掘机为例进行最优控制的优化设计.WK-55挖掘机主要被应用在露天矿场的剥离作业中,其主要参数如表2所示.本文主要应用对象为矿山采矿时爆破后的石块,属于散体物料.
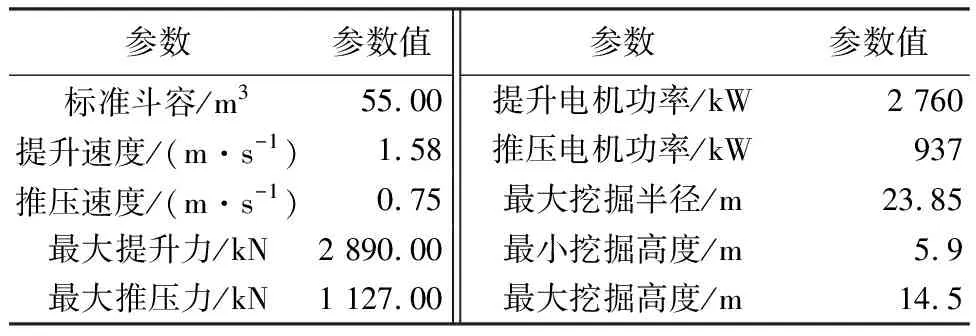
表2 WK-55挖掘机主要工作参数
综合考虑挖掘机性能参数以及智能挖掘机的设计要求,确定挖掘机优化模型的参数,并将其代入式(32)中,最终得到其优化模型如式(33)所示.在Matlab中编写优化程序,应用遗传算法分别对堆角为38°、43°、48°的料堆进行挖掘轨迹优化.优化后设计变量取值及挖掘作业性能对比分别如表3、4以及图12所示.
(33)
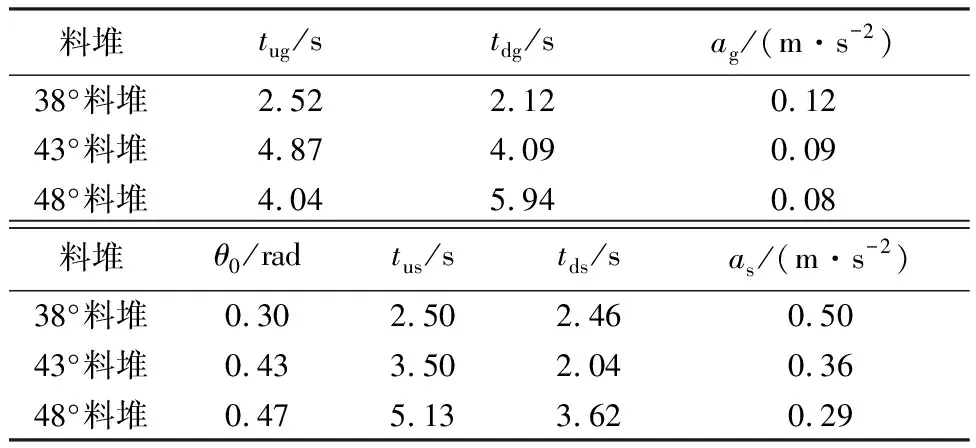
表3 优化前后参数对比
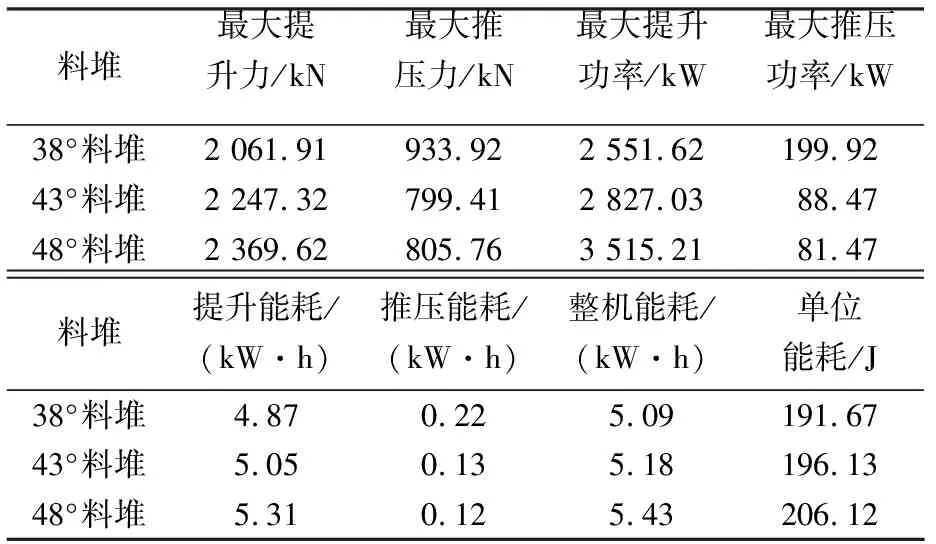
表4 最优控制下作业性能
综合分析表3和4中数据可以发现,对于任意料堆,都有一条最优挖掘轨迹,可以保证挖掘能耗最低.根据测试结果,正在服役的WK-55挖掘机挖掘料堆角分别为38°、43°、48°的料堆的平均单位能耗为232.71 J/kg,而在使用挖掘轨迹规划时的挖掘能耗为197.97 J/kg,降低了14.9%,挖掘能耗有效降低.
同时,轨迹规划下的电机速度保持平稳变化,与正在服役的挖掘机电机运行速度相比,其电机速度明显减小,大大降低了对电机的设计要求,如图12所示.
此外,轨迹规划方法可以有效减小挖掘阻力,与此同时,相比于手动控制,轨迹规划下的挖掘轨迹既能保证满斗率又能避免挖掘过程中的冲击振动,使电机的力矩变化更加平稳,降低了故障率.
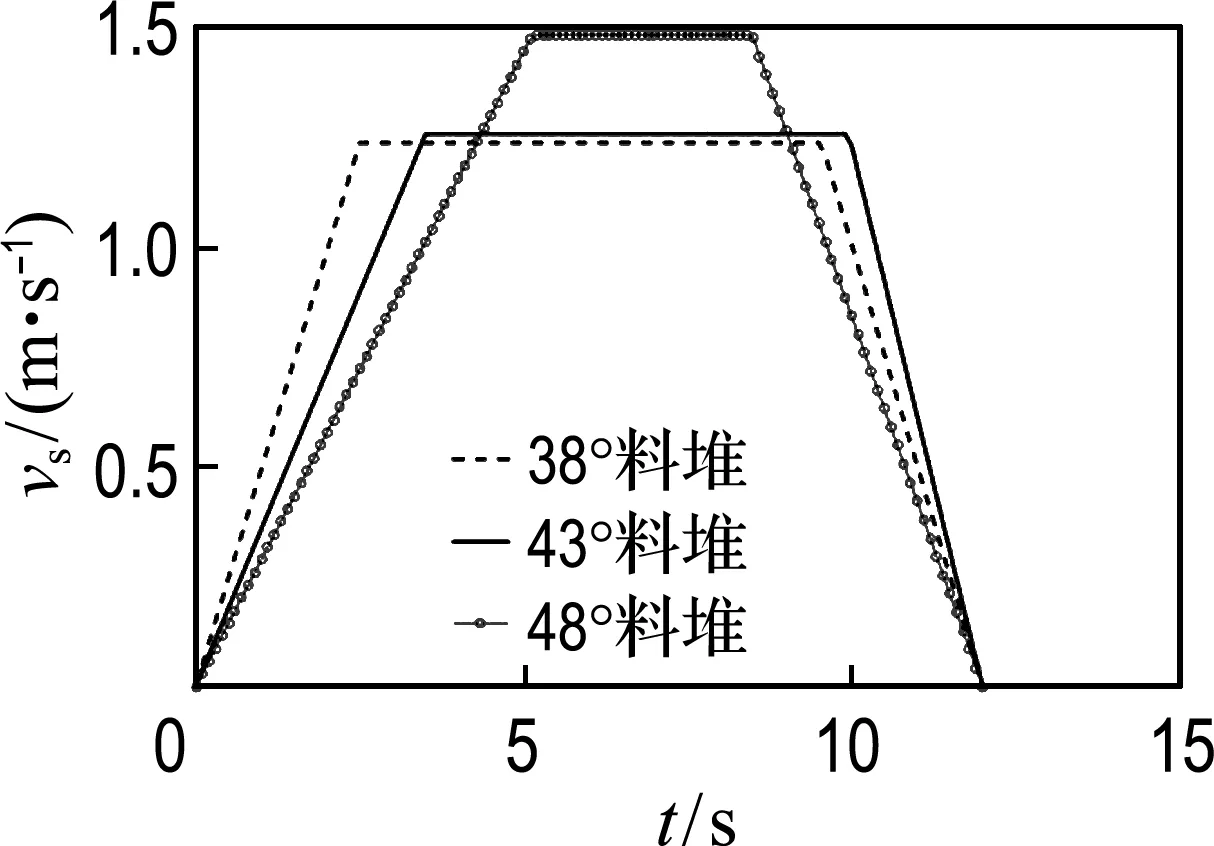
(a) 提升速度
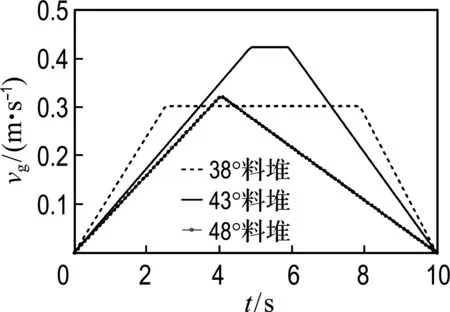
(b) 推压速度
(c) 38°料堆挖掘轨迹
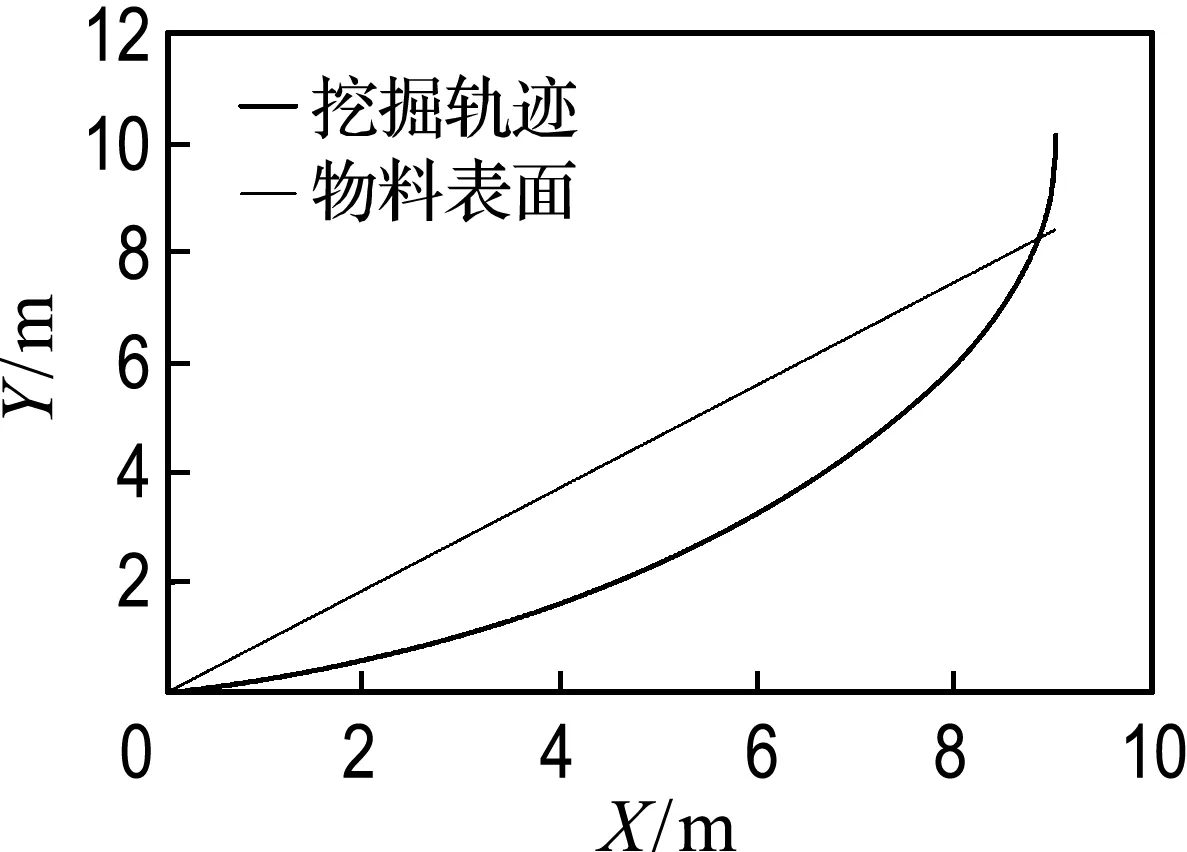
(d) 43°料堆挖掘轨迹
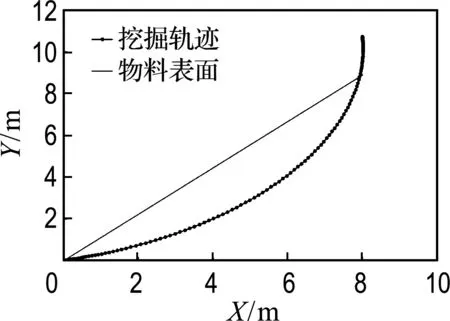
(e) 48°料堆挖掘轨迹
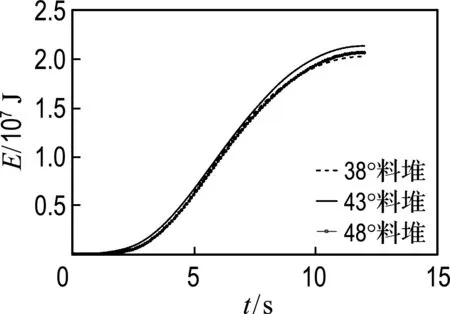
(f) 3种料堆形状的挖掘能耗
图12 轨迹规划下的速度、轨迹、能耗曲线
Fig.12 The curves of speed,trajectory,energy consumption of trajectory programming
4 结 论
(1)在McKyes机-土静力平衡方程阻力计算模型的基础上,综合考虑物料的重力、铲斗与物料间的摩擦力、速度和铲斗两侧物料对挖掘阻力的影响,构建了一种新的动态挖掘阻力预测模型,并在此基础上给出了挖掘机挖掘工作过程中的能耗计算方法.
(2)以实现挖掘机的智能化、工作装置轨迹控制的自动化为目的,在综合考虑结构和性能的基础上,以料堆角为38°、43°、48°的料堆为例进行了控制参数优化,在保证挖掘效率的前提下,降低了挖掘能耗,实现了在智能挖掘机连续作业过程中,根据不同的料堆形状实时调整挖掘轨迹的功能,为智能挖掘机的研发提供了理论指导.
(3)在设定约束条件时,根据现役挖掘机的单次挖掘时间,将优化过程中的挖掘机完成单次完整挖掘的时间设置为定值.在后续的研究中,可以针对挖掘时间和挖掘能量同时进行优化,并用多种曲线形式拟合电机速度曲线[16],以得到时间和能量最优的挖掘机最优控制参数.
[1] 贺继林,赵 鑫,张大庆,等. 新型智能挖掘机自动轨迹控制研究[J]. 广西大学学报(自然科学版), 2012(2):259-265.
HE Jilin, ZHAO Xin, ZHANG Daqing,etal. Trajectory control of new intelligent excavator [J].JournalofGuangxiUniversity(NaturalScienceEdition), 2012(2):259-265. (in Chinese)
[2] 邵 辉,胡伟石,罗继亮,等. 自动挖掘机的动作规划[J]. 控制工程, 2012,19(4):594-597.
SHAO Hui, HU Weishi, LUO Jiliang,etal. Action planning of automatic excavator [J].ControlEngineeringofChina, 2012,19(4):594-597. (in Chinese)
[3] 刘心昊,张大庆,赵喻明,等. 一种新型智能挖掘机的设计与实现[J]. 建筑机械, 2010(9):100-102.
LIU Xinhao, ZHANG Daqing, ZHAO Yuming,etal. Design and realization of a novel intelligent excavator [J].ConstructionMachinery, 2010(9):100-102. (in Chinese)
[4] 谭 琛,宋伟奇. 液压挖掘机智能化设计研究[J]. 液压与气动, 2016(9):38-43.
TAN Chen, SONG Weiqi. Intelligent design and research of hydraulic excavator [J].ChineseHydraulics&Pneumatics, 2016(9):38-43. (in Chinese)
[5] 申立军. 机械式挖掘机工作装置机构性能研究与优化设计平台研发[D]. 长春:吉林大学, 2013.
SHEN Lijun. Study on performance and development of optimization design software of mechanical mining shovel mechanism [D]. Changchun: Jilin University, 2013. (in Chinese)
[6] WEI Baochen, GAO Feng. Digging trajectory optimization for a new excavating mechanism of electric mining shovel [C] //ProceedingsoftheASMEDesignEngineeringTechnicalConference. New York: American Society of Mechanical Engineers, 2012: 1033-1039.
[7] AWUAH-OFFEI K, FRIMPONG S. Cable shovel digging optimization for energy efficiency [J].MechanismandMachineTheory, 2007,42(7):995-1006.
[8] 徐弓岳,丁华锋,孙玉玉. 基于改进非支配排序遗传算法的正铲挖掘机工作装置优化设计[J]. 机械工程学报, 2016,52(21):35-43.
XU Gongyue, DING Huafeng, SUN Yuyu. Optimization of face-shovel excavator′s attachment based on improved NSGA-II [J].JournalofMechanicalEngineering, 2016,52(21):35-43. (in Chinese)
[9] MCKYES E, ALI O S. Cutting of soil by narrow blades [J].JournalofTerramechanics, 1977,14(2):43-58.
[10] MCKYES E. Calculation of draft forces and soil failure boundaries of narrow cutting blades [J].TransactionsoftheAmericanSocietyofAgriculturalEngineers, 1978,21(1):20-24.
[11] SWICK W C, PERUMPRAL J V. A model for predicting soil-tool interaction [J].JournalofTerramechanics, 1988,25(1):43-56.
[12] MCKYES E. Soil cutting and tillage [M] //DevelopmentsinAgriculturalEngineering7. Amsterdam: Elsevier, 1985.
[13] FRIMPONG S, LI Ying. Stress loading of the cable shovel boom under in-situ digging conditions [J].EngineeringFailureAnalysis, 2007,14(4):702-715.
[14] 张卫国,权 龙,程 珩,等. 基于真实载荷的挖掘机工作装置瞬态动力学分析[J]. 机械工程学报, 2011,47(12):144-149.
ZHANG Weiguo, QUAN Long, CHENG Hang,etal. Transient dynamic analysis on working device of excavator based on practical load [J].JournalofMechanicalEngineering, 2011,47(12):144-149. (in Chinese)
[15] 阎书文. 机械式挖掘机设计[M]. 北京:机械工业出版社, 1982:1-24.
YAN Shuwen.MechanicalExcavatorDesign[M]. Beijing: China Machine Press, 1982:1-24. (in Chinese)
[16] SONG Xueguan, LV Liye, LI Jieling,etal. An advanced and robust ensemble surrogate model:extended adaptive hybrid functions [J].JournalofMechanicalDesign,TransactionsoftheASME, 2018,140(4):041402.

