基于特征分块的视差图像拼接算法

张晶晶,翟东海,2,黄莉芝,喻 强

(1.西南交通大学 信息科学与技术学院,成都 611756; 2.西藏大学 工学院,拉萨 850000)

0 概述

图像拼接一直是计算机视觉和图形图像领域研究的热点和难点[1-2],图像拼接就是把同一场景下不同时间、不同视角或不同传感器获取的一组相互间有重叠部分的图像序列进行图像配准,经重采样和融合后形成一幅包含各图像序列信息的宽视角场景的、完整的、高清晰的新图像的技术[3]。图像拼接技术被广泛地应用于环境监测、天气预报、摄影测量学、遥感图像处理[4]、虚拟环境重建、计算机视觉等领域[5]。

目前,图像拼接领域最为流行的算法是基于尺度不变特征(SIFT)算法[6],该算法具有尺度不变性和旋转不变性。但是,这种基于单应性矩阵的方法只有在输入图像视差很小的情况下才可以很好地工作,当输入图像有很大的视差时就会产生重影。文献[7]提出DHW(Dual Homography Warps)双平面变形算法,该算法将图像分为back plan 和ground plan 2个平面,采用2个单应性矩阵对2个平面进行投影变换,但当场景中出现大结构物体时该算法的拼接结果很不理想。文献[8]提出了CPW(Content Preserving Warps)算法,该算法采用位置变换约束和形状扭曲约束对目标图像进行逼近相似变换,这样可以将配准误差降至最低并保留场景的刚度,但是当原图像与目标图像之间存在较大的平移和旋转时由于刚性约束的限制,该算法的拼接效果会大大降低,出现模糊和重影。文献[9]提出一种改进的SIFT配准算法,采用一种自适应的混合线性算法对重合区域图像变换至HIS颜色空间进行图像拼接,该算法可以提高配准的精度,但它仍然不适合处理大视差图像拼接。文献[10]提出基于AP聚类图像分块的角点检测改进算法,当聚类中心点和尺度参数没选好时会影响角点检测的精度。文献[11]提出一种APAP(As-Projective-As-Possible)变换模型,该模型用全局单应性矩阵代替基本单应性矩阵,强调全局投影特性,同时允许局部非投影偏差,在一定程度上缓解了视差造成的拼接误差。但是当处理两幅大视差图像时单应性矩阵不能处理视差,还需要借用其他技术来消除视差造成的重影和结构扭曲。文献[12]提出基于3点匹配的图像拼接算法,用6参数仿射矩阵来简化图像的转换关系,计算速度快,但是不能处理视差图像的拼接。

本文针对上述问题,提出一种基于特征分块的视差图像拼接算法,通过特征分块快速确定图像之间的特征匹配块,求出全局单应性矩阵,进行局部优化消除拼接过程中的重影和形状扭曲,以实现大视差图像拼接。

1 视差图像拼接算法框架

图像拼接主要包含以下4步:相机标定,图像预处理,图像配准,图像融合,其中最关键的步骤是图像配准。

具体步骤如下:

1)采用张正友相机标定法[13]求出相机的内参、外参和畸变系数,对相机进行矫正。

2)图像预处理,进行图像去噪、图像增强和颜色空间变换,然后采用图割算法[14]将参考图像I1和目标图像I2分割成若干个具有独特性质的图像块,并将图像块编号。

3)图像配准,用SIFT算法对图像进行特征提取,在特征描述子中加入特征点的图像块信息,确定目标图像与参考图像之间的特征匹配图像块,根据特征匹配块确定图像之间的重叠区域和非重叠区域。

本文的视差图像拼接流程如图1所示。

图1 基于特征点的图像拼接流程

2 基于特征分块的视差图像拼接

2.1 特征分块的必要性

进行特征分块的原因主要有以下3点:

1)现有的算法在进行图像拼接时都是随机地从特征匹配点集合中挑选特征匹配点来计算单应性矩阵;然后判断是否绝大多数特征点都满足所求的单应性变换模型,如果满足则用所求的单应性矩阵对图像进行配准,如果不满足则需要重新挑选匹配特征点来计算单应性变换模型,迭代进行上述步骤直到绝大多数点都满足单应性变换模型。但是,这种随机挑选特征匹配点的算法会出现挑选的特征点过于集中的情况,在这种情况下计算得到的单应性矩阵不具有全局性,只有少数点满足单应性变换模型,会增加算法的迭代次数。通过对参考图像I1和目标图像I2进行特征分块可以实现:计算全局单应性矩阵时,如果每次分别从各个块中都选取匹配点可以使求出的单应性矩阵更具有全局性的特性,使尽可能多的点满足变换模型H,提高H的配准质量减少迭代次数。

2)文献[15]指出SIFT算法中全图像域特征点的检测与描述和特征点的匹配是2个最消耗时间的步骤。然而,在实际图像匹配过程中,正确的特征点匹配对仅集中分布在图像间的重叠区域内,非重叠区域内特征点不存在正确的匹配点对,即为无效区域。文献[16]提出只有分布在重叠区域的特征点才是用于匹配的有用特征点。所以,图像匹配具有区域性,通过特征分块可以快速地确定图像间的重叠区域和非重叠区域,避免非重叠区域的干扰,提高匹配的效率和准确率。

2.2 参考图像和目标图像之间的特征匹配图像块

确定特征匹配图像块过程如下:

1)用图割算法将参考图像和目标图像分割成图像块,对每一个图像块进行编号,如图2所示。

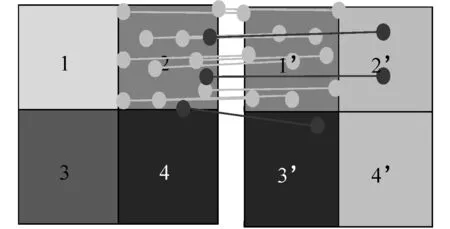
图2 特征匹配图像块

2)运用SIFT算法对图像进行特征提取,在进行特征描述时加入特征点所属的图像块信息,没加图像块信息时每个特征点的特征描述子是一个128维的向量S(s1,s2,…,s128);加入图像块信息后每个特征点有129维信息S(s1,s2,…,s129),s129表示特征点所属的图像块。但是在对描述子进行匹配时只计算前128维信息之间的匹配程度,图像块信息s129将在后面确定图像块匹配时用到。

3)分别找出参考图像的各个图像块的特征匹配块,如图3所示,I1的图像块2和I2的图像块1′是匹配块,I1的图像块4和I2的图像块3′是匹配块。确定图像匹配块的方法详见步骤4)。

图3 全局单应性矩阵Hi的匹配质量

4)以参考图像I1中的图像块2为例,求图像块2的匹配图像块步骤如下:

(1)找出参考图像的图像块2的特征点集合,记为P2j(j=1,2,…,N2,表示特征点集合中总共有N2个特征点,j表示第j个特征点)。

按上述方法求出参考图像I1中各个图像块对应的特征匹配块,其中非重叠区域没有匹配的特征点对,所以没有对应的特征匹配块,如参考图像I1中的图像块1和图像块3没有特征匹配块。

2.3 全局单应性矩阵

特征分块法计算单应性矩阵的步骤如下:

1)找出参考图像和目标图像之间对应的特征匹配块区域I1i和I2i′(I1i表示参考图像I1的第i个图像块,I2i′表示目标图像I2的第i′个图像块)。

2)根据特征匹配块,将图像的特征匹配点的集合P分成M个子集P=∑Pi(i=1,2,…,M)。

3)分别从不同的特征匹配块对应的特征匹配点子集Pi中挑选特征匹配点求单应性矩阵Hi,这样可以避免随机抽选特征点过于集中的情况,保证计算出的单应性矩阵的全局性。

本文算法根据特征匹配块,确定参考图像I1与目标图像I2之间的重叠图像块,删除非重叠区域,只计算重叠图像块的配准质量。而且可以分别计算每个特征匹配块的配准质量,如图3所示,分别计算<1,1′>、<2,2′>、<3,3′>、<4,4′>特征匹配块的配准质量,这样不仅可以提高计算速度还可以提高计算精度。因为1只和1′是匹配的图像块,本文算法避免了计算图像块1和2′,1和3′,1和4′之间的匹配质量,这样可以减少计算量和误差。

3 重影消除与扭曲的局部优化

用最优全局单应性矩阵对参考图像和目标图像进行预配准之后,还需要对重叠区域进行局部优化消除视差造成的重影和形状扭曲。本文给重叠区域的每对图像块加入形状扭曲约束和图像网格块链接约束,可以较好地消除重影和形状扭曲。

3.1 形状扭曲约束

(1)

(2)

图4 三角形2个顶点组成的局部坐标系

3.2 网格块链接约束

图5 参照图像和局部优化图像之间的图像块链接约束

(3)

同理,根据图5(e)、图5(f)获得了网格块之间的垂直链接约束公式:

(4)

同理,根据图5(g)和图5(h)获得了网格块之间的对角链接约束公式:

(5)

所以,网格块之间的链接约束可以表示为:

El=El1+El2+El3

(6)

将形状扭曲约束和网格块链接约束的能量公式合并,得到如式(7)所示的总的能量公式,通过求能量公式的最小值实现局部优化。

E=αEs+βEl

(7)

其中,α、β是权重值,α=0.4、β=0.6上述最小值问题是二次方程问题,通过求解一个稀疏的线性方程可以得到最小化的结果。

对局部优化后的结果进行图像融合得到最终的消除重影的扭曲的拼接图像。

4 实验结果与分析

本文实验在Matlab环境下运行,实验在已有的图像库中随机抽出了大量的标准图像来进行实验,将本文算法与CPW[8]算法和APAP[11]算法进行对比。实验都为大小为1 000×740像素的自然图像。实验结果如图6～图8所示。观察实验结果可以发现,CPW算法[8]只使用了位置变化约束和形状扭曲约束对图像进行变换,由于刚性变换的限制导致拼接结果中出现重影(图中用圆圈圈出)。APAP算法[11]在局部优化时,使用移动直接线性变换(moving DLT)对图像进行尽可能配准,该算法尝试将2幅图像的重叠区域尽可能地对齐导致拼接结果出现形状扭曲(图中用圆圈圈出),本文算法可以较好地消除重影和形状扭曲。

图6 3种算法得到的拼接结果比较1

图7 3种算法得到的拼接结果比较2

图8 3种算法得到的拼接结果比较3

为定量比较各个算法的拼接效果,通过计算参考图像I1、单应性变换后图像I2的重叠区域之间的均方根误差RMSE和拼接耗时来衡量算法的拼接性能。对于一幅M×N大小的图像而言,参考图像I1的重叠区域与单应性变换后图像I2的重叠区域之间的均方根误差RMSE的公式如式(8)所示。

(8)

其中,I1(x,y)为参考图像,I2(x,y)为单应性变换后图像,RMSE代表了两者的差异,RMSE值越小,表明图像拼接的结果越好。

表1给出了对3组视差图像拼接的均方根误差RMSE和拼接耗时数值结果。对比表1可以发现,CPW算法的拼接效果比较差,虽然耗时最短但是均方根误差RMSE最大。APAP算法与CPW算法相比RMSE明显减小,但拼接耗时明显增加。本文算法与CPW算法相比虽然拼接耗时有所增加,但RMSE值减小较多,本文算法与APAP算法相比RMSE值和拼接耗时都减少很多。综上所述,本文算法在拼接效果上占优势,本文算法在大幅改进拼接效果的同时,运算时间比APAP少,比CPW的运算时间只高了一点,所以通过综合比较,本文算法较有优势。

表1 不同拼接算法的RMSE和耗时比较

5 结束语

[1] PANG S,SUN M,HU X,et al.SGM-based seamline determination for urban orthophoto mosaicking[J].ISPRS Journal of Photogrammetry and Remote Sensing,2016,112:1-12.

[2] 江 铁,朱桂斌,孙 奥.全景图像拼接技术研究现状综述[J].重庆工商大学学报(自然科学版),2012,29(12):60-71.

[3] 盖进伟.一种基于特征点的图像拼接技术研究[D].太原:中北大学,2012.

[4] LI X,HUI N,SHEN H,et al.A robust mosaicking procedure for high spatial resolution remote sensing images[J].ISPRS Journal of Photogrammetry and Remote Sensing,2015,109:108-125.

[5] 刘志文,刘定生,刘 鹏.应用尺度不变特征变换的多源遥感图像特征点匹配[J].光学精密工程,2013,21(8):2146-2153.

[6] LOWE D G.Distinctive image features from scale-invariant key points[J].International Journal of Computer Vision,2004,60(2):91-110.

[7] GAO J,KIM S J,BROWN M S.Constructing image panoramas using dual-homography warping[C]//Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Press,2011:49-56.

[8] LIU F,GLEICHER M,JIN H,et al.Content-preserving warps for 3D video stabilization[J].ACM Transactions on Graphics,2009,28(3):44.

[9] 张永梅,张晨希,郭 莎.基于SIFT特征的彩色图像拼接方法研究[J].计算机测量与控制,2016,24(8):236-239.

[10] 刘文进,张 蕾,孙劲光.基于AP聚类图像分块的角点检测改进方法[J].计算机工程,2015,41(4):217-221.

[11] ZARAGOZA J,CHIN T J,BROWN M S,et al.As-projective-as-possible image stitching with moving DLT[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Press,2013:2339-2346.

[12] 刘德连,张建奇.基于3点匹配的图像拼接算法[J].计算机工程,2006,32(13):203-205.

[13] ZHANG Z.A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.

[14] van de SSNDE K E A,UIJLINGS J R R,GEVERS T,et al.Segmentation as selective search for object recognition[C]//Proceedings of 2011 IEEE International Conference on Computer Vision.Washington D.C.,USA:IEEE Press,2011:1879-1886.

[15] 李玉峰,李广泽,谷绍湖,等.基于区域分块与尺度不变特征变换的图像拼接算法[J].光学精密工程,2016,24(5):1197-1205.

[16] 杜京义,胡益民,刘宇程.基于区域分块的SIFT图像匹配技术研究与实现[J].光电工程,2013,40(8):52-58.

[17] 韩 冰,王永明.基于一种快速归一化积相关算法的图像匹配研究[J].兵工学报,2010,31(2):160-165.