基于非均匀光滑有限元法的含圆孔功能梯度压电板应力和电场集中因子分析

蔡斌，周立明



基于非均匀光滑有限元法的含圆孔功能梯度压电板应力和电场集中因子分析

蔡斌1，周立明2

(1. 吉林建筑大学 土木工程学院，吉林 长春，130118；2. 吉林大学 机械科学与工程学院，吉林 长春，130025)

为提高含圆孔功能梯度压电板应力和电场集中因子的求解精度，提出含圆孔功能梯度压电板的力电耦合非均匀基于单元的光滑有限元法。采用高斯点处的真实材料属性进行计算，分析材料属性按某一方向呈指数函数梯度变化时含孔功能梯度压电板应力和电场集中因子，并与非均匀有限元求解结果进行对比。研究结果表明：该方法求解力电耦合作用下功能梯度压电板的应力集中因子和电场集中因子具有较高的精度。

功能梯度压电材料；非均匀光滑有限元法；应力集中因子；电场集中因子

功能梯度压电材料是新一代高性能多功能材料，其结构的完整性直接影响着他们的应用领域。由于功能梯度压电材料兼备压电材料和功能梯度材料的优点，具有良好的机电耦合特性，被广泛应用于智能先进结构中。在工程应用中，功能梯度压电元件往往以板、壳的结构形式存在，在力电载荷作用下，常常会因为制备过程中的缺陷(如孔洞、裂纹、夹杂物和分层等)发生疲劳断裂或介质击穿导致结构功能失效，因此，求解含孔功能梯度压电材料板的应力和电场集中因子对提升相关器件性能具有重要意义。目前，人们已在功能梯度压电材料这一领域[1−3]开展较多研究。NOURMOHAMMADI等[4−5]对功能梯度压电板的多场耦合问题进行了分析。SELIM等[6]基于高阶剪切变形理论对功能梯度压电板的振动问题进行了研究。ZHAO等[7]基于无网格法对不同载荷作用下功梯度压电板的静态弯曲问题进行了分析。KOMIJANI等[8]分析了多物理场下功能梯度压电材料执行器非线性响应问题。DAI等[9]对功能梯度压电材料的反平面裂纹问题进行了研究。JODAEI[10]基于微分求积法对不同边界条件下功梯度压电板的静态问题进行了分析。RANGELOV等[11−12]采用边界积分方程法对功能梯度压电材料的平面和反平面断裂问题进行了研究。孟广伟等[13]采用扩展无网格法对含孔功能梯度压电板的应力集中问题进行了研究。然而，对含孔功能梯度压电体应力和电场集中因子的求解还有待于进一步研究。由于功能梯度压电材料的非均匀性和多场耦合特性，使得求解离散方程的难度大大增加。在基于单元的数值方法中，往往因为系统刚度偏硬，导致力场和电场计算出现误差。为了降低离散系统刚度，LIU 等[14−16]提出基于梯度光滑技术的有限元算法。NGUYEN-VAN等[17]将光滑有限元法拓展到压电材料中，之后，NGUYEN-XUAN等[18−19]基于边光滑有限元法对二维压电结构静力力学问题进行了研究，发现光滑有限元可提高解的精度，具有广阔的应用前景。本文作者推导出含孔功能梯度压电板的力电耦合非均匀基于单元的光滑有限元法，求解含孔功能梯度压电板应力和电场集中因子，讨论材料属性按某一方向呈指数函数梯度变化时功能梯度压电板的力学响应，并与有限元(FEM)求解结果进行对比。

1 基本方程

功能梯度压电材料场基本方程为

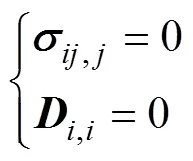
应变和电场相容方程为

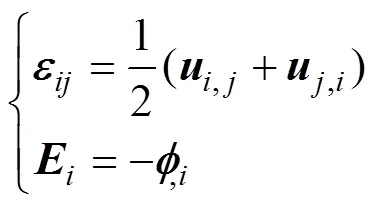
本构方程为

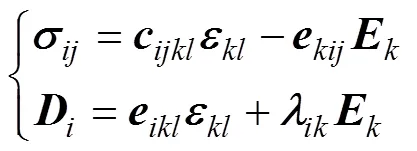
功能梯度压电材料物参服从指数分布规律：

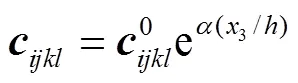
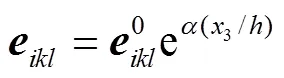
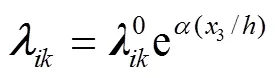
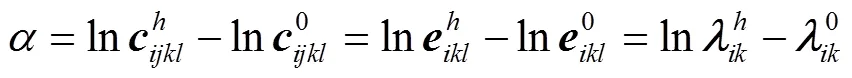
对于横观各向同性功能梯度压电板，在坐标1−3平面内满足：

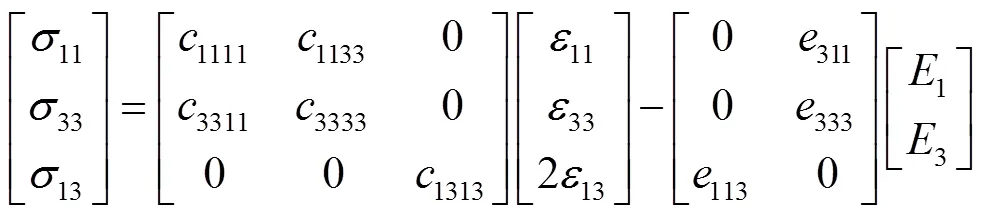
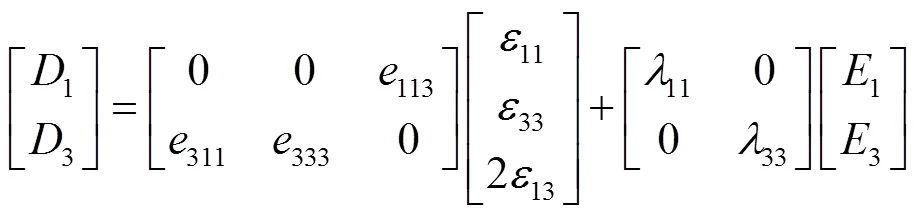
2 非均匀基于单元的光滑有限元法

将求解域离散成p个单元，包含n个节点，每个单元内的广义位移向量和广义电势向量表示为：

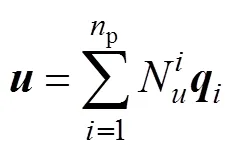
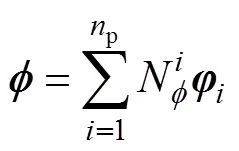
式中：N和分别为非均匀基于单元的光滑有限元(ICS-FEM)位移形函数和电势形函数；和分别为节点位移向量和节点电势向量。

将四节点单元划分为4个光滑子元，场节点、边中间光滑节点、中心光滑节点、边高斯点、外法向向量分布情况及形函数如图1所示。

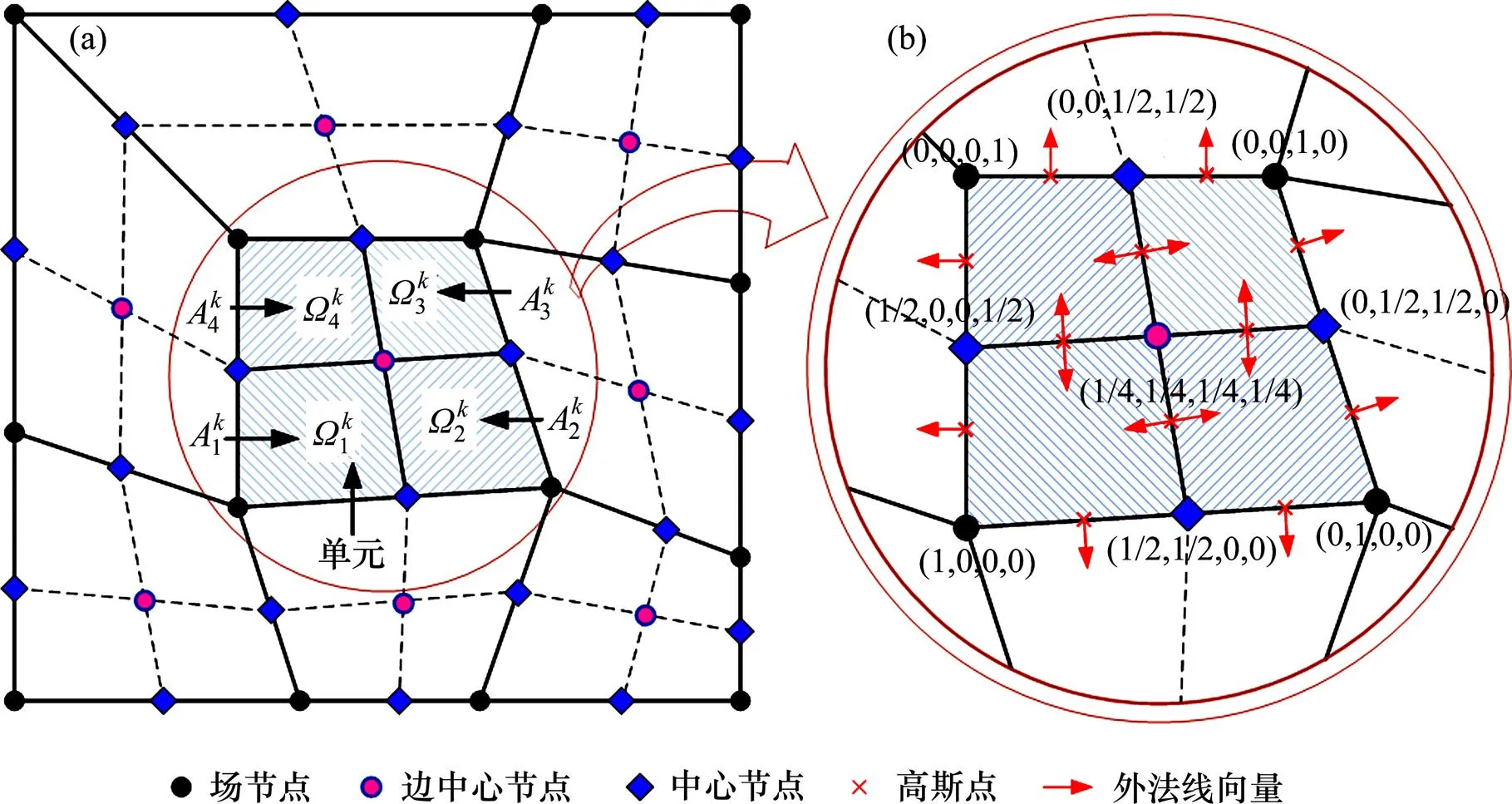
(a) 光滑子元；(b) 形函数值

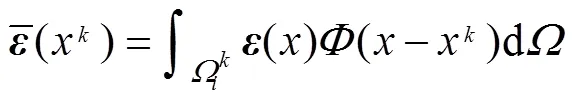
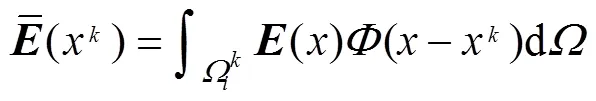
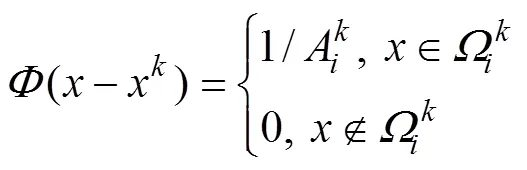
式中：

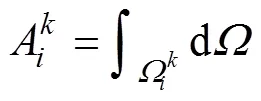
将式(14)代入式(12)和(13)可得

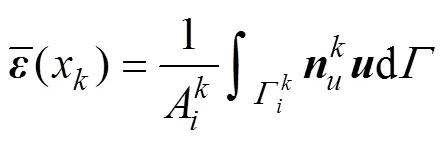
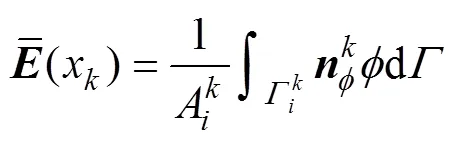
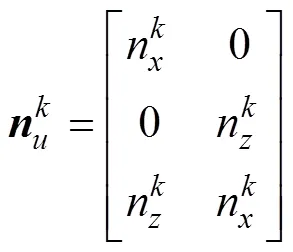
将式(16)和式(17)改写为：

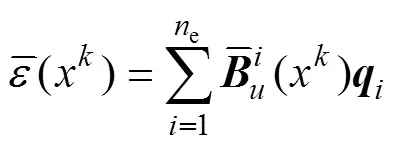
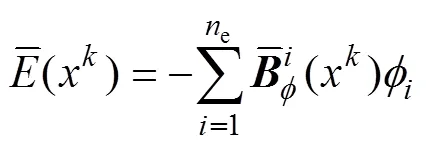
式中：e为光滑子元个数。

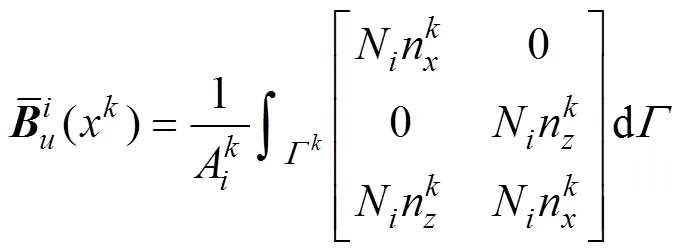
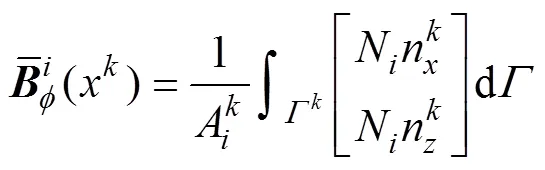
式中：N为相关节点的形函数。

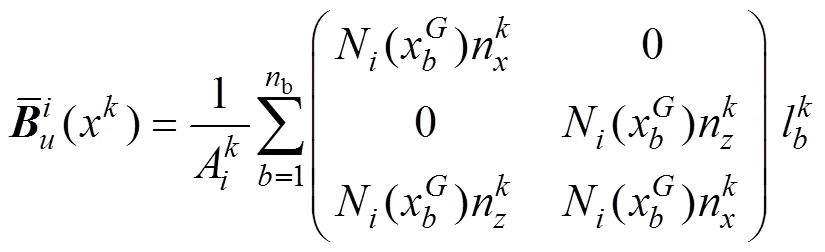
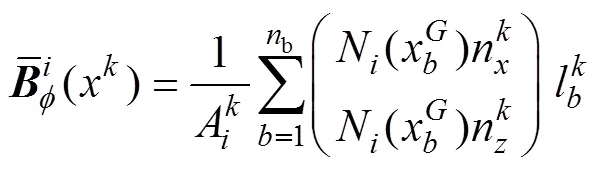
功能梯度压电耦合系统的平衡方程如下：

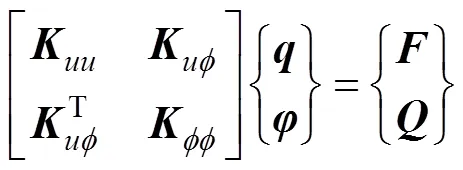
式中各刚度矩阵表达式如下：

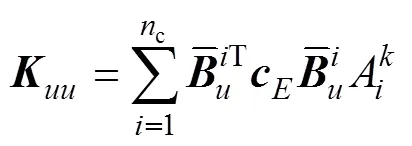
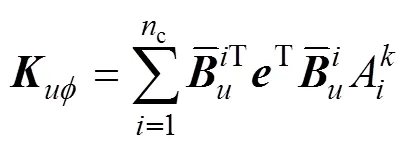
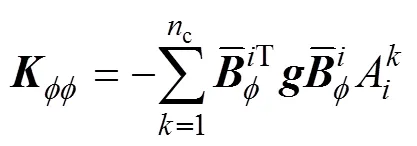
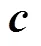
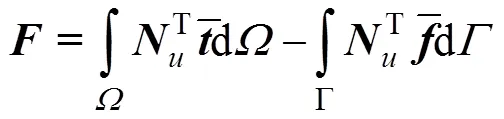
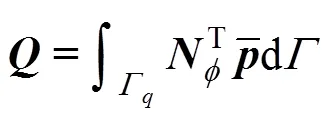
3 数值算例

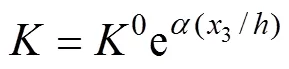
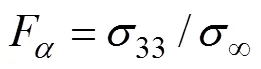
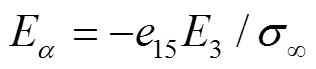
图3所示为离散单元。表2和表3所示分别为底部材料为P−7和PZT−H5时，采用非均匀基于单元的光滑有限元法(SFEM)和非均匀有限元法(FEM)计算含圆孔功能梯度压电材料板应力集中因子和电场集中因子的结果对比。取非均匀有限元法离散20 000个单元的求解结果为参考解。由表2~3可知：在相同网格数下，SFEM精度高于FEM精度，SFEM是正确有效的。

图4所示为采用SFEM和FEM求解得到不同梯度参数(为0，0.2，0.5和1.0)下功能梯度压电板(P−7为底边)的应力云图和电场强度云图。由图4可知：SFEM的相关数值高于FEM的数值，说明将梯度光滑技术引入非均匀有限元可降低其系统刚度，提高求解精度。

图3 离散单元

表1 材料常数

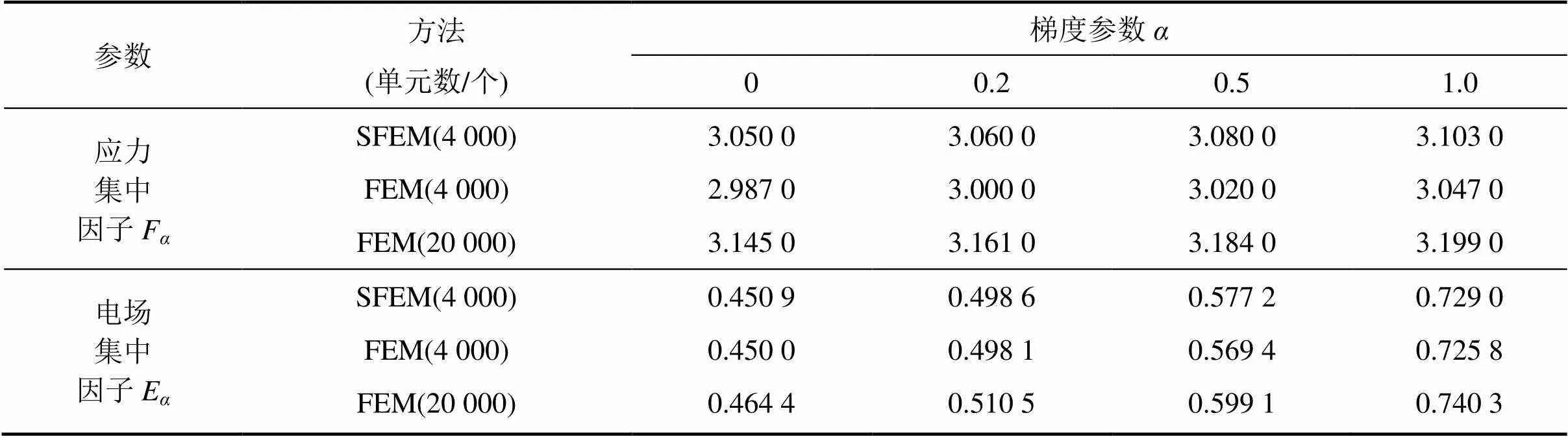
表2 底部材料为P−7时应力集中因子和电场集中因子的结果对比

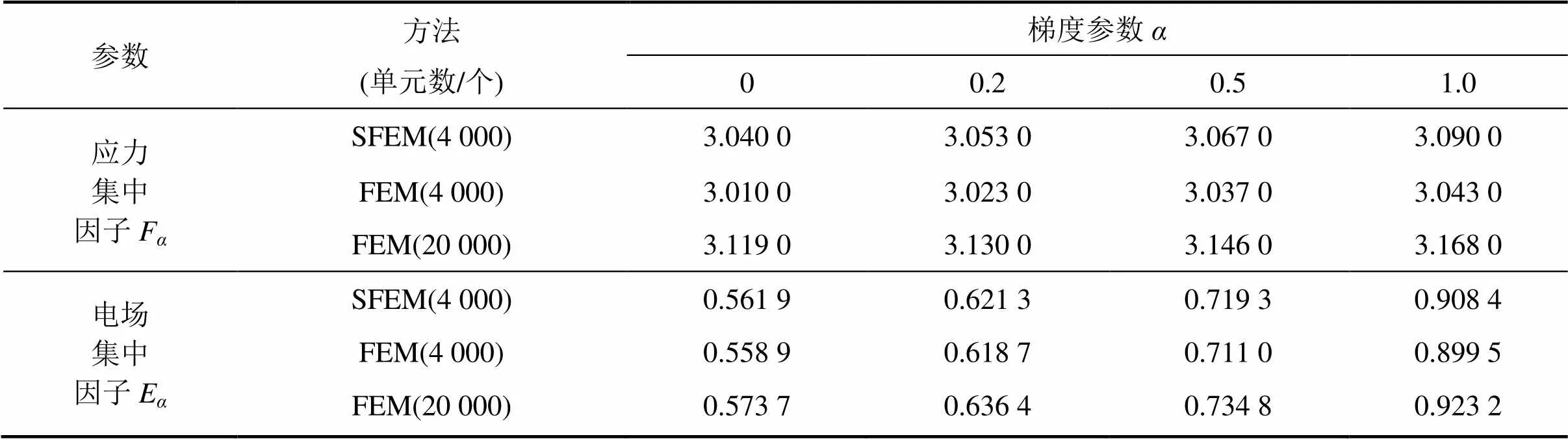
表3 底部材料为PZT−H5时应力集中因子和电场集中因子的结果对比

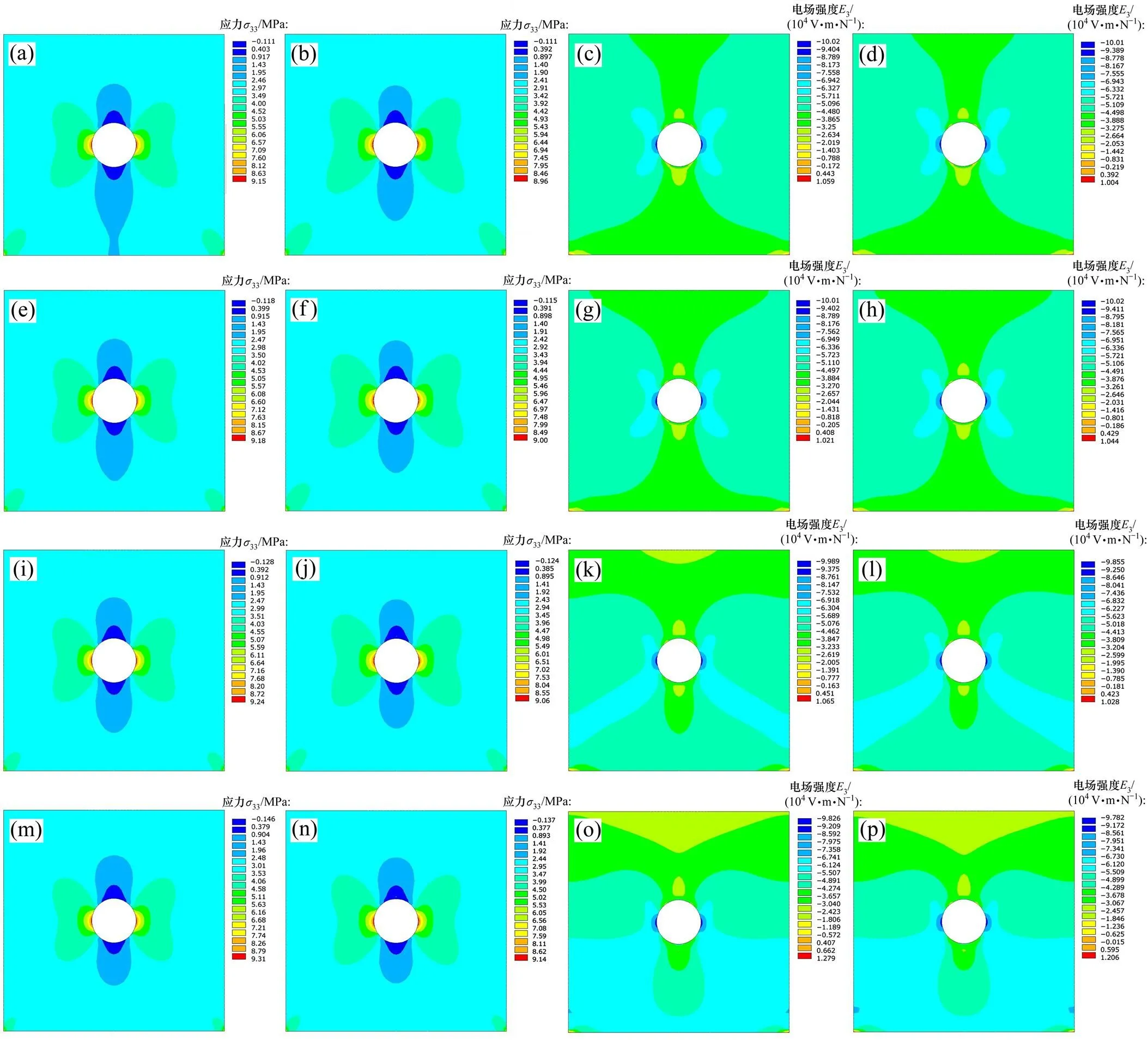
(a) 应力云图(SFEM，=0)；(b) 应力云图(FEM，=0)­­；(c) 电场强度云图(SFEM，=0)；(d) 电场强度云图(FEM，=0)；(e) 应力云图(SFEM，=0.2)；(f) 应力云图(FEM，=0.2)；(g) 电场强度云图(SFEM，=0.2)；(h) 电场强度云图(FEM，=0.2)；(i) 应力云图(SFEM，=0.5)；(j) 应力云图(FEM，=0.5)；(k) 电场强度云图(SFEM，=0.5)；(l) 电场强度云图(FEM，=0.5)；(m) 应力云图(SFEM，=1.0)；(n) 应力云图(FEM，=1.0)；(o) 电场强度云图(SFEM，=1.0)；(p) 电场强度云图(FEM，=1.0)

图4 不同梯度参数下功能梯度压电板(P−7为底边)的应力云图和电场强度云图

Fig. 4 Stress contours and electric field contours of functionally graded piezoelectric plate (P−7 as the base) with varied gradient parameters

图5所示为采用SFEM和FEM求解得到不同梯度参数(为0，0.2，0.5和1.0)下功能梯度压电板(PZT−H5为底边)的应力云图和电场强度云图。由图5可知：SFEM的求解精度高于FEM的求解精度，进一步验证了梯度光滑技术引入非均匀有限元中可降低其系统刚度，提高解的精度；同时也验证了非均匀基于单元的光滑有限元法的正确性与有效性。

从图4和图5可以看出：当梯度参数从0变化到1.0时，应力云图变化不大，应力集中的位置就在圆孔中间位置两侧，应力对材料参数小梯度变化不敏感。当梯度参数从0变化到1.0时，电场集中的位置也在圆孔中间位置两侧，但电场高强度区域有明显增大趋势，这是由于随着梯度参数变大，功能梯度压电板底部材料属性与顶部材料属性差异变大，电场强度对材料参数小梯度变化较敏感所导致。

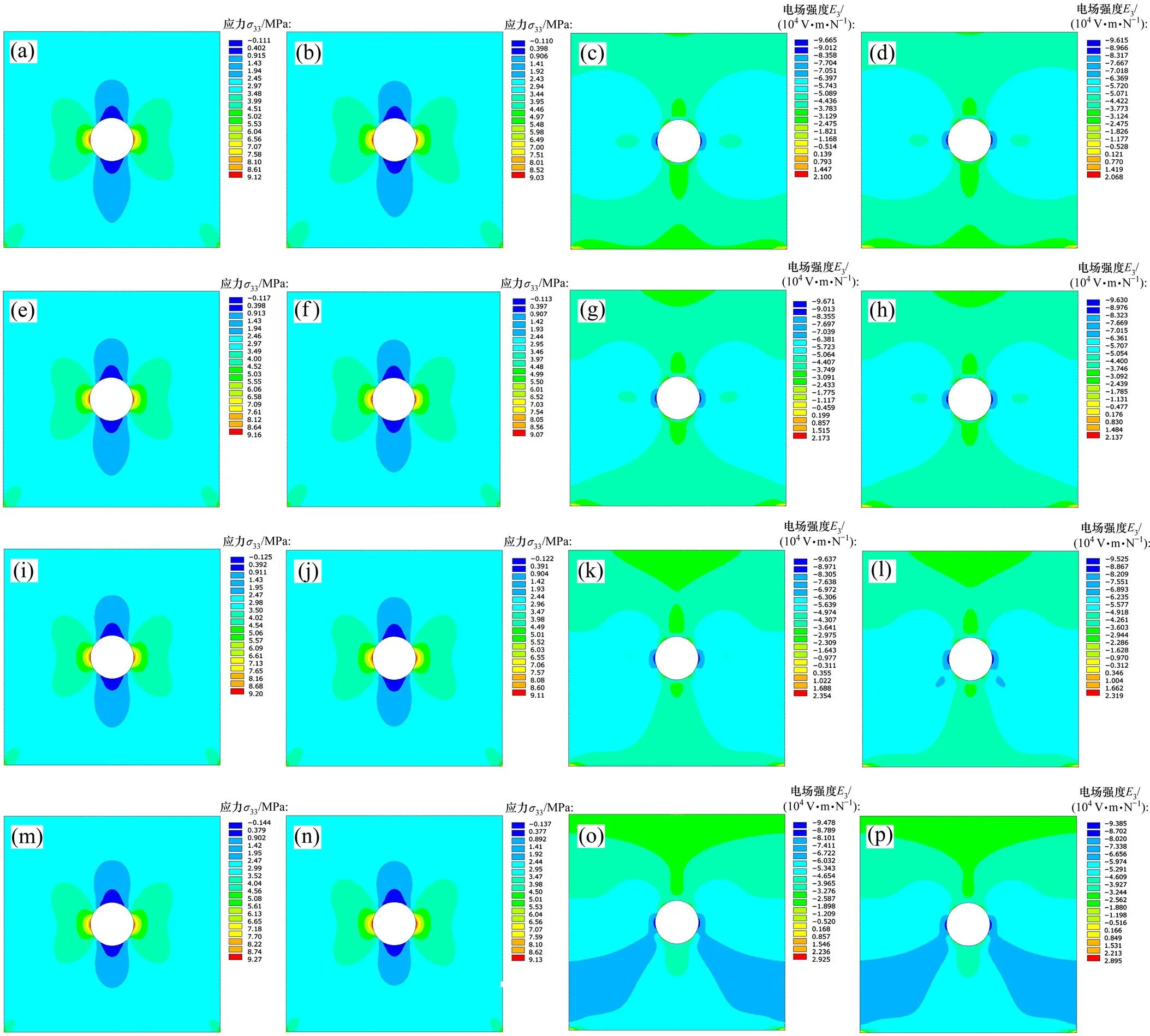
(a) 应力云图(SFEM，=0)；(b) 应力云图(FEM，=0)­­；(c) 电场强度云图(SFEM，=0)；(d) 电场强度云图(FEM，=0)；(e) 应力云图(SFEM，=0.2)；(f) 应力云图(FEM，=0.2)；(g) 电场强度云图(SFEM，=0.2)；(h) 电场强度云图(FEM，=0.2)；(i) 应力云图(SFEM，=0.5)；(j) 应力云图(FEM，=0.5)；(k) 电场强度云图(SFEM，=0.5)；(l) 电场强度云图(FEM，=0.5)；(m) 应力云图(SFEM，=1.0)；(n) 应力云图(FEM，=1.0)；(o) 电场强度云图(SFEM，=1.0)；(p) 电场强度云图(FEM，=1.0)

图5 不同梯度参数下功能梯度压电板（PZT−H5为底边）的应力云图和电场强度云图

Fig. 5 Stress contours and electric field contours of functionally graded piezoelectric plate(PZT−H5 as the base) with varied gradient parameters

4 结论

1) 非均匀基于单元的光滑有限元求解精度高于非均匀有限元求解精度，梯度光滑技术引入非均匀有限元中可改善非均匀有限元的系统刚度。

2) 当材料参数小梯度变化时，功能梯度压电板应力集中位置基本不变，应力对材料参数小梯度变化不敏感。

3) 当材料参数小梯度变化时，功能梯度压电板电场集中位置基本不变，电场强度对材料参数小梯度变化较敏感。

[1] SAADATFAR M. Effect of multiphysics conditions on the behavior of an exponentially graded smart cylindrical shell with imperfect bonding[J]. Meccanica, 2015, 50(8): 2135−2152.

[2] AREFI M. The effect of different functionalities of FGM and FGPM layers on free vibration analysis of the FG circular plates integrated with piezoelectric layers[J]. Smart Structures and Systems, 2015, 15(5): 1345−1362.

[3] WU C P, LIU Yancheng. A review of semi-analytical numerical methods for laminated composite and multilayered functionally graded elastic/piezoelectric plates and shells[J]. Composite Structures, 2016, 147: 1−15.

[4] NOURMOHAMMADI H, BEHJAT B. Design criteria for functionally graded piezoelectric plates under thermo-electro- mechanical loadings[J]. Journal of Intelligent Material Systems and Structures, 2016, 27(16): 2249−2260.

[5] MIKAEELI S, BEHJAT B. Three-dimensional analysis of thick functionally graded piezoelectric plate using EFG method[J]. Composite Structures, 2016, 154: 591−599.

[6] SELIM B A, ZHANG L W, LIEW K M. Active vibration control of FGM plates with piezoelectric layers based on Reddy’s higher-order shear deformation theory[J]. Composite Structures, 2016, 155: 118−134.

[7] ZHAO X, LEE Y Y, LIEW K M. Free vibration analysis of functionally graded plates using the kp-Ritz method[J]. Journal of Sound and Vibration, 2009, 319(3/4/5): 918−939.

[8] KOMIJANI M, REDDY J N, ESLAMI M R. Nonlinear analysis of microstructure-dependent functionally graded piezoelectric material actuators[J]. Journal of the Mechanics and Physics of Solids, 2014, 63: 214−227.

[9] DAI Yao, CHONG Xiao, LI Shimin. The higher order crack tip fields for anti-plane crack in functionally graded piezoelectric materials[J]. Applied Mechanics and Materials, 2014, 472: 617−620.

[10] JODAEI A. 3D elasticity solution for static analysis of functionally graded piezoelectric annular plates on elastic foundations using SSDQM[J]. Meccanica, 2014, 49(1): 215−237.

[11] RANGELOV T, DINEVA P, GROSS D. Effects of material inhomogeneity on the dynamic behavior of cracked piezoelectric solids: a BIEM approach[J]. Journal of Applied Mathematics and Mechanics, 2008, 88(2): 86−99.

[12] DINEVA P, GROSS D, MÜLLER R, et al. Time-harmonic crack problems in functionally graded piezoelectric solids via BIEM[J]. Engineering Fracture Mechanics, 2010, 77(7): 1101−1115.

[13] 孟广伟, 王晖, 周立明, 等. 含孔功能梯度压电材料板的力电耦合无网格伽辽金法[J]. 中南大学学报(自然科学版), 2015, 46(11): 4015−4020. MENG Guangwei, WANG Hui, ZHOU Liming et al. Electromechanical element-free Galerkin method for functionally graded piezoelectric plate with circular hole[J]. Journal of Central South University (Science and Technology), 2015, 46(11): 4015−4020.

[14] LIU Guirong, NGUYEN-THOI T, DAI K Y, et al. Theoretical aspects of the smoothed finite element method (SFEM)[J]. International Journal for Numerical Methods in Engineering, 2007, 71(8): 902−930.

[15] LIU Guirong, NGUYEN-THOI T, LAM K Y. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids[J]. Journal of Sound and Vibration, 2009, 320(4/5): 1100−1130.

[16] LIU Guirong, NGUYEN-XUAN H, NGUYEN-THOI T. A theoretical study on the smoothed FEM (S-FEM) models: Properties, accuracy and convergence rates[J]. International Journal for Numerical Methods in Engineering, 2010, 84(10): 1222−1256.

[17] NGUYEN-VAN H, MAI-DUY N, TRAN-CONG T. A node-based element for analysis of planar piezoelectric structures[J]. CMES: Computer Modeling in Engineering and Sciences, 2008, 36(1): 65−95.

[18] NGUYEN-XUAN H, LIU Guirong, NGUYEN-THOI T, et al. An edge-based smoothed finite element method for analysis of two-dimensional piezoelectric structures[J]. Smart Materials and Structures, 2009, 18(6): 065015.

[19] CHEN L, ZHANG Y W, LIU G R, et al. A stabilized finite element method for certified solution with bounds in static and frequency analyses of piezoelectric structures[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 241: 65−81.

(编辑 伍锦花)

Analysis of stress and electric field concentration in a functionally graded piezoelectric plate with a circular hole based on nonhomogeneous smoothed finite element method

CAI Bin1, ZHOU Liming2

(1. School of Civil Engineering, Jilin Jianzhu University, Changchun 130118, China;2. School of Mechanical Science and Engineering, Jilin University, Changchun 130025, China)

In order to improve the calculation precision of stress and electric field concentration factor for the functionally graded piezoelectric plate with a circular hole, electromechanical coupling nonhomogeneous cell-based smoothed finite element method was proposed. Real material properties of Gaussian point were used to calculate. Stress and electric field concentration factor of functionally graded piezoelectric plate with a hole was studied, in which material properties of the piezoelectric plate was changing exponentially in a certain direction. The results show that this method has high precision in calculating stress and electric field concentration factor for the functionally graded piezoelectric plate.

functionally graded piezoelectric materials; nonhomogeneous smoothed finite element method; stress field concentration factor; electric field concentration factor

10.11817/j.issn.1672-7207.2018.05.008

TB330.1；TB115

A

1672−7207(2018)05−1080−07

2017−05−17；

2017−06−27

国家自然科学基金资助项目(11502092)；吉林省科技计划项目(20160520064JH, 20170101043JC)；中央高校基本科研业务费专项资金资助项目(451170306066) (Project(11502092) supported by the National Natural Science Foundation of China; Projects (20160520064JH, 20170101043JC) supported by Scientific and Technology Program of Jilin Province; Project(451170306066) supported by the Fundamental Research Funds for the Central Universities)

周立明，博士，副教授，从事计算固体力学研究；E-mail: lmzhou@jlu.edu.cn