基于动态材料参数的5083铝合金本构模型

戴青松，邓运来，欧世声，付平



基于动态材料参数的5083铝合金本构模型

戴青松1，邓运来1，欧世声1，付平2

(1. 中南大学 材料科学与工程学院，湖南 长沙，410083；2. 广西柳州银海铝业股份有限公司，广西 柳州，545006)

通过热压缩试验研究5083铝合金在应变速率为0.01~10 s-1、变形温度为300~500 ℃、变形程度为50%条件下的流变行为，根据热模拟数据建立基于动态材料参数的双曲正弦函数本构模型(ZHCM)及幂函数本构模型(ZBCM)，并对这2种本构模型的应力预测精确度进行计算。研究结果表明：ZHCM与ZBCM均有较高的应力预测精度，应力平均相对误差分别为5.26%和3.92%，相比之下，ZHCM在应变速率为10 s−1、变形温度为300 ℃的条件下应力精度比ZBCM的高，而当应变速率为0.01~1 s−1、变形温度为350~500 ℃时，ZBCM的应力精度较高。

5083铝合金；热压缩；流变应力；动态材料参数；本构模型

在金属热加工过程中，材料流变应力因微观组织的变化而产生变化，流变应力将影响加工设备载荷与能耗，准确的流变应力本构模型(CM)可为加工设备的选型及载荷计算提供参考[1−6]。目前，表征金属热变形流变力学规律的本构模型主要有2种[7−9]：—种是幂函数和指数函数相结合，并包含了Zener−Hollomon参数的双曲正弦函数(ZH)；另一种是幂函数与指数函数相结合的Zuzin−Browman关系式(ZB)。这2种模型均涉及到材料参数的求解，为简化计算，这些参数通常被当作常数处理[10−11]，这种方式计算得出的本构模型可对峰值应力进行较精准预测，但若要建立可对整个变形过程进行精准预测的本构模型，还需考虑材料参数与热变形条件间的动态变化关系。一些学者在材料参数的修正与优化方面进行了很多研究，如：GAN等[12]在求解6063铝合金ZHCM时，考虑了材料参数与应变的关系；JIA等[13]在研究AZ31B镁合金本构方程时，考虑了材料参数的动态变化。本文作者以5083铝合金为研究对象，根据热压缩试验结果建立基于动态材料参数的ZHCM和ZBCM这2种本构模型，并结合实测数据对2种本构模型进行误差分析，以便为实际生产中设备选取与工艺制定提供参考。

1 试验材料与方法

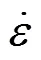
图1 热压缩试样金相组织

2 试验结果

图2所示为5083铝合金在不同变形条件下的真应力−真应变曲线。从图2可以看出：在热变形初期，5083铝合金真应力随着应变的增加迅速增大至峰值，当应力达到峰值以后，应变呈现稳态流变特征，甚至应力随应变的增加呈下降趋势。这是因为当应力达到峰值后，5083铝合金因动态回复、动态再结晶所引起的动态软化与位错引起的加工硬化处于动态平衡，甚至动态软化行为强于加工硬化，使材料呈现稳态流变特征，甚至呈现下降趋势[14−16]。由图2还可看出：在应变速率一定的情况下，5083铝合金流变应力随着变形温度的升高而明显下降。这是因为随着变形温度的升高，动态回复、动态再结晶引起的软化行为加剧，材料位错密度减小，因此，流变应力降低。而在变形温度一定的情况下，流变应力随着应变速率的增大而明显增大，这是因为当应变速率增大时，变形时间缩短，在较短的时间内动态软化行为来不及完全发生，位错数量明显增大，导致应力增大。

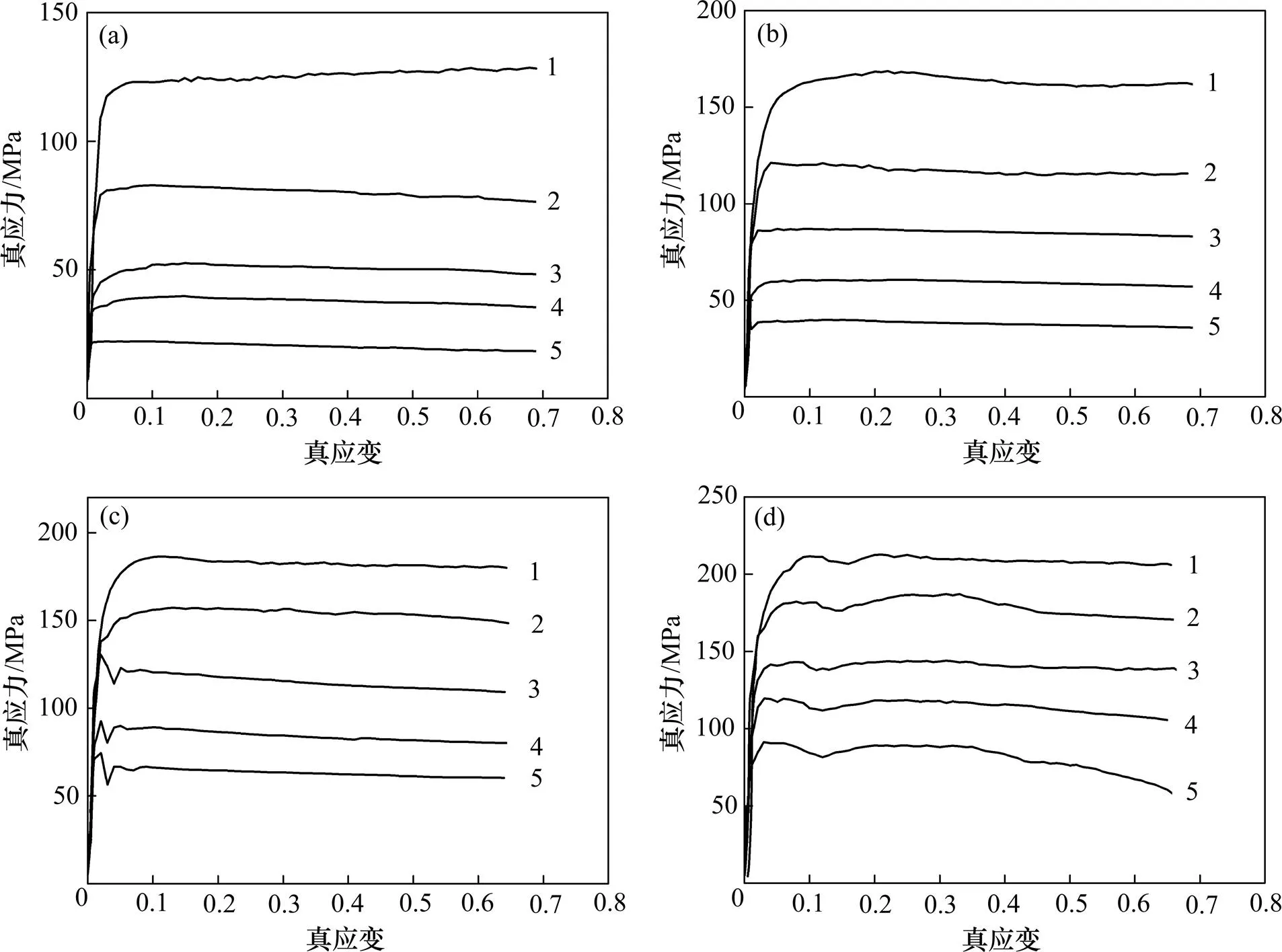
应变速率/s−1：(a) 0.01；(b) 0.1；(c) 1；(d) 10

3 分析与讨论

3.1 ZHCM的优化与求解

描述金属材料高温变形的双曲正弦函数本构模型表达式如下[17−20]。

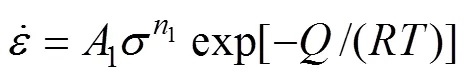
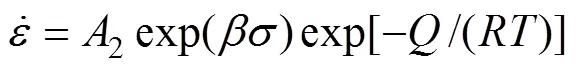
在整个应力范围内，

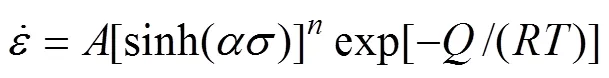
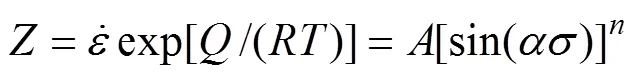
对式(1)~(3)取对数并求偏微分可得：

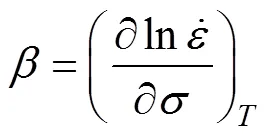
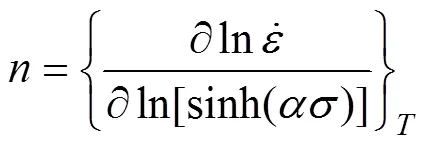
对式(3)和式(4)取自然对数并求偏导可得：

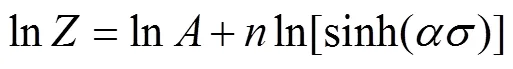
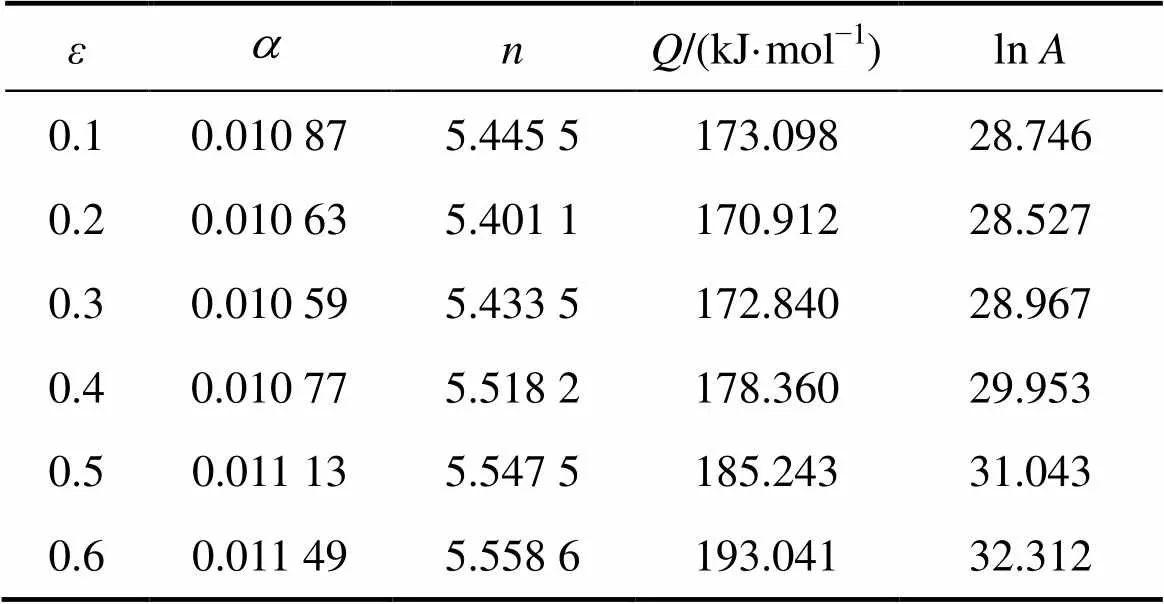
表1 5083铝合金各参数值

由图3中各参数曲线的拟合结果，可求得基于动态材料参数的5083铝合金ZHCM为

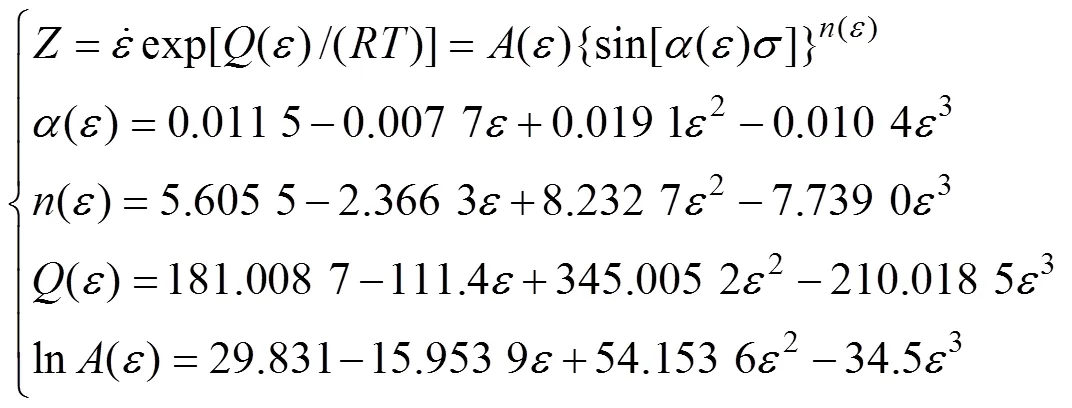
3.2 ZBCM的优化与求解

材料高温流变应力与变形条件间的关系可采用幂函表示[7, 13]：

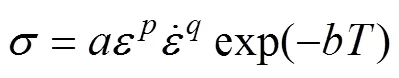
式中：，，和分别表示材料参数、应变硬化指数应变速率敏感系数和温度系数。

图3 材料参数与的关系

Fig. 3 Relationship between material parameters and

对式(11)取自然对数后求偏微分可求得，和与各变形条件的关系：

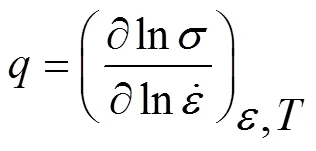
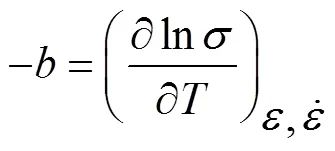
根据热压缩试验数据及式(12)~(14)可分别求得不同应变速率、不同变形温度下的，不同真应变、不同变形温度下的，不同真应变、不同应变速率下的。通过，和可反求出不同应变速率、不同变形温度下的，计算结果如图4和图5所示。

由图4可知：不同变形条件下的和具有明显收敛至某一常数的特征，为简化计算，可认为和为常数，对其求平均值可得：=−0.033 1，=−0.138 6。

由图5可知：式(11)中的和均随着应变速率的变化而明显变化，若将和看成常数将影响到本构模型的应力精度，因此，建立和与应变速率的动态关系。

(a) p；(b) q

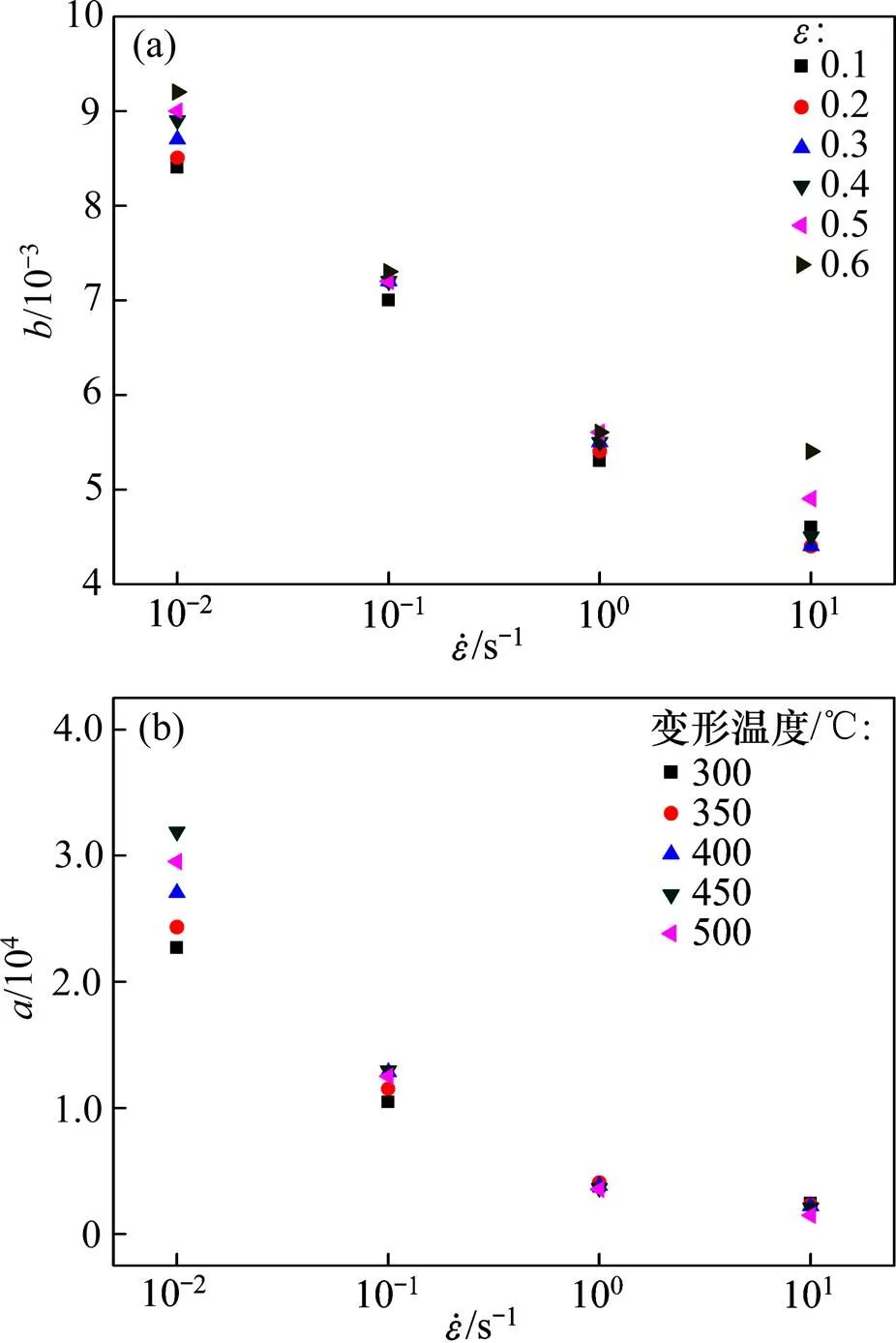
(a) b；(a) a

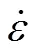
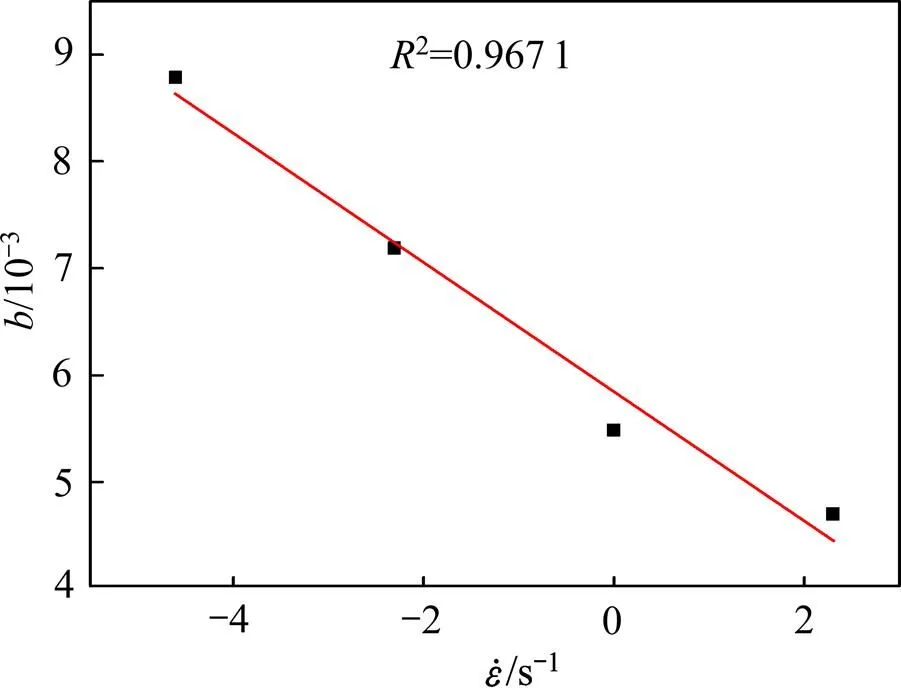
图6 5083铝合金的b与的关系

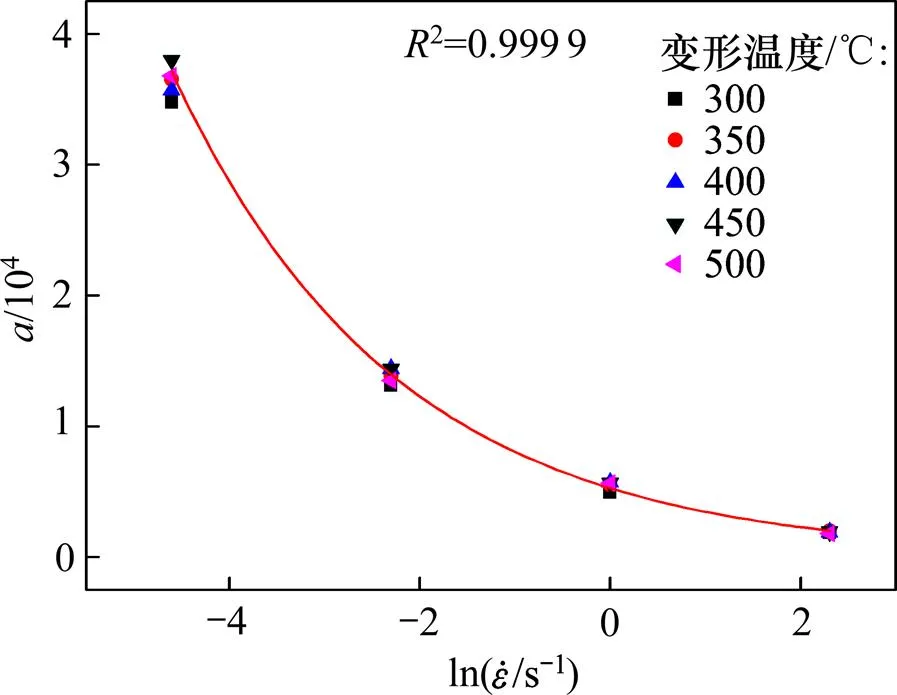
图7 5083铝合金的a与的关系

由以上分析可知，式(11)可表示为

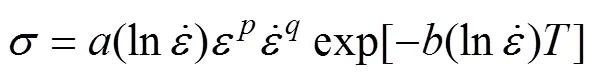
根据图6和图7的曲线拟合结果，可求得基于动态参数的5083铝合金ZBCM为

3.3 误差分析与对比

图8所示为不同变形条件下实测流变应力与2种优化本构模型计算值的对比情况。由图8可以看出：2种本构模型应力计算值都与实测值接近，说明2种模型都较准确。为更清晰地评价应力计算值与实测值之间的相对误差，将图8中数据代入式(17)和式(18)进行相对误差计算。通过计算发现，ZHCM的平均相对误差为5.26%，ZBCM的应力平均相对误差为3.92%，ZBCM的应力精准度相对更高。

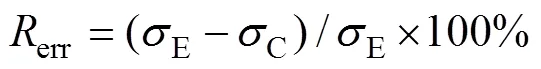
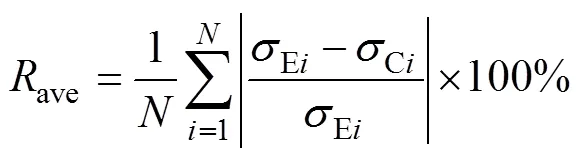
进一步计算同一温度、同一应变量、不同应变速率下应力的相对误差平均值，对比分析各变形温度、应变量下应力的相对误差，计算结果如图9(a)所示。由图9(a)可知：当变形温度为300 ℃时，ZHCM的应力平均相对误差为3.89%，整体上小于ZBCM的4.55%；而当变形温度为350~500 ℃时，ZHCM的应力平均相对误差为5.66%，大于ZBCM的3.64%。计算同一应变速率、同一应变量、不同温度下的应力相对误差平均值，对比分析各应变速率、应变量下的应力相对误差，计算结果如图9(b)所示。由图9(b)可知：当应变速率为0.01~1 s−1时，ZBCM的应力相对误差均比ZHCM的小，其应力平均相对误差仅为3.33%；而当应变速率为10 s−1时，ZHCM的应力平均相对误差为2.59%，小于ZBCM的5.68%。对比分析可知，ZHCM在低温、较高应变速率下的应力精度比ZBCM的高，而ZBCM在较高温度、低应变速率下具有更高的应力精度，根据图2的流变曲线可知，流变应力随着温度的降低或应变速率的增大而增大，因此，说明ZHCM更适合高应力条件，ZBCM更适合低应力条件。本文ZHCM方程中建立了材料参数与应变的关系，而ZBCM方程建立了材料参数与应变速率的关系，材料参数与变形条件的关系可能是造成2种方程优选适用范围不同的原因。材料试样平均晶粒粒径为50 μm，晶粒相对较小，应力水平较高，ZHCM方程材料参数随应变变化而变化，更能对高应力条件进行预测，因此，ZBCM在高应力水平条件下的应力预测精度比ZHCM的精度低，而在低水平应力条件下应力预测精度比ZHCM的精度高。

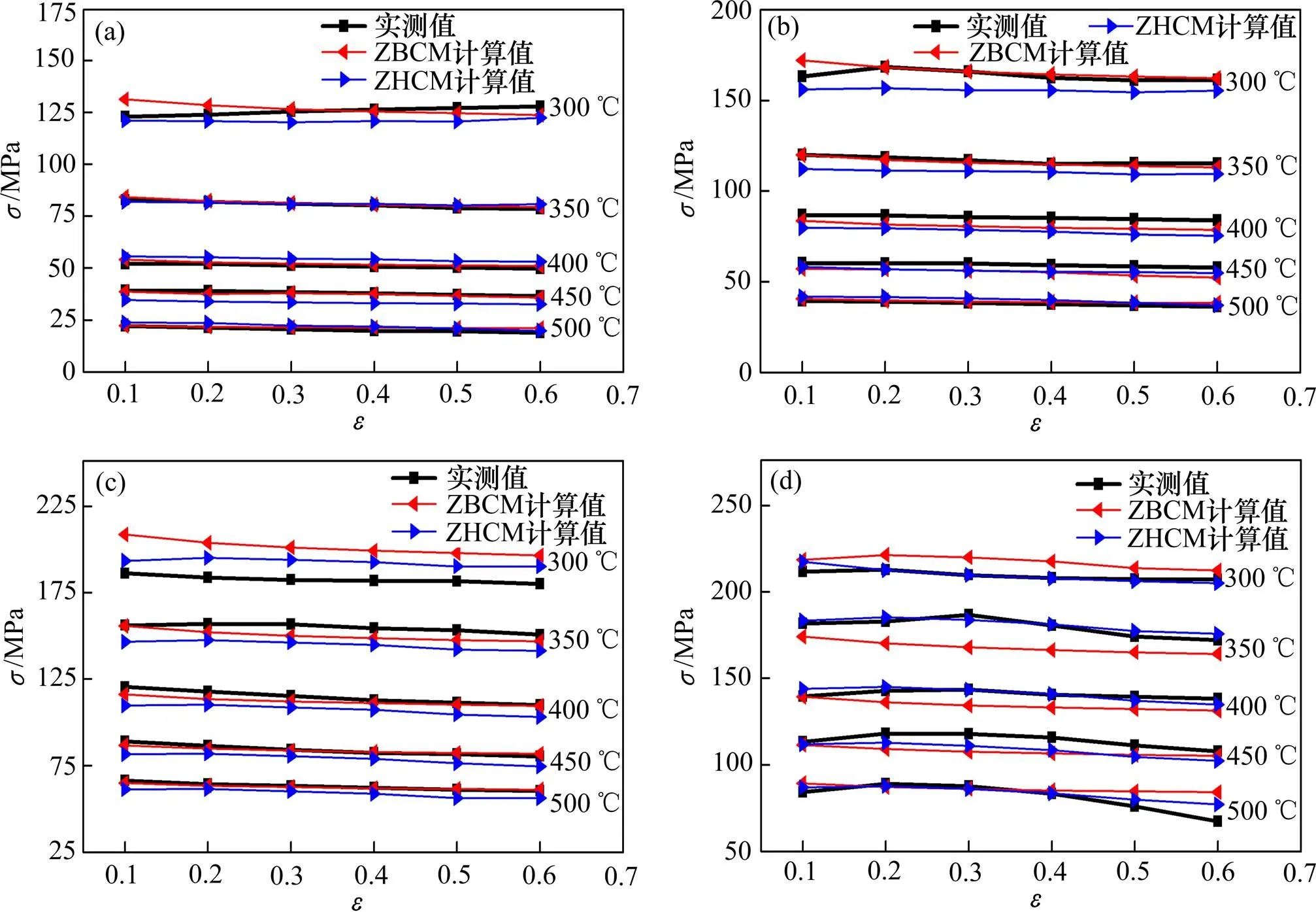
/s−1：(a) 0.01；(b) 0.1；(c) 1；(d) 10

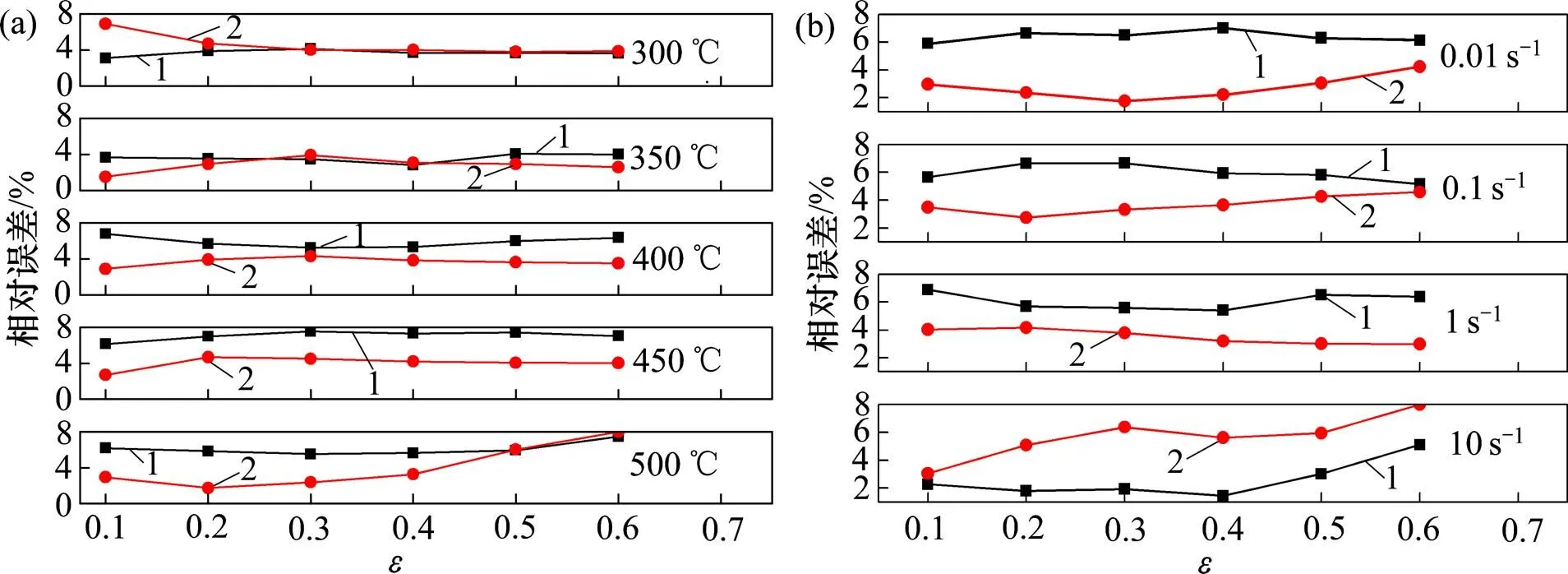
(a) 不同变形温度；(b) 不同应变速率

4 结论

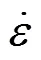
[1] VILAMOSA V, CLAUSEN A H, BØRVIK T, et al. A physically-based constitutive model applied to AA6082 aluminium alloy at large strains high strain rates and elevated temperatures[J]. Materials and Design, 2016, 103: 391−405.

[2] YANG Qunying, YANG Dong, ZHANG Zhiqing, et al. Flow behavior and microstructure evolution of 6A82 aluminium alloy with high copper content during hot compression deformation at elevated temperatures[J]. Transactions of Nonferrous Metals Society China, 2016, 26(3): 649−657.

[3] WU Hongdan, ZHANG Hui, CHEN Shuang, et al. Flow stress behavior and processing map of extruded 7075AlSiC particle reinforced composite prepared by spray deposition during hot compression[J]. Transactions of Nonferrous Metals Society China, 2015, 25(3): 692−698.

[4] ZHANG Jiangtao, XIA Junkang, ZHANG Mei, et al. Tensile fracture mechanism and constitutive models of V-5Cr-5Ti alloy under different strain rate deformation at room temperature[J]. Materials Letters, 2016, 183: 40−43.

[5] 李军, 于辉, 史庆南, 等. 纯钛高温变形行为及其在精轧板中的应用[J]. 中南大学学报(自然科学版), 2016, 47(6): 1888−1895. LI Jun, YU Hui, SHI Qingnan, et al. Hot deformation behavior of pure titanium and its application in hot sheet finish rolling[J]. Journal of Central South University (Science and Technology), 2016, 47(6): 1888−1895.

[6] 丁汉林, 徐成志, 张晓军, 等. ZX115镁合金热压缩过程的本构分析及有限元模拟[J]. 中国有色金属学报, 2015, 25(8): 2075−2082. DING Hanlin, XU Chengzhi, ZHANG Xiaojun, et al. Constitutive analysis and FEM simulation of hot compression of ZX115 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(8): 2075−2082.

[7] 于鑫, 孙杰, 熊青春, 等. 7050-T7451铝合金铣削加工表面材料特性与本构关系模型的建立[J]. 中国有色金属学报, 2015, 25(11): 2982−2989. YU Xin, SUN Jie, XIONG Qingchun, et al. Milling surface properties of 7050-T7451 aluminum alloy and establishment of constitutive model[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(11): 2982−2989.

[8] XIAO Gang, YANG Qinwen, LI Luoxing, et al. Modeling constitutive relationship of 6013 aluminum alloy during hot plane strain compression based on Kriging method[J]. Transactions of Nonferrous Metals Society China, 2016, 26(4): 1096−1104.

[9] 邓馗, 李永堂, 付建华, 等. 铸态P91耐热合金钢高温流变行为及本构方程[J]. 锻压技术, 2015, 40(11): 100−106. DENG Kui, LI Yongtang, FU Jianhua, et al. High temperature rheological behavior and constitutive equation of as-cast heat-resisting alloy steel P91[J]. Forging Stamping Technology, 2015, 40(11): 100−106.

[10] ZHU Ruihua, LIU Qing, LI Jinfeng, et al. Dynamic restoration mechanism and physically based constitutive model of 2050 Al-Li alloy during hot compression[J]. Journal of Alloys and Compounds, 2015, 650: 75−85.

[11] 杨春秀, 陈忠平, 李华清, 等. 铝青铜合金热变形流变应力特征[J]. 稀有金属材料与工程, 2010, 39(Suppl 1): 126−129. YANG Chunxiu, CHEN Zhongping, LI Huaqing, et al. Flow stress feature of aluminium bronze alloy under hot deformation[J]. Rare Metal Materials and Engineering, 2010, 39(Suppl 1): 126−129.

[12] GAN Chunlei, ZHENG Kaihong, QI Wenjun, et al. Constitutive equations for high temperature flow stress prediction of 6063 Al alloy considering compensation of strain[J]. Transactions of Nonferrous Metals Society China, 2014, 24(11): 3486−3491.

[13] JIA Weitao, XU Shuang, LE Qichi, et al. Modified Fields-Backofen model for constitutive behavior of as-cast AZ31B magnesium alloy during hot deformation[J]. Materials and Design, 2016, 106: 120−132.

[14] PARK S Y, KIM W J. Difference in the hot compressive behavior and processing maps between the as-cast and homogenized Al-Zn-Mg-Cu (7075) alloys[J]. Journal of Materials Science & Technology, 2016, 32(7): 660−670.

[15] WU H, WEN S P, HUANG H, et al. Hot deformation behavior and processing map of a new type Al-Zn-Mg-Er-Zr alloy[J]. Journal of Alloys and Compounds, 2016, 685: 869−880.

[16] HESAM P, MEHDI P, SOHEIL F, et al. Study on the dynamic and static softening phenomena in Al-6Mg alloy during two-stage deformation through interrupted hot compression test[J]. Measurement, 2016, 77: 50−53.

[17] 陈宝东，郭锋，温静，等. Mg-Zn-Zr-Y合金高温塑性变形本构模型及流变行为预测[J]. 稀有金属材料与工程, 2017, 46(11): 3305−3310.

CHEN Baodong, GUO Feng, WEN Jing, et al. Constitutive model of hot plastic deformation and flow behavior prediction of Mg-Zn-Zr-Y alloy[J]. Rare Metal Materials and Engineering, 2017, 46(11): 3305−3310.

[18] 付平，刘栩，戴青松，等. 5083铝合金热压缩流变应力曲线修正与本构方程[J]. 材料工程, 2017, 45(8): 76−82.

FU Ping, LIU Xu, DAI Qingsong, et al. Modification of flow stress curves and constitutive equations during hot compression deformation of 5083 aluminum alloy[J]. Journal of Materials Engineering, 2017, 45(8): 76−82.

[19] ZHU Shaozhen, LUO Tianjiao, ZHANG Tingan, et al. Hot deformation behavior and processing maps of as-cast Mg-8Zn-1Al-0.5Cu-0.5Mn alloy[J]. Transactions of Nonferrous Metals Society China, 2015, 25(10): 3232−3239.

[20] XU Zhaohua, LI Miaoquan, LI Hong, et al. Plastic flow behavior of superalloy GH696 during hot deformation[J]. Transactions of Nonferrous Metals Society China, 2016, 26(3): 712−721.

(编辑 刘锦伟)

Constitutive model of 5083 aluminum alloy based on dynamic material parameters

DAI Qingsong1, DENG Yunlai1, OU Shisheng1, FU Ping2

(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;2. Guangxi Liuzhou Yinhai Aluminum Co. Ltd., Liuzhou 545006, China)

The flow stress features of 5083 aluminum alloy were investigated by the isothermal compression test at the strain rates of 0.01−10 s−1, the temperatures of 300−500 ℃ and the deformation degree of 50%. According to the thermal simulation data, the hyperbolic sine constitutive model (ZHCM) and power function constitutive model (ZBCM) were established based on the dynamic material parameters. Furthermore, the stress prediction accuracies of two constitutive models were calculated. The results show that both ZHCM and ZBCM have high stress precision of prediction, and the average relative errors of stress are 5.26% and 3.92%, respectively. By contrast, the ZHCM has higher stress accuracy at the strain rate of 10 s−1and the deformation temperature of 300 ℃, while the stress accuracy of ZBCM predicts more accurately at the strain rate of 0.01−1 s−1and the deformation temperature of 350−500 ℃.

5083 aluminum alloy; hot compression; flow stress; dynamic material parameter; constitutive model

10.11817/j.issn.1672-7207.2018.05.007

TG146.2

A

1672−7207(2018)05−1072−08

2017−05−15；

2017−07−03

广西科学研究与技术开发计划项目(1598001-2，14122001-5) (Projects(1598001-2, 14122001-5) supported by the Scientific Research and Technology Development Program of Guangxi)

邓运来，教授，博士生导师，从事有色金属材料加工工程研究；E-mail: luckdeng@csu.edu.cn