低年级学生“对应思考”背后的迷思现象剖析

王冬秀

【摘要】本文分析学生出现“对应思考”背后的迷思现象，指出其错误的原因是学生特有的思考方式与正式的数学概念相混淆，并将这些错误进行归类，探寻错误背后蕴含的认知规律，找到改进的方向。

【关键词】小学数学 概念迷思 对应思考 错因

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2018）03A-0060-02

在小学数学学习过程中，不可规避的一个思维要素，那就是对应思考。如将三百二十五写成325，这是对数的汉语表达和数字表达进行对应的转换，这就是一个对应的思考。计算中需要对参与运算的数进行对应思考，在解决文字应用题时，也需要对文字信息和算式之间进行对应思考。然而，笔者发现学生经常会根据自身的理解展开对应思考，由此产生了一些认知误区。有基于此，笔者将其归类，以期帮助同仁根据学生的这些认知错误，找到学生错误产生的原因，进而找到改进的方向。

一、語言与数字转换中的对应迷思

在数学学习中，语言和数字之间有一个对应的关系，学生在思考这两种关系时，头脑中已经有一种自己的直觉理解。这种直觉理解将会成为学生对应思考中的线索，学生会不知不觉地沿着这条线索走下去，无意识中走入歧途，形成对应迷思。例如，在学习“多位数读写”中要求学生写出四百三十二万零六十五时，学生往往写成432065。为什么会这样呢？因为学生在直觉理解中有一个思维定势：即将四百三十二万零六十五看成是由“四百三十二”“零”和“六十五”这三个元素构成的，而且这三个要素是按照顺序排列的，只要将这三个要素翻译为数字432，0和65，然后根据原有顺序排列就可以得到问题的答案。另外，由于一一对应的迷思产生的理解错误，还会导致数量错误。如学生在初次学习钟表时，会将钟面上直观显示的时针指向11，分针指向2，读作或写作11：02；将时针指向9，分针指向6，读作或者是写作9：06，这种错误来自视觉上意义相同的对应误解。

可见，在小学数学课程内容中，文字、图形和符号在学习过程中需要进行转换，转换时一旦出现了意义、顺序或数量的改变，学生的这种直觉理解容易产生误解和认知错误，为其思考带来极大的困扰。

二、加减计算中的对应迷思

对于低年级学生来说，加减法计算看似简单，但往往会出现诸多错误。教师通常将这些错误当作是学生马虎、不细心造成的，其实并非如此，大部分是出现一些对应迷思。如在计算523+25时，学生就出现了如下的错误做法：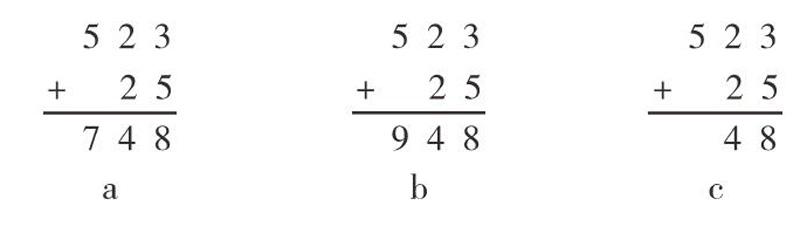

大部分教师会认为这样的计算没有出现进位，难度很小，学生是不会出错的。但事实上，在加法竖式计算中，笔者经过多次验证后发现，没有进位的加法计算学生更容易出错。原因在哪呢？其实，在学生的加法计算经验中，存在着这样的对应理解：一是加法应该至少有两个数才能够进行计算，一个数不能做加法。二是两个加数的各个数位上的数字必须是一一对应的。正因为有了这样的理解，学生在面对523+25这一竖式计算时，对个位上和十位上的数字3+5，2+2都能够顺利完成，但是对于孤立存在的百位上的5，就不知道该怎么做了。因为学生在潜意识中存在着加法一定是需要两个加数这样的迷思，所以就会在计算过程中寻找能够和5做加法的数，按照就近的原则，就可能会用到临近的数字2，这样就得到了523+25等于748，也有可能会用到临近的数字4，这样就得到523+25=948。而对于有进位的加法计算题593+25，恰恰与学生头脑中加法需要两个加数的想法吻合，因此就可以顺利地完成百位数上5+1等于6这个计算，错误率比523+25更低。在实践中笔者发现，这种对应迷思在减法计算中也会出现，例如276-14，学生看到百位数上出现了一个孤立的2，就会认为需要再寻找一个减数与它对应，所以会选择临近的数字实现和2的减法计算，最终得到一个错误的结果162。

可见，学生在潜意识中存在的错误迷思，使加减法计算产生了误区，要提高学生的思维能力，就要清除学生的对应迷思。

三、文字应用题中的对应迷思

在小学低年级数学学习中，文字应用题是一个重要的内容，也是考查学生思维的关键内容。这部分内容学生的对应思考也容易出现迷思，这些迷思具有普遍性，给学生解决问题造成了极大的困扰。例如，树上有一些小鸟，飞走了5只，还剩下23只，树上原来有多少只小鸟？这道文字应用题数量关系并不复杂，教师原以为学生能够列出算式5+23，但事实上，大部分学生都是直接写出算式和结果28-5=23。原因在哪呢？其实这道文字题本身的描述在学生头脑中形成的是这样的一个结构：树上有一些小鸟→飞走5→还剩23。值得注意的是，在这个结构中有三个要素，它们是按照时间的先后顺序自然排列的。根据这样的要素排列结构，学生心算得出共有28只。另外在学生的经验中还有这样的理解：“飞走”就是对应一个减号，“还剩”对应的就是一个等号，由此学生根据一一对应的关系，写出了算式28-5=23（只）。而教师所期望的5+23=28这种计算方法，打乱了学生一一对应的思考步骤，造成了学生的困扰。在学生的经验中，飞走和还剩都应该与减法直接相关。而且在这道文字应用问题中，情境的设置里并没有发生和加法有关的过程，所以学生自然而然想到的就是写出一个减法算式。另外，在这道文字应用题中的结构违背了要素之间原有的顺序，在学生原有的经验认知中，是按照情景实际发生的顺序来书写算式，而教师所期望的算法、写法顺序与文字叙述的顺序是不同的，打破了学生直观经验中对结构顺序的认知。在这个结构要素中，计算顺序是被打乱的，而学生的经验是按照实际发生的顺序来进行，这就与教师所期望的计算顺序相违背。从这个意义上说，学生出现这样的写法也就不足为奇了。

总之，教师要认真地思考学生的思维迷思，从而读懂学生，为下一步发展学生的思维打好基础。

（责编 林 剑）