考虑裂纹影响的海洋管道极限弯曲载荷分析
,,
(1.北京石油化工学院 机械工程学院,北京 102617;2.中国石油大学(北京) 海洋油气研究中心,北京 102249)①
管道在卷管铺设过程中受到随机载荷、冷弯、地面运动等作用,不可避免地发生了塑性变形。管道上卷时受到的弯曲载荷较大,塑性变形也较大。如果没有准确预估弯曲载荷的大小,海管在上卷过程中很可能会因局部的压溃,甚至断裂而造成整根海管失效。尤其是对于焊接中产生的裂纹,如图1所示,在弯曲载荷作用下裂纹逐渐变大,且截面发生了椭圆化变形,使裂纹迅速扩展,从而使得海管失效速度加快。
裂纹会对海管的极限弯曲载荷产生一定的影响,准确预估海管的极限弯曲载荷对保证海管安全运行有重要的意义。

图1 含有裂纹的海管受到弯曲载荷作用发生变形
对含有裂纹的管道进行极限弯曲载荷研究,最早的是Miller[1]和Zahoor[2],他们分别提出了含有裂纹管道的极限弯曲载荷表达式,被后来的很多学者引用,并以此为基础对裂纹问题做进一步的探讨和研究。其中,Chattopadhyay对含裂纹的管道研究的较多,包括用试验和解析方法研究含裂纹管道的三点弯曲问题、含纵向裂纹的管道受到面内弯矩作用的塑性压溃问题、含周向裂纹的管道受到面内弯矩和内压联合作用的压溃问题等[3-8]。Yahiaooui等总结了最近几年关于含有纵向和周向裂纹的碳钢管道受到弯曲载荷作用的试验和有限元模拟的研究,并对这些研究成果做了比较,指出以前研究人员计算得到的数据较为保守,可为实际工程提供参考[9]。Lei在文献[10]中提出了关于含有轴向裂纹的厚壁筒受到内压作用时的极限载荷求解方法,用这种方法求解的结果与有限元计算结果吻合良好。在国内,对含有裂纹的管道的研究也较多。帅健等给出了基于J积分理论的含裂纹管道的失效评定曲线的基本方程,并用有限元方法计算裂纹管道的J积分[11]。韩克江等针对现有的断裂力学方法应用于管道大范围屈服断裂评估的局限性,分别从双参数断裂力学、基于约束校正的断裂韧性测试、基于应变的断裂评估和基于应变的失效评估4个方面详细地介绍了管道大范围屈服断裂评估的研究现状,指出目前基于约束校正的管道断裂韧性测试的主要方法是用SENT试件方法和表观断裂韧性方法[12]。周晶等分析了海底管线全寿命安全运行的关键问题[13]。金伟良等介绍了结构失效评估图(FAD)技术,详细阐述了BS7910:1999规范中3个不同等级的断裂评估方法和疲劳评估方法[14]。对于卷管铺设方法中所使用的海管,Netto等研究了其疲劳寿命评估方法[15],并在文献[16]中研究了含有环向焊缝且有预应力的管道的疲劳问题。Tkaczyk等研究了受循环弯曲载荷作用的管道的疲劳寿命评估[17],并在文献[18]中研究了带有屈服平台的管道材料的非线性断裂评估方法。
综合以上研究内容,关于含有裂纹管道的研究较多,但大多集中在关于裂纹扩展、疲劳裂纹研究等问题,而对于含裂纹且有初始弯曲曲率的管道受弯曲载荷作用的研究较少。本文针对该问题进行了研究,首先总结已有的无裂纹管道的极限弯曲载荷表达式,并简述其适用范围,包括本文所推导的无裂纹管道的极限弯曲载荷表达式。然后,列出已有的比较有代表性的含裂纹的管道的极限弯曲载荷表达式。本文用有限元软件ABAQUS模拟有初始裂纹且有初始弯曲曲率的海管受弯曲载荷作用的多种工况,并将计算结果与已有的表达式结果进行比较,得出本文的有关含有初始裂纹的弯曲海管的极限弯曲载荷表达式,并对其影响因素做了进一步探讨。
1 极限弯曲载荷理论
有裂纹的海管受到弯曲载荷作用后,将会有拉伸应力(e-f弧线)和压缩应力(c-d弧线)产生,如图1所示。这种拉伸和压缩应力使海管的截面发生椭圆化变形,而裂纹在cd弧线段上面,若裂纹尺寸小于cd弧线尺寸,则裂纹也是在受压的一侧,且不会张开,在海管弯曲成一定曲率之前不会影响海管的稳定性。反之,裂纹将会使极限弯曲载荷发生变化,会对海管的稳定性产生一定的影响,这与无裂纹海管的极限弯曲载荷有一定关系。
1.1 无裂纹海管的极限弯曲载荷理论
海管在受到弯曲载荷作用时,其极限弯曲载荷即为海管塑性失稳或者局部压溃的载荷,塑性失稳载荷的特点为载荷单调增加时的最大载荷,在该处海管发生了塑性变形。对于极限弯曲载荷的计算方法,在很多文献中都有涉及,文献[19]中提出含有初始弯曲曲率的管道的极限弯曲载荷为:
(1)
h=tRb/R2
(2)
式中:σy为管道的屈服强度;h为管道弯曲性质参数;Rb为管道的弯曲半径;R为管道平均半径;D为管道外径;t为管道壁厚。
Calladine在文献[20]中得出含有初始弯曲曲率的管道的极限弯曲载荷为:
(3)
以上2个表达式均基于小变形分析,且管道材料均假设为理想弹性模型。对于大变形分析,Goodall在文献[21]中提出了另外一种表达形式,即:
(4)
其中:
(5)
式中:ν为泊松比;E为弹性模量。
Touboul基于实验提出了塑性压溃的2种弯矩表达式[22]。
对于图2,极限弯曲载荷表达式为:
M0=0.715h2/3(4R2tσy)
(6)
对于图3,极限弯曲载荷表达式为:
M0=0.722h1/3(4R2tσy)
(7)

图2 受正向弯曲载荷作用的海管

图3 受反向弯曲载荷作用的海管
本文在文献[23]基础上提出了含有初始弯曲曲率海管的极限弯曲载荷表达式为:
(8)
式中:Δ为椭圆度;k为管道弯曲曲率;t为壁厚;r为管道弯曲半径;k0为初始弯曲曲率。
(9)
然而,对于含有初始裂纹的海管,无法用上面的式子进行计算。故需要对含有裂纹的海管进行分析和研究。
1.2 有裂纹海管极限弯曲的载荷理论
含裂纹的截面的弯矩可由式(10)求得。
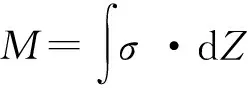
(10)
式中:M为弯矩;σ为局部应力;Z为含裂纹的截面模量。
随着加载弯矩的逐渐变大,局部应力σ随着管道材料的硬化也在逐渐发生变化,其值与加载方式有关。
对于含有裂纹和初始弯曲曲率的管道的极限弯曲载荷,Miller和Zahoor最先提出了各自的弯曲载荷表达式,并被后来的学者们作为研究的基础和参考。
针对管道部分周向贯穿裂纹,Miller[1]提出的极限弯曲载荷表达式为:
(11)
M0=0.935(4R2tσf)h2/3
(12)
h=tRb/R2
(13)
式中:3θ为总的周向裂纹角。
针对部分周向贯穿裂纹,Zahoor[2]提出的极限弯曲载荷表达式为:
(14)
式(14)适用于:
(15)
式中:a为裂纹长度的一半;Dm为管道的平均弯曲半径。
Zahoor还提出了含有纵向贯穿裂纹的极限弯曲载荷表达式。
(16)
然而,这些公式并没有区分弯曲载荷的施加方式(如图2和图3)。式(8)是基于其施加方式的不同,并考虑海管在变形中截面发生了椭圆化变形而进行推导的,本文将基于此,对含有裂纹的海管的极限弯曲载荷做进一步的研究。假设:
ML=M0X
(17)
其中,M0由式(8)得。X可通过后面的有限元模拟计算,并对计算结果进行拟合得出。
2 有限元计算分析
本文对卷管铺设过程中的海管采用大型通用非线性有限元软件ABAQUS进行数值模拟。海管外径219 mm,壁厚12 mm,长度为40 mm,初始弯曲曲率为-0.01 m-1,即,施加弯矩并使海管的弯曲曲率与初始的弯曲曲率方向相反,海管的部分周向贯穿裂纹角的一半为π/16,材料参数选取X65钢。在Assembly模块中通过划分实体,得到所要的初始裂纹的形状,在Interaction模块里Special-Crack-Assign Seam定义初始裂纹。对裂纹附近区域划分了较为密集的网格,如图4所示。在模拟中,施加位移载荷来控制海管的变形,不考虑裂纹的扩展。当局部塑性应变达到一定程度,即可判定海管失稳,计算结果如图5所示。
从图5的海管变形图中可以看出,裂纹处海管发生的变形最大,且有应力集中现象。随着弯矩载荷的变大,裂纹处最先发生局部失稳,故裂纹对海管的极限弯矩载荷有较大影响。

图4 海管有限元模型

图5 管道塑性应变累计分布
本文建立了裂纹半角为π/16、π/8、3π/16、π/4、5π/16、3π/8、7π/16、π/2的有限元模型,并分别进行计算。表1列出了式(11)、式(14)的计算结果,以及本文所做的有限元计算结果,并将计算结果绘制在图6中。

表1 含裂纹海管的极限弯矩载荷计算结果
注:1) 裂纹半角为π/16、π/8、3π/16等。
2)ML为含裂纹管道极限弯曲载荷。
3)M0为无裂纹管道极限弯曲载荷。
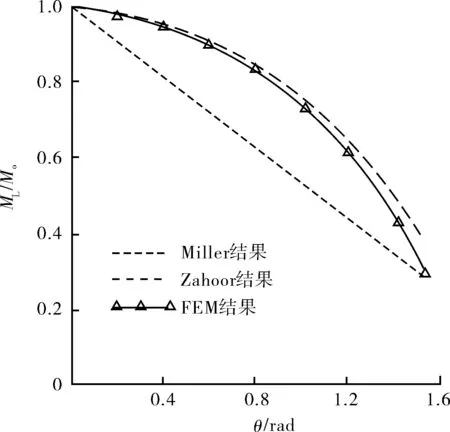
图6 极限弯曲载荷与裂纹角度对应关系
从图6中可看出,3种方法得到的计算结果均表明,随着裂纹角的增大,极限弯曲载荷逐渐减小。Zahoor结果与有限元计算结果略高于Miller结果。当裂纹角超过π/2后,有限元计算结果将迅速减小,这主要是由于海管局部发生失稳,极限弯曲载荷会迅速减小。有限元计算结果与实际的海管变形情况更加接近,其可靠度更高一些。对有限元计算结果进行拟合,得出:
(18)
从式(18)可看出,有裂纹海管的极限弯曲载荷与裂纹角有关,且和无裂纹海管的极限弯曲载荷有关。无裂纹海管的极限弯曲载荷又受海管管径、壁厚、初始弯曲曲率等参数的影响。故有裂纹海管的极限弯曲载荷也与管径、壁厚、初始弯曲曲率有关。
3 影响弯曲载荷变化的主要因素
针对式(18),分析有裂纹海管的极限弯曲载荷随影响因素变化的规律时,首先求出无裂纹海管的极限弯曲载荷,这主要通过式(8)和式(9)求得。海管几何参数的变化主要是管外径和壁厚的变化,本计算中固定海管管径为219 mm,只对壁厚的变化进行研究。除了海管的几何参数外,海管的初始弯曲曲率也对海管的极限弯曲载荷产生影响,故对海管的初始弯曲曲率进行研究,负值表示海管加载时海管产生弯曲曲率的方向与海管最初的弯曲曲率方向相反,正值表示相同(例如图2与图3)。对t=12、14、16、18 mm,和k0=-0.01、-0.02、-0.03、-0.04、0.01、0.02、0.03、0.04 m-1分别进行了计算,计算工况如表2所示。表3列出了无裂纹海管的极限弯曲载荷值,并将这些数据用Origin软件进行绘图,如图7所示。
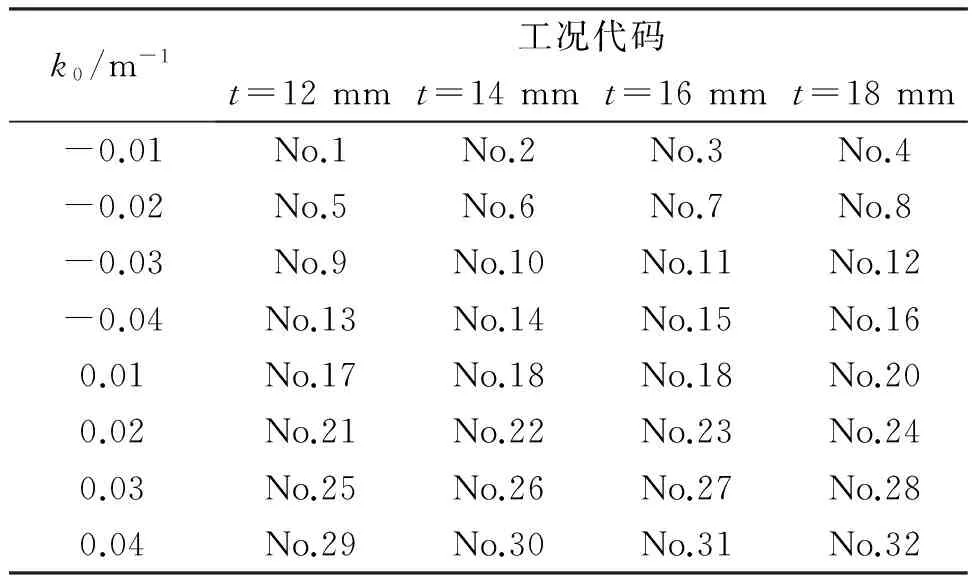
表2 计算工况
注:k0为初始弯曲曲率;t为壁厚。
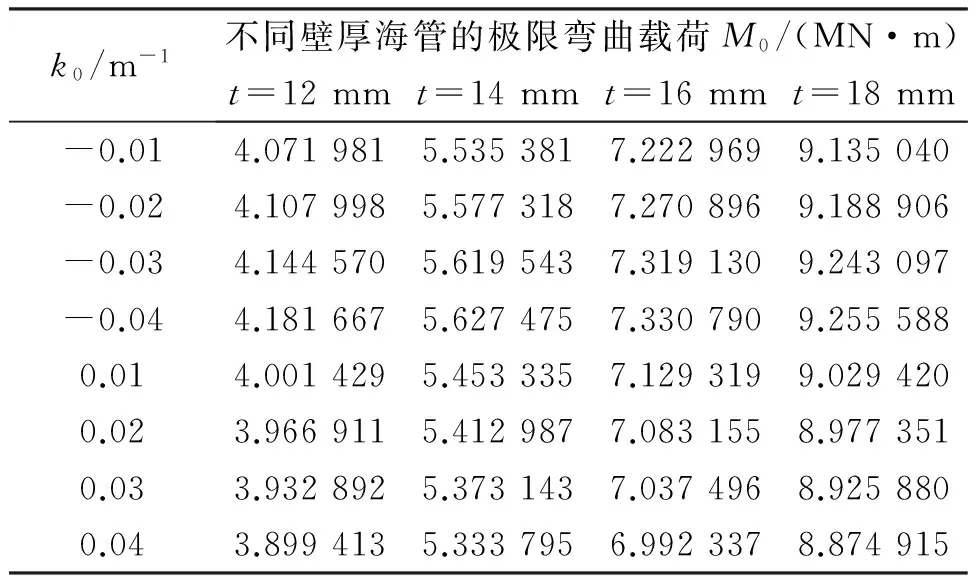
表3 无裂纹海管的极限弯曲载荷M0计算结果

图7 无裂纹海管的极限弯曲载荷
从图7中可以看出,无裂纹海管的极限弯曲载荷随着壁厚的增大而增大,且增长趋势较快。随初始弯曲曲率的增大而减小,但变化趋势不是很明显。由此可见,增加管壁厚有利于提高无裂纹海管的抗弯能力。
3.1 壁厚
对于具有相同壁厚的海管,其极限弯曲载荷由于受到裂纹的影响将会大幅减小。本文对初始弯曲曲率为-0.01 m-1的海管进行了研究。壁厚t=12、14、16、18 mm,裂纹半角分别为θ=π/16、π/8、3π/16、π/4、5π/16、3π/8、7π/16、π/2,根据式(18)进行计算,计算结果如表4所示。将表4中数据绘图,如图8所示。

表4 k0=-0.01 m-1时含裂纹海管的ML随壁厚变化计算结果
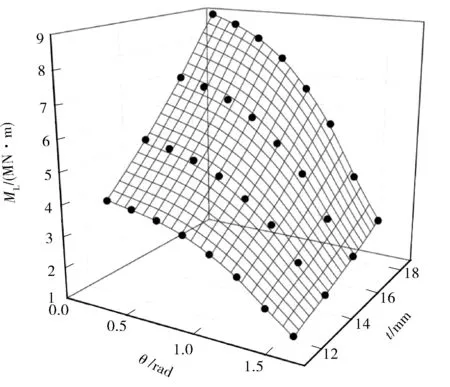
图8 k0=-0.01 m-1时的有裂纹海管的极限弯曲载荷与壁厚、裂纹半角的关系
从图8中可以看出,极限弯曲载荷随裂纹半角的增大而减小,随壁厚的增大而增大。在裂纹为零处,极限弯曲载荷变化趋势与无裂纹海管的极限弯曲载荷变化趋势一致。壁厚较大的海管,极限弯曲载荷也较大,但其随裂纹半角的增大,极限弯曲载荷变小的趋势更快一些。对于裂纹半角较大的海管,其极限弯曲载荷随壁厚的增大而增大,但增长趋势比较缓慢。
3.2 初始弯曲曲率
初始弯曲曲率不仅影响无裂纹海管的极限弯曲载荷,也对有裂纹海管的极限弯曲载荷产生一定的影响,在壁厚t=12 mm时,研究初始弯曲曲率和裂纹半角的大小对极限弯曲载荷的影响,初始弯曲曲率的取值为-0.01,-0.02,-0.03,-0.04,0.01,0.02,0.03,0.04,裂纹半角分别为θ=π/16、π/8、3π/16、π/4、5π/16、3π/8、7π/16、π/2,根据(18)式进行计算,计算结果如表5所示,图9为其相应的三维图。

表5 t=12 mm时含裂纹海管的ML随初始弯曲曲率变化的计算结果
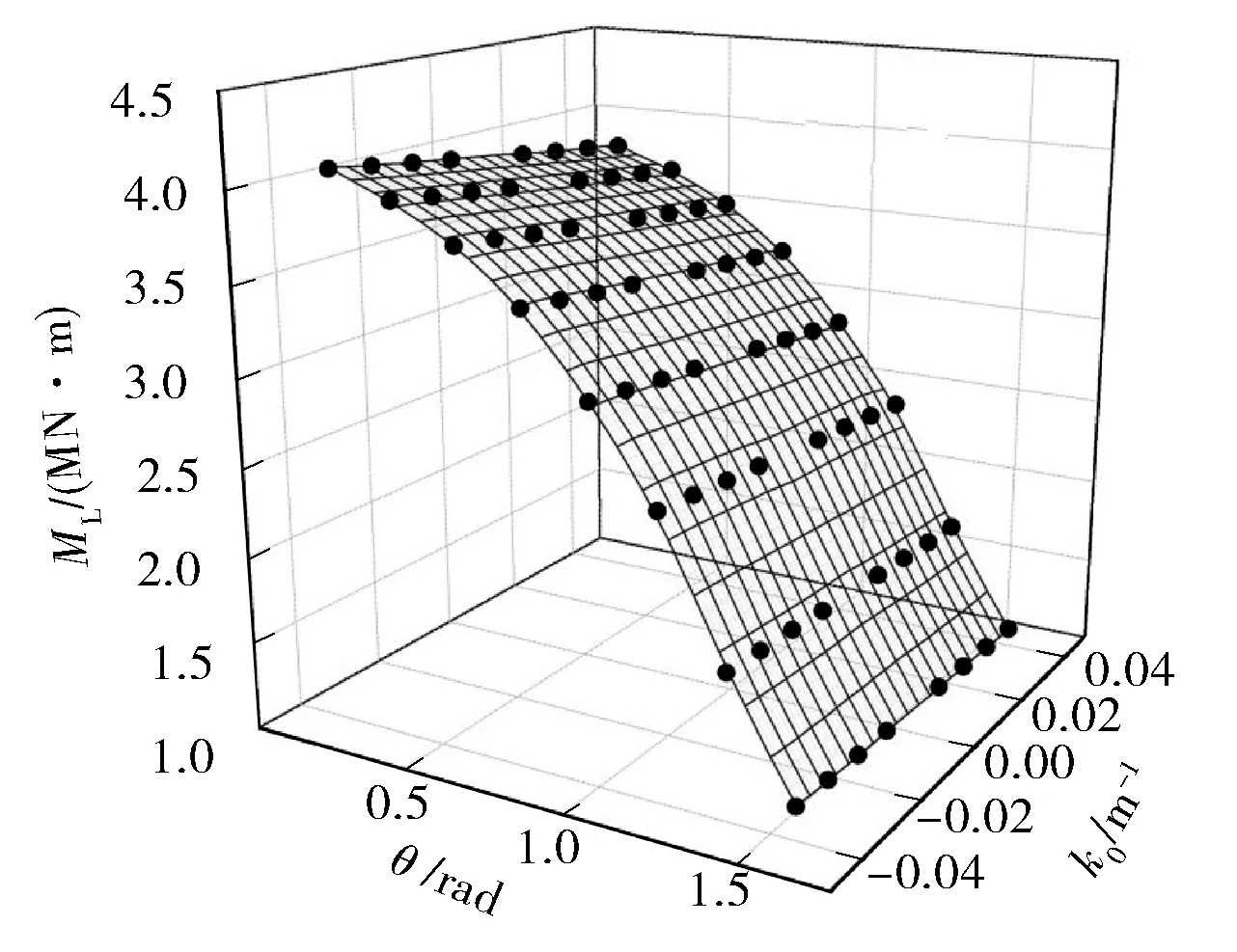
图9 t=12mm时,海管极限弯曲载荷与裂纹半角、初始弯曲曲率的对应关系
从图9中可看出,对于有同一裂纹半角的海管,随着初始弯曲曲率的增大,其极限弯曲载荷减小。无论是正向的初始弯曲曲率,还是负向的初始弯曲曲率,都没有改变极限弯曲载荷随裂纹半角的增大而减小的曲线变化规律。在裂纹半角接近π/2时,极限弯曲载荷随初始弯曲曲率变化的范围较小,这主要是由于裂纹角越大,海管的局部越容易产生应力集中,其局部越容易失稳,使得海管的极限弯曲载荷越小。
4 结论
本文总结了有关无裂纹海管的极限弯曲载荷的理论计算方法,其中包括本文所提出的理论计算公式。在此基础上,分析了Miller和Zahoor有关含裂纹海管的极限弯曲载荷理论计算方法。用有限元方法进行了计算,得到了多组裂纹半角对应的极限弯曲载荷值,并用Origin软件进行了函数拟合,得到了有裂纹海管的极限弯曲载荷表达式。该表达式考虑了正向的初始弯曲曲率和负向的初始弯曲曲率以及在弯曲变形中海管截面的椭圆化变形。通过对该表达式中的壁厚、初始弯曲曲率、裂纹半角的研究得到的结论如下:
1) 极限弯曲载荷随裂纹半角的增大而减小,随壁厚的增大而增大,在裂纹为零处,极限弯曲载荷变化趋势与无裂纹海管的极限弯曲载荷变化趋势一致。壁厚较大的海管,极限弯曲载荷也较大,但其随裂纹半角的增大,极限弯曲载荷变小的趋势更快一些。对于裂纹半角较大的海管,其极限弯曲载荷随壁厚的增大而增大,但增大趋势趋于缓慢,故较大的壁厚有利于提高海管的极限弯曲载荷。
2) 对于有同一裂纹半角的海管,随着初始弯曲曲率的增大,其极限弯曲载荷减小。无论是正向的初始弯曲曲率还是负向的初始弯曲曲率,都没有改变极限弯曲载荷随裂纹半角的增大而减小的曲线变化规律。在裂纹半角接近π/2时,极限弯曲载荷随初始弯曲曲率变化的范围较小,这主要是由于裂纹角越大,海管的局部越容易产生应力集中,其局部越容易失稳,使得海管的极限弯曲载荷越小。
3) 海管在进行焊接时,将会有残余应力、焊缝或者各种结构形式的裂纹等缺陷的存在。在对海管进行多次加载-卸载的过程中,其缺陷使得海管材料力学性能发生了大的改变,远比完整海管的力学性能复杂的多,且这些缺陷在循环弯曲载荷作用下会对海管的疲劳寿命产生很大的影响。建议用理论、试验、数值模拟等多种方法结合来进行研究。
4) 在进行卷管铺设时,海管的材料有多种,其结构也较为复杂,例如,双层管,夹心管,涂有外涂层的海管等,像这种结构和材料都较为复杂的海管,在受到多种复杂的外载荷作用时,其变形也更为复杂,未来的研究方向可以考虑复杂结构的海管在卷管铺设中的弹塑性变形。
:
[1] Miller A G. Review of limit loads of structures containing defects[J]. International Jouranla of Pressure Vessels Piping, 1988,32: 197-327.
[2] Zahoor A. Ductile fracture handbook[M]. California USA: Electric Power Research Institute, 1991: 11-34.
[3] Chattopadhyay J, Dutta B K, Kushwaha H S. Experimental and analytical study of three point bend specimen and throughwall circumferentially cracked straight pipe[J]. International Journal of Pressure Vessels and Piping, 2000, 77:455-471.
[4] Chattopadhyay J ,Pavankumar T V, Dutta B K, et al. Fracture experiments on through wall cracked elbows under in-plane bending moment: Test results and theoretical/numerical analyses[J]. Engineering Fracture Mechanics, 2005, 72:1461-1497.
[5] Chattopadhyay J, Kushwaha H S, Roos E. Some recent developments on integrity assessment of pipes and elbows. Part I: Theoretical investigations[J]. International Journal of Solids and Structures, 2006, 43:2904-2931.
[6] Chattopadhyay J, Tomar A K S, Dutta B K, et al. Elastic-plastic J and COD estimation schemes for throughwall circumferentially cracked elbow under in-plane closing moment[J]. Engineering Fracture Mechanics, 2005, 72:2186-2217.
[7] Chattopadhyay J, Venkatramana W, Dutta B K, et al. Plastic collapse moment equations of throughwall axially cracked elbows subjected to in-plane bending moment[J]. Engineering Fracture Mechanics, 2008, 75:2260-2275.
[8] Chattopadhyay J, Tomar A K S. New plastic collapse moment equations of defect-free and throughwall circumferentially cracked elbows subjected to combined internal pressure and in-plane bending moment[J]. Engineering Fracture Mechanics, 2006, 73:829-854.
[9] Yahiaoui K, Moreton D N, Moffat D G. Evaluation of limit load data for cracked pipe bends under opening bending and comparisons with existing solutions[J]. International Journal of Pressure Vessels and Piping, 2002, 79:27-36.
[10] Lei Y. A review of limit load solutions for cylinders with axial cracks and development of new solutions[J]. International Journal of Pressure Vessels and Piping, 2008, 85:825-850.
[11] 帅健.含裂纹管道的失效评定曲线的实例验证[J].机械强度,2003,25(3):251-253.
[12] 韩克江,帅健,王俊强,等.管道大范围屈服断裂评估的研究现状与进展[J].力学进展,2012,42(1):29-40.
[13] 周晶,冯新,李昕.海底管线全寿命安全运行的关键问题研究[J].工程力学,2011(增刊Ⅱ):97-108.
[14] 金伟良,付 勇,赵冬岩,等.具有裂纹损伤的海底管道断裂及疲劳评估[J].海洋工程,2005,23(13):7-16.
[15] Netto T A,Botto A. Fatigue Life Assessment of Reeled Risers[C]// Offshore Conference Technology, 2007, 1-7.
[16] Netto T A, Botto A, Lourenco M I. Fatigue performance of pre-strained pipes with girth weld defects: local deformation mechanisms under bending[J]. International journal of fatigue, 2008, 30: 1080-1091.
[17] Tkaczyk T, Dowd N P O, Nikbin K, et al. Fracture Assessment of Elastic-Plastic Steel Pipelines Subject to Multi-cycle Bending[C]//Proceedings of the Nineteenth (2009) International Offshore and Polar Engineering Conference, 2009,110-117.
[18] Tkaczyk T, Dowd N P O,Nikbin K, et al. A Non-Linear Fracture Assessment Procedure for Pipeline Materials with a Yield Plateau[C]//Proceedings of the Nineteenth (2009) International Offshore and Polar Engineering Conference, 2009, 100-109.
[19] Spence J, Findlay G E. Limit load for pipe bends under in-plane bending[C]// Proceeding of 2nd international conference on pressure vessel technology, 1973, 393-403.
[20] Calladine C R. Limit analysis of curved tubes[J].Journal of Mechanical Engineering Science, 1974, 16(2): 85-7.
[21] Goodall I W. Large deformations in plastically deforming curved tubes subjected to in-plane bending[R]. UK: CEGB RD/B/N4312, 1978.
[22] Touboul F, Ben D M, Acker D. Design criteria for piping components against plastic collapse: application to pipe bend experiments[C]//Proceeding of 6th international conference on pressure vessel technology, 1988, 73-84.
[23] 张九菊,段梦兰,马建敏,等.基于深海卷管铺设的海管椭圆度分析[J].应用数学和力学,2013,34(6):552-563.

