立方体测混凝土抗压强度时的破裂形态与机制
康亚明,贾 延,罗玉财
(1:北方民族大学 化学与化学工程学院,宁夏 银川 750021; 2: 北方民族大学 数学与信息科学学院,宁夏 银川 750021)
抗压强度是混凝土的最基本性能指标,我国规范中常用轴心和立方体这两个抗压强度指标是用不同形状试件测得的,在数值上立方体抗压强度略大于轴心抗压强度,规范也给出了详细的换算系数,该系数实际上是强度形状效应的校正[1-2].
形状效应是岩石或混凝土等脆性材料强度测试中的一个基本问题,已有的研究成果多集中在模型试验和数值模拟,得出的结论多为定性的描述.文献[3]对不同形状的混凝土试件单轴压缩强度进行了系统的试验研究,结果高宽比大于某一值时可基本消除端面约束的影响,也即形状效应随高宽比的增大而减弱.文献[4-6]认为形状效应与试验机压头和试件受压面之间的摩擦力有直接关系.文献[7-13]基于有限元分析了混凝土强度的形状效应.文献[14-15]对岩石的形状效应进行了三维数值模拟,显示强度随高宽比的增大而减小,高宽比大于2.5时趋于稳定.以上研究代表了目前岩石或混凝土强度形状效应研究的基本现状,欠缺对强度形状效应及其来源的理论分析,缺乏基于理论分析基础上的定量结论,这也是目前形状效应没有出现定量研究成果的根本原因.
鉴于此,笔者对立方体测抗压强度时的剪切带进行了分析,并基于强度参数反算了不同强度等级混凝土真实的破裂角范围和最危险破裂角,通过数据定量反映了高宽比与强度之间的关系,以揭示高宽比大于某一值之后可消除形状效应的内在机理,也为今后建立强度形状效应理论解的打下基础.
1 单轴压缩时立方体的破坏特征与机理
1.1 单轴应力状态下的力学模型
立方体测抗压强度时试块处于单轴应力状态,其力学模型如图1所示.

图1 轴向压缩时的应力分量Fig.1 Stress component of axial compression
根据一点的应力状态,斜截面m-m上法向正应力σn和切向剪应力τn分别为
(1)
(2)
在图1中,σ1可分解为与斜截面平行的剪力τn和与斜截面内法线方向一致的正应力τn,τn是引起剪切破坏的“下滑力”,而σn提高了破裂面上滑动摩擦阻力.显然,斜截面角度β的变化引起了τn和σn的增减,其中45°斜截面上剪力最大,但45°斜截面上的抗剪强度并不一定是最小的,所以最终的破坏并不是在剪力最大或抗剪强度最小的截面,而是在剪应力和抗剪强度差值最大的截面上.
1.2 莫尔-库仑准则下强度特征
根据莫尔-库仑准则,β斜截面的抗剪强度τf可表示为
τf=c+μσn
(3)
式中:c为粘聚力,MPa;σn同前,由式(1)确定,MPa;μ为斜截面上的摩擦系数,与剪切面本身结构性状有关,这里取μ=tgφ,φ为混凝土的内摩擦角,°.
当轴向压力达到一定值后,试块体内产生压应力和剪应力,剪力和抗剪强度差值最大的某一斜截面将率先发生破坏.最危险破裂面从极限平衡状态到失稳时,其剪应力τn与抗剪强度τf之间应当满足下列失稳条件[16]:
τn≥τf=c+μσn
(4)
将式(1)、(2)代入式(4)中,得:

(5)
1.3 摩尔-库仑准则的单位化
为了从几何图形上直观观察剪切破坏发生的范围,这里将莫尔-库仑准则单位化,也即将式(5)左右两边同除以σ1/2,得
sin2β≥2μcos2β+2c/σ1
(6)
在式(6)中,记ξ=c/σ1,定义为剪压强度比,这样式(6)可以简化为
sin2β≥2μcos2β+2ξ
(7)
1.4 摩尔-库仑准则的图解法
从式(6)或式(7)可以看出,只要给出混凝土的强度参数c、μ和σ1,就可以反算出破裂角范围和最危险破裂角.为此,对(7)进行移项:
sin2β-2μcos2β-2ξ≥0
(8)
显然,式(8)大于零的范围为剪力大于抗剪强度的范围,记f(β)=sin2β-2μcos2β-2ξ,将f(β)的函数图绘制出来,将更加直观的看出破裂角的分布范围(图2).
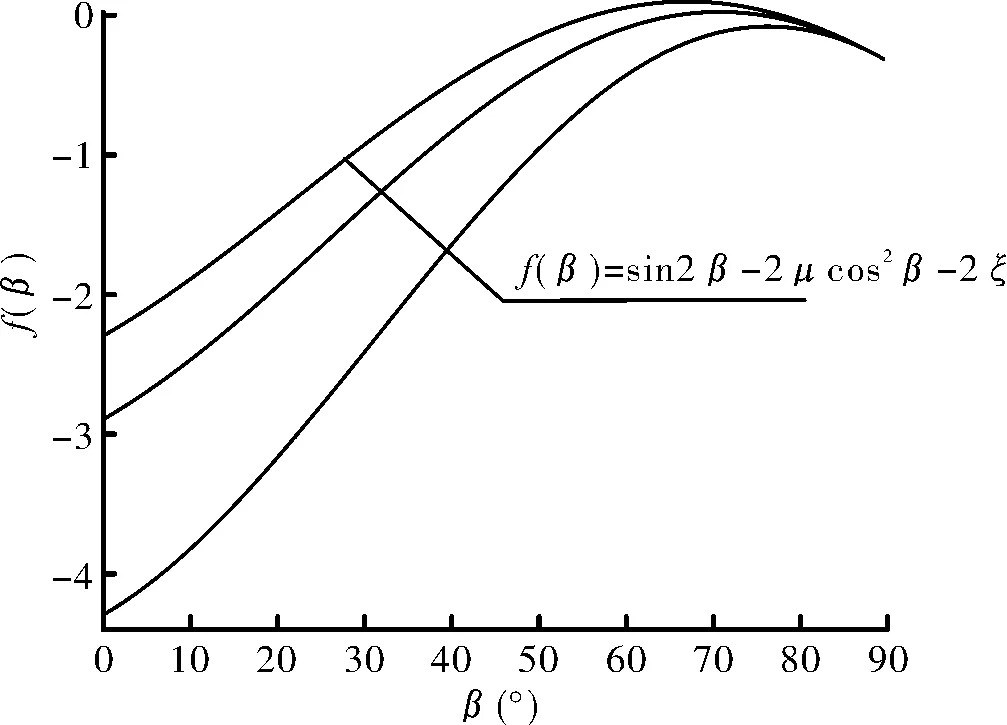
图2 摩尔-库仑准则的图解法Fig.2 Graphic method of the Mohr-Coulomb criterion
在图2中,通过f(β)与横坐标的位置关系可以判断能否发生剪切破坏,以及发生剪切破坏时剪切面的位置,可能的位置关系有三种情况:
(1)相离(f(β)<0,也即τn<τf)
此时抗剪强度始终大于剪力,不会发生剪切破坏.
(2)相交于一点(f(β)=0,也即τn=τf)
此时抗剪强度有且只有一个位置等于剪力,此位置对应的横坐标记为β,β位置最有可能发生剪切破坏.
(3)相交于两点(f(β)>0,也即τn>τf)
若f(β)与横坐标相交于两点,此区间的范围记为[βmin,βmax],在这个区间内,剪应力和抗剪强度差值最大的位置为最危险斜截面.
需要指出的是,剪应力大于抗剪强度是剪切破坏的必要条件,充分条件是剪应力与抗剪强度差值最大,那么βmin就是可能发生剪切破坏时的最小破裂面角度,而βmax是上限,
2 普通混凝土的破裂角范围与最危险破裂角
2.1 混凝土的强度参数与相关系数
对于不同强度等级的混凝土,《混凝土结构设计规范》中给出了其抗剪和抗压强度标准值,据此算出自定义的剪压强度比ξ=τ/σ1,如表1所示.

表1 规范中不同强度等级混凝土的强度参数标准值[17]
若要基于式(7)计算最危险破裂角,还需要给出与剪切性能相关的粘聚力和摩擦系数,但是在工民建行业,混凝土结构设计以弹性为主,基本不考虑其塑性特征,所以在《混凝土结构设计规范》中并未给出不同等级混凝土的粘聚力c和内摩擦角φ,丛宇[18]通过实验得到了不同等级混凝土的剪切参数,如表2所示.可以看出,内摩擦角随强度等级在3°范围内窄幅波动,反映在摩擦系数上,大致在1.4~1.6之间波动.为了统一,对于不同等级混凝土的强度参数均取标准值,对应的摩擦系数μ如表3所示.

表2 不同强度等级混凝土抗剪强度标准值[18]

表3 取标准值时不同强度等级混凝土破裂面摩擦系数
2.2 破裂角范围与最危险破裂角的反算
将表3中的数据代入式(8)中,将其曲线绘制在图3所示的坐标系中,图3中右下角为横坐标以上部分的放大图.此部分是剪应力大于抗剪强度时的区域,与横坐标的交点为发生剪切破坏时破裂角的上下限,每条曲线的峰值表示剪应力与抗剪强度差值最大,对应的角度为最可能或最危险破裂角,为了对比差异,将不同强度混凝土剪切破坏时的破裂角范围和最危险破裂角汇总起来如表4所示.

表4 不同强度等级混凝土的破坏角范围和最危险破裂角/(°)
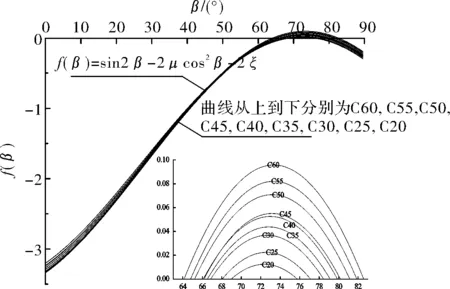
图3 不同强度等级混凝土破裂角范围的图解法Fig.3 Graphic method for fracture angle range of concrete with different strength grades
3 立方体测抗压强度与破裂形态
3.1 单轴压缩时的破裂形态
国标之所以把立方体抗压强度值作为评定混凝土强度的基本指标,并以规范的形式确定了立方体抗压强度的法律地位,主要是考虑到了立方体抗压强度在实验测试时的稳定性.立方体测抗压强度时,典型的破裂形态如图4所示,立方体端头处于应力集中影响范围内,随着应力的增大,轴向变形同步增大,试块的外表面的开始崩裂,最后上下形成一对 “核”,破坏面是上下近似对称的一对圆锥体外表面面积.

图4 立方体测抗压强度时的破裂形态Fig.4 The fracture morphology of cube in the measurement of compressive strength
3.2 端面强约束时的剪切带特征
如图5所示,当试块端面与试验机压头之间为理想强约束时,边界条件约束了试块端面水平方向的位移,这样就限制了部分破裂面.在立方体中破裂面方位角被约束限制在了45°及其以下,而45°以下这些区域中的斜截面上,对角线附近的45°斜截面最有可能发生剪切破坏,破坏形态为图5所示的四种对称模式.

图5 上下端面强约束条件下的剪切滑动面Fig.5 Shear slip surface of cube subjected to strong constraint from upper and lower surfaces
在图5中,(a)和(b)是试件上部发生剪切破坏时左右对称情况,(a)中的阴影部分有向左下滑动的趋势,而(b)中的阴影部分有向右下滑动的趋势;同理,(c)和(d)是试件下部发生剪切破坏时左右对称情况,(c)中的阴影部分有向左上滑动的趋势,而(d)中的阴影部分有向右上滑动的趋势.当立方体为理想均质各向同性和完全弹性材料时,立方体的上下受压面完全平行时,左右两部分向左和向右滑动趋势是互相抵消的,叠加过程和效果如图6所示.

图6 上下端面强约束条件下剪切带的叠加Fig.6 The superposition of shear bands of cube subjected to strong constraint for upper and lower surfaces
图6中(a)是上部左右剪切带的叠加,(b)是下部左右剪切带的叠加,叠加后的I区保持原来的趋势,II区中两种方向相反滑动发生了抵消,为左右剪切带抵消平衡区.上部和下部是两种对称情况,最终立方体中总的剪切带是这两种模式的叠加,最终的剪切带如图7所示.

图7 上下端面强约束条件下的剪切带分布Fig.7 Shear band distribution of cube subjected to strong constraint from upper and lower surfaces
在图7中,立方体中存在左右对称的I区和上下对称的II区,I区其变形趋势是脱离立方体向外侧崩解的趋势,II区一方面是端头约束影响区,另外也是左右剪切带平衡区,表现为只有竖直方向的位移,这也是为什么立方体最后的破裂形态绝大多数是X形状的原因所在.
通过上面的受力分析可以看出,立方体中并没有出现均匀的轴向压缩,因此立方体抗压强度并不是混凝土被“压碎”所对应的强度,而是包括压缩和剪切两部分,且以压缩为主、剪切为辅的压剪破坏.我国国际标准将立方体抗压强度以规范的形式确定下来,并赋予其法律地位,这样其测试结果就具有可比性,也是评定混凝土强度等级和施工质量验收的依据,可以唯一地去指导工业生产,具有重要的技术指导意义.
4 分析与讨论
4.1 立方体强度偏大的内在机理
从表4中可以看出,普通混凝土的最危险破裂角大致在72.5~73.5°附近,而立方体试块中45°以上斜截面被边界约束所限制,而45°以下斜截面上的抗剪强度又大于剪应力,导致实际破裂面与最危险破裂面不一致,最危险的情况没有发生,最终的破坏是以压缩为主而不是以剪切为主,而混凝土的抗压强度远大于抗剪强度,故用立方体测得的强度就比实际强度偏大,这也就是混凝土强度规范中立方体抗压强度和棱柱体抗压强度需要修正的原因所在,也是形状效应产生的理论机理.基于这一思路,结合边界条件对破裂路径的影响,将不同斜截面上的强度进行比较,就可以建立强度形状效应的解析式.
4.2 消除形状效应的临界高宽比
如前所述,立方体中最危险破裂面在边界约束影响范围内,最终破坏没有发生在最危险处,那么是否可以通过提高试件的高宽比让最危险破裂面处于边界约束影响之外,这个高宽比即为消除形状效应的临界高宽比.为了对比不同高宽比下最危险破裂面差异,这里取几种典型情况,如图8所示.

图8 不同高宽比时的最危险破裂角对比Fig.8 Comparison of the most dangerous fracture angles at different aspect ratios
在图8中,对于不同高径比的混凝土试块,由于上下端面水平位移被约束,导致轴向受压时破裂路径发生了改变,而对角线附近的破裂面成为方位角最大的破裂面,但不同高宽比时对角线倾角不一样,如当高宽比为4时,对角线方位角在76°附近,而常见混凝土的最危险破裂角都小于此角度,故最危险情况可以发生;高宽比等于3时,对角线方位角与莫尔-库仑准则反算出的混凝土真实破裂面方位角大致相当,故3倍高宽比是真实值与实测值趋于一致的临界值;而当高宽比小于3时,对角线方位角均小于真实破裂面方位角.显然,当实际破坏时的破裂面方位角小于真实的破裂面方位角时,破坏并没有发生在最危险处,测得的强度就比实际强度大.通过上述的对比可以看出,三倍高宽比时,实际破裂面与真实破裂面方位角较为接近,三倍高宽比及其以上基本上可以消除端面约束对强度的影响,故三倍高宽比是消除形状效应的临界值.
如图9所示,对于普通混凝土而言,三倍高宽比的本质是保证了纯压区高度h,对于这一问题,过镇海等人根据大量实验以及数值模拟结果,给出了一个普遍性的结论:一般认为,高宽比在2~3时,可基本消除端面约束的影响.通过数据的反算,定量证明了这一经验性结论较为准确的内在力学机理,也进一步明确了消除端面约束的临界高宽比接近于3,考虑到实际端头约束并非完全约束,临界高宽比略小于3.

图9 试件中的纯压区[2]Fig.9 Pure pressure region in prism test specimen
4.3 立方体抗压强度与轴心抗压强度的折减
边界条件对强度影响的本质是应力集中改变了破裂路径,而不同的破裂路径对应着不同的强度,强约束边界条件下棱柱体和立方体中的实际破裂路径不同,其结果是测得的抗压强度不一致,两者之间需要折减换算才能统一.用棱柱体测得的轴心抗压强度与立方体抗压强度的比值规范有明确规定,在新版规范中又做了进一步调整,如式(9)所示[17]:
(9)
式中:fck为棱柱体试件测得的具有95%保证率的0.88混凝土轴心抗压强度标准值,MPa;系数0.88是考虑实际结构中的混凝土与试块混凝土强度之间的差异等因素而确定的修正系数;α1为轴心抗压强度与立方体抗压强度的比值(见表5);α2为混凝土脆性系数;fcu,k为用立方体测得的具有95%保证率的混凝土抗压强度,MPa.

表5 强度折减系数α1的取值[17]
旧规范中对于轴心抗压强度fck和立方体抗压强度fcu,k修正系数α1统一取0.76,而新规范中C50以上系数略有提高.对立方体强度进行折减,就是考虑到了立方体抗压强度高于真实强度,本质上是对强度形状效应的修正.
5 结论
以规范中立方体测混凝土强度问题为背景,揭示了边界条件是通过改变破裂路径最终影响了强度,而不同的破裂路径对应着不同的强度,通过建立不同破裂面上的强度公式,结合边界条件可以建立形状效应的解析解,这也是规范中混凝土强度形状效应的内在机理,主要结论有:
(1)立方体中存在左右对称的崩解区和上下对称的刺入区,前者的变形趋势是脱离立方体向外侧崩解,后者一方面是端头约束影响区,另外也是左右剪切带平衡区,表现为只有竖直方向的位移;
(2)单轴压缩时混凝土的真实破裂角在64~83°之间,最危险破裂角在73°附近,而立方体中45°以上潜在破裂面被边界约束所限制,而45°以下斜截面上抗剪强度又大于剪应力,导致实际破裂面与最危险破裂面不一致,故用立方体测得的抗压强度偏大;
(3)反算出的最危险破裂角表明,三倍高宽比是消除端面约束影响的临界值,此时最危险破裂面基本脱离端头约束的影响,真实破裂面与实际破裂面趋于一致;
(4)普通混凝土发生剪切破坏时的破裂面方位角在64~83°之间,在立方体中不存在发生剪切所必须的试件高度,故立方体测得的抗压强度主要是抗压强度,压缩过程中产生的裂缝也是刺入区挤压产生的张拉裂缝;
(5)立方体测定的抗压强度本质上是介于纯压缩和纯剪切之间的以压缩为主的压剪强度,棱柱体测得的轴心抗压强度是以剪切为主的剪压强度,由于剪切和压缩比重的不同,立方体的强度理论上要大于棱柱体的强度.
[1] 戎明君,陆建雯,姚燕,等. 普通混凝土力学性能试验方法标准:GB/T 50081-2002 [S].北京:中国建筑工业出版社,2003:12-14.
RONG Mingjin, LU Jianwen, YAO Yan, et al.Standard test method for plain concrete mechanical properties: GB/ T50081-2002 [S]. Beijing: China Architecture & Building Press, 2003:12-14.
[2] 过镇海. 混凝土的强度和变形——试验基础和本构关系[M].北京:清华大学出版社,1997:41-43.
GUO Zhenhai. Strength and deformation of concrete test and constitution [M]. Beijing: Tsinghua University Press,1997:41-43.
[3] VAN MIER J G M. Strain-softening of concrete in uniaxial compression [J]. Materials and Structures,1997,30: 195-209.
[4] L′HER MITE R. Idées actuelles sur la technologie dubéton [J]. Bull RILEM,1954( 18) : 27-40.
[5] 康政,唐欣薇,秦川,等. 基于细观离散元的混凝土端部效应分析[J].哈尔滨工业大学学报,2013,45(12):94-98.
KANG Zheng, TANG Xinwei, QIN Chuan, et al. End effect of concrete by meso-scale discrete element modeling [J]. Journal of Harbin Institute of Technology,2013,45(12):94-98.
[6] HANSEN H,KIELLAND A,NIELSEN K E C,et al. Compressive strength of concrete-cube or cylinder[J]. Bull RILEM,1962( 17) : 31-33.
[7] INDELICATO F,PAGGI M. Specimen shape and the problem of contact in the assessment of concrete compressive strength[J]. Materials and Structures,2008,41: 431-441.
[8] 马怀发,陈厚群,黎保琨. 混凝土试件细观结构的数值模拟[J].水利学报,2004,35(10):27-35.
MA Huaifa, CHEN Houqun, LI Baokun. Meso-structure numerical simulation of concrete specimens [J]. Journal of Hydraulic Engineering,2004,35(10):27-35.
[9] 刘金庭,朱合华,莫海鸿. 非均质混凝土破坏过程的细观数值试验[J].岩石力学与工程学报,2005,24(22):4120-4133.
LIU Jinting, ZHU Hehua, MO Haihong. Mesostructure nmerical test of nonuniformity concrete damage process[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(22):4120-4133.
[10] 林皋,李建波,赵娟,等. 单轴拉压状态下混凝土破坏的细观数值演化分析[J].建筑科学与工程学报,2007,24(1):1-6.
LIN Gao, LI Jianbo, ZHAO Juan, et al. Mesoscopic numerical evolution analysis of concrete damage under uniaxial tension and compression[J]. Journal of Architecture and Civil Engineering,2007,24(1):1-6.
[11] 党发宁,韩文涛,郑娅娜,等.混凝土破裂过程的三维数值模型[J].计算力学学报,2007,24(6):829-833.
DANG Faning, HAN Wentao, ZHENG Yana, et al. 3D numerical simulation of failure process of concrete[J]. Chinese Journal of Computational Mechanics, 2007,24(6):829-833.
[12] 陈健云,刘智光. 混凝土试样单轴压缩端面效应及破坏数值模拟[J]. 大连理工大学学报,2013,53(1) : 90-96.
CHEN Jianyun, LIU Zhiguang. Numerical simulation for failure process and effect of boundary restraint of concrete specimens in uniaxial compression [J]. Journal of Dalian University of Technology, 2013, 53(1) : 90-96.
[13] 苏捷,方志. 普通混凝土与高强混凝土抗压强度的尺寸效应[J]. 建筑材料学报,2013,16(6:):1078-1086
SU Jie, FANG Zhi. Scale effect on cubic compressive strength of ordinary concrete and highstrength concrete [J]. Journal of Building Materials,2013,16(6:):1078-1086.
[14] 梁正召, 唐春安,张娟霞,等.岩石三维破坏数值模型及形状效应的拟研究[J]. 岩土力学, 2007, 28(4): 699-704.
LIANG Zhengzhao, TANG Chunan, ZHANG Juanxia, et al. Three-dimensional damage model for failure process of rocks and associated numerical simulation of geometry effect [J]. Rock and Soil Mechanics,2007,28(4):699-704.
[15] 麦戈,唐照平,唐欣薇.岩石单轴压缩端部效应的数值仿真分析[J].长江科学院院报,2013,30( 6) : 68 -71.
MAI Gem,TANG Zhaoping, TANG Xinwei. Numerical simulation of rock′s end constraint effect under uniaxial compression [J]. Journal of Yangtze River Scientific Research Institute, 2013,30( 6) : 68-71.
[16] 宋玉普. 多种混凝土材料的本构关系和破坏准则[M]. 北京:中国水利水电出版社,2002:71-72.
SONG Yupu. The constitutive model equations and failure criteria of multiform concrete materials [M]. Beijing: China Water Recourses and Hydropower Press,2002:71-72.
[17] 中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局. 混凝土结构设计规范: GB 50010-2010[S]. 北京:中国建筑工业出版社,2011
Ministry of Housing and Urban -Rural Development of the People′s Republic of China , General Administration of Quality Supervision, Inspection and Quarantine of the People′s Republic of China. Code for design of concrete structures: GB 50010-2010 [S]. Beijing: China Building Industry Press, 2011.
[18] 丛宇. 卸荷条件下岩石破坏宏细观机理与地下工程设计计算方法研究[D]. 青岛:青岛科技大学,2014
CONG Yu. Study on rock macroscopic and mesoscopic failure mechanism under unloading conditions and designing and calculating methods of underground engineering [D]. Qingdao: Qingdao Technological University, 2014.

