钢筋混凝土剪力墙结构多塑性铰区合理布置研究

梁兴文，王照耀，于 婧，吴继伟

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2.台州职业技术学院 建筑工程学院，浙江 台州 318000)

近年来，随着我国国民经济的快速发展，高层建筑的功能和结构类型日趋多样化.在高层建筑的结构体系中，剪力墙结构体系是常用体系之一.在水平地震作用下，通常剪力墙的底部截面弯矩和剪力最大，我国现行设计规范[1-2]、规程[3]将剪力墙结构底部设置为潜在的塑性铰区(底部加强部位).通过加强剪力墙结构底部的抗震措施保证底部加强区出现塑性铰后有足够的延性，以控制结构的变形和能量耗散，减小结构的地震内力[4-5].但是塑性铰区的塑性转动必须在可接受的范围之内.

设计高层剪力墙结构时，我国规范推荐使用振型分解反应谱法来确定结构的内力和位移，这种方法假定结构以第一振型为主.而最新研究[6-10]表明：在高烈度区，按照传统的反应谱法设计的只在底部设置塑性铰区的剪力墙结构会受到高阶振型的影响，从而大幅度地增加其地震反应.为了保证剪力墙结构在罕遇地震下安全可靠，使结构上部依然保持弹性，需要增加整个结构的截面配筋率，但这可能会带来结点处钢筋过密和经济性差的问题.随着结构高度不断增加，保证其上部处于弹性状态变得十分困难.

Panagiotou[11]等通过对结构进行数值分析，提出剪力墙结构双塑性铰区设计概念，即在结构底部和H/2高度处分别设置塑性铰区，可以有效减小高阶振型的影响.因此，确定高层剪力墙结构中塑性铰区的数量和布置位置尤为重要，合理地布置塑性铰区不仅能减小结构在罕遇地震作用下的内力，还可以降低经济成本.

基于Panagiotou[11]等研究者的思路，本文应用PERFORM-3D软件，分别建立了20层和40层的钢筋混凝土框架-核心筒结构非线性纤维模型，通过对比罕遇地震作用下塑性铰区数量和布置位置对结构体系地震反应的影响，提出高层建筑结构中剪力墙结构多塑性铰区的合理布置形式.

1 分析模型和分析方法

1.1 地震波的选取

为了研究剪力墙结构多塑性铰区对结构因高阶振型而产生附加效应的影响，本文采用非线性时程分析法进行研究.选取的地震波加速度反应谱和加速度时程曲线如图1和图3所示.已有研究[11]表明：当地震波的卓越周期处在0和结构第二自振周期之间时，对结构高阶振型会产生较大的影响(高阶振型效应)，使结构在地震中的内力显著增大.本文从太平洋地震工程研究中心(PEER)NGA数据库中选取RIN228和BOL090地震波，其中RIN228地震波记录取自1994年里氏6.6级Northridge地震，输入峰值加速度为0.87 g；另一条BOL090地震波记录取自1999年里氏7.1级Duzce地震，输入峰值加速度为0.82 g.其峰值谱加速度对应的周期均在0和0.85 s(小于模型第二自振周期)之间，故符合选取要求.

图1 加速度反应谱Fig.1 Acceleration response spectra

1.2 模型的建立

PERFORM-3D作为一款三维结构非线性分析和性能评估软件，具有稳定高效的结构非线性分析能力，在抗震弹塑性分析中大量应用，其对剪力墙利用纤维模型进行模拟，是一种基于材料的分析模型，提高了弹塑性分析的准确性[12].因此，本文在PERFORM-3D软件中建立钢筋混凝土框架-核心筒结构模型，并假定钢筋混凝土核心筒承担所有的水平荷载，外围的柱子和核心筒共同承担竖向荷载.模型在底部固结，并采用刚性楼板假设及楼层集中质量.框架-核心筒结构模型标准层平面图和模型的详细参数见图2和表1.

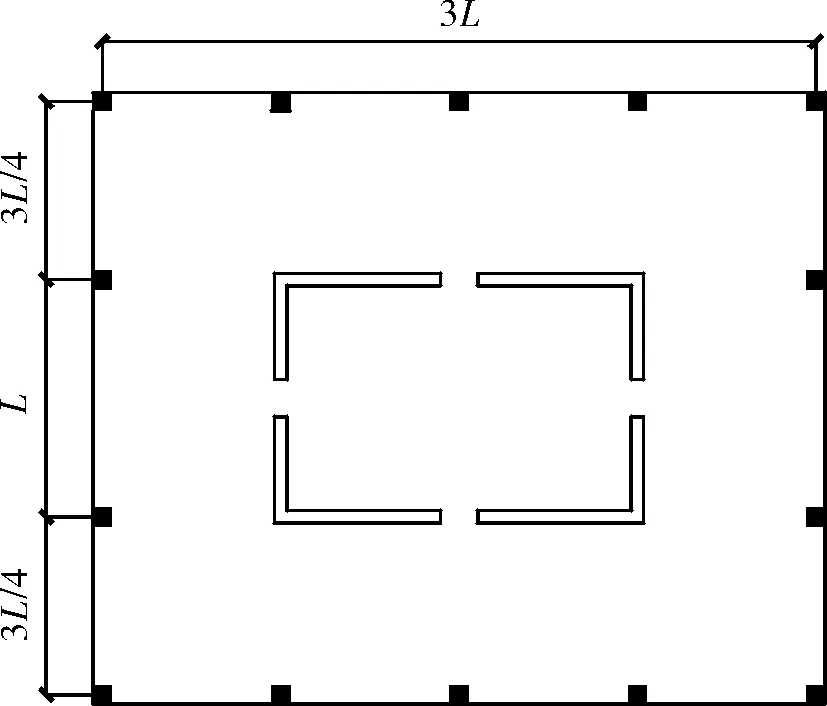
图2 模型平面图Fig.2 Typical plan of the models

基本参数20层40层层高h/m3.63.6结构总高度H/m72144第一自振周期/s2.565.14第二自振周期/s0.871.58第三自振周期/s0.290.55总重量G/kN138600811710核心筒宽度L/m9.615核心筒厚度t/m0.30.81核心筒面积A/m212.655.89

1.3 纤维截面模型

纤维截面模型可以准确地计算剪力墙中的弹塑性弯曲反应，因此在剪力墙结构的抗震性能研究中广泛应用[13-14].本文假定只允许剪力墙塑性铰区进入弹塑性阶段，其他部位都保持弹性状态.从而使用弹性截面剪力墙单元模拟弹性段，非弹性纤维截面剪力墙单元模拟塑性铰区.纤维截面定义时采用约束与非约束混凝土来模拟端部约束区和中间非约束区.

1.4 多塑性铰区布置

我国《高层建筑混凝土结构技术规程》[3]规定：剪力墙加强部位的高度可取底部两层和墙体总高度1/10二者的较大值，故本文塑性铰区高度均为H/10.多塑性铰区可以满足高层、超高层剪力墙结构进入弹塑性状态时上部曲率延性等的要求，增强结构塑性变形能力，确保结构不会发生严重破坏或倒塌，与单塑性铰区结构相比还可大量减少配筋.为讨论多塑性铰区合理布置，本文提出如图4所示的6种塑性铰区布置形式.其中形式A(SPH)为我国现行规范推荐形式，即在结构底部设置一个塑性铰；形式B(DPH)包含两个塑性铰区：一个在结构底部，另一个设置在H/2高度处；形式C(TPH-1)、D(TPH-2)、E(TPH-3)均包含三个塑性铰区，形式C中三个塑性铰区沿高度等距离分布，相邻塑性铰区之间距离H/3；形式D和E除在底部和H/2高度处设置塑性铰区外，分别在H/4和3H/4高度处设置塑性铰区；形式F(QPH)包含四个沿高度方向均匀分布的塑性铰区，相邻塑性铰区之间相距H/4.塑性铰区配筋率如表2所示(沿高度方向塑性铰区依次编号为1、2、3、4).

图3 地震动加速度时程曲线Fig.3 Seismic accelerogram

图4 塑性铰区布置形式Fig.4 Arrangement forms of plastic hinge region

多塑性铰区模型RIN228BOL0901234123440层SPH0.850.78DPH0.741.030.690.98TPH-10.660.860.840.630.790.72TPH-20.670.851.010.650.830.96TPH-30.691.020.830.640.970.78QPH0.630.791.000.810.600.750.930.7420层SPH1.411.28DPH1.251.381.111.17TPH-11.181.260.931.021.231.03TPH-21.171.151.331.031.11.18TPH-31.21.310.811.051.250.95QPH1.131.061.170.791.020.981.080.73

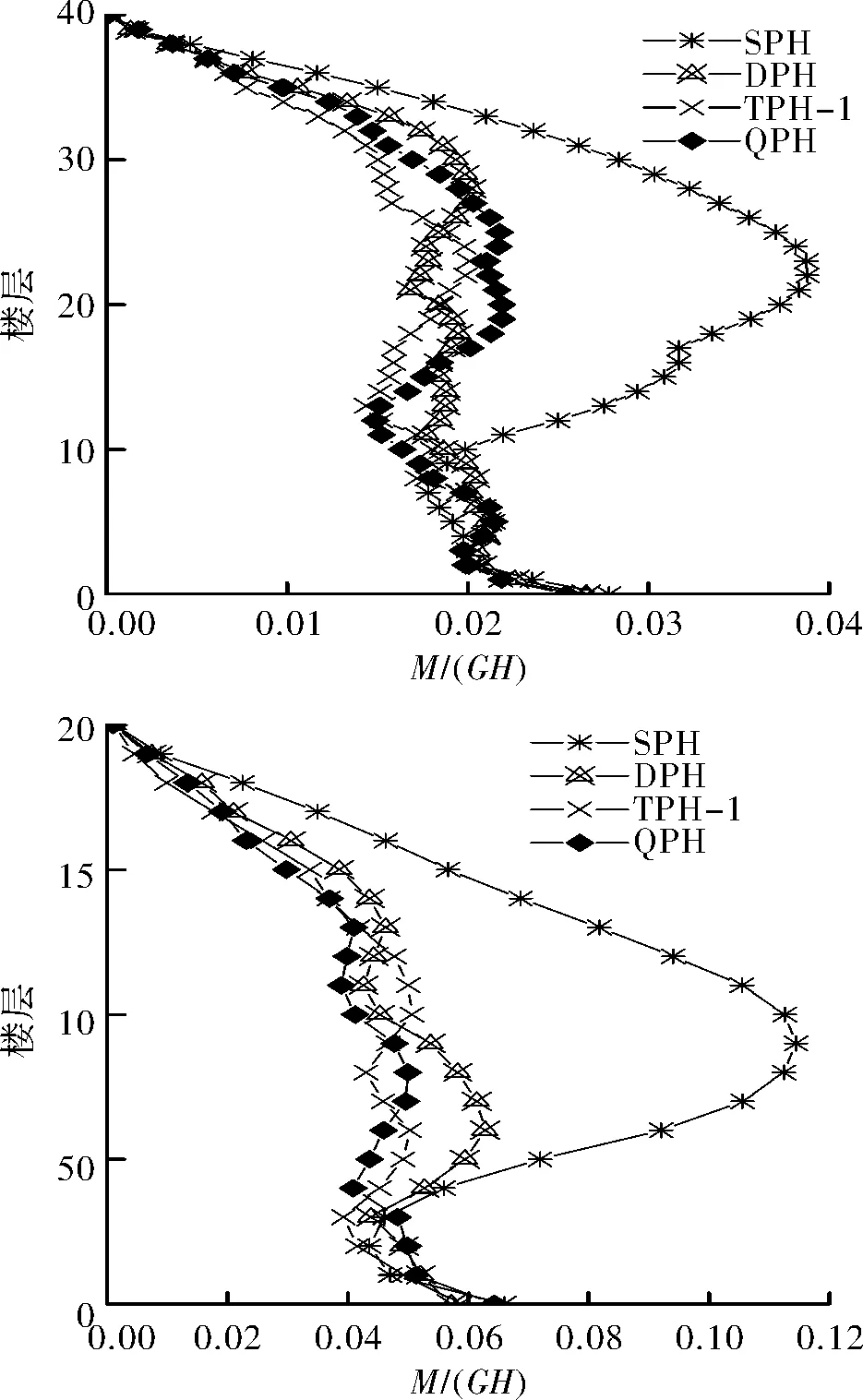
图5 BOL090作用下单塑性铰区与多塑性铰区模型弯距包络图Fig.5 Bending moment envelopes of single plastic hinge region and multi-plastic hinge region models for the record BOL090

2 结果分析

通过非线性时程分析法得到20层和40层模型分别在BOL090和RIN228地震波作用下的弯矩和剪力包络图，包络图中纵轴表示楼层数，横轴经过无量纲化的处理.其中弯矩包络图中，横轴为弯矩与模型重量和高度乘积的比值(M/(GH))；剪力包络图中，横轴为剪力与模型重量的比值(V/G).

2.1 塑性铰区数量对结构抗震性能的影响

图5和图6所示为地震作用下单塑性铰区模型与多塑性铰区模型的弯矩包络图，可以发现所有的单塑性铰区模型因受到高阶振型的影响，模型上部的弯矩远远大于底部弯矩，弯矩包络图的形状也与振型分解反应谱法得到的剪力墙结构弯矩包络图截然不同.多塑性铰区模型与单塑性铰区模型相比，由于在地震中通过多个塑性铰区的塑性变形，减小了高阶振型的影响，可以有效地控制模型上部的弯矩.不同数量多塑性铰区模型之间的弯矩图也有所不同，三塑性铰区模型和四塑性铰区模型与双塑性铰区模型相比，在模型底部和H/2高度处所受弯矩相差不大，但在其他部位因为有塑性铰区的耗能作用，弯矩显然比双塑性铰区模型更小.如图6中20层模型弯矩包络图所示，三塑性铰区和四塑性铰区模型底部弯矩均相对双塑性铰区模型减少8.3%，H/2高度处弯矩减少8.8%；而在H/3高度处，三塑性铰区模型承受弯矩比双塑性铰区模型减少38.6%，四塑性铰区模型承受弯矩比双塑性铰区减少45.8%.而三塑性铰区模型和四塑性铰区模型相比，两者弯矩包络图差别不大，甚至在图5中，三塑性铰区模型所受弯矩比四塑性铰区模型小.可见四塑性铰区模型相比于三塑性铰区模型，抗震性能并没有明显改善，主要原因是模型在地震中输入的能量有限，三个塑性铰区足以耗散模型所承受的地震能量.因此，不能简单地认为塑性铰区个数越多，结构地震内力越小.

图6 RIN228作用下单塑性铰区与多塑性铰区模型弯矩包络图Fig.6 Bending moment envelopes of single plastic hinge region and multi-plastic hinge region models for the record RIN228

图7和图8所示为地震作用下单塑性铰区与多塑性铰区模型的剪力包络图，可以发现，多塑性铰区模型比单塑性铰区模型承受的剪力更小，尤其是模型上部的剪力大幅减小，这是因为多塑性铰区减小了高阶振型的影响.对比多塑性铰区模型之间的剪力包络图可以看出，三塑性铰区模型和四塑性铰区模型较双塑性铰区模型上部剪力有少量的减小，而三塑性铰区模型和四塑性铰区模型承受的剪力差距不大.

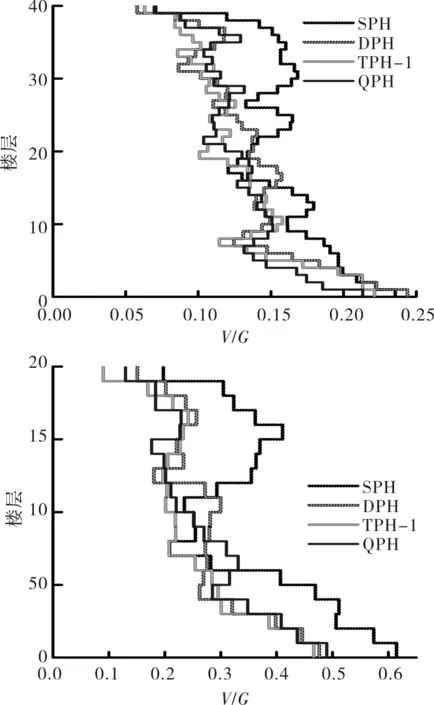
图7 BOL090作用下单塑性铰区与多塑性铰区模型剪力包络图Fig.7 Shear force envelopes of single plastic hinge region and multi-plastic hinge region models for record BOL090

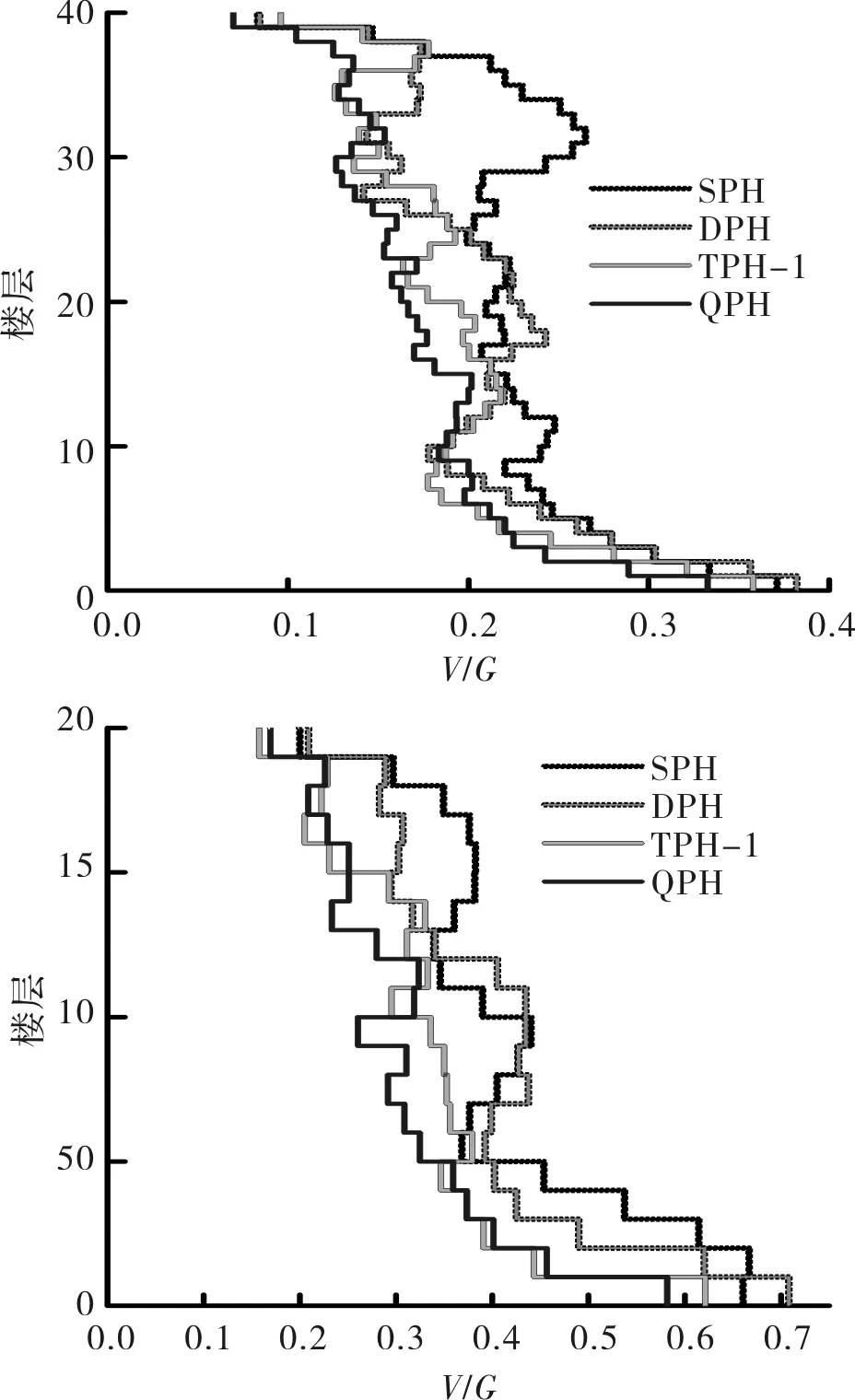
图8 RIN228作用下单塑性铰区与多塑性铰区模型剪力包络图Fig.8 Shear force envelopes of single plastic hinge region and multi-plastic hinge region models for record RIN228

2.2 塑性铰区位置对结构抗震性能的影响

三塑性铰区即可有效减小高阶振型效应，对3种三塑性铰区模型进行非线性时程分析.多塑性铰区布置形式C、D、E均包含三个塑性铰区，只是布置塑性铰区的位置不同.图9和图10所示为地震作用下不同布置形式的三塑性铰区模型的弯矩包络图，对比可以发现，形式D模型和形式E模型在上部的部分区段承受的弯矩大于底部弯矩，说明这两种形式没有完全地控制高阶振型效应，其中形式D模型下部弯矩有效减小，但是模型上部承受弯矩依然较大；形式E模型与其相反，模型上部弯矩小，而下部弯矩较大.形式C模型上部弯矩分布均匀，且均小于模型底部弯矩.这一现象在图10的40层模型弯矩包络图中尤为明显，形式D模型底部承受的弯矩略小于形式C模型，但是其上部的弯矩远大于形式C模型，在3H/4高度处所承受弯矩为其底部弯矩的1.3倍，为形式C模型相同位置弯矩的2倍；而形式E模型上部承受弯矩和形式C模型相近，但是模型下部弯矩较大，在H/3高度处承受弯矩是其底部弯矩的1.43倍，为形式C模型相同位置弯矩的1.8倍.因此可以得出：当塑性铰区集中在一个区段时，该区段的弯矩显著减小，而对距该区段较远的部分影响较小，故应当均匀地布置塑性铰区，避免出现局部受力过大的现象.

图11和图12所示为三种不同布置形式的三塑性铰区模型在地震作用下的剪力包络图，可以得出与弯矩包络图同样的规律，形式D、E只能在模型局部起到作用，而形式C可以使模型整体承受的剪力减小.例如在图12的40层模型剪力包络图中，形式D模型底部剪力比形式C模型减少9.4%，但其上部剪力大于形式C，在5H/6高度处的剪力为形式C模型相同位置剪力的1.54倍.形式E的模型上部剪力相对于形式C有小幅的减小，而其底部剪力为形式C模型的1.1倍，H/2高度处剪力为形式C模型相同位置剪力的1.28倍.三种不同布置形式模型的剪力包络图虽然差距不大，但还是可以看出形式C模型较其余两种模型受力更加合理.

因此，塑性铰区数目相同时，不同的塑性铰区布置位置将对结构抗震性能产生较大的影响，不合理的布置不但会使结构在地震中存在安全隐患，还会增加经济成本.

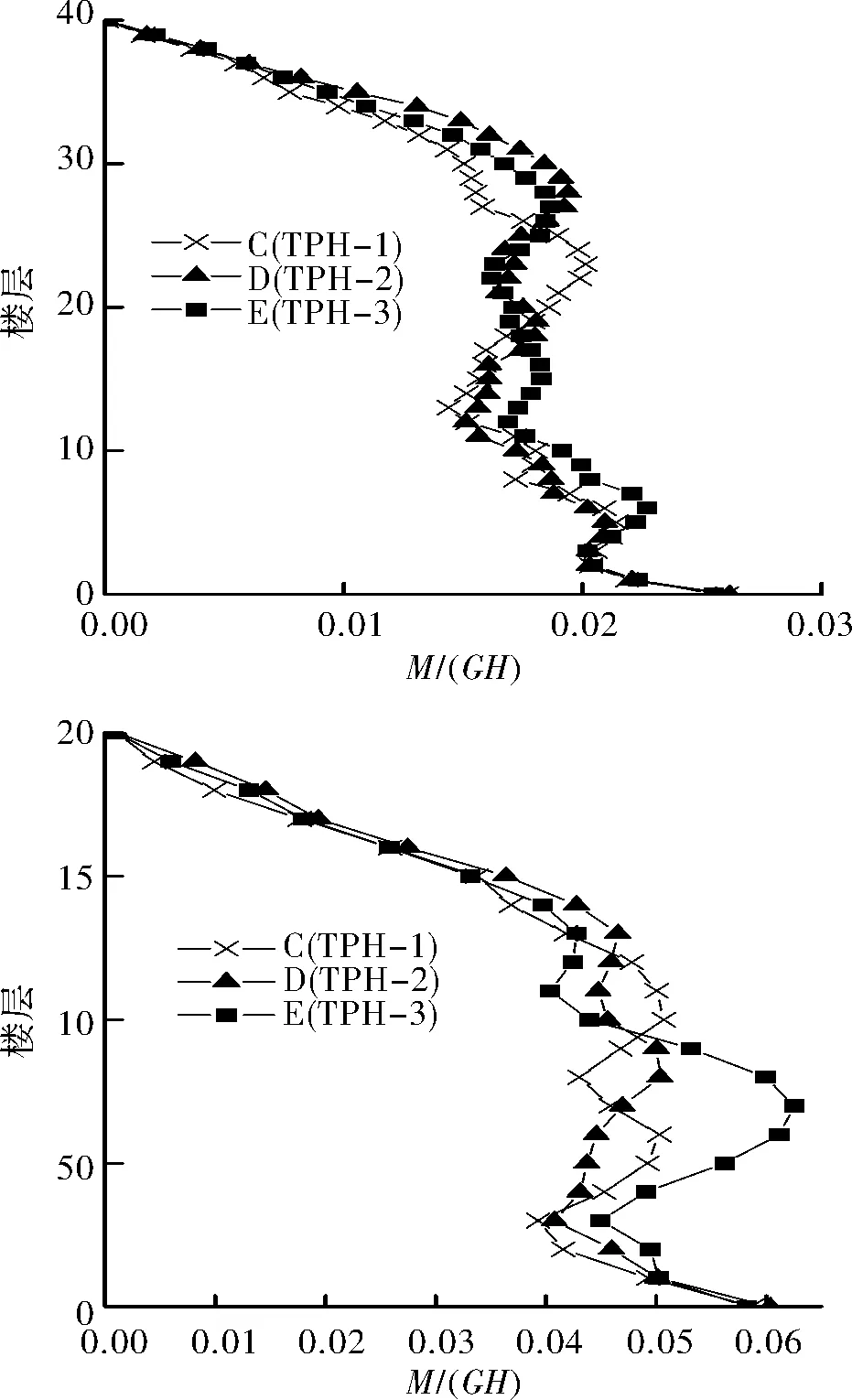
图9 BOL090作用下三塑性铰区模型弯矩包络图Fig.9 Bending moment envelopes of triple-plastic hinge region models for the record BOL090

图10 RIN228作用下三塑性铰区模型弯矩包络图Fig.10 Bending moment envelopes of triple-plastic hinge region models for the record RIN228

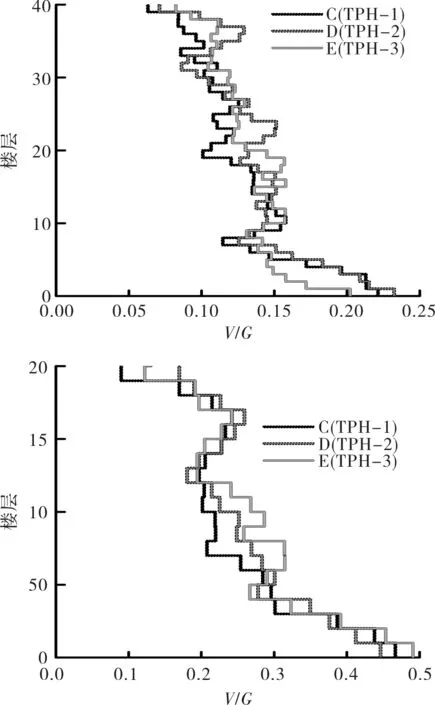
图11 BOL090作用下三塑性铰区模型剪力包络图Fig.11 Shear force envelopes of triple-plastic hinge region models for record BOL090

图12 RIN228作用下三塑性铰区模型剪力包络图Fig.12 Shear force envelopes of triple-plastic hinge models for record RIN228

3 结论

通过对比6种不同塑性铰区数量和布置位置的模型在罕遇地震作用下的受力情况，得出以下结论：

(1)多塑性铰区对于剪力墙结构高阶振型效应的减小程度是有限的，当塑性铰区数量超过三个时，结构在罕遇地震作用下的内力基本不变，即三个塑性铰区可最大幅度地减小结构在罕遇地震作用下的高阶振型效应.

(2)当塑性铰区数量一定时，不同的布置位置对模型在罕遇地震作用下的内力产生不同的影响，沿高度方向均匀布置的塑性铰区可以有效减小结构的地震内力.

(3)高烈度区剪力墙结构塑性铰区的合理布置是沿高度方向均匀布置三个塑性铰区.

[1] 中华人民共和国住房和城乡建设部.建筑抗震设计规范：GB 50011-2010[S].北京：中国建筑工业出版社，2010.

Ministry of Housing and Urban-Rural Development of People′s Republic of China. Code for seismic design of building: GB 50011-2010[S]. Beijing: China Architecture & Building Press,2010.

[2] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范：GB 50010-2010 [S]. 北京：中国建筑工业出版社，2010.

Ministry of Housing and Urban-Rural Development of People′s Republic of China. Code for design of concrete structures:GB50010-2010[S]. Beijing: China Architecture & Building Press,2010.

[3] 中华人民共和国住房和城乡建设部.高层建筑混凝土结构技术规程：JGJ 3-2010[S].北京：中国建筑工业出版社，2010.

Ministry of Housing and Urban-Rural Development of People′s Republic of China. Technical specification for concrete structures of tall building: JGJ 3-2010[S]. Beijing: China Architecture & Building Press,2010.

[4] KHEYRODDIN A, NADERPOUR H. Nonlinear finite element analysis of composite RC shear walls[J]. Iranian Journal of Science and Technology, Transaction B Engi-neering,2008, 32(2): 79-89.

[5] ESMAILI O, EPACKACHI S, MIRGHADERI R, et al. Rehabilitation of a high-rise coupled shear wall system in a 56-storey residential reinforced concrete building(Tehran Tower), based on nonlinear dynamic time-history analyses[J]. Structural Design of Tall and Special Buildings,2011, 20(8): 1035-1047.

[6] KLEMENCIC R,FRY J A,HOOPER J D,et al. Performance based design of ductile concrete core wall buildings issues to consider before detailed analy-sis[J].Structural Design of Tall and Special Build-ings,2007,16(5) : 599-614.

[7] MUNIR A, WARNITCHAI P. The cause of unproportionately large higher mode contributions in the inelastic seismic responses of high-rise core-wall build-ings[J]. Earthquake Engineering & Structural Dynam-ics,2012, 41(15): 2195-2214.

[8] HIEU Lu, IMAN Ghorbanirenani, PIERRE Léger, et al. Numerical modeling of slender reinforced concrete shear wall shaking table tests under high-frequency ground motions [J]. Journal of Earthquake Engineering, 2013, 17(4):517-542.

[9] Ghorbanirenani I, Tremblay R, Léger P, et al. Shake table testing of slender RC shear walls subjected to eastern North America seismic ground motions[J]. Journal of Structural Engineering,2011,138(12): 1515-1529.

[10] ZEKIOGLU A, WILLFORD M, JIN L, et al. Case study using the Los Angeles tall buildings structural design council guidelines: 40-storey concrete core wall building[J]. The Structural Design of Tall and Special Buildings, 2007, 16(5): 583-597.

[11] PANAGIOTOU M, RESTREPO J. Dual-plastic hinge design concept for reducing higher-mode effects on high-rise cantilever wall buildings[J]. Earthquake Engineering & Structural Dynamics, 2009, 38(12):1359-1380.

[12] Berkeley C A. PER-FORM-3D User guide[M]//Nonlinear analysis and per-formance assessment for 3D structures. Version 4. UC Berkeley:Computers and Structures, Inc. 2006.

[13] GRANGE S, KOTRONIS P, MAZARS J. Numerical modelling of the seismic behaviour of a 7-story building: NEES benchmark[J]. Materials and Structures, 2009, 42(10): 1433-1442.

[14] SCHOTANUS M I J, MAFFEI J R. Computer modeling and effective stiffness of concrete wall buildings[C]//Proceedings of the International FIB Symposium on Tailor Made Concrete Structures, Berlin:Research Gafe 2008,939-945.