非连续铺砂裂缝动态闭合实验
陈星宇 ,何昀宾 ,何封 ,尹丛彬 ,朱炬辉
(1.中国石油川庆钻探工程有限公司井下作业公司,四川 成都 610000;2.中国石油集团油田技术服务有限公司,北京 100007)
0 引言
致密砂岩气藏、页岩气藏等非常规储层,由于具有低孔、低渗的特点,开发过程中需通过水力压裂技术进行储层改造,才能获得工业气流[1-3]。大量室内研究及现场实践表明[4-5],受储层闭合压力、支撑剂颗粒嵌入及破碎等因素影响,压后支撑剂颗粒间隙压缩及残液滞留将大幅降低人工裂缝导流能力,导致改造效果不及预期。为确保压后可获得具有长期高效导流能力的支撑裂缝,通过高频交替注入支撑剂段塞与压裂液[6],改变缝内铺砂模式,形成不连续铺砂支撑裂缝,提高缝内孔道率[7],降低油气自人工裂缝向井筒的流动阻力,从而实现高产稳产的改造目标[8-11]。
郭建春等[12]通过开展纤维携砂室内模拟实验,发现纤维压裂液携砂性能主要取决于压裂液流变性及其微观结构。纤维-胍胶基液符合幂律流变模型,加入纤维可有效提高胍胶基液黏度,增加胍胶基液结构强度及内摩擦力,且分散于胍胶溶液中的纤维材料可形成三维网状结构,增加支撑剂颗粒包裹强度。B.HOU等[13]从闭合应力、弹性模量等现场敏感性参数出发,建立了优选泵注压裂液脉冲时间的参考模板,并分析了砂团间距对壁面稳定性的影响程度。X.J.ZHENG等[14]建立了缝内非连续铺砂模式下支撑裂缝渗透率计算模型,并基于赫兹接触理论及支撑剂嵌入几何尺寸,分析了缝内支撑剂砂团分散密度、支撑剂砂团半径等参数对裂缝导流能力的影响。钱斌等[15]从工艺原理、室内工程模拟评价及现场试验等方面展开研究,结果表明,较常规连续加砂压裂而言,脉冲式加砂压裂压后,产量得以大幅提升,同时可降低支撑剂用量,减少施工砂堵风险。
人工裂缝内支撑剂砂团能否保持一定大小孔道率是该项技术成功与否的关键,但针对裂缝动态闭合过程中支撑剂砂团稳定性及支撑缝宽变化规律等方面的相关研究较少。因此,笔者采用人工裂缝动态闭合模拟装置,研究缝内压裂液滤失条件下的裂缝动态闭合过程特征行为,并结合实验结果对相关特征参数进行表征与修正,目的是认识裂缝动态闭合对非连续铺砂裂缝缝内支撑剂砂团及相应特征参数的影响。
1 实验方案
根据非连续铺砂裂缝压后动态闭合过程原理,设计了一套脉冲式加砂压裂非连续铺砂裂缝压后动态闭合模拟实验系统,主要由液压动力输送系统、可视裂缝观测系统、高清视频采集系统、滤失液体回收系统、数据采集与控制系统等构成(见图1),其耐压可视裂缝观测系统如图2所示。液压泵加压,推动液压活塞缸内活塞上行,从而推动主体内活塞板上下,模拟裂缝动态闭合过程;在主体一侧装载压力传感器,测定缝内压力变化情况;在活塞板内表面开设滤失流动沟槽及滤失孔道,滤失孔道外接滤失管线及滤失液体计量器,通过电子位移计测量液压活塞缸内活塞上行距离,确定缝宽变化情况。

图1 非连续铺砂裂缝动态闭合模拟实验系统

图2 非连续铺砂裂缝动态闭合模拟实验装置结构组成
利用人造岩板模拟裂缝壁面。人造岩板几何尺寸为 40 cm×19 cm×3 cm,渗透率为 2.3×10-3μm2,弹性模量为20 GPa,泊松比为0.22;将现场常用20/40目低密度陶粒支撑剂配制成质量浓度为180~620 kg/m3的携砂液,压裂液破胶前黏度为160 mPa·s,压裂液中纤维质量浓度为2.1~3.1 kg/m3;设定初始缝宽为10 mm。
将不同质量浓度的携砂液以支撑剂砂团样式铺置于人造岩板上,并将压裂液充满整个模拟裂缝;在主体表面凹槽内采用密封圈实现玻璃板与主体上表面的接触密封,并通过螺栓将不锈钢视窗、可视玻璃板与主体间实现紧固密封;通过主体加持旋转系统,将人工模拟裂缝旋转至垂直裂缝状态,开启滤失通道,以阶梯方式向模拟裂缝加载闭合压力,并通过数据采集系统,记录裂缝动态闭合过程中支撑剂砂团缝内沉降及变形情况。
2 实验结果分析
脉冲式加砂压裂现场实施过程中,采用伴注纤维确保支撑剂段塞在运移过程中有效聚集不分散,即纤维质量浓度随携砂液质量浓度变化而变化。由于不同质量浓度携砂液段塞在纤维压裂液环境中遵循Kynch沉降定律[16-17],在缝高方向、相同质量浓度条件下,支撑剂砂团沉降速率相同,因此,携砂液质量浓度改变时,支撑剂砂团沉降规律不变,此处以携砂液质量浓度为500 kg/m3的实验结果为例进行分析。分别绘制累计滤失量、缝宽、缝内流体压力与裂缝动态闭合时间关系图(见图3、图4)。由图3所示,裂缝动态闭合过程有3个阶段。第1阶段:由于缝内流体仍保持一定压力,故滤失量较大,液体滤失速度及缝宽减小较快。第2阶段:由于缝内流体压力逐渐减小,此时滤失量较第1阶段略小,且滤失速度及缝宽减小速度均减缓,此阶段持续过程最长。第3阶段:由于滤失量累增到一定程度后,缝内流体压力接近忽略状态,此时裂缝壁面内外滤失压差较小,因此累计滤失量及裂缝宽度在数值上的变化也较小,整个裂缝闭合系统趋于稳定状态。

图3 累计滤失量、缝宽与闭合时间关系
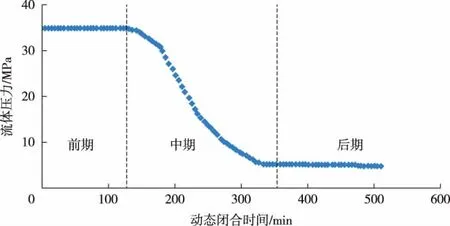
图4 缝内流体压力与闭合时间关系
由图4可知,随裂缝动态闭合时间增加,缝内流体压力也相应呈现出阶段性特征。裂缝动态闭合前期:由于缝内压裂液处于破胶前期,此时流体黏度仍较高,流动性较差,因此缝内流体压力降低速率较小,趋势平缓。裂缝动态闭合中期:液体破胶作用导致缝内流体黏度迅速下降,流动性增强,滤失量迅速增加,此时缝内流体压力迅速降低,且整体表现出先强后弱的变化趋势。监测数据表明,动态闭合中期,缝内流体压力降幅高达90%。裂缝动态闭合后期:由于液体滤失趋于平稳、无变化,此阶段缝内流体压力逐渐趋于稳定。
根据累计滤失量、缝宽及缝内流体压力等参数随动态闭合时间变化情况,结合缝内支撑剂砂团与缝宽的相对关系。将压后裂缝动态闭合过程划分为3个阶段,如图5所示。
裂缝动态闭合初期(t∈(0,t1))为缝内流体承压阶段。由于缝内压裂液尚未完全破胶,此时作用于裂缝壁面的闭合应力全部作用于缝内流体上,缝内外流体滤失压差较大,此阶段裂缝闭合主要受流体滤失量影响。裂缝初始宽度w0大于支撑剂砂团高度hp(△h1=w0-hp,△h1>0),支撑剂砂团将在缝高方向逐渐沉降,同时受缝宽逐渐减小影响,支撑剂砂团将在高度方向上压缩,径向扩展。
裂缝动态闭合中期(t∈(t1,t2))为承压过渡阶段。支撑剂砂团与裂缝壁面开始接触,此时hp与裂缝宽度wf相等。压裂液破胶后,流动性迅速增加,液体滤失量也随之增加。受地层温度场影响,人工裂缝内温度逐渐恢复至地层温度,此时支撑剂砂团在纤维包裹缠绕作用下逐渐固结,其在受压条件下的变形特征从前期类似于液体受压变形,过渡至固体受压变形范畴。在地层闭合压力作用下,其高度压缩、径向扩展程度将加剧,即由缝内流体主导、支撑剂砂团辅助承压,向支撑剂砂团主导、缝内流体辅助承压过渡。
裂缝动态闭合后期(t∈(t2,t3))为支撑剂砂团承压阶段。由于缝内液体滤失量逐渐趋于稳定,此时支撑剂砂团将承受绝大部分地层闭合压力作用,缝内流体承压可忽略。该阶段,支撑剂砂团将出现局部嵌入、破碎的现象,且缝内支撑剂砂团未支撑区域的裂缝壁面将出现弯曲变形(△hp′=hp-wf,△hp′>0),其后,非连续铺砂裂缝内部将趋于稳定状态。
3 特征参数表征
考虑支撑剂砂团沉降、缝内流体滤失、支撑剂砂团形变、裂缝未支撑区域壁面形变等因素的影响,推导脉冲式加砂压裂压后裂缝动态闭合过程中人工裂缝缝内孔道率及缝宽持有率等特征参数的数学表征。
3.1 缝内孔道率
由于支撑剂砂团在裂缝动态闭合前期仅发生沉降,其形态变化可忽略,因此选取单位脉冲泵注周期作为研究对象。
定义单位脉冲泵注周期内缝内流体面积占有百分比为缝内孔道率:
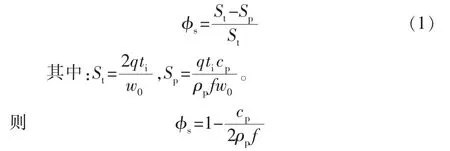
式中:φs为孔道率;St为单位周期内携砂液总面积,m2;Sp为单位周期支撑剂砂团总面积,m2;q为注入量,m3/s;ti为脉冲时间,s;cp为携砂液质量浓度,kg/m3;ρp为支撑剂密度,kg/m3;f为裂缝缝宽持有率(即裂缝动态闭合过程中动态缝宽与最大缝宽的百分比)。
3.2 缝宽持有率
根据人工模拟裂缝闭合实验特征及支撑剂砂团高度与裂缝缝宽的相对大小,将整个裂缝闭合过程划分为3个阶段。
由于裂缝动态闭合过程中,裂缝动态宽度在不同阶段受到压裂液滤失、砂团形变、砂团嵌入作用的影响程度不同,因此裂缝动态宽度是这3个影响因素的综合函数,同时也是整个研究阶段的分段函数。
对于滤失系数的注取,计算模型假设条件:1)压裂施工结束后裂缝不再发生扩展;2)缝内支撑剂砂团简化为圆柱状弹性体,与裂缝壁面发生接触挤压(即第2、第3阶段);3)在整个裂缝动态闭合过程中,一直存在缝内压裂液滤失,且根据实验测得累计滤失量的变化曲线,可知第3阶段的滤失量很小,此处忽略不计。
压裂液滤失主要受3种因素的控制,即压裂液黏度、地层流体及岩石的压缩性、压裂液的造壁性。压裂液滤失量以滤失系数表示[18-20]。
受压裂液黏度控制的滤失系数:

受地层流体及岩石压缩性控制的滤失系数:

受压裂液造壁性控制的滤失系数:
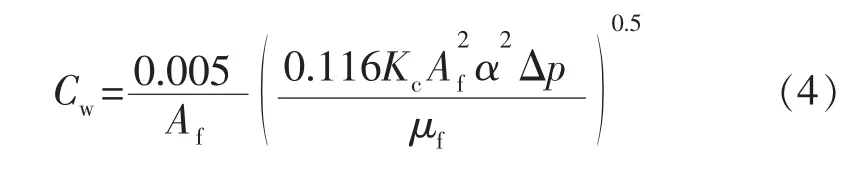
式中:Cv,Cc,Cw分别为受压裂液黏度、地层流体及岩石压缩性、压裂液造壁性控制的滤失系数,m·min-0.5;Kf,Kr,Kc分别为地层对压力液、地层对层流体、滤饼对压裂液的渗透率,μm2;φ为储层岩石孔隙度;△p为缝内外压差,MPa;μf,μr分别为压裂液、地层流体的黏度,mPa·s;Ct为综合压缩系数,MPa-1;Af为滤失面积,cm2;α为累计滤失量与所形成的滤饼体积的比例系数。
应用分压降法求得的综合滤失系数C可表示为

根据力平衡原理和体积守恒原理,各阶段的缝宽变化皆可利用压裂液滤失量等效求解,即以整个研究过程为对象,对影响裂缝动态缝宽的所有控制因素,如支撑剂砂团形变、裂缝壁面形变等对缝宽的控制作用均以滤失量表征。设从实验开始至第i时刻的压裂液滤失量为dV,则有:

式中:△t为实验开始至第i时刻时间,min。
根据体积守恒原理,单位时间内液体滤失量即模拟平板缝间体积变化量,若缝宽减小量为dh,则有:
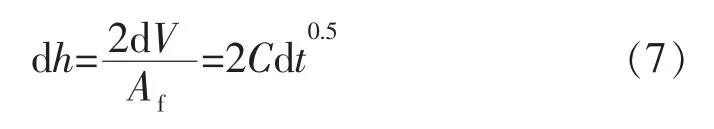
则第i时刻的缝宽持有率fi为
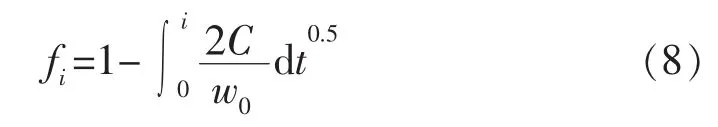
利用实测缝宽及滤失量数据,结合缝宽持有率计算方法,得到实际滤失系数Ca:

利用Ca对C进行拟合修正(见图6),得到修正后的综合滤失系数:
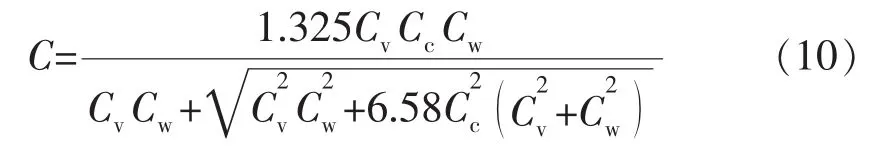

图6 压裂液综合滤失系数修正
4 裂缝参数修正
4.1 支撑剂砂团高度修正
由于脉冲式加砂压裂高频支撑剂段塞依靠纤维分散形成的三维网状结构对支撑剂颗粒形成包裹缠绕,提高了支撑剂段塞流动的稳定性,确保段塞进入人工裂缝后有效聚集不分散,但其内在力学作用机理尚未明确。分析动态闭合沉降模拟实验实测缝宽动态变化数据可知,分均匀铺置支撑剂砂团缝内形变近似弹性形变特征。定义支撑剂砂团综合压缩系数为Ctp,则可得支撑剂砂团受力条件下形变体积及形变高度计算表达式:
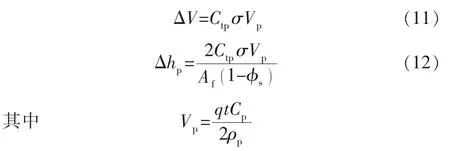
式中:σ为作用于支撑剂砂团上的有效闭合应力,MPa;△V 为支撑剂砂团形变体积,m3;△hp为支撑剂砂团形变高度,m;Vp为支撑剂砂团体积,m3。
利用动态砂团形变高度数据拟合求解(见图7)得Ctp=1.508×10-2MPa-1。 代入式(12)可得:


图7 支撑剂砂团形变高度修正
4.2 裂缝形变量修正
室内实验研究表明,当支撑剂砂团受到的单位面积应力超过一定大小后,其主要形变基本结束,后期随应力增加砂团形变量极小。因此支撑剂砂团的嵌入作用可以视为刚性体对裂缝壁面的加载。根据K.L.Johnson关于弹性半空间内点载荷作用条件下接触面变形理论有:

式中分别为模的第2类完全椭圆积分为模的第1类完全椭圆积分;uz为形变量,mm;E为弹性模量,MPa;a为砂团受压扩展后的半径,mm;r为形变计算点距离砂团的中心距离,mm;ν为泊松比。
综合式(14)、式(15),将支撑剂砂团中心到边界的平均嵌入量△hf视为该阶段的裂缝动态形变量,则有:

根据实验实测裂缝形变量,修正K.L.Johnson理论模型(见图8)。修正系数为0.885,修正后裂缝形变量计算公式为
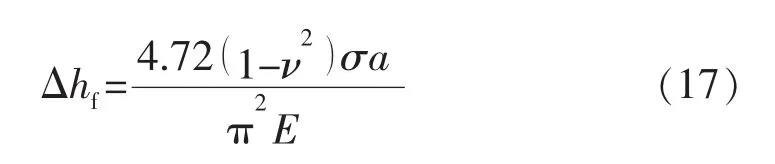

图8 非连续铺砂裂缝形变量修正
4 结论
1)根据承压载体差异,可将非连续铺砂裂缝压后动态闭合过程分为缝内流体承压阶段、承压过渡阶段及支撑剂砂团承压阶段,各阶段主控因素分别为流体滤失、支撑剂砂团受压形变、局部嵌入破碎。压后动态闭合过程中,裂缝宽度及累计滤失量随闭合时间变化均呈现出前期平缓、中期激增、后期平缓的特征。
2)结合压裂设计参数推导的缝内孔道率及缝宽持有率数学表征式,可用于描述非连续铺砂裂缝缝内孔道率及动态缝宽,且缝内孔道率与动态缝宽密切相关,缝宽持有率越大,缝内孔道率越小。
3)根据实验数据修正的滤失系数、支撑剂砂团高度及裂缝形变量计算公式,可为非连续铺砂压裂参数优化设计、获取最优缝内孔道率提供参考。随动态闭合压力增加,缝内支撑剂砂团嵌入量,即裂缝形变量逐渐增加,后期趋于平缓。
[1]侯冰,陈勉,程万,等.页岩气储层变排量压裂的造缝机制[J].岩土工程学报,2014,36(11):2149-2152.
[2]HOU B,CHEN M,WANG Z,et al.Hydraulic fracture initiation theory for a horizontal well in a coal seam[J].Petroleum Science,2013,10(2):219-225.
[3]侯冰,谭鹏,陈勉,等.致密灰岩储层压裂裂缝扩展形态试验研究[J].岩土工程学报,2016,38(2):219-225.
[4]PYRAK-NOLTE L J.The seismic response of fractures and the interrelationships among fracture properties[J].International Journal of Rock Mechanics Mining Science&Geomechanics Abstracts,1996,33(8):785-802.
[5]EJOFODOMI E,CAVAZZOLI G,MORRIS J,et al.Application of channelfracturingintheVacaMuertaShaleFormation[R].SPE169383,2014.
[6]GILLARD M,MEDVEDEV O,PENA A,et al.A new approach to generating fracture conductivity[R].SPE 135034,2010.
[7]TINSLEY J M,WILLIAMS J R.A new method for providing increased fracture conductivity and improving stimulation results[J].Journal of Petroleum Technology,1975,27(11):1319-1325.
[8]RHEIN T,LOAYZA M,KIRKHAM B,et al.Channel fracturing in horizontal wellbores:the new edge of stimulation techniques in the eagle ford formation[R].SPE 145403,2011.
[9]AHMED M,HUSSAIN A,AHMED M.Optimizing production of tight gaswellsbyrevolutionizinghydraulicfracturing[R].SPE141708,2011.
[10]YUDIN A,TARAKANOV I,KLYUBIN A,et al.Channel fracturing improves stimulation efficiency by 30%in the Achimov Gas Condensate Formation[R].SPE 171324,2014.
[11]SHARMA A,SHAH A,BORDEORI K,et al.Channel fracturing maximizes production from low-permeability reservoirs in India [R].SPE 178108,2015.
[12]郭建春,高阳,赵志红,等.脉冲纤维压裂液携砂机理[J].石油钻采工艺,2016,38(1):88-92.
[13]HOU B,ZHENG X J,CHEN M,et al.Parameter simulation and optimization in channel fracturing[J].Journal of Natural Gas Science&Engineering,2016,35(A):122-130.
[14]ZHENG X J,CHEN M,HOU B,et al.Effect of proppant distribution pattern on fracture conductivity and permeability in channel fracturing[J].Journal of Petroleum Science and Engineering,2016,149(A):98-106.
[15]钱斌,尹丛彬,朱炬辉,等.高效脉冲式加砂压裂技术研究与实践[J].天然气工业,2015,35(5):39-45.
[16]TILLER F M.Revision of Kynch sedimentation theory[J].American Institute of Chemical Engineers Journal,1981,27(5):823-828.
[17]刘玉婷,管保山,刘萍,等.纤维对压裂液携砂能力的影响[J].油田化学,2012,29(1):75-79.
[18]李勇明,郭建春,赵金洲,等.裂缝性气藏压裂液滤失模型的研究及应用[J].石油勘探与开发,2004,31(5):120-122.
[19]李勇明,郭建春,赵金洲,等.裂缝性储层压裂液滤失计算模型研究[J].天然气工业,2005,25(3):99-101.
[20]付永强,郭建春,赵金洲,等.一种多参数的压裂液在双重介质中滤失模型的推导与计算[J].天然气工业,2003,23(3):88-91.

