牵引变流器二次谐振回路对系统性能影响的研究

夏梁志，刘 雄，韩乔琳，陈 鑫

（1. 中车永济电机有限公司，山西永济 044502；2. 南非中车永济电机有限公司，南非德班）

牵引变流器采用背靠背式的交-直-交变流器结构，能够将受电弓传送的单相定频交流电变换为三相变频变压的交流电供给牵引异步电机，从而驱动机车运行[1]。电力机车牵引变流器的整流部分通常采用单相 PWM 整流，尽管通过适当的控制可以使该整流器无论工作在整流状态或者逆变状态系统均可以获得极高的功率因数，然而由于单相 PWM 整流器的控制特性，将不可避免地导致直流侧会含有 2 倍电网频率的电压纹波[2-3]。该直流二次纹波电压不仅会引起直流母线电压的剧烈震荡，容易造成变流器过压故障，还会产生拍频电流，造成电机温升极限超标和低频脉动转矩，阻碍机车正常运行[4-6]。因此，对直流母线电压二次脉动抑制的研究具有重要的现实意义。

对于单相整流造成的直流电压脉动，一般有硬件滤波和软件滤波两大类方法。在变流器的设计中，一般采取的方案是在牵引变流器直流侧并联容值较大的支撑电容，或者通过设计合适的谐振频率为 100 Hz 的二次滤波回路来抑制直流电压纹波。目前，国内的 CRH2、CRH5 型动车牵引变流器均采用直流侧并联大电容方式来抑制母线电压二次脉动影响[7]，而 CRH1、CRH3 型动车以及复兴号 CR400BF 型动车牵引主变流器则采用在直流侧并联二次滤波电路的方法。

交-直-交传动系统的直流回路一般包括 2 个部分：一个是支撑电容器；另一个是二次串联谐振电路[8]。针对牵引系统运行时中间直流环节将产生二次电压脉动的现象，首先分析其产生原因，然后给出抑制其二次电压脉动的直流侧支撑电容的设计方法及二次谐振滤波元件的选取方法，最后通过搭建仿真模型以及高压系统试验，研究二次谐振滤波回路对系统性能的影响。

1 直流侧串联谐振电路设计

1.1 二次电压纹波产生机理

典型单相 PWM 整流器的主回路原理如图 1 所示。图 1 中虚线框内的二次滤波电感 L2和二次滤波电容 C2构成串联谐振回路，uN为变压器二次侧等效电源电压，iN为变压器二次侧电流基波，即整流器的输入电流。LN和 RN分别为折算到二次侧的牵引变压器绕组的等值漏感和电阻。uab为经控制生成的四象限整流器输入 PWM 波电压，ud为中间直流母线电压，idc为整流器输出直流电流，idc2为中间直流环节二次滤波回路电流。Cd为中间支撑电容，RL为负载电阻。

图1 单相 PWM 整流器主回路原理图

因图 1 所示电路的工作特性，通过控制可以使其交流侧功率因数为 1 或者接近于 1[9]，在忽略开关管的功率损耗情况下，整流器交流侧输入功率应当与直流侧输出功率近似相等，即：

假设变压器二次侧等效电源电压：

式（2）中，UN为电压 uN的有效值，ωN为基波角频率，t 为时间。

由于单相整流器功率因数近似为 1，则变压器二次侧电流基波可表示为：

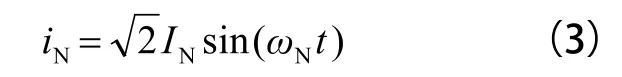
式（3）中，IN为电流iN的有效值。

由于直流母线电压幅值远大于二次脉动电压变化幅值，因此，可假定直流母线电压 ud为一恒定直流量 Ud，即：

图2 给出了单相整流器工作在整流工况的相量关系图，其中 φ 为经调制后的四象限整流器输入电压与二次侧电源电压的夹角。

根据图2整流工况相量图可知：

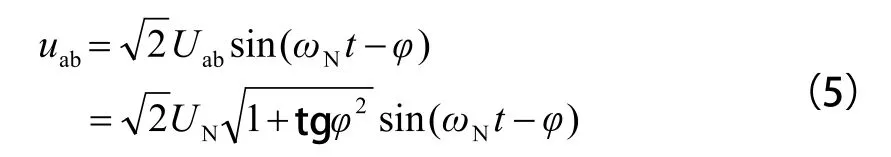
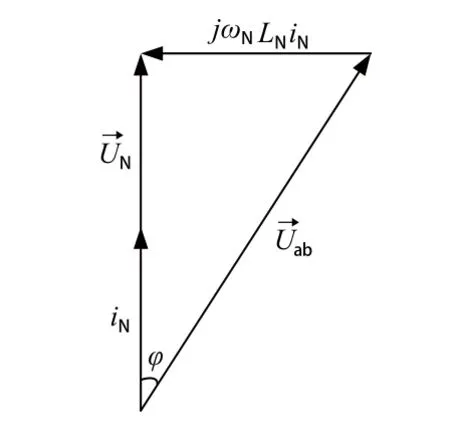
图2 整流工况的相量图

式（5）中，Uab为 uab中基波有效值，由式（1）、（2）、（3）、（4）、（5）可以推得：

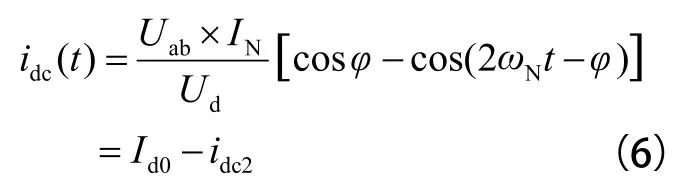
其中：

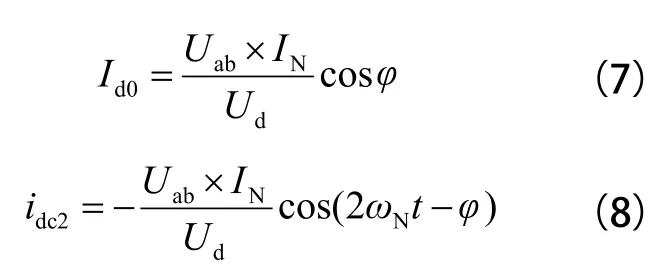
从式（6）可知，单相 PWM 整流器的输出电流 idc（t） 由两部分组成，除了直流分量 Id0外，还包含一个交流分量 idc2，其频率为电网频率的 2 倍。由于此交流分量的存在，整流器输出电压将产生 2 倍电网频率的二次脉动电压。在工程设计中，在整个系统对中间母线电压波动范围要求不高或者负载功率不大等情况下，可以采用增大直流侧支撑电容的方法抑制二次纹波。但如果直流侧二次脉动电压对系统性能产生明显影响，就必须采用二次谐振回路来满足系统性能要求，如图 1 中虚线框所示。

1.2 直流侧中间支撑电容设计

在牵引电传动系统中，直流侧支撑电容作为中间直流环节的储能器起着非常重要的作用。一方面它可以补偿电机的无功功率，改善电机的输出性能。另一方面，还可补偿系统负载突变造成的能量损失，使中间直流电压保持稳定，同时还可抑制高次谐波。因此，支撑电容的设计在中间直流环节非常重要。

由式（6）可知，单相 PWM 整流器的输出电流idc(t) 由一个恒定分量和一个以 2 倍供电频率脉动的交流分量构成。因此，直流分量将全部流入负载，而交流分量则流入由 L2和C2串联构成的串联谐振电路中，则可得如下关系式：

式（9）中，Idc2为二次谐波电流分量的有效值，Id0为直流分量的有效值。

在系统工作稳定时，系统的静态功率平衡，可表示为：

综合式（9）、（10）可得：

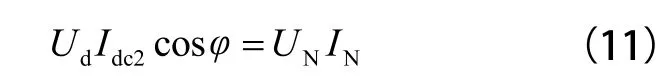
假设由二次谐波电流引起的脉动电压为 U2，并且二次脉动电压 U2波动的振幅为中间直流电压 Ud的 λ 倍，可表示为 U2= λUd，则可得：

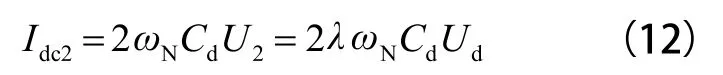
由式（11）、（12）可以推得中间支撑电容计算公式：

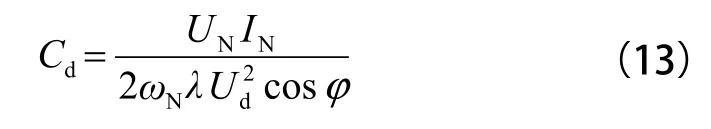
式（13）中，UN、IN分别为单相整流器输入电压、电流有效值；λ 为允许的二次谐波电压波动范围。

由式（13）可知，中间支撑电容 Cd是由系统输入功率、直流母线电压以及网压频率等因素共同决定的，并且与二次脉动电压的波动范围 λ 成反比，系统滤波效果亦对参数变化不敏感。因此，在直流侧并联大容量的支撑电容对于减小二次脉动功率的影响是直观可行的。

1.3 直流侧串联谐振电路设计

LC 滤波器是一种常用的有效抑制直流母线二次脉动影响的方案，基本原理是通过设计合适的 LC 滤波回路，选择准确的元件参数，使得 LC 回路的谐振频率为电网电压频率的 2 倍，形成对二次脉动电流的零阻抗通路，理论上可以完全滤除二次脉动电压[10]。因其结构简单、经济方便，在机车、动车牵引领域得到了广泛应用。因此，正确的 LC 滤波回路设计对牵引变流器性能将产生重要影响。

这里首先确定滤波回路中 L2、C2的额定工作电流，即为二次谐波电流的有效值。由式（6）、（8）可以得到其额定工作电流有效值为：

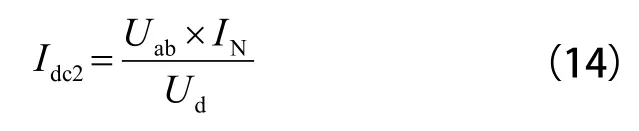
其次确定二次滤波电容 C2和电感 L2的最高工作电压值，即：

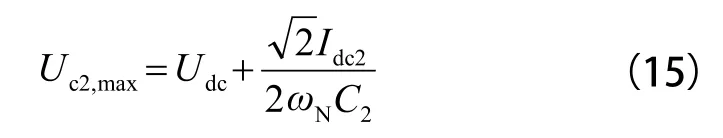
式（15）中，Udc为支撑电容两端直流电压有效值，串联谐振滤波回路 L2、C2的容量应根据下列关系式确定：

一般变流器设计中，应尽可能先确定电容 C2的值，再根据公式（16）确定电感 L2的值。从系统的稳定性考虑来看，C2的值尽可能选的要大，但是一般电容值越大，其体积也越大，成本越高。在牵引变流器中，C2一般采用金属化薄膜电力电容器，由于其成本高，所以要求的值又尽可能小。另外，为降低谐振电路参数偏移对滤波效果的影响，设计电路时常选取较大的直流母线支撑电容和 LC 电路配合使用。一般设计中先确定电容器的工作电压，再根据式（14）、（15）选取合适的电容值，最后由电容值进一步确定电感值。

2 仿真分析研究

计算机仿真采用美国 MathWorks 公司开发的MATLAB 软件。以目前在国内某种已运营的电力机车牵引传动系统为例，利用 Simulink 模块按照图 1 搭建仿真主电路模型，整个仿真系统由主电路以及控制部分组成。采用本文提出的设计方法分别计算中间支撑电容值、LC 滤波回路的电容值以及电感值并代入仿真模型，并采用有二次谐振回路的主回路和取消二次回路的主电路模型分别进行仿真。仿真过程中，设定输入电压为 AC950V、50 Hz，直流输出电压为 1 800 V，负载1 200 kW。控制器采用电压外环和电流内环相结合的双闭环控制方式，仿真模型的主要参数见表 1。

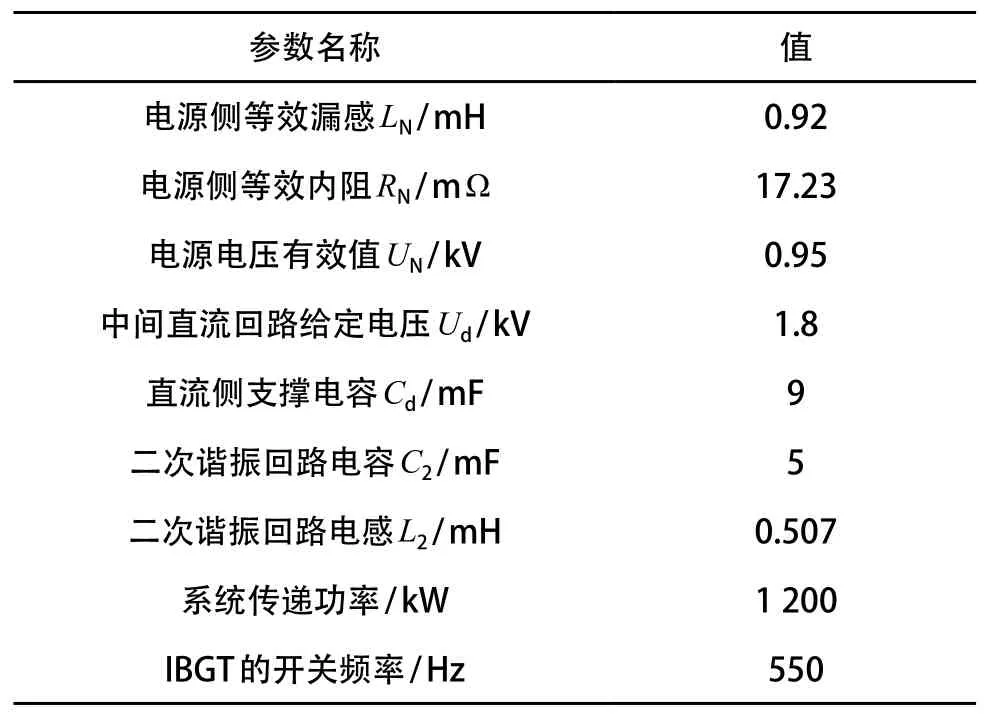
表1 仿真系统采用的基本参数

图3 分别给出了取消二次滤波回路和采用本文方法设计的二次滤波回路的四象限整流中间母线电压仿真波形和 10 倍频以下谐波电压分量比。

从图 3 可以看出，在无二次谐波抑制下，中间母线电压波动剧烈，且电机负载功率越大，波动越剧烈，并且中间母线电压存在明显的二次及 2 的倍频次的谐波，其中以二次脉动为主，高次谐波含量较少。而有谐波抑制下的中间母线电压波动较小，二次脉动电压明显得到抑制。

仿真结果表明，通过选择准确的参数设计的二次谐振回路，能明显地抑制直流侧二次脉动电压幅值，降低直流电压谐波含量。

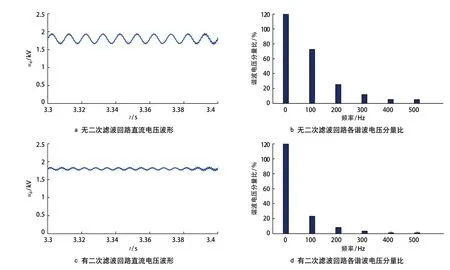
图3 仿真波形及各谐波含量对比

3 系统试验研究

牵引系统高压试验采用联调实验平台，其基本原理是：牵引变压器将电网的工频 25 kV 单相交流电经降压后供给牵引变流器，再通过 PWM 整流器及牵引逆变器向三相异步电动机提供可变压变频电源。牵引电机制动时的能量通过负载端的四象限变流器和整流变压器回馈至 10 kV 电网。图 4 给出了系统联调试验原理图。

图4 系统联调试验原理图

这里仍以上述电力机车牵引传动系统为例，采用的试验参数与仿真系统基本一致，电机转速为 1 260 r/min。图 5、图 6 分别给出了取消二次滤波回路和采用二次滤波回路的牵引系统高压试验波形图。

图5 取消二次滤波回路波形图

在图 5 中，1-3 绿色线 定义为直流母线电压，图 6 中2-2 线 为二次滤波回路电流。由图 5可知，牵引系统直流母线电压建立后，启动逆变器投入电机负载，负载越大，母线电压振荡越剧烈，振幅约为 280 V。图 6 显示牵引系统采用参数选取方法设计的二次滤波回路，系统到达满功率后依然运行稳定，母线电压波动很小，且可观察到频率为 100 Hz 的二次滤波电流流过二次谐振回路，试验结果与仿真分析一致。

图6 采用二次滤波回路波形图

4 结论

牵引变流器由于采用单相脉冲整流器，因而在其直流母线侧必然会产生二次纹波电压。直流二次纹波电压对牵引逆变器及牵引电机将会产生不利影响。通过仿真分析与系统高压试验结果的一致性，说明通过选取合适的电容、电感等参数设计的二次谐振回路，能有效地抑制直流侧母线电压二次纹波，稳定中间电压，提高牵引系统运行的稳定性。

[1]张大勇. 我国机车电传动技术的发展[J]. 机车电传动，2007（3）：1-4.

[2]郑俊，冯晓云，谢望玉，等. 单相PWM整流器瞬态电流控制策略的研究[J]. 电力电子技术，2009，43（12）：2-3，6.

[3]欧阳晖，张凯，张鹏举，等. 牵引变流器直流母线电压脉动下的无拍频电流控制方法[J]. 电工技术学报，2011，26（8）：14-23.

[4]J. Klima, M. Chomat, L. Schreier. Analytical closedform investigation of PWM inverter induction motor drive performance under DC bus voltage pulsation[J].IET Electric Power Applications, 2008, 2（6）：341-352.

[5]J. Klima. Analytical closed-form solution of a spacevector modulated VSI feeding an induction motor drive[J]. IEEE Transactions on Energy Conversion,2002, 17（2）：19l-196.

[6]陈燕平，忻力，李中浩. 单相电压型脉冲整流器中二次谐振电路的研究[J]. 机车电传动，2010（2）：28-32.

[7]张立伟，黄先进，游小杰，等. 欧洲主力交流传动机车主牵引系统介绍[J]. 电工技术学报，2007（7）：186-190.

[8]李伟，马志文，蔡华斌，等. 无二次滤波环节的单相四象限整流器输入电流控制研究[J]. 铁道学报，2014，36（5）：28-32.

[9]T. Shimizu, K. Wada, N. Nakamura. Flyback-type single-phase utility interactive inverter with power pulsation decoupling on the DC input for an AC photovoltaic module system[J]. IEEE Transactions on Power Electronics，2006，2l（5）：1264-1272.

[10]Akira Kimura. Frequency domain analysis of beatless control method for converter-inverter driving systems applied to AC electric cars[J]. Electrical Engineering in Japan，2010，174（4）：51-57.