一类具有领导者的群集运动分析

王庆亮,孔祥智,吴晨



一类具有领导者的群集运动分析

王庆亮,孔祥智,吴晨

江南大学理学院, 江苏 无锡 214122

本文主要研究了多智能体系统中具有领导者的群集运动。利用李雅普洛夫稳定性和比较定理，证明了跟随者与领导者之间的耦合系数足够大，系统能在任意给定的初始条件下达到群集运动。

群集运动; 领导者; 李雅普洛夫

智能体是指能感受到周围信息并能对自身做出相应调整的个体。例如每只鸟，每条鱼，每个人都是智能体。近年来，越来越多的文献开始涉及多智能体系统[1-5]。自然界中有很多生动有趣的群集现象，例如大雁成群结队的南飞，鱼类的群游和蚁群的聚集等等，我们将此类现象统称为群集运动。在这些群集运动中，各个智能体之间如何互相合作完成任务这一问题吸引了来自生物学，数学，人工智能学和计算机科学等领域学者的兴趣[6-8]。1986年，Reynolds[9]提出了群集运动的三条规则。这三条规则分别是：（1）速度匹配；（2）聚合规则；（3）分离规则。这对以后群集运动的研究具有深远的指导意义。它通常定义为当系统满足：（1）当时间趋于无穷时，智能体之间的速度差趋于0；（2）智能体之间的位移差趋于一个常数。我们就说智能体达到群集运动。

Cucker和Smale考虑的是无领导者的情形，但在现实生活中，会有领导者和跟随者的情形。例如在2017年8月13日，深圳地铁1号线上一名乘客因为上班迟到突然跑动，带动整节车厢的乘客全部跑动。这其实可以看成一个领导跟随者的群集运动。根据这种情形，本文建立数学模型并给出了达到群集运动的充分条件。

1 模型描述

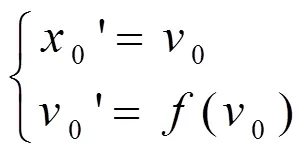
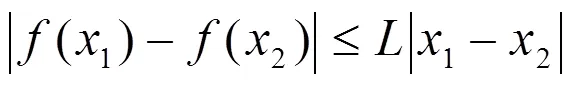
其中为利普西茨常数。

,=1,2,…,

其中，是耦合强度。

定义2.1[10]对于1≤≤，若系统(3)中的状态x，v满足：

2 带有领导者的群集运动

定理3.1：若系统（3）中的耦合强度大于函数的利普西茨常数，则系统（3）可以达到群集运动。

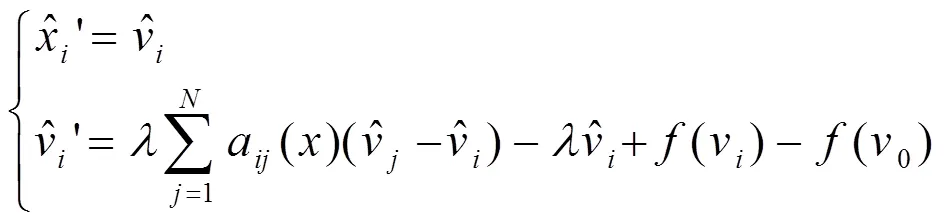
根据数列求和的性质，我们有：

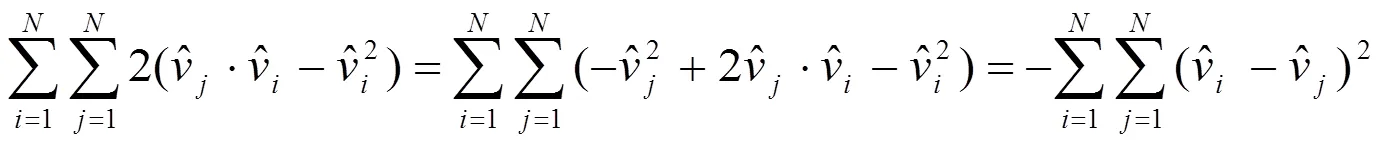
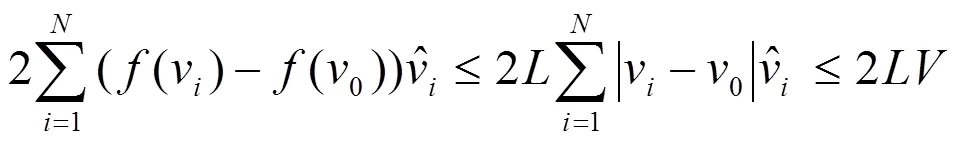
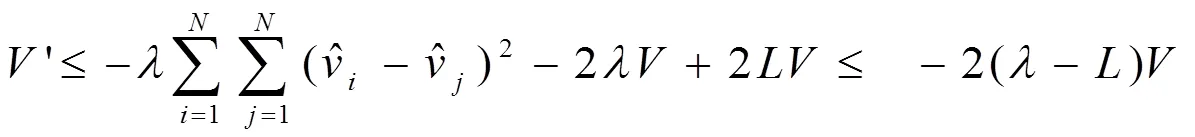
其中是一个常数。

根据（10）和（11）可知系统（4）达到群集运动。

证毕。

3 数值仿真

本节利用MATLAB四阶龙格库塔方法进行仿真，举出具体的例子来验证结论的正确性。本节选取八个跟随着的多智能系统进行分析。其中(0,0)=(80,12)，(1,1)=(24,19)，(2,2)=(45,16)，(3,3)=(46,15)，(4,4)=(78,7)，(5,5)=(98,8)，(6,6)=(88,14)，(7,7)=(68,10)，(8,8)=(39,9)，其中()=sin，则利普西茨常数=1。我们取=0.3。

定义两个新的函数来描述系统中速度和位移的动态过程：

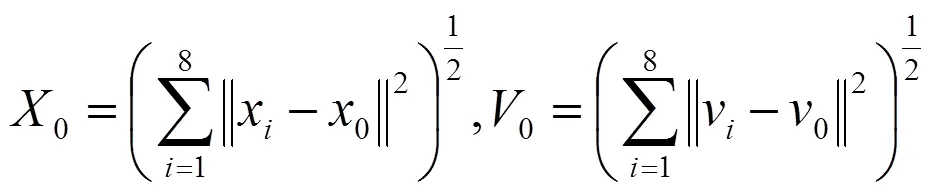
考虑在时间20 s内，当0≤0.01时，我们就认为速度达到一致。

例1当耦合系数=0.5时，对该系统进行仿真所得速度与位置误差数据如下（图1）。

图 1 误差数据

函数的利普西茨常数是1，当=0.5，也就是<,没有满足我们定理中的条件。从MATLAB仿真中（图1 (a)）可以看出，速度误差在20 s内没有趋于0，即没有达到群集运动。

例2耦合系数=1时，对该系统进行仿真所得速度与位置误差数据如下（图2）

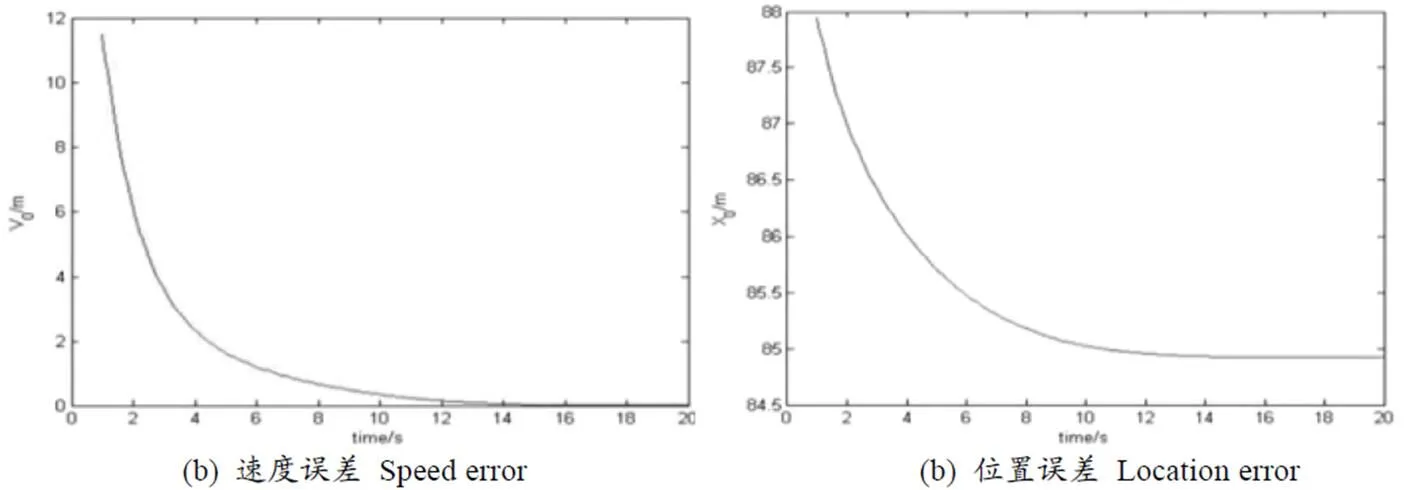
图2 误差数据

当=1时，即=时，由图2(a)可以看出，系统最终速度差趋于0，图2(b)位移差趋于一个常数，即系统达到群集运动。并求出速度达到一致的时间为0=15.9162。

例3耦合系数=2时，对该系统进行仿真所得速度与位置误差数据如下（图3）

图3 误差数据

当=2时，即>时，由图3(a)可以看出，系统最终速度差趋于0，(b)位移差趋于一个常数，即系统达到群集运动。并求出速度达到一致的时间为0=3.0366。

由例1，例2和例3的比较看出，当耦合系数比较小，小于函数的利普西茨常数时，系统达不到群集运动。当耦合系数大于等于利普西茨常数时，群集运动会出现，并且由上述的仿真结果可以得到，耦合系数越大，速度达到一致的时间越短。

[1] Tian Y, Liu C. Consensus of multi-agent systems with diverse input and communication delays[J]. IEEE Transactions on Automatic Control, 2008,53(9):2122-2128

[2] Liu C, Liu F. Stationary consensus of heterogeneous multi-agent systems with bounded communication delays[J]. Automatica, 2011,47(9):2130-2133

[3] Lin P, Jia Y. Average-consensus in networks of multi-agents with both switching topology and coupling time-delay[J]. Physica A: Statistical Mechanics and its Applications, 2008,387(1):303-313

[4] Olfati-Saber R. Flocking for multi-agent with a virtual leader[J]. IEEE Transactions on Automatic Control, 2006,51:401-420

[5] Tian Y, Liu C. Robust consensus of multi-agen systems with diverse input delays and asymmetric interconnection perturbations[J]. Automatic, 2009,45(5):1437-1353

[6] Xiao F, Wang L. Consensus protocols for discrete-time multi-agent systems with time-varying delays[J]. Automatica, 2009,45(5):1347-1353

[7] Ben-Jacob E, Cohen I, Czirók A,. Chemomodulation of cellular movement, collective formation of vortices by swarming bacteria, and colonial development[J]. Physical A: Statistical Mechanics and Its Applications, 1997,238(1-4):181-197

[8] Reif J, Wang H. Social potential fields: A distributed behavioral control for autonoomous robots[J]. Robotics and Autonomous Systems, 1999,27:171-194

[9] Vicsek T, Czirók A, Farkas IJ,Application of statistical mechanics to collective motion in biology[J]. Physical A: Statistical Mechanics and its Applications, 2015,274(1-2):182-189

[10] Fax JA, Murray RM. Information flow and cooperative control of vehicle formations[J]. IEEE Transactions on Automatic Control, 2004,49(9):1465-1476

Analysis on a Class of Flocking Motion with a Leader

WANG Qing-liang, KONG Xiang-zhi, WU Chen

214122,

This paper mainly studied the flocking motion with a leader in multi-agent system. By using Lyapunov stability and comparison theorem, the article proved that the coupling coefficient between followers and leaders was large enough and the system could achieve the flocking motion under any given initial conditions.

Flocking motion; leader; Lyapunov

TP273

A

1000-2324(2018)03-0547-04

2017-03-10

2017-04-02

王庆亮(1991-),男,硕士研究生,研究领域为模糊代数. E-mail:wangqingliang91@163.com