基于量子粒子群优化的DV-Hop算法研究

张中芳，张玲华

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003； 2.江苏省通信与网络技术工程研究中心，江苏 南京 210003)

0 引 言

随着计算机技术的发展，智能算法在最优化问题中的应用越发普遍，研究者们借助计算机的智能算法来有效地解决问题。通过采用一些新的搜索模型，并根据自然界的进化演变规律进行算法研究。研究者从基本的启发式算法出发，提出了群体智能算法。它是一种模拟自然过程的优化算法，如蚁群算法、粒子群算法等，因此在智能控制、电力系统和工程设计等方面应用广泛。无线传感器网络(wireless sensor network,WSN)[1]由大量的传感器节点组成，具有获取数据、处理信息和无线通信的能力，从而用来采集、处理和传输监测对象的信息。节点定位技术是无线传感器研究领域的关键技术，广泛应用于目标检测、目标识别和目标跟踪中。文中提出了一种改进量子粒子群算法与DV-Hop[2]算法的融合算法，有效改善了DV-Hop算法的节点定位误差，提高了定位精度。

1 DV-Hop定位算法的误差分析

DV-Hop算法是通过泛洪通信方法来记录节点之间的跳数和基于距离矢量路由协议的APS定位算法。DV-Hop定位算法一般分为三步，第一步计算各个节点之间的跳数，第二步根据跳数和信标节点之间的距离计算出平均跳距，第三步未知节点可以根据跳数和平均跳距计算出与信标节点之间的距离。通过这些有用的信息，利用三边测量法[3]或极大似然估计法[4]估计求得未知节点的位置坐标。

在经典的DV-Hop节点定位算法中，对未知节点位置估计的误差主要包括两个方面：一方面是平均跳距的估计形成的，采用的做法是直接利用锚节点之间的实际距离除以锚节点之间总的跳数所得；另一方面是用基本位置估计方法计算未知节点位置时产生的误差。文中研究的思路是使未知节点的估计坐标误差更小，对估计坐标进行优化和校正。

在利用数学方法计算未知节点的位置坐标时，当选择的三个点在一条直线上时，就会导致形成的三个圆不能相交于一点，因此采用三边测量法就得不到正确的解。同时，三边测量法对测量出的估计误差非常敏感，而DV-Hop算法在估计平均跳距时会形成误差的累积，更加降低了节点的定位精度。而采用极大似然估计法可以将误差平均化，根据矩阵可以得到一个估计的解，但在估计平均每跳距离时会产生误差。从矩阵方程式AX=b来看，在方程式中引入了很多具有误差的已知量，因此极大似然估计法求解的节点误差还是很大的。那么，如果通过选择合适的适应值函数，利用量子粒子群算法对估算出的未知节点坐标进行优化，节点的定位误差一定会缩小，从而提高定位精度。

2 基于量子粒子群算法的DV-Hop定位算法

DV-Hop算法是基于非测距定位算法中最受关注的一个，但在利用跳数和平均跳距计算未知节点的未知坐标时存在一定的误差。为了减少节点定位过程中的误差，提高定位的精准度，有学者分别利用遗传算法[5]、模拟退火算法[6]、粒子群算法[7]对DV-Hop进行了优化。标准的粒子群算法在处理优化问题时要求的种群规模数量更多，在粒子迭代的后期搜索速度变慢，收敛的值容易陷入局部最优。因此，为了解决这些缺陷，文中采用量子粒子群算法对DV-Hop算法进行优化，对估计的节点坐标加以校正。量子粒子群算法能够以更小的种群规模进行搜索，在更短的时间内迭代得到最佳值，易实现且计算量小。

2.1 标准粒子群算法

粒子群算法[8]是模拟鸟群觅食行为，根据粒子的运动轨迹来进行全局搜索优化，具有易实现、搜索速度快、参数少和不需要梯度信息等优点，在科学研究和军事方面应用广泛。每个粒子都有一个相对应的适度值和速度矢量，分别表示距离及运动方向。在迭代算法中，通过比较每个粒子的全局极值Gbest和个体极值Pbest，然后对其位置和速度进行迭代更新[9]。

假设粒子种群数量为N，搜索空间的维度为D，则第i个粒子在D维空间中的位置表示为Xi=(xi1,xi2,…,xiD),i=1,2,…,N，该粒子的速度记为Vi=(vi1,vi2,…,viD),i=1,2,…,N。

通过每一次的迭代来寻找Pbest和Gbest，找到这个极值后再根据如下公式更新粒子的位置和速度：

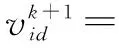
(1)

(2)

其中，pid和pgd(i=1,2,…,N，d=1,2,…,D)分别为粒子个体极值和全局极值的位置；k为迭代次数；c1，c2为学习因子；rand()为0到1之间的随机数；w为惯性权值[10]，通过合适的调节方法可以在局部寻优与全局寻优之间找到平衡。惯性权值越小，则局部寻优能力增强，全局寻优能力减弱；惯性权值越大，则全局寻优速度加快，局部寻优能力减弱。

2.2 量子行为的粒子群算法

粒子群算法在静态寻优方面具有良好的性能，但算法容易出现局部最优值和提前收敛的现象，其他外部因素也会影响算法的智能搜索能力。当前，研究者们主要是通过加入其他智能算法或使粒子发生变异以增加种群多样性等方式来处理这些缺陷。

粒子群算法在搜索过程中，有粒子的速度的概念，当算法早熟收敛到一个极值点时，所有的粒子容易聚集在一个固定的区域，它们的速度会变为零，这样一来粒子群就不再继续迭代搜索最优值，因此得到的解可能是局部最优值。为此，根据量子的概念，文中将量子行为融合到粒子群算法中。量子算法[11]在处理计算机问题时具有高效的计算能力，表明该算法在处理最优化问题方面有很好的优化搜索能力。

量子粒子群算法[12]是将量子计算的一些概念引入到粒子群算法中，使该算法更好地应用在优化搜索中[13]。但与经典的粒子群算法相比，两者有以下几点区别：

(1)描述粒子状态的信息不同。在量子空间中描述粒子状态的是一个波函数，而波函数是一个概率密度函数[14]，因此迭代变化中的粒子有不确定性的特点，该函数非常适合用来描述算法中寻优的粒子。

(2)取消了粒子群算法中的速度参数。粒子群系统是在量子系统模型下的，当然不需要存在经典力学中的速度概念。量子粒子群算法中的粒子不再受限于速度来更新迭代位置，而是在整个空间里进行全面优化搜索到最优解。

(3)没有“速度”参数，粒子更新迭代的方式也有所不同。经过前人的研究总结，假设粒子种群数量为N，搜索空间的维度为D，则第i个粒子在D维空间中粒子的进化方程为：

(3)

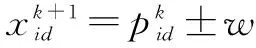
(4)

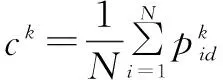
(5)

采用一种非线性策略来调整该系数w，从而改进量子粒子群算法。

(6)

其中，wmax和wmin分别为收缩-扩张系数的初始值和迭代结束值；kmax为最大迭代次数；k为当前迭代次数。

最后，当最优位置的适应度值符合最小适应阙值或者迭代次数等于最大值时，该QPSO算法结束。

2.3 QPSO算法的性能比较

为了验证改进算法的性能，利用2个经典函数(见表1)对标准PSO算法和改进的QPSO算法进行对比实验，根据实验结果分析改进算法的优越性和可行性。

表1 测试函数

图1和图2分别是QPSO和PSO算法的收敛曲线。

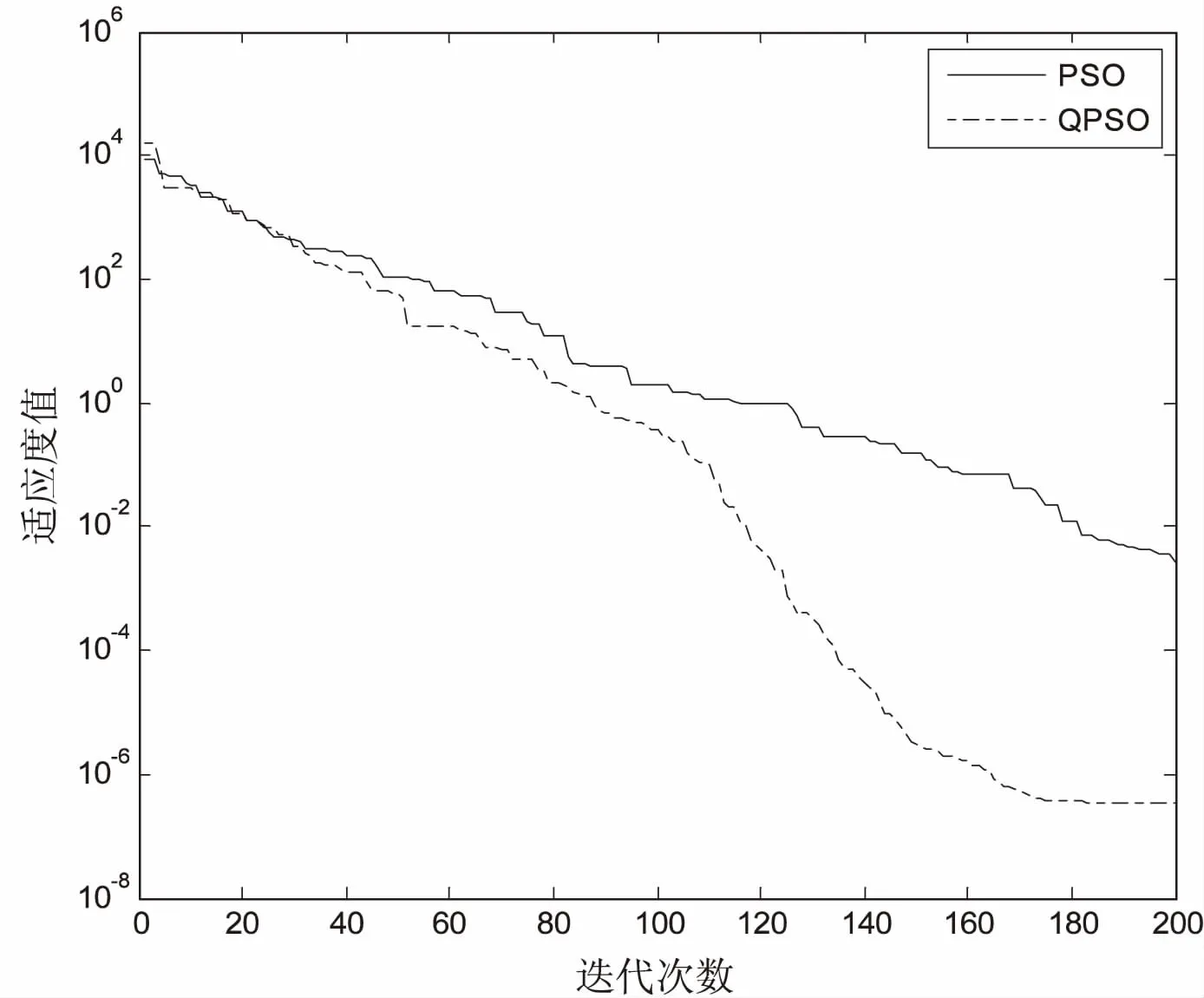
图1 测试函数f1(x)

图2 测试函数f2(x)

通过对比发现，QPSO算法不仅提高了精度，而且加快了寻优的求解速度和收敛速度。同时，QPSO算法的迭代次数明显少于PSO算法，适应值在更早的时候趋于稳定状态，减少了不必要的迭代。仿真结果表明，改进的QPSO算法在优化DV-Hop算法时，能在很大程度上减少计算量。

2.4 QPSO算法对DV-Hop算法优化的步骤

通过量子粒子群算法对DV-Hop算法进行优化，寻找未知节点到信标节点的实际距离与估计距离之间的最小误差，从而达到对未知节点位置的估计。文中算法流程如下：

Step1:在一定范围内随机产生若干传感器节点，通过DV-Hop算法的前两步，根据得到的跳数和平均跳距得到未知节点到信标节点的估计距离,然后用极大似然估计法计算出未知节点的坐标。

Step2：初始化网络。根据每个未知节点的估计结果在限定的范围内初始化种群，设定粒子个数及每个粒子大小并随机初始化各个粒子的位置，设置收缩扩张系数的初始值和结束值，最大迭代次数。

Step3：粒子空间位置的优劣只能由适应度函数衡量，函数决定着整个算法的优化效果。根据实际问题的要求，将跳数的倒数设计在函数中，采用的适应度函数为：

fitness(x,y)=

(7)

其中，fitness(x,y)为粒子i的适应度值；(xi,yi)为信标节点i的坐标值；(x,y)为粒子i的坐标值；di为未知节点到信标节点i的实际距离；θi与未知节点到信标节点i的跳数成反比。

Step4：评价种群中所有的粒子。根据设计的适应值函数，算法开始时计算每个粒子的适应值，然后把这些适应值分别设置为其粒子的最优值。通过比较每个粒子的最优值，得到一个全局的最优值，并记录该全局最优值所对应的粒子位置为全局最优位置。

Step5：通过式3～5更新粒子的位置状态，根据式6更新收缩扩张系数。

Step6：如果重新计算更新后粒子的适应度值优于以前位置的适应度值，则新位置取代以前位置成为下次迭代的起点，否则下一次迭代的起点不变。

Step7：若全局极值满足小于设定的阙值或者迭代次数达到最大的条件，则改进QPSO算法结束。否则，转至Step3，继续进行迭代运算。

Step8：将迭代结束得到的全局最优位置作为未知节点的估计位置。

3 仿真实验与分析

3.1 仿真环境与参数

为了验证量子粒子群算法的迭代优化性能，在MatlabR2010a平台上进行仿真实验。仿真过程中，传感器节点被随机分布在100 m×100 m的正方形目标区域内。算法的主要参数设置为：未知节点的个数为100，种群规模为20，最大迭代次数为100。为了减少实验中人为因素的干扰，节点定位误差取30次实验的平均值。采用标准化节点定位误差来评价算法性能，标准化节点定位误差为:

AverageError=

(8)

其中，(x,y)为未知节点的实际坐标；(xki,yki)为第K次估计未知节点i的坐标；R为节点的通信半径；N为未知节点的个数；K为实验次数。

3.2 不同节点数目的定位误差分析

通过调节节点总数，在保持锚节点密度不变的条件下，对比DV-Hop、PSO-DVHop和文中改进算法的定位性能。图3是节点从100增加到550的过程中各个算法的平均定位误差变化曲线。从图中可见，当节点总数逐渐增加时，三种算法的定位误差都有不同程度的下降，但改进算法误差下降幅度明显。三种算法的曲线都有一定的波动，这是由于每次仿真实验时，网络部署的节点都是随机生成的，因而误差上下有所浮动。

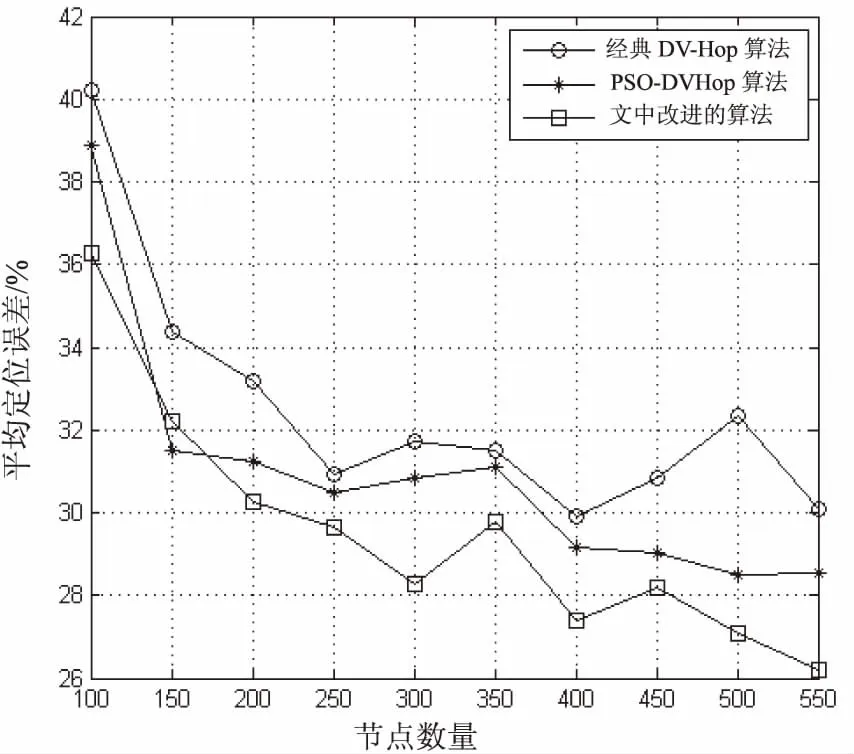
图3 节点数量-平均定位误差

3.3 不同锚节点密度的节点定位分析

通过调节锚节点密度，对比DV-Hop、PSO-DVHop和文中改进算法的定位性能。图4是锚节点密度从0.04变化到0.22的过程中各个算法的定位误差变化曲线。从中可见，当锚节点密度逐渐增大时，算法的平均定位误差在逐渐减小，但变化幅度在减缓。在相同的锚节点密度下，文中算法的定位精度更高。

图4 锚节点比例-平均定位误差

3.4 不同通信半径对节点定位误差的影响

在保持节点总数和锚节点密度不变的情况下，通过调节节点的通信半径大小，对比DV-Hop、PSO-DVHop和文中改进算法的定位性能。图5是通信半径从5变化到50的过程中各个算法的平均定位误差变化曲线。从中可见，当节点的通信半径在逐渐增加时，网络拓扑结构中的跳数会发生改变，节点之间的跳数相应减小，从而定位误差将会减小。文中改进算法能很好地降低定位误差。

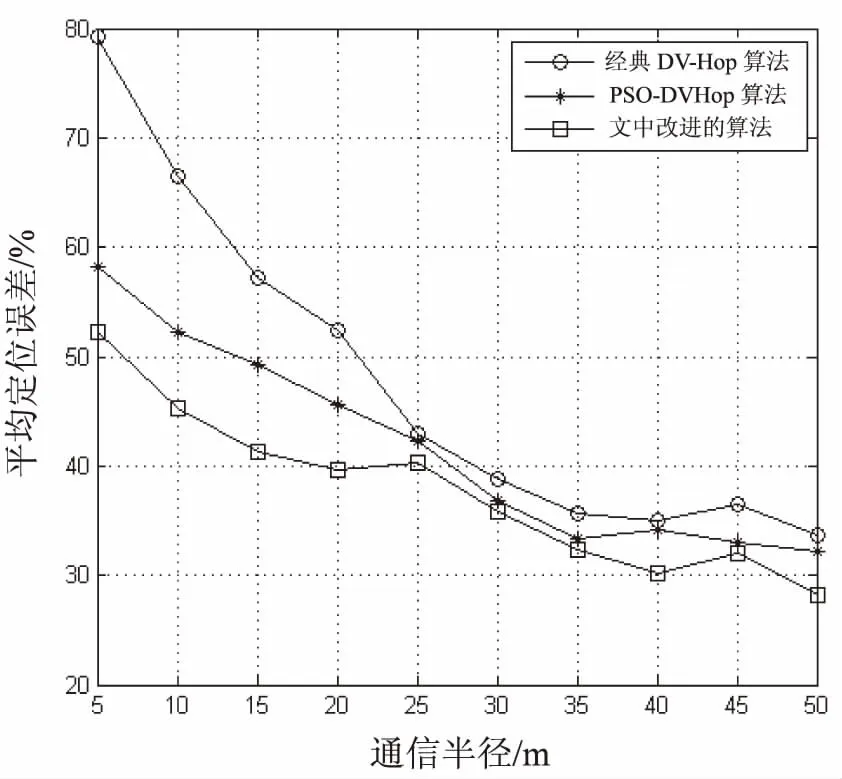
图5 通信半径-平均定位误差

4 结束语

为了提高传统DV-Hop定位算法的性能，提出用改进的量子粒子群算法来代替粒子群算法来优化节点定位。在保持节点定位硬件成本不变和一定的通信量范围内，定位节点的精确度更好，一定程度上解决了运用PSO来优化DV-Hop时的定位缺陷问题，体现了该算法的优越性。仿真结果表明，该算法虽然增加了一些计算量，但是节点的平均定位误差减少10%～15%左右，定位精度得到明显的提高。

参考文献:

[1] AKYILDIZ I F,SU W,SANKARASUBRAMANIAM Y,et al.Wireless sensor networks:a survey[J].Computer Networks,2002,38:393-422.

[2] NICULESCU D, NATH B. DV based positioning in Ad Hoc networks[J].Telecommunication Systems,2003,22(1-4):267-280．

[3] 王小平,罗 军,沈昌祥.三边测量法的结果稳定性研究[J].计算机工程与科学,2012,34(6):12-17.

[4] 徐原博,钟丽鸿,崔 洋,等.基于无线传感器网络的极大似然定位法的分析[J].传感器与微系统,2011,30(10):37-40.

[5] LI Wenwen,ZHOU Wunen.Genetic algorithm-base localization algorithm for wireless sensor networks[C]//2011 seventh international conference on natural computation.[s.l.]:[s.n.],2011:2096-2099.

[6] 吴意乐,何 庆.基于改进遗传模拟退火算法的WSN路径优化算法[J].计算机应用研究,2016,33(10):2959-2962.

[7] 陈星舟，廖明宏，林建华.基于粒子群优化的无线传感器网络节点定位改进[J].计算机应用,2010,30(7):1736-1738.

[8] 李凌燕,杜永贵.改进型粒子群优化在WSNs节点定位中的应用[J].计算机应用与软件,2014,31(4):69-72．

[9] 刘 逸.粒子群优化算法的改进及应用研究[D].西安：西安电子科技大学,2013.

[10] 林伟民,周宁宁.线性递减的粒子群优化算法[J].计算机技术与发展,2014,24(10):67-70.

[11] 张 毅,卢 凯,高颖慧.量子算法与量子衍生算法[J].计算机学报,2013,36(9):1835-1842.

[12] 潘大志,刘志斌.量子粒子群算法的改进实现[J].计算机工程与应用,2013,49(10):25-27.

[13] 王艳萍,张惠敏,刘新贵.基于量子粒子群优化算法的无线传感器网络节点优化[J].传感器与微系统,2010,29(2):32-34.

[14] 孙 俊,方 伟,吴小俊,等.量子行为粒子群优化:原理及其应用[M].北京:清华大学出版社,2011:30-39.

[15] 丁 颖,李 飞.自适应收扩系数的双中心协作QPSO算法[J].计算机工程,2014,40(3):232-237.