融合信息熵和加权相似度的协同过滤算法研究

李 玲，王移芝

(北京交通大学 计算机与信息技术学院，北京 100044)

0 引 言

为了缓解“信息超载(information overload)”造成的影响，推荐系统应运而生。推荐系统通过分析用户的行为，可以发现用户的潜在兴趣以及为用户提供个性化服务，例如Amazon的图书推荐[1]、YouTube的视频[2]等等。而协同过滤(collaborative filtering)是迄今为止应用最成功的个性化推荐技术[3]。协同过滤推荐的基本思想是根据用户之间的相似性预测用户的喜好，然后进行资源的推荐。因此，用户历史记录越多，协同过滤产生的推荐效果越好。然而，由于信息数量日益增加，用户对项目的评分数据也日益稀疏，推荐的精确度大幅降低[4-5]。

传统的协同过滤算法通常采用皮尔逊相关系数和余弦相似度度量用户之间的相似度。然而，传统的度量方法只考虑用户间共同评分项的信息，忽略了恶意信息的影响，对找到用户的近邻产生一定干扰。为降低数据稀疏性对系统推荐质量的影响，提高推荐精确度，针对上述问题，研究人员相继提出了多种应对办法。文献[6]提出使用sigmoid函数，提出SPCC方法强调共同评分项的重要性，评分项越多，用户间的相似度越大。另外，余弦相似度计算忽略用户的评分尺度，所以提出了改进的余弦相似度度量，即ACOS(adjusted cosine)[7]。文献[8]提出了一种结合项目时效性的算法，以缓解数据稀疏问题带来的影响，为用户推荐时效性高的项目。

尽管专家和学者们从不同角度提出了多种改进方法[9-10],并取得了理想的效果，但是用户关系的准确刻画仍然影响着推荐结果的精确度。因此，文中提出一种融合信息熵和加权相似度的协同过滤推荐算法。首先，根据用户-项目评分矩阵计算所有用户的信息熵，进一步计算用户的差异度信息熵值，再将用户的差异度信息熵融入到相似度计算中，最后使用新的相似度计算公式计算用户间的相似度，找到最合适的近邻，进行项目推荐。

1 传统的协同过滤算法

1.1 基于用户的协同过滤算法

传统的基于用户的协同过滤算法的步骤主要包括三部分[11]：用户-项目评分矩阵；发现最近邻居；产生推荐项目。

(1)用户-项目评分矩阵。

协同过滤推荐算法的研究基于用户的历史记录，这里用户对项目的评分数据用m×n的矩阵R表示。其中m表示用户的数量，其用户集合记为User={U1,U2,…,Ui,…,Um}，n表示项目数量,其项目集合记为Item={I1,I2,…,Ij,…,In},Rij表示用户i对项目j的评分，如表1所示。

表1 用户-项目评分矩阵

(2)发现最近邻居。

根据上述矩阵R，计算用户之间的相似度，将相似度按照降序的方式排列，前k个用户即为目标用户的最近k个邻居。

(3)产生推荐项目。

根据步骤2中找到的k个近邻对项目的评分情况，对目标用户没有过行为的项目按照公式1进行预测评分，然后将评分结果进行排序,将排名靠前的N个项目推荐给目标用户，即Top-N推荐。目标用户ut对项目j的预测评分公式如下：

(1)

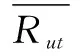
1.2 相似度计量方法

协同过滤算法的核心过程便是发现最近邻居，对计算用户之间的相似度起到了至关重要的作用。目前最常用的相似度计算方法有皮尔逊相关系数、余弦相似性和修正的余弦相似性[12]。具体如下：

(1)皮尔逊相关系数(Pearson correlation)。

sim(u,v)PCC=

(2)

(2)余弦相似度(cosine)。

(3)

(3)修正的余弦相似性(adjusted cosine)。

sim(u,v)ACO=

(4)

其中，C表示用户u和v共同评分的项目集合。

2 融合信息熵和加权相似度的协同过滤算法

2.1 信息熵

信息熵的概念是由香农(Claude Shannon)在1948年提出的，解决了信息的度量问题，主要通过随机变量取值的不确定性程度来刻画信息含量的多少[13]。

假设X是一个离散的随机变量，取值为{x1,x2,…,xn},记P(X=xi)=p(xi)，则可以用信息熵来表示X的不确定程度，其计算公式为：

(5)

由式1可以看出，信息熵的大小与X的概率分布有关，而与具体的取值无关。当p(x1)=p(x2)=…=p(xn)时，即对每一个用户来说，对项目评分出现的次数都是相等时，信息熵H(X)获得最大值。

文献[14-15]提出基于用户信息熵的协同过滤算法，首先计算用户的信息熵，低于信息熵阈值的用户信息属于噪声数据，然后过滤掉这些用户的信息以降低数据的稀疏性。但是存在的问题是用户的信息熵只与评分出现的次数有关，忽略了具体的评分值，这就导致有相同信息熵的用户可能会存在明显不同的评分倾向。例如，通过表2的计算可以发现，按照式5计算得到用户U1和U4的信息熵是相同的,容易划分为最近邻居范围。但是明显U1评分普遍偏高，U4评分普遍偏低，说明用户U1和U4可能不是最好的邻居。

表2 用户对项目的评分信息

针对上述问题，通过式6计算用户评分差异的信息熵值代替单纯的用户信息熵。假设用户U1和U2的共同评分项目集合为IC={I1,I2,…,In}，U1对共同项目的评分记为{U11,U12,…,U1n},U2对共同项目的评分记为{U21,U22,…,U2n}，则用户U1和U2的评分差集D12={|U11-U21|,|U12-U22|,…,|U1n-U2n|}={d1,d2,…,dn},然后计算H(D12)，即U1和U2的评分差异信息熵。这个值越小，表示二者之间的差异越小，评分越接近，选为最近邻居的可能性越大。

(6)

(7)

根据式7可知，信息差异熵的取值范围是[0,+∞)，因此需要对其进行归一化处理，使得H(Dij)的取值范围为[0,1],记为sim(u,v)WED。

2.2 加权相似度

考虑到不同用户的评分尺度和用户评分值对相似性的影响，增加度量用户相似性的信息量，同样可以降低数据稀疏性的影响。因此，采用加权相似度计算用户之间的相似性，在皮尔逊相关性的基础上引进权重因子α，取值在0～1之间，则新的相似度计算公式如下：

sim(u,v)NEW=α*sim(u,v)PCC+(1-α)*

sim(u,v)WED

(8)

从公式可以看出，通过权重因子α的调节，采用加权相似度计算用户的相似度，既提高了共同评分项目的重要性，也将用户的兴趣偏好考虑进去，从而提高了发现邻居的准确性。

2.3 算法步骤

根据以上描述，设计算法如下：

算法：融合信息熵和加权相似度的协同过滤算法

输入：用户-项目评分矩阵R,α

输出：MAE,RMSE

Step1:对用户-项目评分矩阵R,根据式5计算所有用户的信息熵Hi(1≤i≤m);

Step2根据式7计算多用户之间的差异信息熵H(Duv);

Step3:根据式8计算目标用户与参考用户的相似度，找到目标用户的最近邻居集合N;

Step4:根据式1，并参考最近邻居集合N，计算目标用户对未评分项目的预测评分值;

Step5:将预测评分值降序排列，产生推荐项目集;

Step6:根据推荐结果和式10、11，计算MAE的值。

3 实 验

3.1 数据集

应用于推荐系统研究的数据集包括公开的MovieLens,Netflix以及Jester等，不同数据集的稀疏度是不一样的。采用由明尼苏达大学GroupLens研究院小组提供的MovieLens_100K数据集，其评分尺度是从1到5的整数，数值越高，表明用户对该电影的偏爱程度越高，反之则表示用户对该电影不感兴趣。选用的数据集包括943个用户对1 682部电影的100 000条评分记录，每位用户至少对20部不同的电影进行过评分。该数据集的稀疏度为：

(9)

可见数据非常稀疏。数据集的内容共4列，分别是用户ID、电影ID、用户对电影的评分、时间戳。该数据集主要由两部分组成：base数据集和test数据集。其中base数据集作为样本数据集，经过训练后可以得到目标用户对未评分电影的预测评分；test数据集是用户对电影的实际评分，通过预测评分和实际评分的对比，可以得到推荐精度。

3.2 评价指标

推荐算法实验中常用的度量指标有均方根误差(RMSE)、平均绝对误差(MAE)、准确率、召回率等，文中采用MAE来度量，表示预测评分与实际评分之间的差距。计算公式如下：

(10)

(11)

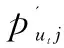
3.3 实验结果及分析

3.3.1 确定α的值

根据式8可知，参数α的值在相似度计算中起到了重要作用。为了获取最佳参数值，分别取参数的值为0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0,计算每个参数值相对应的MAE和RMSE，结果如图1和图2所示。图中四条折线分别表示近邻个数在取5，10，20，30时不同的结果。图1和图2表明，虽然近邻个数取不同的值，但是都在α=0.1时MAE和RMSE取得最小值，即当α=0.1时取得最佳推荐效果。

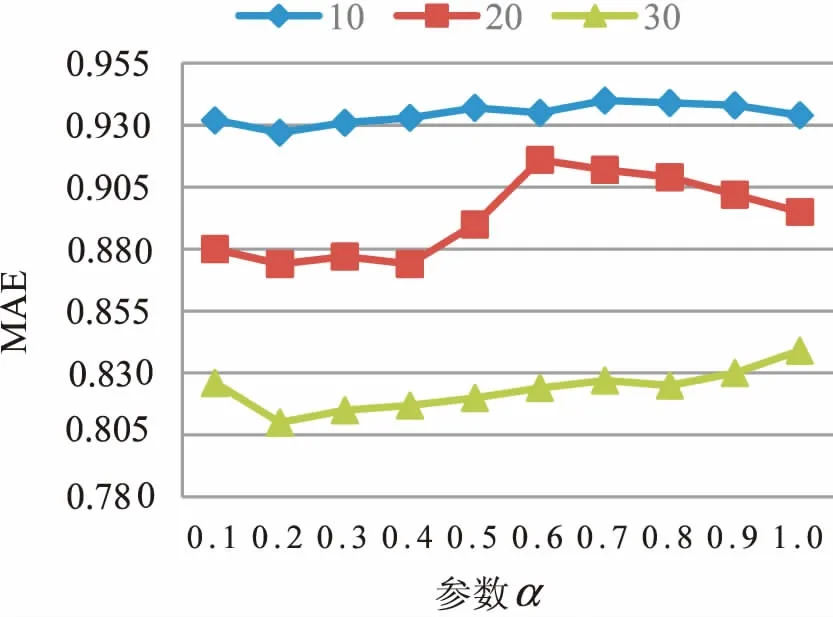
图1 不同α值对应的MAE

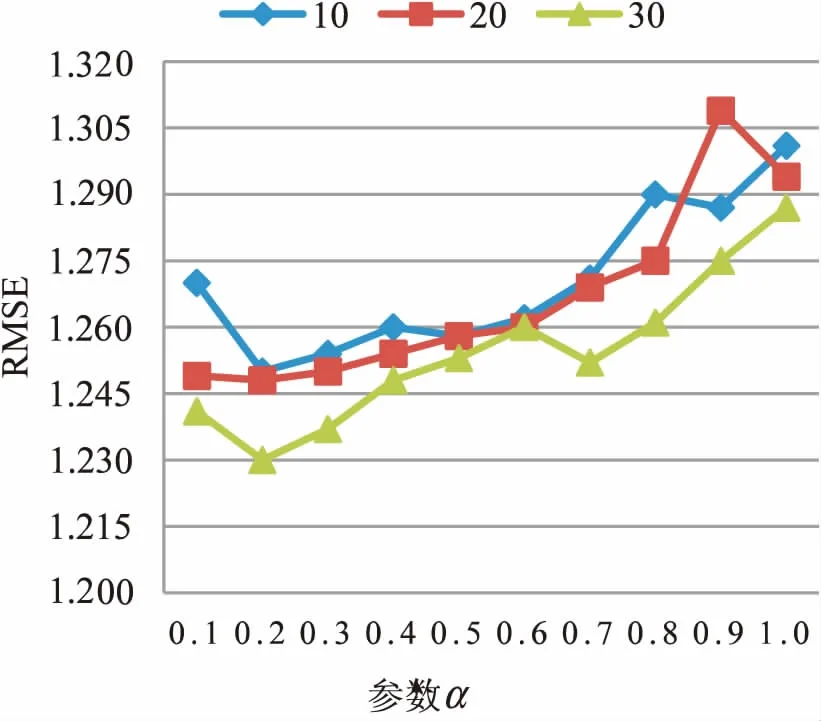
图2 不同α值对应的RMSE

3.3.2 实验结果与分析

根据以上所述，在使用加权后的相似度计算公式时，取α=0.1。接下来通过仿真实验，将传统的协同过滤算法(PCC)、使用信息差异熵作为相似度计算的协同过滤算法(WED)与提出的融合信息熵和加权相似度的协同过滤算法(NEW)进行对比，以验证该算法的有效性。图3和图4分别表示三种算法在不同近邻个数情况下的MAE值和RMSE值。

如图所示，不同的近邻个数也影响其MAE和RMSE的值。因为在适当的邻居范围内，推荐效果可以达到最佳，近邻个数太少，没有参考价值；相反近邻个数太多，会混入其他的噪声数据，因此选择适当的近邻个数也是必要的。

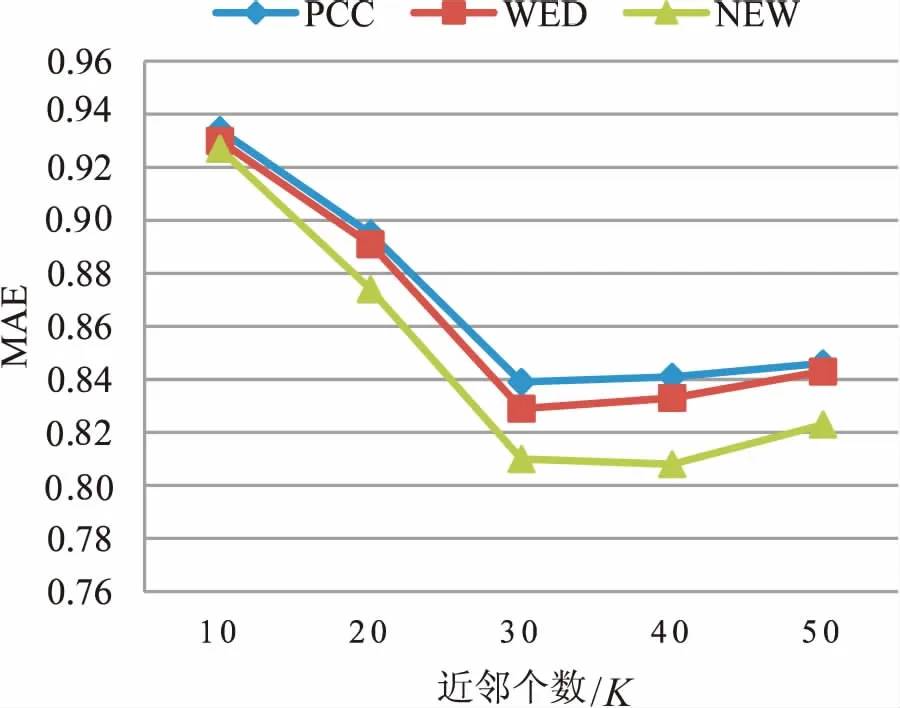
图3 三种算法对应的MAE值

图4 三种算法对应的RMSE值

另外，在近邻个数相同的情况下，提出的协同过滤算法相较于传统的协同过滤算法和基于信息差异熵的算法，其MAE和RMSE值均低于后两者，因此该算法可以有效提高推荐质量，缓解数据稀疏带来的问题。

4 结束语

在传统基于用户的协同过滤算法的基础上，通过引入用户间的差异信息熵值，可以在一定程度上有效缓解数据的稀疏性带来的影响。在此基础上，通过使用加权相似度的方式强化共同评分用户的作用，提高最近邻居的识别度。实验结果证明，融合信息熵和加权相似度的协同过滤算法有效提高了推荐效果。在提高推荐效果的基础上，进一步降低时间复杂度、缩短计算时间将是下一步的研究方向。

参考文献：

[1] 张宁昳.Amazon个性化推荐系统的文本组织结构研究[J].图书与情报,2013(5):103-106.

[2] BALUJA S,SETH R,SIVAKUMAR D,et al.Video suggestion and discovery for Youtube:taking random walks through the view graph[C]//Proceedings of the 17th international conference on world wide web.[s.l.]:[s.n.],2008:895-904.

[3] 邢春晓,高凤荣，战思南，等. 适应用户兴趣变化的协同过

滤推荐算法[J].计算机研究与发展,2007,44(2):296-301.

[4] SYMEONIDIS P,NANOPOULOS A,PAPADOPOULOS A,et al.Collaborative filtering based on user trends[M]//Studies in classification data analysis & knowledge organization.Berlin:Springer,2008:375-382.

[5] BOBADILLA J,ORTEGA F,HEMANDO A,et al.Recommender systems survey[J].Knowledge-Based Systems,2013,46:109-132.

[6] JAMALI M,ESTER M.Trustwalker:a random walk model for combining trust-based and item-based recommendation[C]//Proceedings of the 15th ACM SIGKDD international conference on knowledge discovery and data mining.New York,NY,USA:ACM,2009:397-406.

[7] SARWAR B,KARPIS G, KONSTAN J,et al. Item-based collaborative filtering recommendation[C]//Proceedings of the 10th international conference on world wide web.[s.l.]:[s.n.],2001:285-295.

[8] 刘江东,梁 刚,杨 进.基于时效性的冷启动解决算法[J].现代计算机,2016(5):3-6.

[9] 黄创光,印 鉴,汪 静,等.不确定近邻的协同过滤推荐算法[J].计算机学报,2010,33(8):1369-1377.

[10] 李 聪,梁昌勇,马 丽.基于领域最近邻的协同过滤推荐算法[J].计算机研究与发展,2008,45(9):1532-1538.

[11] 刘芳先,宋顺林.改进的协同过滤推荐算法[J].计算机工程与应用,2011,47(8):72-75.

[12] MULLER K R,MIKA S,RTSCH G,et al.An introduction to kernel-based learning algorithms[J].IEEE Transactions on Neural Network,2001,12(2):181-201.

[13] SHANNON C E A.A mathematical theory of communication[J].ACM SIGM-OBILE Mobile Computing & Communications Review,2001,5(1):3-55.

[14] 刘江冬,梁 刚,冯 程,等.基于信息熵和时效性的协同过滤推荐[J].计算机应用,2016,36(9):2531-2534.

[15] KALELI C.An entropy-based neighbor selection approach for collaborative filtering[J].Knowledge-Based Systems,2014,56:273-280.