基于小波包和改进EMD的脑电信号消噪研究

郑佳佳，郭滨

（长春理工大学 电子信息工程学院，长春 130021）

把大脑皮层或头皮表面的微弱的生物电通过脑电图描记仪画成曲线图，这个曲线图反映了脑电的活动情况，也叫做脑电图［1］（electroencephalogram，EEG）。脑电检测是遵照国际10-20电极放置系统，把脑电测试仪放于头部表皮上来察看大脑活动情况［2］的检测方法。

由于各种干扰信号会影响脑电信号的采集，包括眼电、心电、工频干扰等，为了更好的通过脑电信号来分析病情，在临床医学诊断中，给采集到的脑电信号进行去噪是必不可少的。脑电信号去噪处理方法有时域方法中的W-igner分布、小波包分析、小波分析、HHT分析，以及独立分量分析等。生物医学领域常用具有多分辨的小波变换，并且时频局部化特性较好，但其存在频率分辨率较差的高频段和时间分辨率较差的低频段等不足，在小波分解过程中，为了解决以上的问题，本文应用了小波包分析。

黄锷提出一种自适应时频分析的方法［3-5］。该方法又称希尔伯特-黄变换，它的重要环节是经验模态分解，自适应地分解了信号中的局部变化特征，然而，如果极值点不均匀的出现在信号中，分解结果图中会出现一个IMF分量上的多尺度信号，这就是模态混叠现象。这样分解得到的信号就不是所需要的，不利于接下来的研究。故使用可以有效抑制模态混叠现象的聚合经验模态分解（EEMD），之后对含噪声的IMF进行Hilbert变换，剖析Hilbert谱。将含噪的IMF分量进行小波包分析，最后叠加各分量，得到去噪后脑电信号。

1 基于EEMD算法的HHT方法

白噪声具有零均值，且频率谱均匀分布的特征，如果把脑电加入到不同的白噪声背景上，最后对结果求取总体均值，就可以消除噪声，这就是EEMD的改进部分。

EEMD算法步骤如下：

（1）给目标信号S(t)加入一组高斯白噪声n1(t)，获得一个总体S1(t)；

（2）对S1(t)进行EMD分解，得到n个imf分量，即：

（3）重复前二个步骤，每一次都加入新的白噪声；

（4）得到各自的imf分量组；

（5）将相应的imf总体均值作为结果：

其中，imfi(t)为第i个imf分量的总体均值；T为总的平均数；imfij(t)是白噪声加入第j次后得到的imf；

（6）将相应的剩余R的总体均值作为结果：

EEMD算法流程如图1所示。

图1EEMD算法

2 小波包分析

小波分析是基于正交小波基函数，将信号先处理成频率较高和频率较低的两部分，之后仅对频率低的进一步分解，不再分析频率高的，所以小波变换不能分解和表示高频段含有有用信息的信号，如生物医学信号等。而小波包分析不仅对低频段分解，而且还分析高频段，因此可以对中高频段含有的用信息的信号进行时频局部分析。小波包是小波分析基础结合最优基选择的结果。根据各个被分解的频带段信号特征，自适应的选择最优基函数去匹配信号，这样信号的分析就能提高，因此，小波包分析被广泛的应用到该领域中［6，7］。

2.1 小波包分解

在小波多分辨分析理论的基础上，将尺度函数φ(t)记为u0(t)，小波函数φ(t)记为u1(t)，则二尺度方程：

式中，u0(t)=φ(t)所对应的小波包为{un(t)}n∈Z，而H(k)，G(k)是共轭滤波器系数［8］。

假设S(t)是时间信号，pij(t)表示第j层上的第i个小波包，则二进小波包分解为：

2.2 小波包重构

式中，j=J-1,J-2,...,1,0;i=2j,2j-1,...,2,1;J=logN2，H是与尺度函数相关的一个小波包重构滤波器，G为与小波函数相关的另一个小波包重构滤波器。

小波包过程如图2所示。

图2 小波包分解过程

经过小波包分解后，S代表每一层被分解的高频和低频部分，其良好的时频分辨率正适合非平稳信号EEG的频域分析［9］。

3 消噪过程

带有噪声的脑电信号模型：

其中，S(t)是带噪信号；f(t)为纯净脑电信号；e(t)为噪声；ε为噪声强度。

基于改进的EMD结合小波包去噪的主要内容为：含噪的信号经过EEMD分解得到从高频到低频率的IMF分量，经观察可得噪声主要分布在高频部分，同时经过Hilbert谱分析，可以确定高频段含有噪声（前三个IMF分量中），不处理第4个到第9个的IMF分量，只需要通过小波包对含噪声的高频段IMF进行去噪处理，最后把新的前三个IMF分量和后面的6个原始分量相加，即为处理过噪声的脑电信号。

具体步骤如下所示：

（1）对带噪脑电信号S(t)进行EEMD分解，得到n个IMF分量；

（2）计算每个IMF分量的Hilbert谱：

（3）通过小波包分析对前三个IMF分量进行处理；

（4）把留下来的低频部分IMF与经过小波包处理的高频部分IMF相加起来，可以得到去过噪声的脑电信号；

（5）用均方根误差（RMSE）和信噪比（SNR）来说明消噪效果，表达式如下：

其中，xi为i时刻在原始信号上的采样值；xi是去除噪声后的值；N是信号序列长度。信噪比SNR反映了去除噪声的信号中噪声所占的比值，SNR和均方根误差RMSE是呈反相关系的，研究需要信噪比大的，信号的去噪效果就更好。

4 实验结果与分析

实验数据来源于身体健康的在校研究生，在放松闭眼状态下，1000赫兹为采样的频率，采样的时间是3秒。实验中有噪声的脑电信号与加入的白噪声标准差之比为5，总体的平均次数是100。脑电信号在F3通道里获取，然后进行EEMD分解，最终得到9个IMF分量和一个剩余量R，所得IFM分量的时域图如图3、4所示。由图可知，不同的时间特征尺度对应各阶IMF分量，并且随着阶次的增长，频率从高频到低频出现。

图3EEMD分解后IMF分量时域图

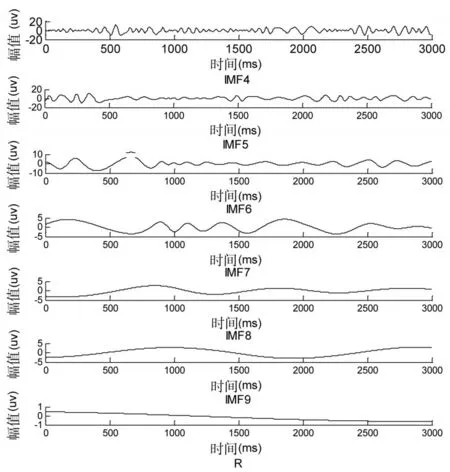
图4EEMD分解后IMF分量时域图

由于脑电信号主要集中在0-30HZ，而高频部分主要分布在前3层的IMF分量中，所以噪声主要存在于这三层，然后进行前3个IMF分量的Hilbert谱分析可以得出这3层含有噪声（如图5），因为点分布比较分散，有少量的能量。因此，只对这三层IMF分量进行改善，利用小波包去噪处理。消噪效果如图6所示。

图5 Hilbert谱

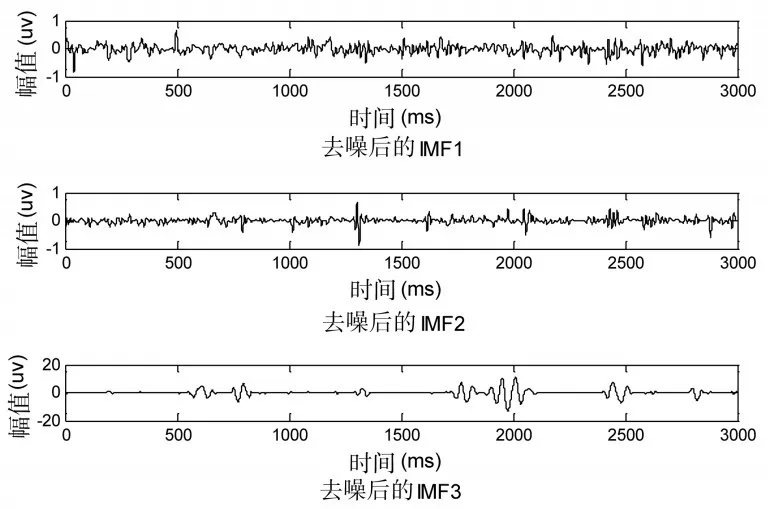
图6 小波包去噪后的IMF1，IMF2，IMF3

最后，把通过小波包去噪后的IMF1～IMF3和其他保留的IMF分量进行叠加，可以得到改进EMD结合小波包去噪后的脑电图，和小波包消噪、改进EMD去噪相对比，三种方法的消噪结果如图8、9、10所示。

图7 原始信号

图8 小波包去噪

图9 改进EMD去噪

图10 改进EMD结合小波包去噪

三种去噪方法的2个评价指标如表1所示。

表1 3种消噪方法评价指标比较

由表1可知，改进EMD结合小波包方法比单独使用小波包方法具有更高的信噪比和更低的均方根误差，故消噪效果更佳。这是因为本文使用的方法不仅可以抑制模态混叠现象，而且可以得到更多高频部分的有用信息。

5 结语

本文把改进EMD的HHT方法结合小波包来进行脑电信号的去噪。运用EEMD在EEG信号中加入白噪声，接着对高频部分对应的IMF分量进行HHT谱分析，可以得到含噪声的高频分量，最后对其进行小波包去噪处理，可以更大限度的得到有用信息，有效的消除噪声。经验证，改进EMD结合小波包去噪效果更好。有利于未来推动临床医学方法的研究及一些疾病的诊断与预防。

参考文献

［1］ 王兆源，周龙旗.脑电信号的分析方法［J］.第一军医大学学报，2000，20（2）：189-190.

［2］ 季忠，秦树人，彭丽玲.脑电信号的现代分析方法［J］.重庆大学学报，2002，25（9）：108-112.

［3］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.J Proc Rsoc Londna，1998，454（1971）：903-995.

［4］ 韩立喜.心音信号去噪及特征值提取的研究［D］.长春：长春理工大学，2013.

［5］ 黄友朋，赵山，许凡，方彦军.EEMD排列熵与PCA-GK的滚动轴承聚类故障诊断［J］.河南科技大学学报：自然科学版，2017，38（02）：17-24，30.

［6］ Yang BH，Yan GZ，Yan RG，et al.Adaptive subject-based feature extraction in brain-computer interfaces using wavelet packet best basis decomposition［J］.Medical Engineering&Physics，2007，29（1）：48-53.

［7］ Mcfarland DJ，Anderson CW，Muller KR，et al.BCI meeting 2005-workshop on BCI signal processing：feature extraction and translation［J］.IEEE Trans.Neural Syst.Rehabil.Eng.，2006，14（2）：135-138.

［8］ 张国华，袁中凡，李彬彬.心音信号特征提取小波包算法研究［J］.振动与冲击，2008，27（7）：47-49.

［9］ 杨帮华，陆文宇，何美燕，等.脑机接口中基于WPD和CSP 的特征提取［J］.仪器仪表学报，2012，33（11）：2560-2565.