基于训练序列的UFMC符号定时同步改进算法

余翔，周志义，段思睿，陈和力

（重庆邮电大学，重庆 400065）

1 引言

随着4G进入规模商用，5G移动通信的研究工作已经全面开启[1]。在4G系统中，OFDM技术凭借频谱效率、对抗多径衰落、低实现复杂度等方面的优势，被广泛应用于各类无线通信系统。但是OFDM技术存在较高的峰值平均比、对频率偏移敏感、受保护间隔影响、适配各种业务灵活性不够[2]等缺点，使其不能很好地满足5G中更加多样化、更高的频谱利用率、更加海量的连接等需求[3]。为了克服OFDM技术的缺点，并更好地支持5G中连续广域覆盖、热点高容量、低功耗大连接、低时延高可靠四大应用场景[4]，多种新型多载波技术被提出。通用滤波多载波[5]（universal filtered multi-carrier，UFMC）技术是新型多载波技术中的典型代表之一，凭借其良好的带外抑制、不需要 CP、极高的频谱利用率、载波间的宽松同步、合理利用碎片频谱等优点，成为5G候选波形中极具竞争力的技术[6]。

对于多载波通信系统而言，在接收端定时偏差的大小会直接影响到最终的还原数据的误码率。因此符号同步技术是一项必不可少的关键技术。对于UFMC系统而言，定时偏差会造成相应的干扰，诸如 ISI、ICI、IBI[7,8]。因此，较大的定时偏差会导致UFMC系统的性能下降。为了确保UFMC系统的高性能，必须很好地解决符号定时同步的问题。目前，对于符号定时同步技术的研究比较成熟，但是大部分的研究成果都是关于OFDM和FBMC系统的，而关于UFMC系统的符号定时同步技术则相对较少。Schmidl等人[9]提出的S&C算法是针对OFDM系统的一种经典的符号定时同步算法，将该算法引用到 UFMC系统中时，因为UFMC系统采用的滤波器，定时测度函数曲线会产生平台效应，而又因为UFMC系统没有采用CP，该平台对定时估计影响很大，会降低定时估计的精确度。Wang等人[10]根据S&C算法的思想，利用两个相同的训练符号构成重复的训练序列结构，然后进行相关性检测对起始位置进行定时估计。该算法虽然具有较高的精确度，但是两个符号的使用增加了同步的开销。Cho等人[11]针对 UFMC系统提出一种粗符号定时同步算法，该算法通过构建具有重复数据部分的训练符号，结合完全相同的数据部分和具有较强相关性的数据部分，进行相关性检测，最终取最大的相关性位置为最佳定时估计时刻。因为利用了滤波器影响的数据部分的相关性减小了平台的长度，仍然存在较短的平台，因此算法精确度提升较低。

为了解决因采用滤波器导致符号定时同步算法在UFMC系统中的精确度偏低的问题，本文提出了一种基于训练序列的改进算法，该算法通过对训练符号进行重新设计，消除了滤波器对定时估计的负面影响，定时测度函数曲线得到一个尖峰，提高了定时估计的精确度，体现了本文提出的改进算法的有效性。

2 UFMC系统模型

UFMC系统模型[12]如图1所示，将总带宽划分为B个子带，每个子带分配ni个连续子载波，并且每个子带对应于LTE中的物理资源块，总共有个子载波。频域信号Xi经过N点的离散傅里叶逆变换（IDFT）成时域信号xi，其数学表达式为：

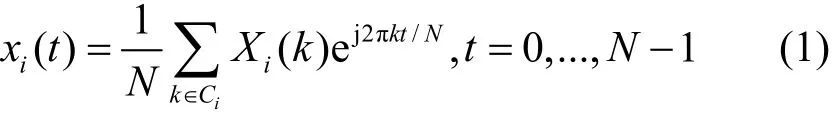
其中，N表示IDFT点数；i表示UFMC子带的序号；Ci表示第i子带中所有子载波的集合；k表示Ci中的第k个子载波；t表示时间索引。

然后输出时域信号xi用长度为L的FIR滤波器fi进行滤波，时域信号xi与滤波器fi进行线性卷积运算，得到长度为的信号Si。最后将所有子带信号Si进行叠加，生成UFMC符号，数学表达式为：

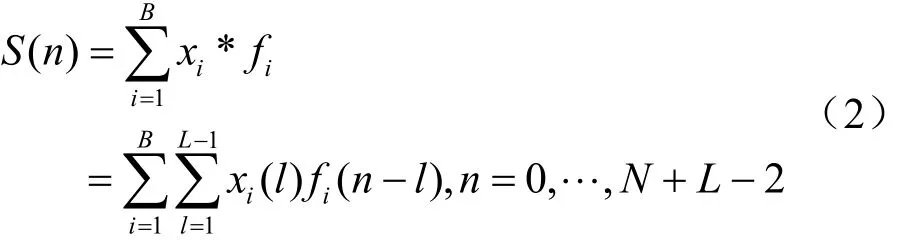
其中，“∗”表示线性卷积计算；fi表示子带i对应滤波器的冲激响应函数，并且满足L表示切比雪夫滤波器长度。

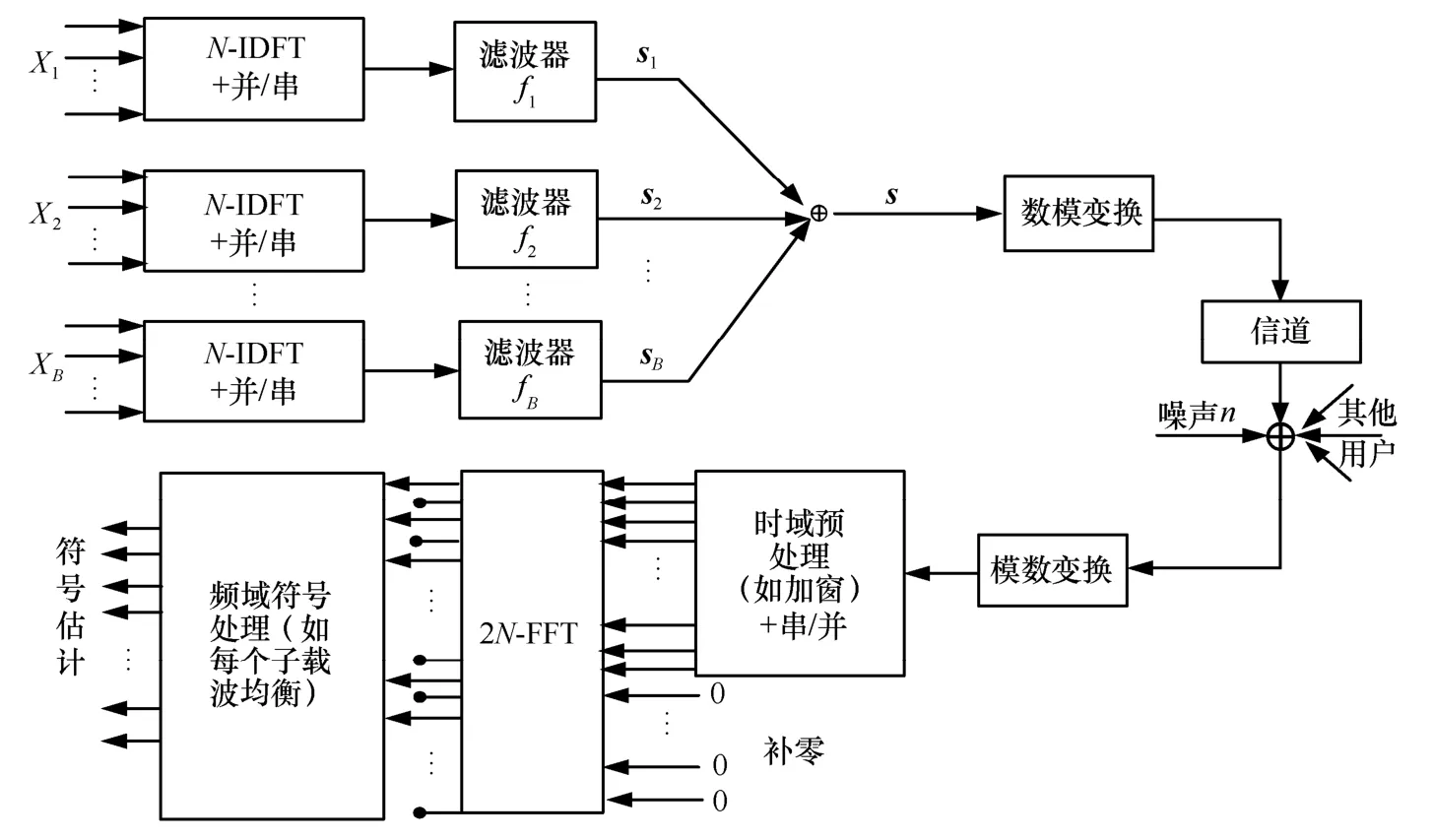
图1 UFMC系统模型

3 UFMC符号定时同步算法

3.1 基于S&C算法

Schmidl&Cox针对OFDM系统提出的S&C算法是用来解决符号定时同步问题的经典算法，该算法根据OFDM符号的特性生成前后两部分数据重复的训练符号，算法通过对接收的信号进行相关性检测来完成定时估计。将该算法引用到UFMC系统中，在偶载波上插入数据，在奇载波上插0，就可得到具有重复数据部分的训练符号。用于符号定时估计的训练符号的结构如图2所示。

图2 基于S&C算法训练符号结构

图2中的训练符号结构只用到了符号中的重复部分数据，因此该训练序列结构中用于定时同步的数据结构可以表示为：

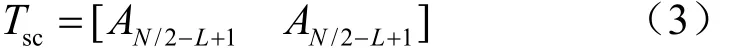
式（3）中，N表示IDFT点数；L表示滤波器长度；表示数据部分A的长度，其持续区间为[L,N/2-1]。

定时度量函数为：

其中：

式（5）中，r(d)为接收信号，r*(d)为接收信号的共轭，Psc(d)为d时刻的相关函数，式（6）中，为d时刻能量函数。

F·雷卡尼出生于1985年，毕业于德黑兰大学艺术学院，是伊朗“80后”新生代漫画家的代表人物之一，也是伊朗为数极少的职业漫画家之一。同时他的油画也颇具实力，意大利、瑞士、土耳其和德国都有画廊代理其作品。雷卡尼的漫画常常采用较为写实而有力的钢笔线条，加之以局部着色，一眼效应非常突出。除在伊朗的各大报刊刊登他的漫画作品之外，他还在欧洲和叙利亚、约旦等多国报刊开设时事和幽默漫画专栏，广受各国媒体业界人士青睐。雷卡尼分别于去年和今年应邀在意大利和土耳其举办了个人艺术展，其中包括他的单幅以及连环漫画。（选自人民网http://www.people.com.cn/）

最佳定时估计位置判定规则：先找到测度值的最大值，然后设定阈值threshold=0.9并选取处的两个时刻d1和d2，则最佳的定时估计值为：

UFMC系统由于采用滤波器，影响了符号的特性，导致在一定范围内定时测度函数会产生平台效应，从而使得定时估计的精确度偏低。

3.2 Cho算法

Cho等人[11]提出了一种针对UFMC系统的粗符号定时同步算法，本文将该算法简称为Cho算法，该算法训练符号的生成过程与基于S&C算法相似，在奇数子载波上插入 0，不同之处是 Cho算法用 ZC序列插入偶数子载波上。生成一个中间两部分数据具有较高相关性的训练符号，该算法的训练序列结构如图3所示。

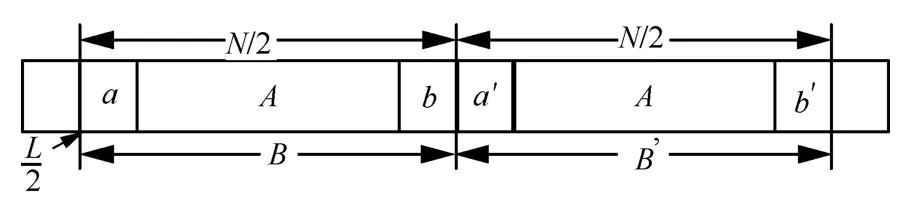
图3 Cho算法训练符号结构

图3中的Cho算法除了利用训练符号结构中[AA]数据部分具有强相关性外，还利用了[aa']和[bb']数据部分因为滤波过程而具有较高的相关性，因此Cho算法的训练符号结构中用于定时同步的数据结构表示为：

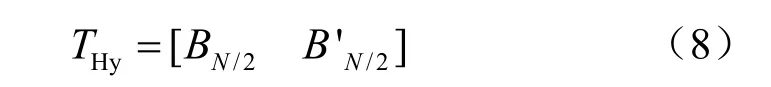
具体算法如下：

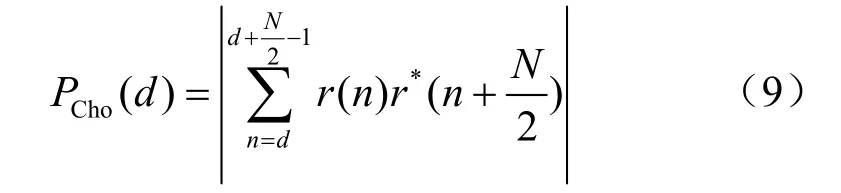
Cho算法通过式（9）进行相关性检测，根据PCho最大值的位置可以得到最佳定时估计值。以上为参考文献[11]中提出的 Cho算法，本文为了方便与其他算法进行对比，对该算法进行能量归一化处理：

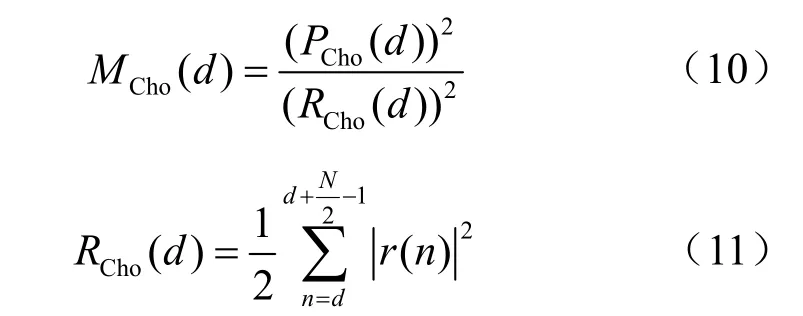
最佳定时估计值更改为取定时测度函数MCho(d)的最大值的位置。Cho算法是在S&C算法的基础上加入了由于滤波过程而产生较高相关性的[aa']和[bb']数据部分的相关性，但也因这两部分数据只是具有较高相关性而不是完全相同的，Cho算法也会产生一个平台，但是Cho算法的平台要比基于 S&C算法的平台的长度小，因此Cho算法的精确度要比基于S&C算法高。

3.3 改进算法

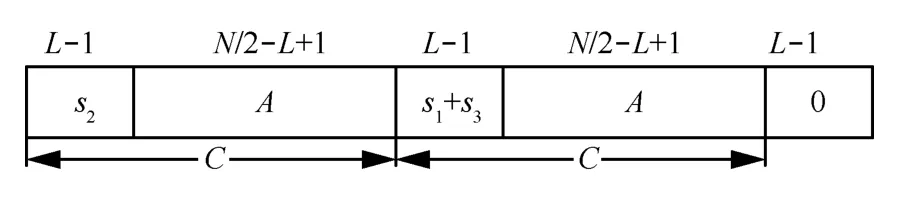
图4 改进算法训练符号结构

图4中为本文提出的新的训练符号结构，其中包含了两部分相同数据部分以及全零数据部分，新的训练序列结构中用于定时同步的数据结构可以表示为：

改进算法是利用前面两部分相同数据的相关性，进行相关性检测，改进算法的定时测度函数如下：

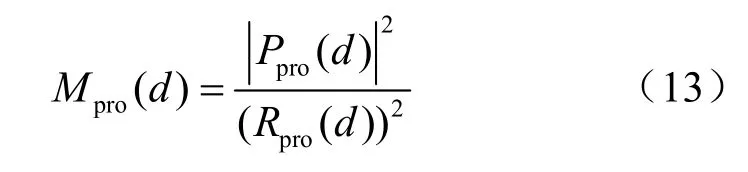
其中：

式（14）、式（15）中的d表示时间刻度，k表示时间偏移量。最佳定时估计位置为Mpro(d)取最大值时对应的位置，可以表示为：

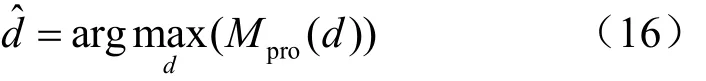
本文提出的改进算法对训练符号进行重新设计，新训练符号利用UFMC符号首尾数据相加等于中间数据的特性，经过相应的操作生成具有重复部分的训练符号。该训练符号重构了滤波器影响的数据片段，实现了消除平台效应的效果，并使得改进算法的定时测度函数曲线峰更加尖锐，最终可以提高定时估计的精确度、优化定时同步的性能。

4 仿真结果与分析

本节将利用 MATLAB对符号定时同步算法进行蒙特卡洛仿真，分析本文提出改进算法的性能。本文仿真参数见表1。

表1 仿真基本参数

在信噪比为30 dB的AWGN信道条件下，基于S&C算法、Cho算法和本文提出改进算法的定时度量函数的仿真曲线如图5所示。从图5中可知，基于S&C算法和Cho算法由于滤波器的影响，定时测度函数出现了一个平台效应，造成精确度偏低。同时Cho算法的平台要比基于S&C算法的短，故Cho算法的精确度要比基于S&C算法高一点。然而本文改进算法因为对训练符号进行了重新设计，消除了滤波器对定时测度函数曲线的影响，间接地消除了平台效应。其函数曲线出现了一个尖峰，有利于定时位置的判定，提高了算法的精确度。

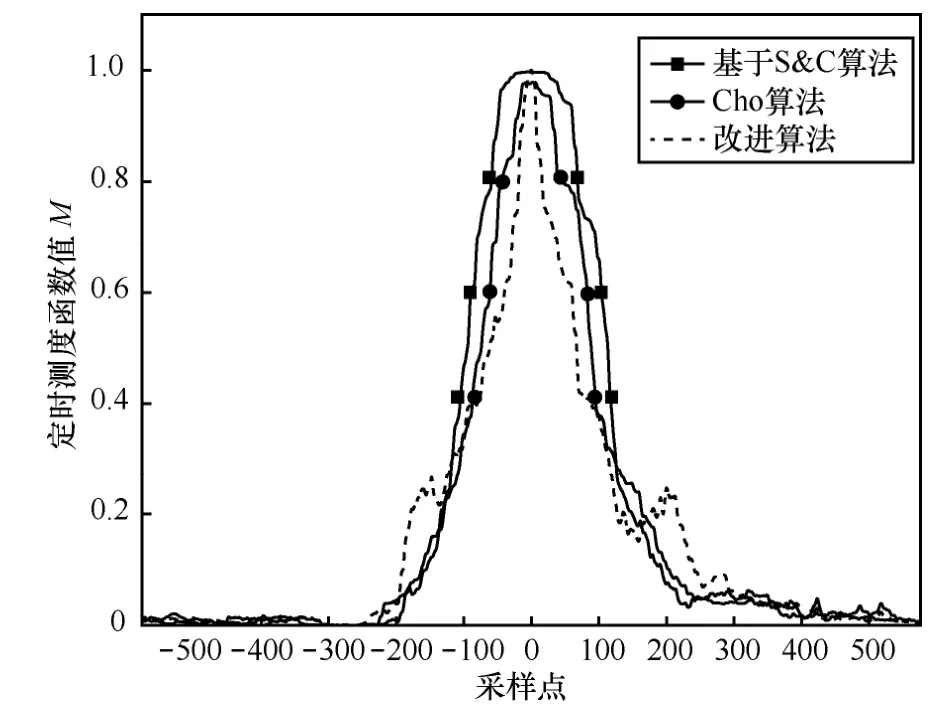
图5 3种算法的定时度量函数曲线

图6中仿真了3种算法在不同信噪比下，定时估计值的均方根误差。从图6中可以看出，基于S&C算法和Cho算法随着信噪比增大而不断减小，且当SNR＞15 dB时，减小趋势趋于平稳，不再减小。而本文提出的改进算法则是随信噪比的增大不断减小。另外，基于S&C算法由于较长平台的存在，均方根误差比较大，而Cho算法的平台长度较小，其均方根误差会比基于S&C算法的小。最后本文提出的改进算法因为测度函数在定时估计时刻有一个尖峰，所以均方根误差比其他两种算法的都要小。

5 结束语

UFMC系统由于采用滤波器，基于S&C符号定时算法会产生较长平台，最终导致定时估计值的精确度偏小。而Cho算法的改进只是缩短了平台的长度，在一定程度上较基于S&C算法提高了定时估计的精确度，但精确度比较低。为此，借鉴Cho算法利用滤波过程影响的数据部分的特性的思想，本文利用滤波处理过程造成符号的首尾数据部分相加等于中间数据的特性，对训练符号进行重新设计。改进算法的定时测度函数能够得到一个尖峰，便于定时估计。从仿真结果可以看出，本文提出的改进算法定时估计的精确度更高，性能更好。后续研究可以利用因滤波处理而产生的特殊性质重新设计一个特殊的训练符号，从而实现算法性能的提升。

图6 不同信噪比下3种算法的定时估计均方根误差

参考文献：

[1]陈晓贝, 魏克军.全球5G研究动态和标准进展[J].电信科学,2015, 31(5)： 16-19.CHEN X B, WEI K J.Global research and standardization progress of 5G[J].Telecommunications Science, 2015, 31(5)： 16-19.

[2]谢显中.第 5代移动通信基本要求与新型多址复用技术[J].重庆邮电大学学报(自然科学版), 2015, 27(4)： 434-440.XIE X Z.Key requirements and multi-access multiplexing techniques for 5G[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2015, 27(4)：434-440.

[3]IMT-2020 (5G) 推进组.5G概念白皮书[R].2015.IMT-2020 (5G) Advance Group.5G concept white paper [R].2015.

[4]王胡成, 徐晖, 程志密, 等.5G 网络技术研究现状和发展趋势[J].电信科学,2 015, 31(9)： 156-162.WANG H C, XU H, CHENG Z M, et al.Current research and development trend of 5G network technologies[J].Telecommunications Science, 2015, 31(9)： 156-162.

[5]VAKILIAN V, WILD T, SCHAICH F, et al.Universal filtered multi-carrier technique for wireless systems beyond LTE[C]//2013 IEEE GlobeCom Workshops, June 5, 2014, Atlanta, GA, USA.Piscataway： IEEE Press, 2013： 223-228.

[6]杨路, 何萍, 王珊.UFMC系统中的载波频率同步技术[J].电信科学, 2016, 32(11)： 50-55.YANG L, HE P, WANG S.Carrier frequency synchronization technology in UFMC[J].Telecommunications Science, 2016,32(11)： 50-55.

[7]WANG X, WLID T, SCHAICH F.Universal filtered multi-carrier with leakage-based filter optimization[C]//2014 IEEE European Wireless Conference, June 27, 2014, Barcelona, Spain.Piscataway： IEEE Press, 2014： 1-5.

[8]WANG X, WLID T, SCHAICH F.Filter optimization for carrier-frequency and timing-offset in universal filtered multi-carrier systems[C]//2014 IEEE Vehicular Technology Conference, July 2, 2015, Glasgow, UK.Piscataway： IEEE Press, 2015： 1-6．

[9]SCHMIDL T M, COX D C.Robust frequency and timing synchronization for OFDM[J].IEEE Transactions on Communications, 1997, 45(12)： 1613-1621.

[10]WANG X J, SCHAICH F, BRINK S.Channel estimation and equalization for 5G wireless communication systems[D].Stuttgart： University of Stuttgart, 2014.

[11]CHO H, YAN Y, CHANG G K, et al.Asynchronous multi-user uplink transmissions for 5G with UFMC waveform[C]//2017 IEEE Wireless Communications and Networking Conference(WCNC), March 19-22, 2017, San Francisco, CA, USA.Piscataway： IEEE Press, 2017： 1-5.

[12]SCHAICH F, WILD T.Waveform contenders for 5G — OFDM vs.FBMC vs.UFMC[C]//2014 6th International Symposium on Communications, Control and Signal Processing (ISCCSP),May 21-23, 2014, Athens, Greece.Piscataway： IEEE Press,2014： 457-460.