Sylvester矩阵方程的解空间
曾庆怡
(韶关学院 数学与统计学院,广东 韶关512005)
设A,B分别是复数域C上的m,n阶矩阵,C为m×n矩阵,矩阵方程AX+XB=C称为Sylvester矩阵方程.该方程是从应用数学和控制论的有关领域中产生.Sylvester矩阵方程在控制论、信号处理、模式识别、滤波理论、图形处理、微分方程数值解法等方面都有重要的应用.
关于该矩阵方程的解法有很多种,Sylvester方程在C=O的特殊条件下一定有解,X=O就是一个解.该方程有没有非零解就变成高等代数考研真题中常出现的问题.本文就该特殊方程有无非零解的条件做比较系统的综述,讨论有非零阶的条件以及其解空间的维数问题,不对方程的具体解法问题进行讨论.
本文中Jn(a)表示主对角线元素全是a的n阶Jordan矩阵(上三角矩阵),E表示单位矩阵,而Mn(F)表示数域F上的全体n阶矩阵构成的线性空间.
1 矩阵方程AX=XB的解空间的维数
设A,B分别是数域F上的m,n阶矩阵,X是n×m矩阵,V表示数域F上所有的n×m矩阵关于矩阵的加法和数乘构成的线性空间,显然W={X∈V|AX=XB}是V的子空间.那么如何求dimW?
命题1 设A,B是复数域上的n阶矩阵.证明A与B无公共特征根的充要条件是关于X的矩阵方程AX=XB只有零解.
证 必要性.设A,B无公共特征根,则A,B的特征多项式f(λ)与g(λ)互素,于是存在多项式 u(λ),v(λ)使得 u(λ)f(λ)+v(λ)g(λ)=1,从而 g(A)v(A)=E,即 g(A)可逆.由 AX=XB,得到 g(A)X=Xg(B)=O,从而 X=O.
充分性.设 AX=XB 有公共特征根,由|λE-B|=|(λE-B)T|=|(λE-BT)|知 A,BT也有公共特征根 λ.设 Aα=λα,BTβ=λβ,且令 X=αBT,则 X≠O,且 AX=AαBT=λαβT=α(λβT)=αβTB=XB,矛盾!
引理 1 令A=Jn(a),B=Jm(a),W={X∈V|AX=XB},则 dinW=min{n,m}.
证 不失一般性,设a=0令C=(cij)∈W,注意Jn(0)C可以看做是将C的行向上推一行(行变换),最后一行补0,而CJm(0)可以看做是将C的列向右推一列,第一列补0.因此Jn(0)C=CJm(0)的充要条件是cij=ci+1,,j+1,ci1=cnj=0,i≠1,j≠m,即C是每条与主对角线平行的元素完全相同的上三角矩阵.比如n=2,m=3和n=3,m=2对应C的分别是:
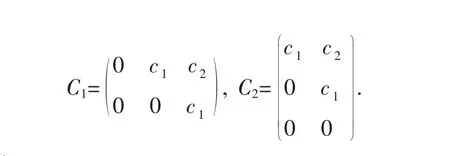
所以C的元素可以这样填,从右上角开始,每一条与主对角线平行的元素填相同的元素,依次往左边填,当斜线经过左上角或右下角的时候为止(当n>m时,斜线先经过左上角,而当n<m时,先经右下角).因此dimW=min{n,m}.
因为 A=Jn(a)的最小多项式是 mA(x)=(x-a)n,而 B=Jm(b)的最小多项式是 mB(x)=(x-b)m.当 a≠b时,W={O},因此 dimW=0;当 a=b时,dimW=min{n,m},即 dimW 等于 mA(x)与 mB(x)的最大公因式的次数.
推论1 设A=Jn(a),B=Jm(b),则dimW等于A的最小多项式mA(x)与B的最小多项式mB(x)的最大公因式的次数.
现在考虑一般情况,假设A,B的特征值全在F内,A,B的Jordan标准形分别是:

这里a1,a2,…,ak未必两两不同,n1+n2+…+nk=n;而 b1,b2,…,bs也未必两两不同,m1+m2+…+ms=m.此时如何求dimW?
任取C∈W,并对C做分块:
则由AC=CB可得:

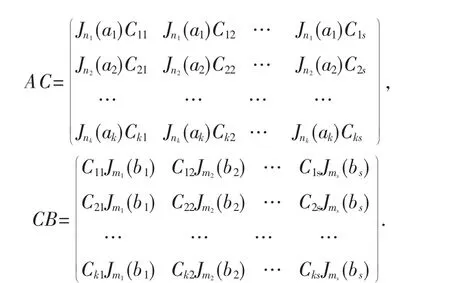
比较可得
令则 Wij是的子空间,且 dimWij等于与的最大公因式的次数.因为每个Cij是独立的因此可得定理1.
定理1 设n阶矩阵A的初等因子是(x-a1)n1
,…,(x-ak)nk
,而m阶矩阵B的初等因子是(x-b1)m1
,…,令 dij表示的最大公因式的次数,则
例1 设A=diag(J2(1),J3(1),J2(2)),B=diag(J3(1),J2(3),J3(2)),则dimW=7.
解 A的初等因子是(x-1)2,(x-1)3,(x-2)2,而B的初等因子是(x-1)3,(x-3)2,(x-2)3,按定理1计算可得dimW=7.
设A=diag(J2(1),J3(1)),是5阶Jordan矩阵,A有两个线性无关的特征向量,W={B∈Mn(F)|AB=BA},由定理1可以得到dimW=9>5.现在设A,B分别是阶矩阵n,m,C为 n×m矩阵,矩阵方程AX-XB=C有解X0,如何求该方程的一般解?
定理2 设A,B分别是阶矩阵n,m,C为n×m矩阵,矩阵方程AX-XB=C有解X0.设W表示AX-XB=O的解空间,dimW=t,而X1,X2,…,Xt是W的一组基,则AX-XB=C的一般解可以表示为:

证 设Y是AX-XB=C的任意一个解,则:

即Y-X0∈W,因此Y-X0可以由X1,X2,…,Xt线性表示,即:

定理2类似于非齐次线性方程组的解的结构定理.
推论2 设A,B分别是阶矩阵n,m,C为n×m矩阵,矩阵方程AX-XB=C有解X0,则该矩阵方程有唯一解的充要条件是A,B没有公共特征值.[厦门大学,2015]
2 AX=XA的解空间
考虑更特殊的情形,即A=B,此时,由命题1 AX=XA一定有非零解,那么W={X∈Mn(F)|AX=XA}的结构怎样?
引理2 设J=Jn(0)为n阶Jordan矩阵,A为n阶矩阵,则AJ=JA的充要条件是存在次数不超过n-1的多项式f(x)使得A=f(J).
证 必要性.设AJ=JA,A=(aij),直接计算可得:

比较可得:
令f(x)=a11+a12x+a1nxn-1,则f(J)=A.
充分性可证.
注:如果J=aE+Jn(0),则AJ=JA等价于AJn(0)=Jn(0)A,因此存在次数不超过n-1的多项式f(x)使得A=f(Jn(0))=f(J-aE).此时取g(x)=f(x-a)即可.
引理 3 设 f1(x),f2(x),…,fk(x)是 k个多项式,其中 deg(fi(x))≤ni-1而 Ji=Jni(ai)为 ni阶 Jordan 矩阵,这里a1,a2,…,ak互不相同,Bi=fi(Ji),i=1,2,…,k,则存在多项式f(x)使得f(Ji)=Bi.
证 因为Ji的零化多项式是mi(x)=(x-a)ni,由于a1,a2,…,ak两两不同,因此m1(x),…,mk(x)互素.
用归纳法.当k=2时,存在u1(x),u2(x)使得u1(x)m1(x)+u2(x)m2(x)=1,因此u1(j1)m1(j1)+u2(j1)m2(j2)=u2(j1)m2(j1)=E;同理,u1(J2)m1(J2)=E.令 f(x)=u2(x)m2(x)f1(x)+u1(x)m1(x)f2(x),则 f(Ji)=fi(Ji),i=1,2.
假设对k-1个满足上述条件的多项式fi(x),i=1,2,…,k-1,结论成立,即存在多项式g(x)使得gi=1,…,k-1.现在设fk(x)是满足条件的第k个多项式,令则对任意 i=1,2…,k-1,m(Ji)=O,且(fk(x),m(x))=1.同上,存在多项式f(x)使得f(Ji)=g(Ji)=fi(Ji),i=1,2…,k-1,f(Jk)=fk(Jk).
定理3 设A=diag(A1,A2,…,Ak)是分块对角矩阵,其中Ai是ni阶矩阵,n1+n2+…+nk=n.对任意n阶满足AB=BA的矩阵B,B也是分块对角矩阵的充要条件是对任意i,j=1,2,…,k,i≠j,Ai和Aj没有公共特征值.
证 充分性.设对任意i,j=1,2,…,k,i≠j,Ai和Aj没有公共特征值.B是任意满足AB=BA的矩阵,对B做分块,并计算如下:

比较可得 BiiAi=AiBii,i=1,2,…,k,而且 AiBij=BijAi,i,j=1,2,…,k,i≠j.由命题 1 Bij=O,i≠j, 因此 B=diag(B11,B22,…,Bkk).
必要性.用反证法.设存在i,j,i≠j使得Ai与Aj有公共特征值,不失一般性,设A1,A2有公共特征值.由命题1,存在n1×n2非零矩阵X使得A1X=XA2,由充分性可得存在不是对角分块矩阵且满足AB=BA条件的矩阵B,矛盾!
引理4 设A是数域F上的n阶矩阵,A的特征值全在F内,a1,a2,…,ak是A的全部不同的特征值,每个特征值只有一个线性无关的特征向量,B是n阶矩阵,则AB=BA的充要条件是存在次数不超过n-1的多项式f(x)使得B=f(A).
证 必要性.因为A的每个特征值只有一个线性无关的特征向量,则存在n阶可逆矩阵P使得P-1AP=diag(J1,J2,…,Jk)=J,其中Ji=Jni(ai),这里ni是ai特征值的重数.由AB=BA可得P-1AP·P-1BP=P-1ABP=P+1BAP=P-1BP·P-1AP.
令C=P-1BP,并对C做分块:

其中Cii是ni阶矩阵.由CJ=JC,以及定理3可得CiiJi=JiCii,i=1,2,…,k,而且C=diag(C11,C22,…,Ckk).由引理2以及后面的注,存在次数不超过ni-1的多项式f(x)使得Cii=fi(Ji),i=1,2,…,k.再由引理3,存在次数不超过n-1的多项式f(x)使得f(Ji)=fi(Ji)=Cii,i=1,2,…,k.因此:

于是,B=PCP-1=Pf(J)P-1=f(PJP-1)=f(A).
充分性可证.
定理4 设A是数域F上的n阶矩阵,A的特征值全在F内,a1,a2,…,ak是A的全部不同的特征值,则每个特征值只有一个线性无关的特征向量的充要条件是对任意满足AB=BA的n阶矩阵B存在次数不超过n-1的多项式f(x)使得B=f(A).
证 必要性.见引理4.
充分性.用反证法.不失一般性,设a1有两个线性无关的特征向量,则存在n阶可逆矩阵P使得P-1AP=diag(J11(a1),J12(a1),J2(a2),…,Jk(ak))=J,这里J11(a1)和 J12(a1)是主对角线,都是 a1的Jordan块.对任意 n阶满足AB=BA的矩阵B,可得P-1AP·P-1BP=P-1ABP=P-1BAP=P-1BP·P-1AP.令C=P-1BP,并对C做分块.

由CJ=JC可得J12(a1)C21=C21J11(a1).由命题1,该矩阵方程有非零的解C21.由于J是上三角矩阵,对任意多项式f(x),f(J)是上三角的,因此存在C使得C不是J的多项式,且CJ=JC,因而B=PCP-1不是A的多项式.事实上,如果存在多项式f(x)使得B=f(A),则C=P-1BP=P-1f(A)P=f(P-1AP)=f(J),矛盾!因此A的每个特征值只有一个线性无关的特征向量.
一般的,如果n阶矩阵A的某一个特征值的初等因子至少有两个,或者线性无关的特征向量至少有两个,令 W={B∈Mn(F)|AB=BA},则因此dimW=n的充要条件是A的每个特征值只有一个线性无关的特征向量.
推论3 设A是数域F上的n阶矩阵,A的特征值全在F内.定义n阶矩阵空间Mn(F)的线性变换σ(X)=AX-XA,∀X∈Mn(F).则以下命题等价:(1)A的每个特征值只有一个线性无关的特征向量;(2)dim ker(σ)=n;(3)dim Im(σ)=n2-n;(4)对任意 B∈ker(σ),存在次数不超过 n-1 的多项式 f(x)使得 B=f(A).
最后,文献[3]证明了若A的Jordan标准形中没有纯数量矩阵的对角块,那么与它可交换的矩阵B必可表示为A矩阵的n-1次多项式,其中n为A矩阵的阶数.这个结论是错误的.反例如下.
例2 设A=diag(J3(0),J2(0))为5阶Jordan矩阵,则A没有纯数量矩阵的对角块.设B是 5阶矩阵,且AB=BA,对做分块:

比较可得


其中b,c,d,e≠0,则AB=BA.由于A是上三角矩阵,对任意多项式f(x),f(A)都是上三角的,B不可能是A的多项式.矛盾!
[1]王萼芳,石生明.高等代数[M].3 版.北京:高等教育出版社,2003.
[2]HOM R A,JOHNSON C R.矩阵分析(Matrix Analysis)[M].张明尧,张凡,译.2 版.北京:机械工业出版社,2014.
[3]钱微微,蔡耀志.论矩阵可交换的充要条件[J].大学数学,2007,23(10):27-31.
Abstract:In this paper,using Jordan theory and theory of minimal polynomial,we discuss the special Sylvester matrix equation AX=XB,which has nonzero solutions with necessary and sufficient condition and the structure and property of solution.A theorem of dimension of solution space has been given.Finally,the structure of solution space of the more special matrix equation AX=XA has been discussed.
Key words: Sylvester matrix equation; Jordan matrix;solution space

