基于小波减噪的基音检测改进算法

赵 发,孙瑞霞

(安徽工程大学电气工程学院，安徽 芜湖 241000)

基音检测是指对语音信号基因周期或频率的这一特征的检测[1]699，在语音识别、语音编码、语音合成等语音应用方面具有非常重要的作用[2]223。目前基音检测存在的主要问题是，当受噪声影响时，带噪语音信号的信噪比急剧下降，从而导致基音检测准确度降低[3-4]163。针对此问题，目前国内外采用的方法主要有两类：直接法和间接法。其中，直接法是指对带噪语音信号直接利用相关算法进行基音检测；如文献[2]223提出一种新的基于经验模式分解的平均幅度函数与自相关函数加权的基音检测算法。文献[3]163提出的类谐波积谱基音周期检测算法。间接法是指对带噪语音信号进行减噪处理，然后再进行基音检测。如文献[1]700通过基于听觉掩蔽的多频带谱减的方法对带噪的语音信号进行语音增强，再利用能零积和能零比的多门限法对其进行基音检测。直接法由于对噪声不进行预处理，所以对基音检测的准确度提高有限。间接法采用谱减法对带噪语音信号进行减噪处理，但由于谱减法算法具有自身的局限性，对平稳的信号谱减效果较好，而语音信号具有一定的非平稳性，所以用谱减法就会产生一定的检测误差。基于上面的分析，本文利用小波变换在非平稳信号中的有效应用，提出一种基于小波减噪[5-7]和改进自相关函数的基音检测算法，该算法通过小波变换来对带噪语音信号进行减噪，然后再进行改进的自相关函数来进行基音检测。

1 小波减噪

小波减噪是利用噪声与语音信号的特征区别，首先将噪声和语音信号变换到小波域后，然后将噪声对应频带的小波系数置零，利用语音信号的小波系数进行重构还原语音信号，从而达到减噪的目的。

设语音信号表达式为s(t)，噪声信号表达式为n(t)，带噪语音信号为两种的叠加信号f(t)，即

f(t)=s(t)+n(t)

(1)

然后对此带噪语音信号进行离散小波变换

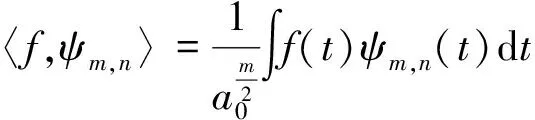
(2)

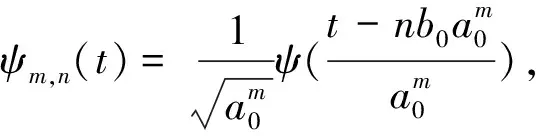
(3)

小波语音减噪的原理框图如图1所示。

图1 小波语音减噪原理框图

2 改进自相关函数

2.1 基本自相关函数

设语音信号的时间序列为x(n)，加窗分帧处理后得到的第i帧语音信号为xi(m)，下标i表示第i帧，设每帧帧长为N，xi(m)的短时自相关函数[8]定义为

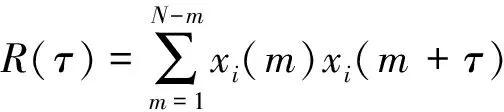
(4)

式中：τ是时间的延迟量。

语音信号可以看做是浊音与清音的结合，因为浊音具有准周期性，而清音不具有周期性，可以利用求自相关把浊音的周期检测出来，检测出的浊音周期可以看做是语音信号的基音周期[9]。通过计算原始语音信号和延迟τ后的语音信号之间的自相关函数，如果R(τ) 具有最大值，则τ即为信号的基音周期。图2为一帧语音信号波形以及对应的归一化自相关函数波形，从图中可以看出，当τ=0 时，归一化自相关函数具有最大值为1，τ≠0时，幅值都小于1。在一帧语音的归一化自相关函数计算中有一个最大值，所以当对一个语音信号求基音周期时，统计帧与帧之间的最大峰值之间的延迟距离即为基音周期，但需注意图2中归一化函数延迟量是以样点数为单位，当采样频率为fs时，每个样点的延迟量为1/fs，可由此把延迟样点数换算为时间。

样点数/个(a)一帖语音信号波形

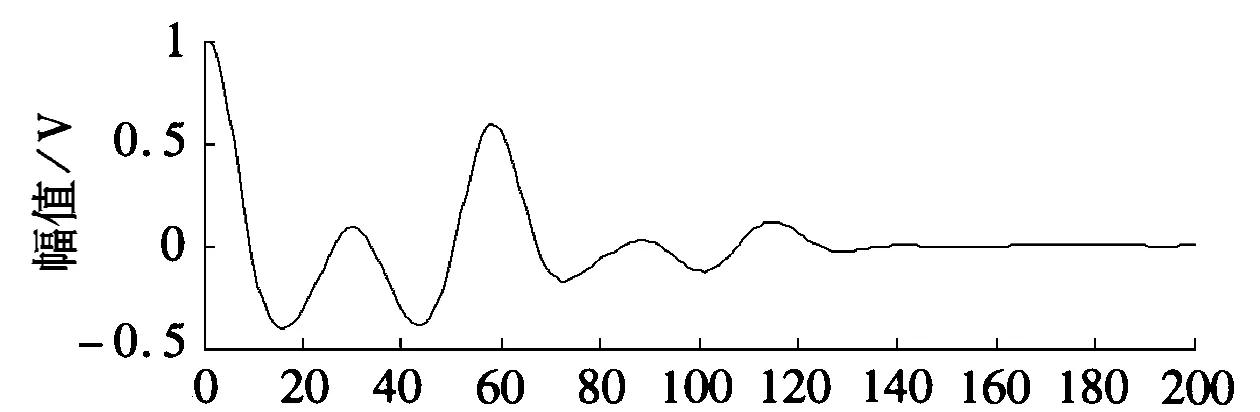
样点数/个(b)归一化自相关函数图2 一帧语音信号波形与相应的归一化自相关函数

2.2 改进自相关函数

用自相关函数进行基音检测[10-11]也存在问题，如声道响应[12]问题，利用自相关进行计算时，由于声道的阻尼振荡，会造成计算出的有一定幅度值的数据太多，从而影响正确选择出由基因周期而计算出的幅度值。所以在进行自相关计算前要对信号进行预处理。目前，最常用的改进方法是先对信号进行非线性处理[13-14]，利用信号本身的特性，共振峰信息主要在幅度比较低的语音段丰富，所以通过对低语音信号幅度段进行非线性处理，从而改善后期进行自相关函数进行检测的性能。中心削波方法[15]是一个非常典型的非线性处理方法，但也有明显的缺点，计算量很大。为此，本文采用对中心削波方法的修正方法，其传递函数为

(5)

图3 三电平中心削波函数

通过图3可以得出，削波器输出在x(n)>CL时为1，x(n)<-CL时为-1，除此之外为0。采用此方法可限定输出的个数，简化计算，只需要简单的逻辑组合，为实时运算创造条件。

3 本文复合算法实现

本文提出的基于小波减噪和改进自相关函数的基因检测算法可分为语音信号的预处理、小波减噪、三电平中心削波自相关函数计算，基因周期和基因频率的提取。具体步骤如下：

1)对带噪语音进行预处理；

2)利用离散小波变换法对带噪语音信号进行变换，得到对应的的小波系数；

3)自适应阈值处理；常规的阈值处理一般采用固定阈值[16-17]，但采用固定阈值时，大尺度上的信号有一部分被滤除掉，从而引起较大的失真。本文采用自适应阈值，使其随尺度的增大而减小；即

(6)

式中：j为当前的分解层数即尺度。上式为试验得到的经验公式，调节常数C用以得到最佳的输出SNR；

4)由处理后的小波系数估值重构语音信号；

5)对减噪后的语音信号进行端点检测；

6)利用三电平中心削波自相关函数进行基因周期和基因频率的提取。

4 实验结果与分析

首先，在安静环境下，自己录制一段语音，内容为“电子信息工程”，此语音可视为纯语音信号。其次，对该语音信号添加高斯白噪声形成不同信噪比的带噪语音信号。图4和图5是基于小波变换和三电平削波自相关函数的基因检测算法在信噪比是0dB和-5dB时的基音检测相关波形；图6和图7是没有进行小波变换的单纯三电平削波自相关函数法的基音检测相关波形。图中的竖实线部分是有效语音的起始点，竖虚线部分是有效语音的结束点。比较在低信噪比条件下本文算法与单纯用改进自相关函数算法的基音检测的性能。从图4和图5可知，经过小波减噪后信噪比都得到了很大的提高，0dB时信噪比提高到10.27dB，-5dB时信噪比提高到6.17dB，经过小波减噪后对信号进行端点检测，然后再进行三电平中心削波自相关函数进行基音检测；基音检测效果较好，没有毛刺现象，其中最后一幅图是把基音频率波形与语谱图进行比较，通过波形可以看出通过本文算法的基音检测频率和语谱图上的基音频率曲线重合度很高。而从图6和图7可知，在SNR=0dB和-5dB时，由于信噪比的下降，单纯三电平中心削波自相关函数法的基音检测频率效果受到很大影响，基音周期的检测出现了毛刺现象，同时比较基音频率波形与语谱图，甚至出现了检测错误的情况，如在0dB时，“程”字没有被检测出来。在更低的-5dB时，“子”和“程”字两个都没有被检测出来。由此可知，本文基于小波减噪和改进自相关函数法的复合基音检测算法在处理低信噪比的带噪语音信号时，首先通过小波变换对带噪语音信号进行减噪，然后再利用改进的自相关函数法进行基音检测。这种复合算法的检测效果比直接用改进自相关函数法进行基音检测的效果好。

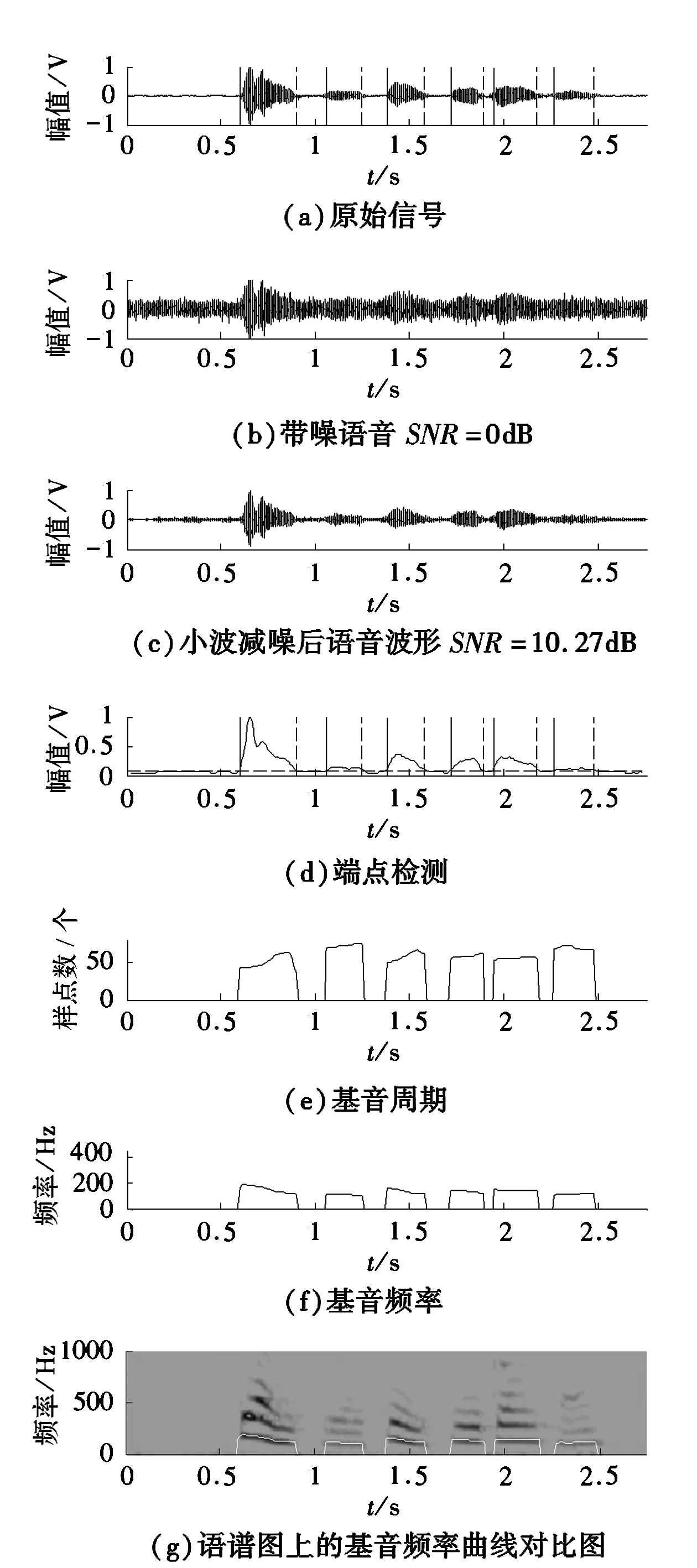
图4 SNR=0dB本文算法

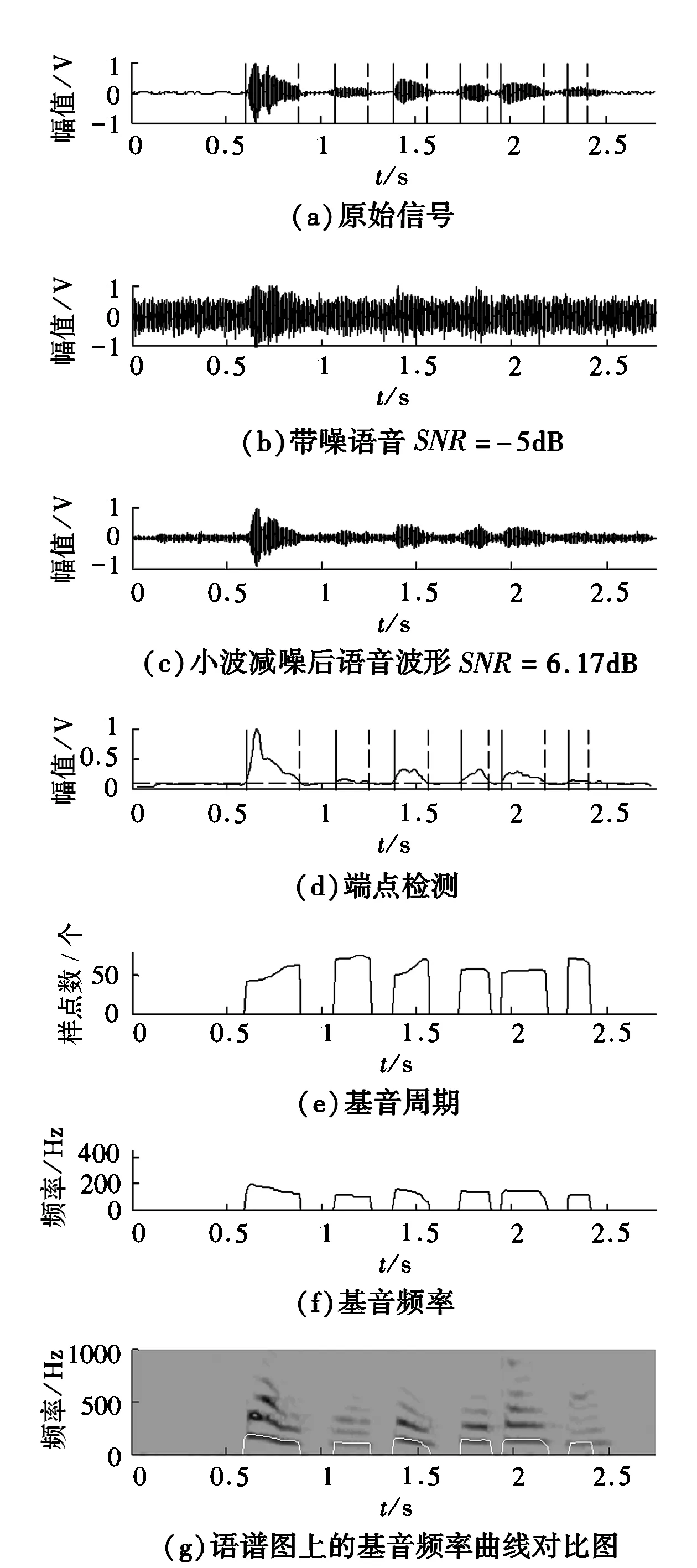
图5 SNR=-5dB的本文算法

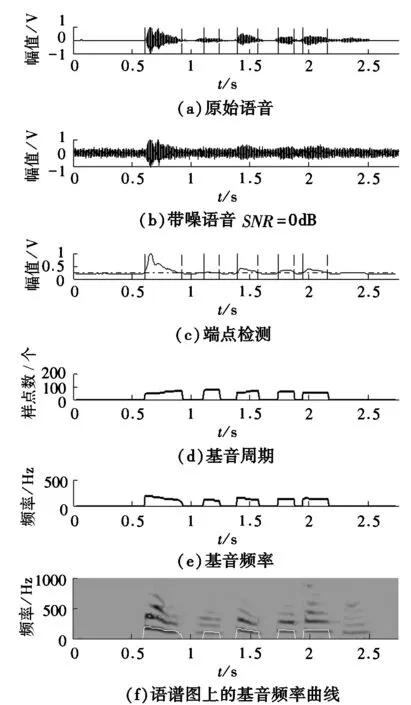
图6 SNR=0dB的改进自相关算法

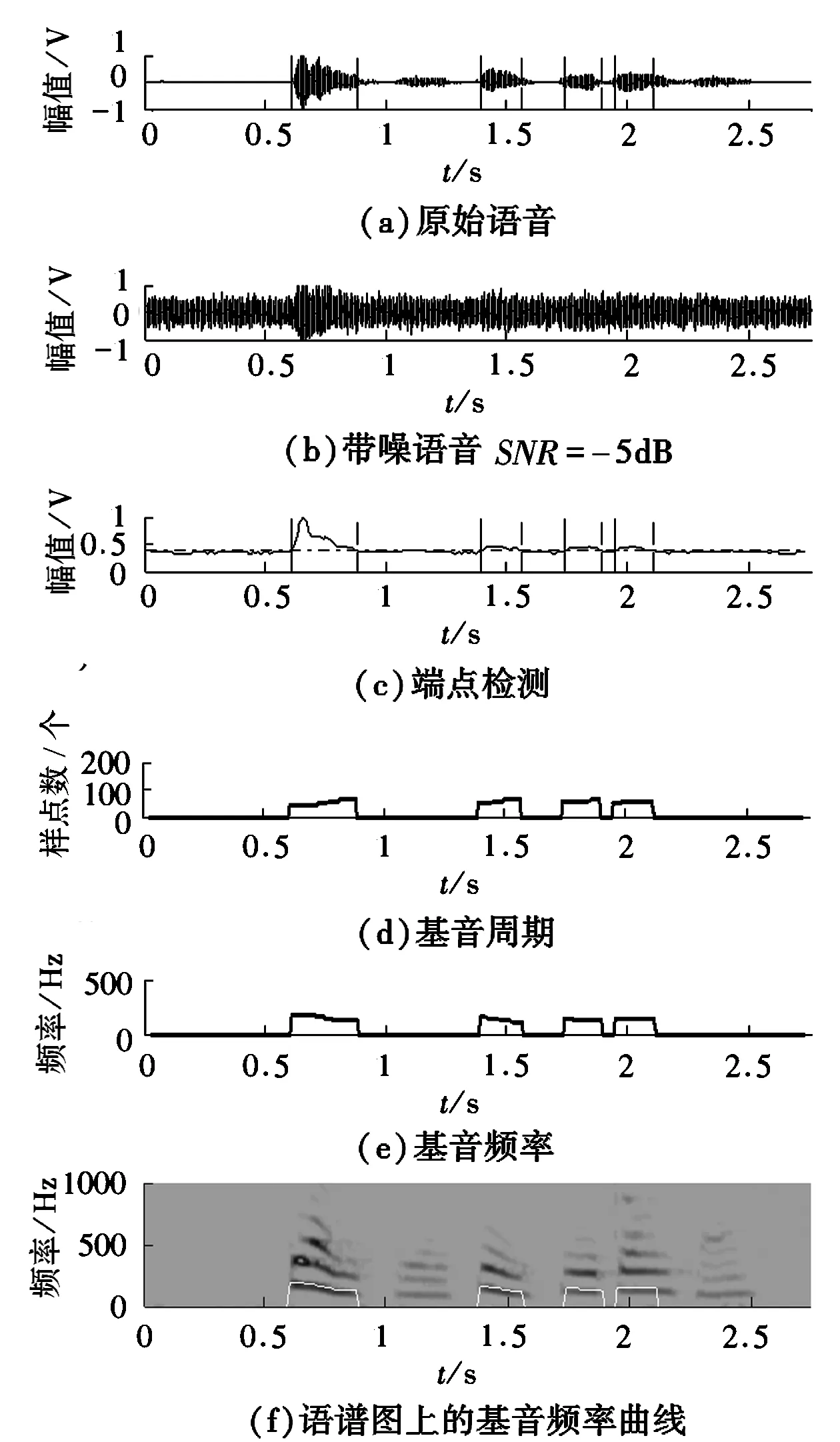
图7 SNR=-5dB的改进自相关算法

5 结论

为了提高含噪语音信号在低信噪比情况下的基音检测准确度，利用MATLAB进行了仿真实验，对不同信噪比的带噪语音分别进行了改进算法的基音检测和未进行小波减噪的基音检测，实验结果表明，利用小波减噪的改进算法在对具有低信噪比的带噪语音进行基音检测时具有更好的准确度。

参考文献：

[1] 徐昕，张天琪，石穗，等.结合语音增强的基音检测改进方法[J].计算机工程与设计，2015，36(3)：699-704.

[2] 潘峥嵘，戴芮，张宁.改进的基音周期检测算法研究[J].计算机工程与应用，2015，51(10)：223-226.

[3] 陈盼弟，黄华，何凌.基于自相关和倒谱法的基音检测改进算法[J].计算机应用与软件，2015，32(1)：163-166.

[4] 梅铁民，付天娇，朱向荣.类谐波积谱基音周期检测算法[J].沈阳理工大学学报，2016，35(2)：14-18.

[5] 薛帅强，陈波，陈菲.改进LVAMDF及综合多因素基音检测算法[J].计算机测量与控制，2016，24(4)：253-256.

[6] ZHAO Y，ZHANG S，LIN X K. Improved Algorithm for Pitch Detection and Harmonic Separation[J]. Applied Mechanics and Materials，2013，24 (9)：753-763.

[7] BAHJA F，DI M J，IBN E，et al. A corroborative study on improving pitch determination by time-frequency cepstrum decomposition using wavelets.[J]. SpringerPlus，2016，5(5)：1-17.

[8] HAMID R T，SEYESD M A. New features for speech enhancement using bivariate shrinkage based on redundant wavelet filter-banks[J]. Computer Speech & Language，2016，35：93-115.

[9] MOHAMED B，AICHA B，NOUREDDINE E. Speech enhancement based on wavelet packet of an improved principal component analysis[J]. Computer Speech & Language，2016，35：58-72.

[10] 沈瑜，党建武，王阳萍，等.加权短时自相关函数的基音周期估计算法[J].计算机工程与应用，2012，48(35)：1-6.

[11] 徐敬德，常亮，崔慧娟，等.基于频域和时域结合的基音周期提取算法[J].清华大学学报，2012，52(3)：413-415.

[12] 赵祎，张盛，林孝康.一种改进的基音周期提取算法[J].数据采集与处，2014，29(2)：304-308.

[13] 王民，曹绘，要趁红.一种改进的小波变换基音检测算法[J].重庆邮电大学学报，2012，24(3)：283-287.

[14] 杨青，马蕙，籍仙荣.利用自相关函数和双耳自相关函数分析对交通噪声特征参量的提取[J].声学学报，2014，39(5)：624-632.

[15] 杨青，马蕙，于博雅.交通噪声时空因素分析的初探[J].噪声与振动控制，2013，33(2)：60-63.

[16] 赵萍. 语音信号的自相关基音周期检测[J].上海电力学院学报，2011，27(3)：297-300.

[17] 闫靓，陈克安.基于双耳自相关函数的车辆噪声烦恼度研究[J].声学学报，2011，36(1)：43-50.