Rydberg原子的微波电磁感应透明-Autler-Townes光谱∗

樊佳蓓 焦月春2) 郝丽萍 薛咏梅 赵建明2) 贾锁堂2)

1)(量子光学与光量子器件国家重点实验室,山西大学激光光谱研究所,太原 030006)

2)(山西大学极端光学协同创新中心,太原 030006)

1 引 言

电磁场可用来操控光在介质中的传播特性,具有广泛的应用前景[1].其中一个重要的应用是电磁感应透明(EIT)效应[2],即原子与电磁波作用时产生量子相干效应,使弱探测光在原子共振处的吸收减小甚至于变为完全透明的现象.利用EIT效应可实现光速的减慢[3]、磁场的测量[4]和光存储[5]等.Autler-Townes(AT)分裂,也称作AC Stark效应[6,7],指电磁场共振或近共振作用于原子或分子的跃迁时,导致相应的吸收谱线产生分裂的现象,是由Autler和Townes[8]在研究微波场的Stark效应时提出的.近年来,人们在原子蒸气和超冷原子样品中也开展了AT分裂的研究[9,10].

Rydberg原子具有极大的极化率(约n7,n为主量子数)和微波跃迁偶极矩(约n2)[11],对外电场极其敏感[12],可实现基于原子的外场测量.英国Adams研究组利用Rydberg EIT效应实现了Rydberg原子的无损探测[13],研究了Rydberg原子对外场的效应,获得了巨大的电光系数[12];射频场缀饰[9]的Rydberg EIT光谱[14]可以实现微波电场[15]、毫米波[16]以及静电场[17]的精密测量.另外,微波场还可以用来耦合对态Rydberg原子,实现共振能量转移[18].Rydberg原子阶梯型系统的EIT效应不仅具有一般Λ-型三能级原子EIT的特性,还携带了Rydberg原子本身的奇异特点,这使得Rydberg EIT效应可用于非线性光学[1]、量子信息和量子纠缠、量子逻辑门[19−22]以及非经典光源[23,24]的制备和精密测量等研究,受到人们的广泛关注.

本文在铯原子蒸气池中,研究了30.582 GHz微波场缀饰的Rydberg原子的EIT-AT光谱.利用EIT-AT分裂的间距和光谱特征实现了微波场强度和非均匀特性的测量,可用于对微波场进行实时监控.

2 实验装置

研究铯原子微波场缀饰的Rydberg原子EIT的实验装置如图1(a)所示.一束λp=852 nm的探测光和一束λc=510 nm的耦合光沿x方向相对入射作用于直径为20 mm,长为50 mm的圆柱形玻璃铯泡上.探测光作用于6S1/2(F=4)→6P3/2(F′=5)的跃迁,耦合光作用于Rydberg跃迁6P3/2(F′=5)→50S1/2,形成阶梯型EIT系统,如图1(b)所示.探测光经二向色镜后进入光电探测器,实现Rydberg EIT-AT信号的探测.探测光由半导体激光器(DLpro,线宽100 kHz)提供,其输出频率利用偏振光谱稳频[25]的方法锁定在6S1/2(F=4)→6P3/2(F′=5)的共振跃迁处;耦合光由连续可调谐的半导体倍频激光器(TA-SHG110,线宽1 MHz)提供,对应的输出频率由EIT稳频的方法[26,27]锁定在6P3/2(F′=5)→50S1/2的跃迁线上或者波长计监控使其频率在50S1/2能级附近扫描.在距离铯蒸气池15 cm的位置处放置一个极化方向与探测光(或耦合光)的偏振方向平行的微波喇叭天线,其微波信号源的频率调谐到30.582 GHz,以实现相邻Rydberg能级50S1/2→50P1/2的跃迁.探测光和耦合光的腰斑分别为ωp=75µm和ωc=95µm,对应的功率分别为2.5µW和70.8 mW.

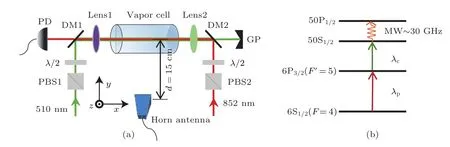
图1 (a)实验装置示意图,λc=510 nm 的耦合光与λp=852 nm的探测光相对作用于铯原子蒸气池中,在与光轴垂直方向距离铯泡15 cm处放置微波喇叭天线,作用于玻璃泡铯原子样品产生EIT-AT效应,其中耦合光与探测光偏振方向沿y轴,微波偏振与光的偏振相同;PD,光电探测器;DM,二向色镜;PBS,偏振分光棱镜;GP,垃圾池;lens1,510 nm透镜;lens2,852 nm透镜;(b)铯原子阶梯型四能级示意图Fig.1.(a)Sketch of the experimental setup.510 nm(λc)coupling and 852 nm(λp)probe laser are counterpropagated into a room-temperature cesium cell,and the horn antenna is placed 15 cm far from cesium cell,which emits the microwave at vapor cell to interact with atom to produce an EIT-AT e ff ect.Polarization of probe and coupling laser is set along y axis,and parallels to the polarization of microwave field.PD,photodiode detector.DM,dichroic mirror;PBS,polarizing beam splitter;GP,garbage pool for a green laser.(b)Diagram of the cesium ladder system.

微波在自由空间传播时,远场条件下的功率密度可表示为

式中,P为微波信号源的输出功率;为增益系数,其中,λ为微波波长,W和H分别为喇叭天线的宽度和高度;d为微波喇叭天线与铯泡轴线中心点的距离,当d=15 cm时满足远场条件,如图1(a)所示.功率密度还可表示为

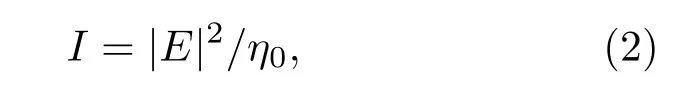
式中,η0=120π Ω表示自由空间的阻抗,E为微波场的电场强度.由(1)和(2)式可得

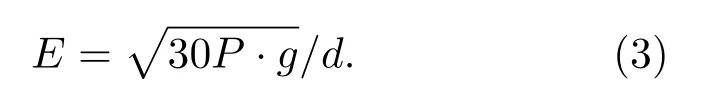
由(3)式可知,微波场的电场E与微波信号源输出功率的平方根成正比.

3 实验结果与分析

实验中,探测光的频率锁定在6S1/2(F=4)→6P3/2(F′=5)的跃迁,耦合光的频率调谐到Ry-dberg 6P3/2(F′=5)→50S1/2跃迁附近,其扫描范围约为500 MHz,可覆盖中间态6P3/2的精细结构能级到50S1/2Rydberg态的跃迁.图2的灰色点表示无微波场,输出为−10.34 dBm(0.09 mW)和1.75 dBm(1.50 mW)时的EIT光谱曲线.无微波场时的EIT谱线如图2(a)所示,主峰为6S1/2(F=4)→6P3/2(F′=5)→50S1/2形成的EIT,在负失谐168 MHz处的小峰是由中间态的超精细结构6P3/2(F′=4)形成的EIT,中间态超精细能级F′=5和F′=4的间隔为251 MHz,考虑Doppler修正因子时6P3/2(F′=5)和6P3/2(F′=4)形成的Rydberg EIT间隔为168 MHz.这里利用超精细结构6P3/2(F′=4)形成的EIT对微波场耦合的EIT-AT光谱分裂进行了定标.

图2(b)和图2(c)分别为微波源输出为0.09和1.50 mW时测量的EIT-AT谱线.

图2 耦合光在6P3/2(F′=5)→50S1/2的Rydberg态跃迁附近扫描时的实验测量(灰色点)和由四能级密度矩阵计算(实线)的EIT谱线 (a)不加微波电场时的EIT光谱,失谐−168 MHz的小峰是由于中间态6P3/2(F′=4)的超精细结构形成的EIT光谱;(b),(c)微波场为0.09,1.50 mW时的EIT-AT分裂光谱Fig.2.EIT spectrum when coupling laser scan near transition of 6P3/2(F′=5)→ 50S1/2,symbols for experimental measurements and solid lines for simulations:(a)EIT spectrum without microwave field,and the signal at detuning of−168 MHz is produced due to EIT spectrum of hyper fine structure of 6P3/2(F′=4)level;(b),(c)EIT-AT spectra at microwave field of 0.09 and 1.50 mW,respectively.

由图2可知,30.582 GHz的微波场共振作用于50S1/2→50P1/2的跃迁时,Rydberg能级产生微波AT分裂致使EIT光谱发生分裂,形成EIT-AT分裂光谱,其分裂间隔与所加微波场的Rabi频率成正比.

图1(b)所示光与原子相互作用的四能级系统的密度矩阵方程表示为

其中,H为四能级系统的哈密顿量,Γ为考虑系统衰减(decay)过程的Lindblad算符.数值求解方程(4)即可获得Rydberg EIT-AT分裂光谱,如图2中的实线所示.当不加微波场时,四能级原子系统退化为三能级EIT系统,详细的理论模型参见文献[28].理论计算较好地再现了三能级EIT信号和微波耦合形成的EIT-AT分裂光谱.

微波电场作用于相邻的Rydberg能级时对应的Rabi频率ΩMW表示为

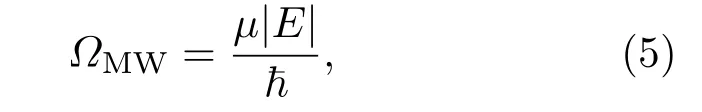
其中,µ表示微波电场耦合的Rydberg态|50S到|50P的跃迁矩阵元,|E|为微波电场幅值,～为约化普朗克常数.微波场耦合Rydberg能级产生的AT分裂大小等于Rabi频率ΩMW,即:2π∆f=ΩMW[8].利用Rydberg能级阶梯型EIT可以测量微波场导致的AT分裂,进而提供测量微波电场强度的方法[15]:

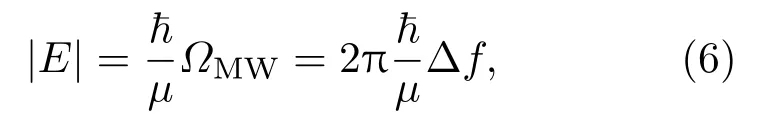
其中∆f表示AT分裂的大小.由(6)式可见,电场强度与AT分裂的大小成正比.

然而,当进一步增加微波电场时,EIT-AT光谱线分裂为4个峰,如图2(c)中的黑色实线所示.本文所用的线偏振激光场耦合的6S1/2(F=4)→6P3/2(F′=5)→50S1/2三能级系统与图1(a)所示的线偏振极化的微波场作用时,由方程(5)可知,EIT-AT光谱能且只能形成两个峰.图2(c)所示的结果表示形成了两对AT分裂光谱,分别对应于不同的微波场Rabi频率和电场强度.分裂间隔较小的AT光谱对应的微波电场较小,反之亦然.分析产生多峰的原因是实验所用的铯池较长,由于铯池中微波场的不均匀性,使原子与光作用的轴线上感受并测量的微波场不同,从而形成EIT-AT多峰光谱.在微波电场较小时,由于EIT线宽的限制没有形成多峰光谱,如图2(b)所示.但当仔细观察图2(b)的双峰光谱时,发现实验测量的EIT-AT光谱的展宽大于理论计算结果,主要表现在AT光谱内侧谱线的展宽上,这里的光谱展宽是由场的非均匀产生的.随着信号源输出功率的增加和铯池中微波电场的增加,当铯池中微波场的非均匀性导致的AT分裂大于EIT线宽时,会观测到明显的多峰光谱结构,形成多峰EIT-AT光谱特征.

为了进一步研究微波场缀饰的Rydberg能级的EIT-AT分裂特性,我们进行了一系列实验测量.图3为当信号源输出功率从0.01 mW变化到10 mW时的谱线分裂结果,可以明显地看出EITAT分裂光谱随信号源输出功率的变化情况.随着电场强度的增加,EIT光谱线由没有微波场时的一个峰分裂为两个峰,再分裂为4个峰,且谱线间隔与电场强度成正比.

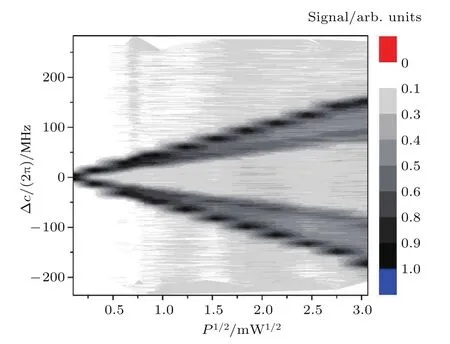
图3 微波信号源的输出功率从0.01 mW到10 mW变化时测量的EIT-AT分裂光谱Fig.3.Spectral splitting when intensity of microwave field varies from 0.01 mW to 10 mW.

利用Rydberg原子EIT-AT分裂的多峰光谱可以测量并分析电场的非均匀特性.在热原子蒸气池中,由于场的非均匀性,轴线上的铯原子感受到的微波场不同,而探测器探测到的信号为光与原子作用轴线上产生的AT分裂信号的叠加,所以观测到多峰结构的谱线.根据以上分析,我们首先测量了EIT-AT光谱中的两对AT分裂间隔(见图2(c)),分裂间隔较小的AT1对应的电场为E1,间隔较大的AT2对应的电场为E2;然后绘制了AT分裂间距与信号源输出功率平方根的依赖关系曲线,如图4所示,实线表示线性拟合的结果,拟合曲线经过0点表示在电场强度为0即不加微波场时三能级EIT的结果.

由于铯池轴线上微波场的非均匀性,测到两个典型的电场值(对应两组AT分裂).由图4可知,测量的AT1(E1)和AT2(E2)都与信号源输出的微波电场成正比,微波场的分布不随信号源的输出而变化.对于确定的信号源输出功率P,定义铯池处单位长度上微波场的非均匀性表示为

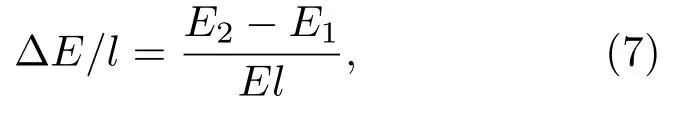
其中,E=(E1+E2)/2表示铯池中微波场的平均值,l为铯池的长度.在本文条件下单位长度场的非均匀度为9.5%.图3所示EIT-AT分裂的光谱特征反映出微波场强度及其分布情况,可用于实现微波场的实时测量和监测.

图4 测量的AT分裂与信号源输出功率的平方根的依赖关系(方形数据表示较大的AT分裂;圆数据表示较小的AT分裂;实线表示线性拟合的结果)Fig.4.Measurements of the AT splitting as a function of microwave power for larger AT splitting(square)and smaller one(circle).The solid lines represent linear fitting to the experiments.

图3和图4的结果也提供了一种提高微波场空间分辨率的方法.基于原子场测量的空间分辨率主要取决于光与原子的作用区域,可分为平行于激光束的轴线方向和垂直于激光束的径向方向.径向的分辨率由激光束的腰斑决定,一般实验中的腰斑为几十微米量级;而轴向的分辨率取决于原子蒸气池的长度.为了减小测量的不确定度,提高测量的空间分辨率,可以选取长度更小的铯泡以提高其空间分辨率.

4 结 论

我们在室温铯原子蒸气池中实现了6S1/2→6P3/2→50S1/2阶梯型三能级系统的Rydberg原子的EIT效应,在此基础上,施加30.582 GHz的微波电场耦合相邻的Rydberg能级,形成AT分裂,且AT分裂间隔随着电场强度的增加线性增加,与微波电场强度成正比.对于本文所用的微波耦合nS1/2-nP1/2的能级结构,多峰EIT-AT光谱由微波场的不均匀性形成,每一对AT分裂对应于一个测量的电场值.由于场的非均匀性产生的EIT-AT光谱的展宽以及多峰结构,降低了微波场测量的精度和空间分辨率.在此,我们提出通过减小铯泡的长度来提高测量空间分辨率的方法.本文的研究成果提供了测量微波电场的方法,EIT-AT光谱特征提供了一种实时监测微波场强度和空间分布的方法,在微波场的测量方面具有很重要的应用前景.

参考文献

[1]Boyd R W 2008Nonlinear Optics(Beijing:Academic Press)p55

[2]Harris S E 1997Phys.Today50 36

[3]Hau L V,Harris S E,Dutton Z,Behroozi C H 1999Nature397 594

[4]Scully M O,Fleischhauer M 1992Phys.Rev.Lett.69 1360

[5]Phillips D F,Fleischhauer A,Mair A,Walsworth R L,Lukin M D 2001Phys.Rev.Lett.86 783

[6]Picque J L,Pinard J 1976J.Phys.B9 L77

[7]Cahuzac P,Vetter R 1976Phys.Rev.A14 270

[8]Autler S H,Townes C H 1955Phys.Rev.100 703

[9]Scully M O,Zubairy M S 1997Quantum Optics(New York:Cambridge University Press)p205

[10]Zhang H,Wang L M,Chen J,Bao S X,Zhang L J,Zhao J M,Jia S T 2013Phys.Rev.A87 033835

[11]Gallagher T F 1994Rydberg Atoms(New York:Cambridge University Press)p11

[12]Comparat D,Pillet P 2010J.Opt.Soc.Am.B27 A208

[13]Mohapatra A K,Jackson T R,Adams C S 2007Phys.Rev.Lett.98 113003

[14]Tanasittikosol M,Pritchard J D,Maxwell D,Gauguet A,Weatherill K J,Potvliege R M,Adams C S 2011J.Phys.B44 184020

[15]Sedlacek J A,Schwettmann A,Kübler H,Löw R,Pfau T,Sha ff er J P 2012Nat.Phys.8 819

[16]Gordon J A,Holloway C L,Schwarzkopf A,Ander-son D A,Miller S,Thaicharoen N,Raithel G 2014Appl.Phys.Lett.105 024104

[17]Barredo D,Kübler H,Daschner R,Löw R,Pfau T 2013Phys.Rev.Lett.110 123002

[18]Bohlouli-Zanjani P,Petrus J A,Martin J D 2007Phys.Rev.Lett.98 203005

[19]Jaksch D,Cirac J I,Zoller P,Rolston S L,Cote R,Lukin M D 2000Phys.Rev.Lett.85 2208

[20]Lukin M D,Flischhauer M,Cote R,Duan L M,Jaksch D,Cirac J I,Zoller P 2001Phys.Rev.Lett.87 037901

[21]Galindo A,Martin-Delgado M A 2002Rev.Mod.Phys.74 347

[22]Isenhower L,Urban E,Zhang X L,Gill A T,Henage T,Johnson T A,Walker T G,Sa ff man M 2010Phys.Rev.Lett.104 010503

[23]Viscor D,Li W,Lesanovsky I 2015New J.Phys.17 033007

[24]Dudin Y O,Kuzmich A 2012Science336 887

[25]Pearman C P,Adams C S,Cox S G,Griffin P F,Smith D A,Hughes I G 2002J.Phys.B35 5141

[26]Jiao Y C,Li J K,Wang L M,Zhang H,Zhang L J,Zhao J M,Jia S T 2016Chin.Phys.B25 053201

[27]Abel R P,Mohapatra A K,Bason M G,Pritchard J D,Weatherill K J,Raitzsch U,Adams C S 2009Appl.Phys.Lett.94 071107

[28]Holloway C L,Simons M T,Gordon J A,Dienstfrey A,Anderson D A,Raithel G 2017J.Appl.Phys.121 233106