基于超二次曲面的颗粒材料缓冲性能离散元分析∗

王嗣强 季顺迎

(大连理工大学,工业装备结构分析国家重点实验室,大连 116023)

1 引 言

颗粒物质是一种复杂的能量耗散体系,其摩擦和黏滞作用可使材料所受冲击载荷的能量有效衰减[1−4].在外载荷的作用下,颗粒间的重新排列调整接触力的传输方向和接触时间,将局部的冲击载荷在空间扩展和时间延长,进而降低冲击强度[5,6].同时,颗粒间的非弹性碰撞引起的飞溅现象,可将系统吸收的冲击能量转化为颗粒自身的机械能,从而达到耗能缓冲的效果,并已得到相应实验的验证[7,8].此外,颗粒物质受冲击后通常会产生塑性变形,局部化的应变场会导致固体状态和流体状态同时存在并相互转化,是颗粒介质类固-液相变的具体体现[9].因此,开展非球形颗粒物质缓冲耗能的研究有助于揭示颗粒材料的内在作用机理及其主要影响因素,并为缓冲减振技术的提升和工程应用提供很好的借鉴.

颗粒材料的缓冲性能与其几何形态有密切关系,而在自然条件或工业生产中均是由非球形颗粒构成的颗粒系统,其在单元排列、动力过程和运动形态等方面与球形颗粒有很大的差异[10,11].大量的实验和数值模拟主要集中在球形颗粒上,而对非球形颗粒系统的宏细观特性研究则相对较少[12,13].近年来,颗粒形状对系统宏观力学性能和动态响应过程的影响引起广泛关注[14,15].为合理地描述具有复杂几何形态的颗粒材料,黏接颗粒单元[16−18]、扩展多面体单元[19−21]、超二次曲面[22−24]等不同的非球形单元及其构造方法不断发展和完善起来.其中,超二次曲面单元可构造凸面体和凹面体的几何形状,并容易地改变函数参数进而控制颗粒的长宽比和表面尖锐度.然而,目前超二次曲面单元的接触力都采用线性近似计算模型,接触刚度也通常采用经验值,在很大程度上影响计算精度.基于球体的赫兹接触模型[25]和基于椭球体表面曲率的接触模型[26]都为超二次曲面单元非线性接触力的计算提供了很好的研究思路.本文在此基础之上考虑超二次曲面单元在不同接触模式下接触点处的曲率半径,进而建立合理的非线性接触模型.

目前,冲击载荷作用下颗粒材料的缓冲耗能研究主要通过对冲击坑的深度、冲击持续时间和冲击物及底板的受力等讨论不同冲击物的速度、角度、质量和粒径以及颗粒床的填充厚度、密集度和颗粒参数如密度、粒径、弹性模量、恢复系数、摩擦系数等因素的影响[27−30].此外,实验研究[31]和离散元计算[32]表明:颗粒厚度是影响球形颗粒材料缓冲性能的重要因素,并存在一个临界厚度;不同表面摩擦系数及颗粒形态间缓冲性能存在明显差异.采用离散单元法(DEM)有助于对冲击过程中颗粒间的接触作用[33]、冲击力的传递途径及能量耗散[34]进行细观分析,从而揭示非球形颗粒材料缓冲耗能的内在机理.

本文基于超二次曲面方程构造非球形颗粒形态,采用离散单元法(DEM)建立不同颗粒形状填充的颗粒床在球形冲击物作用下的数值模型,并通过圆柱体冲击的理论结果和球体冲击的实验结果对计算模型进行验证.在不同颗粒层厚度、颗粒长宽比及表面尖锐度下,通过对底板上冲击力的数值计算,探讨颗粒形状对颗粒材料缓冲特性的影响规律,并通过颗粒材料初始排列的密集度揭示非球形颗粒缓冲性能的内在机理.

2 非球形颗粒的离散元模型

针对非球形颗粒单元的几何特点,这里采用基于连续函数包络的超二次曲面方程描述颗粒的复杂形态,并发展相应的非线性接触模型计算单元间的接触作用,对冲击载荷下冲击物对底板的作用力进行数值模拟.

2.1 基于连续函数包络的超二次曲面单元

基于二次曲面方程扩展得到的超二次曲面模型是描述非球形颗粒的一种普遍方法,其函数形式可定义为[35]

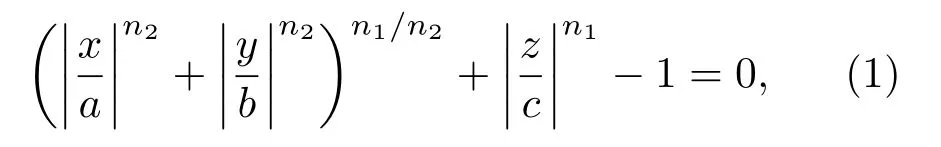
式中,a,b和c分别表示颗粒沿主轴方向的半轴长;n1和n2表示颗粒表面的尖锐度参数.对于n1=n2=2得到球体或椭球体颗粒,n1≫2且n2=2得到柱体颗粒,n12且n22得到块体颗粒.对于n1,n2→∝时,从理论上可以描述具有尖角的颗粒形态,但这种模型往往受搜索算法的限制而难以实现.目前,通过超二次曲面方程构造非球形颗粒的普遍方法是给定参数n1和n2的合理取值范围从而讨论颗粒形状(表面尖锐度)对宏细观特性的影响[15,36,37].因此,本文中n1,n2∈[2,8],且尚需对这种近似模型与具有尖角的真实模型进一步对比和分析.图1显示在超二次曲面方程中改变不同的半轴长和表面尖锐度参数得到不同的单元模型.

图1 三维超二次曲面单元模型Fig.1.Super-quadric elements in three dimensions.

2.2 单元间的接触判断方法

与球形颗粒简单且高效的接触判断相比,非规则颗粒间的搜索时间占整个计算时间的比率会显著增加,其计算效率往往受颗粒形状、边界条件、搜索算法等因素的影响而具有显著差异.本文针对非球形颗粒间接触判断的复杂性,考虑颗粒间不同接触模式下的颗粒取向,采用相应的球形包围盒和方向包围盒(oriented bounding box,OBB),如图2所示.这两种方法可有效减少潜在的接触对,提高程序的计算效率.球形包围盒作为单元间第一次接触的粗判断,其接触理论基于球体与球体间的接触计算,包围球体半径可表示为如果两球体间球心的距离小于其半径和,则接触,否则不接触.OBB作为单元间第二次接触的粗判断,其接触理论基于分离轴算法并考虑颗粒取向和长宽比[38].如果两个几何体在空间向量上的投影发生重叠,则接触,否则不接触.

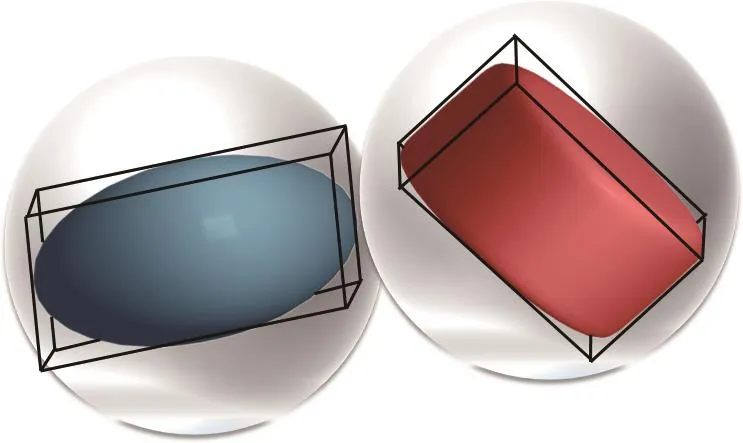
图2 球形包围盒和OBBFig.2.Bounding spheres and oriented bounding boxes.

非线性牛顿迭代方法作为单元间第三次接触判断,该方法将求解单元间最短距离的优化问题转化为非线性方程组进行求解,如图3所示.考虑非球形颗粒接触时表面法向平行且反向,同时基于中间点到两个颗粒表面的几何势能相等建立非线性方程组[39,40]:

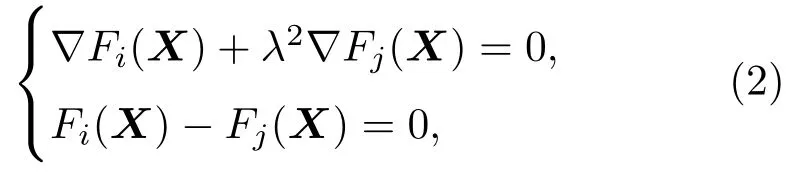
式中,X=(x,y,z)T,Fi(X)和Fj(X)分别表示全局坐标下颗粒i和j的函数方程,∇F(X)表示颗粒表面沿x,y,z方向的外法向,λ2表示两个颗粒间的外法向平行且反向.

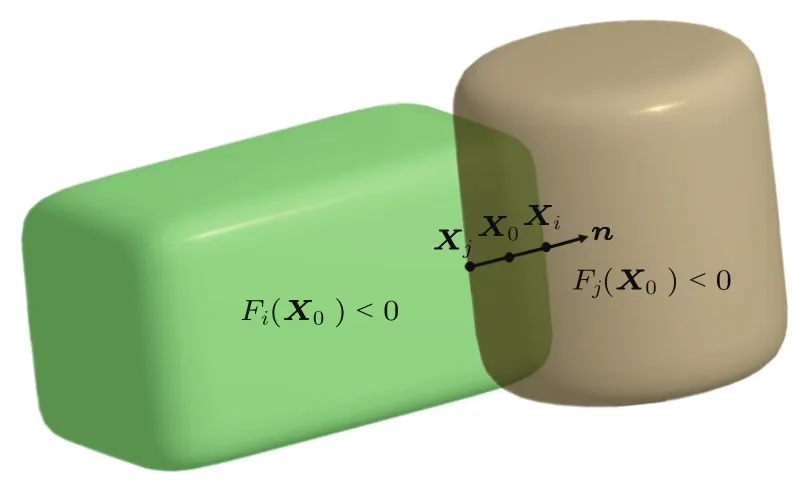
图3 超二次曲面单元间的接触检测Fig.3.Contact detection between super-quadric particles.

由此,牛顿迭代公式可写作:

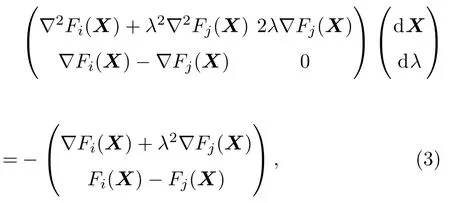
式中,X=X+dX,λ=λ+dλ.如果计算结果X0满足Fi(X0)<0且Fj(X0)<0,则表明两个单元间发生接触,接触法向定义为n=∇Fi(X0)/∥∇Fi(X0)∥.进一步考虑颗粒表面点Xi和Xj满足:Xi=X0+αn和Xj=X0+βn,且未知参数α和β可通过一元非线性牛顿迭代得到:和βk+1=因此,法向重叠量可表述为δn=Xi−Xj.

与单元间的接触搜索类似,单元与固体边界的接触判断通常将边界表示为函数形式,通过联立超二次曲面方程进而建立非线性方程组进行求解.本文中主要固体边界是刚性圆筒,其函数形式可表示为:式中,D0为圆筒直径,H0为圆筒高度,如图4所示.考虑超二次曲面单元i与圆筒接触时表面法向平行且同向,同时基于中间点到颗粒表面和圆筒表面的几何势能相等建立非线性方程组:

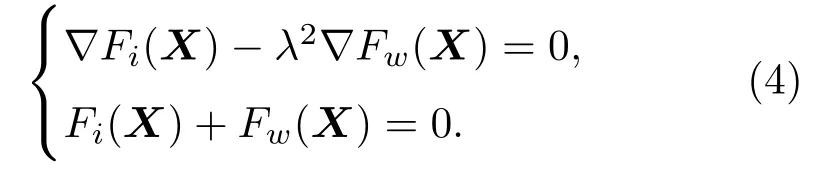
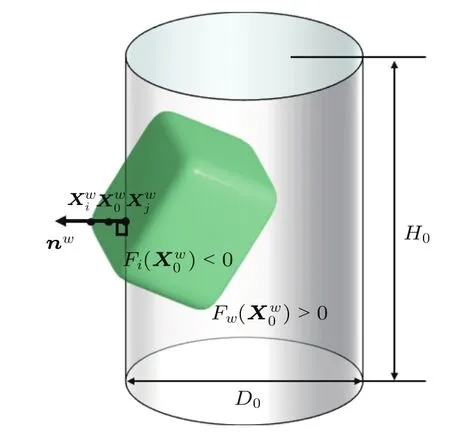
图4 超二次曲面单元与圆筒边界的接触检测Fig.4.Contact detection between a super-quadric particle and a cylinder.

由此,相应的牛顿迭代公式可表示为

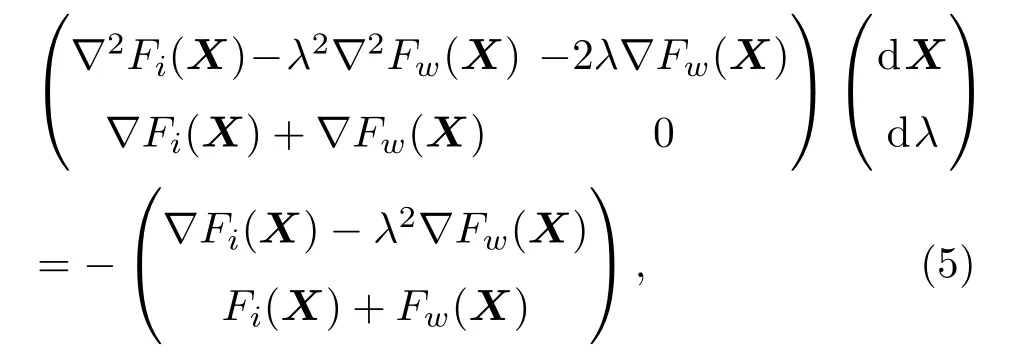
式中,X=X+dX,λ=λ+dλ.如果计算结果满足则表明超二次曲面单元与圆筒边界发生接触,接触法向定义为这里,圆筒表面点可表示为:考虑颗粒表面点且未知量α通过一元非线性牛顿迭代公式得:因此,单元与边界的法向重叠量可表述为

一般而言,求解四元非线性方程组的牛顿迭代算法是影响单元搜索效率及整体计算时间的主要因素,且与颗粒表面尖锐度和长宽比密切相关.随着尖锐度参数n1和n2及长宽比偏离1的指数增加,单元间的搜索效率显著降低;当颗粒接近于球形时,其计算效率最高[23].

2.3 超二次曲面单元间的非线性接触模型

针对超二次曲面单元间不同的接触模式,在传统球形非线性接触模型[25]的基础上,考虑单元间局部接触点处的平均曲率半径[41],进而建立相对合理的非线性接触模型.因此,单元间的接触力主要是由弹性力和黏滞力组成,同时考虑法向力、切向力和滚动摩擦引起的附加力矩.其中,法向作用力Fn可写作:

式中,Kn为两个接触单元的法向有效刚度;δn为法向重叠量;Cn为法向阻尼系数;A为颗粒间的黏滞参数;vn,ij为法向相对速度.这里法向有效刚度Kn、黏滞参数A分别为

式中,Kmean为接触点处的局部平均曲率,其可写作[41]:

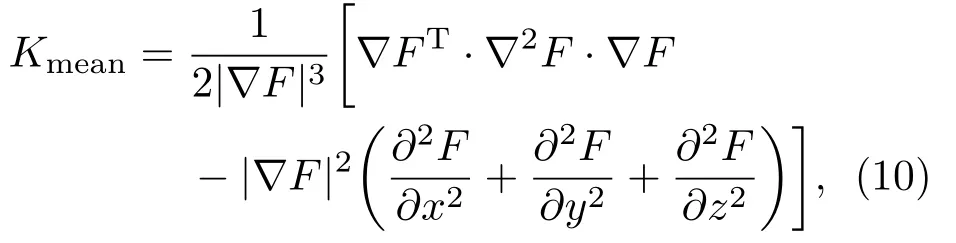
其中,∇F,∇2F分别表示超二次曲面方程的一阶和二阶导函数.

单元间的切向接触力Fs主要由弹性力和黏滞力组成,同时考虑Mohr-Coulomb摩擦定律.则切向弹性力为

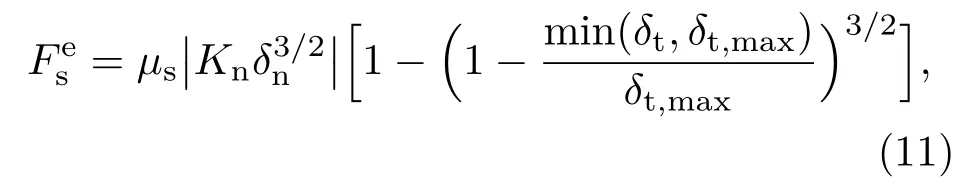
式中,µs为滑动摩擦系数,δt为切向重叠量,δt,max=µs(2−υ)/2(1−υ)·δn.

这里,切向黏滞力为

式中,Ct为切向黏滞系数,vt,ij为单元间切向相对速度.

在单元发生相对转动时,由滚动摩擦引起的力矩Mr可表述为[42]

式中,µr为滚动摩擦系数,即本文中为法向的单位相对转速,可表示为

目前,关于非球形颗粒时间步长的理论研究相对较少,通常是在球形颗粒理论计算的基础上给出合理的时间步长[15,20,26].因此,本文中时间步长的选择是考虑非线性接触模型的球形颗粒单元[43],即

式中,Rmin为颗粒的最小半径,ρ为颗粒密度,G为剪切模量,υ为泊松比.为了保证计算精度和运行效率,Rmin为超二次曲面单元三个方向半轴长的最小值,即Rmin=min(a,b,c),且选择dt6 0.1tmax作为计算步长的依据.

图5 考虑等效曲率的非线性接触模型Fig.5.Non-linear force model with considering the equivalent radius of the particle shape curvature.

3 颗粒材料冲击过程的理论与实验验证

为验证超二次曲面单元间算法和接触模型的有效性,分别对单个圆柱体冲击的理论结果和球体冲击的实验结果与离散元计算值进行对比验证,从而更加合理地模拟冲击力的变化规律.

3.1 圆柱体冲击过程的理论验证

通过超二次曲面模型构造一个理想圆柱体颗粒,给定初始冲击速度下考虑回弹速度和回弹角速度随冲击角度的变化关系,同时假定整个过程无摩擦和重力作用,如图6所示.冲击后的角速度和速度可表述为[44]

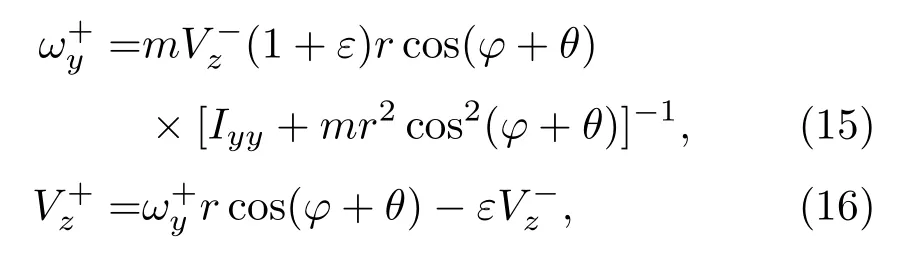
式中,m为圆柱体的质量;为冲击前圆柱体形心的速度;ε为接触点处的回弹系数;φ为接触点与颗粒形心的连线与圆柱体表面的夹角;r为接触点到颗粒形心的距离;θ为颗粒表面与边界的夹角,即冲击角度;Iyy为颗粒绕y轴的转动惯量.在不同角度的冲击过程中,初始冲击速度恒定为1 m/s,回弹系数ε恒定为0.85.当颗粒与边界接触碰撞后,立刻移除边界从而避免在冲击角度过小或过大时产生的二次碰撞.离散元模拟的主要参数列于表1中.

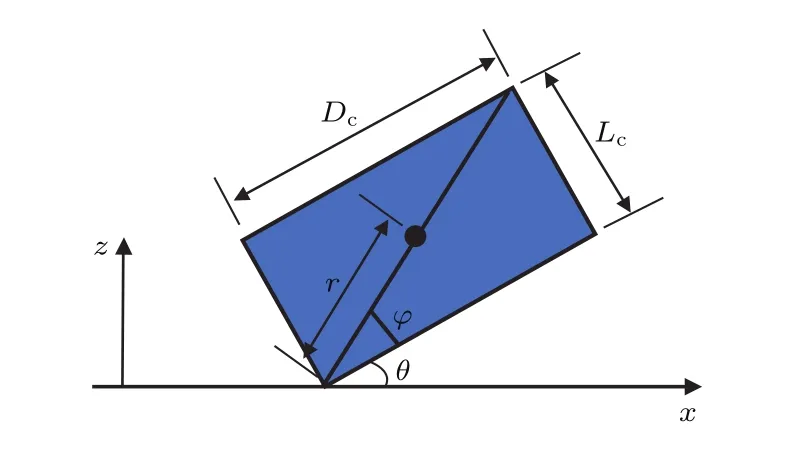
图6 圆柱体冲击的示意图,x-z平面的投影Fig.6.Scheme of cylinder-wall impact,x-z projection.

图7(a)和图7(b)显示了0◦—90◦范围内不同冲击角度下无量纲的回弹速度和角速度与理论结果[44]的对比.值得注意的是,当冲击角度分别为0◦和90◦时,圆柱体与平面的接触不再为点接触.因此,回弹速度的理论解仅与回弹系数相关,而回弹角速度的理论解为零.从图7可以看出,无量纲的回弹速度约为0.85,无量纲的回弹角速度约为0.离散元的计算结果与理论结果[44]基本符合,表明超二次曲面模型和算法适用于模拟非球形颗粒的冲击过程.

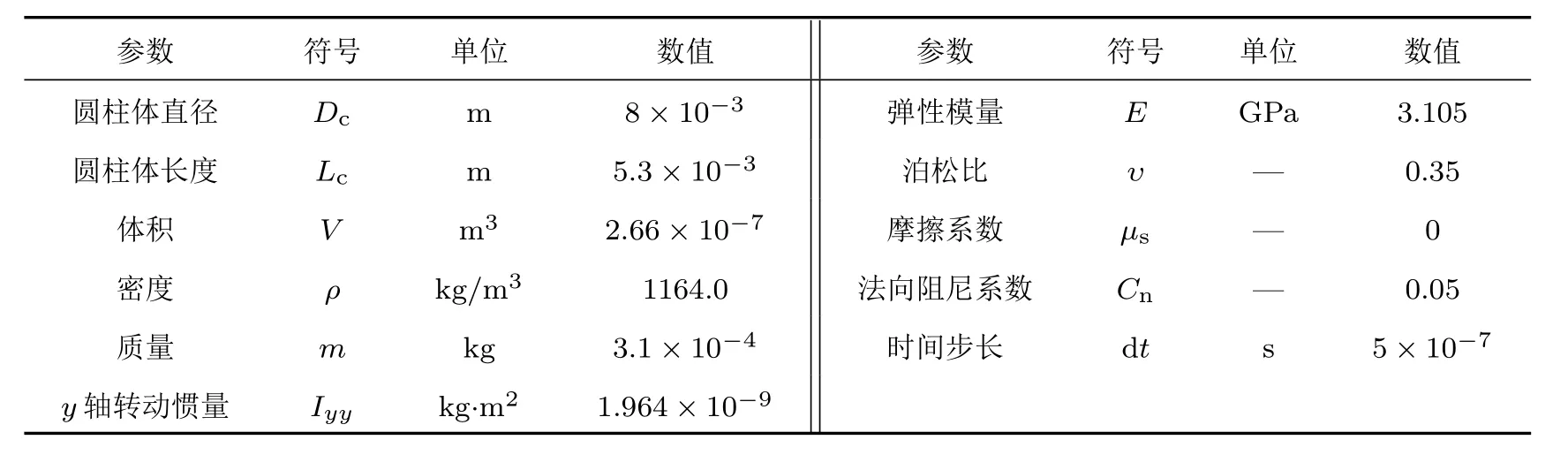
表1 圆柱体冲击离散元模拟的主要计算参数Table 1.DEM simulation parameters of cylinder impact.

图7 圆柱体冲击的解析结果[44]与离散元计算值对比(a)无量纲的回弹速度(b)无量纲的回弹角速度Fig.7.Comparison of cylinder-wall impact between analytical results[44]and DEM simulation results:(a)The dimensionless post-impact translational velocity(b)the dimensionless post-impact angular velocity

3.2 颗粒材料冲击实验的对比验证

为验证超二次曲面离散元计算模型的可靠性,分别对颗粒层厚度为0.5和2.0 cm的球体冲击过程进行数值模拟,并与文献[31]的实验结果进行对比.离散元模拟中球形颗粒单元的粒径按均匀概率密度函数在[4.0 mm,5.0 mm]内随机分布,且均值为4.5 mm,主要的离散元计算参数列于表2中.

当颗粒层厚度分别为H=0.5和2.0 cm时,圆筒底部受冲击力的时程如图8(a)和图8(b)所示.当颗粒层厚度H=0.5 cm时,冲击力峰值与冲击持续时间与实验结果基本符合,但当颗粒层厚度H=2.0 cm时,冲击力峰值低于实验结果,冲击持续时间则大于实验值.同时,实验中冲击力呈现多次波动现象,而离散元结果较为稳定.这主要是由于实验测量的冲击过程中,冲击物引起圆筒底板产生一定的振动,进而出现明显的波动现象.但在离散元模拟中底板通常设成刚性板,因此冲击力的振荡幅度不明显.尽管离散元计算的数值结果与实验结果存在一定的偏差,但冲击力的变化规律是一致的,进一步表明基于超二次曲面模型的离散元方法可以合理地模拟颗粒系统的冲击缓冲过程.

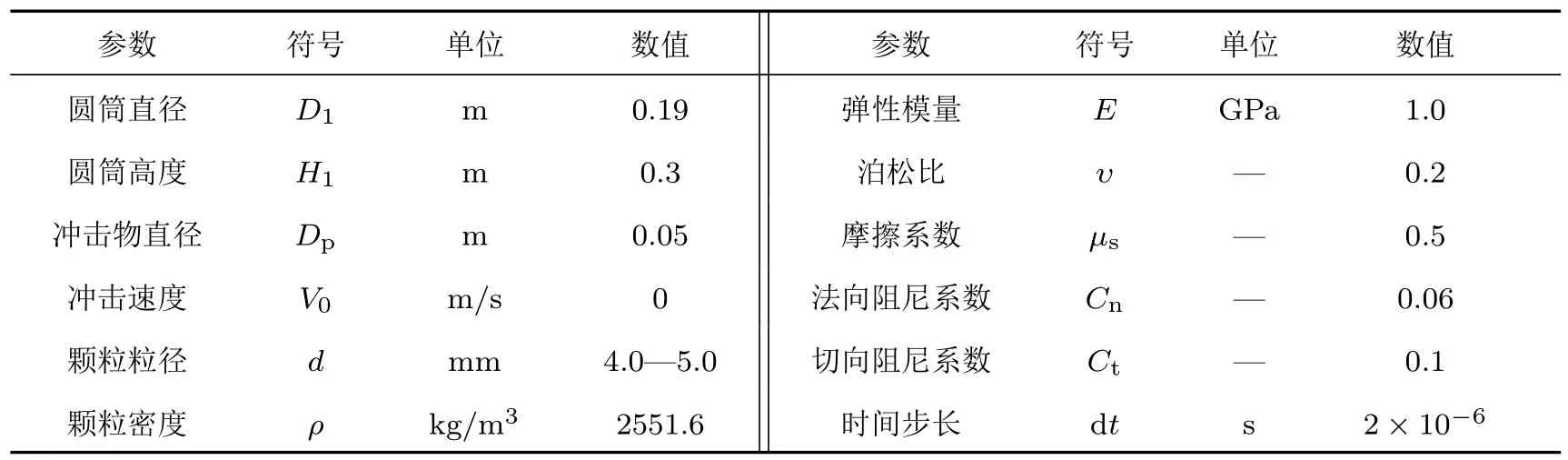
表2 球体冲击离散元模拟的主要计算参数Table 2.DEM simulation parameters of sphere impact.

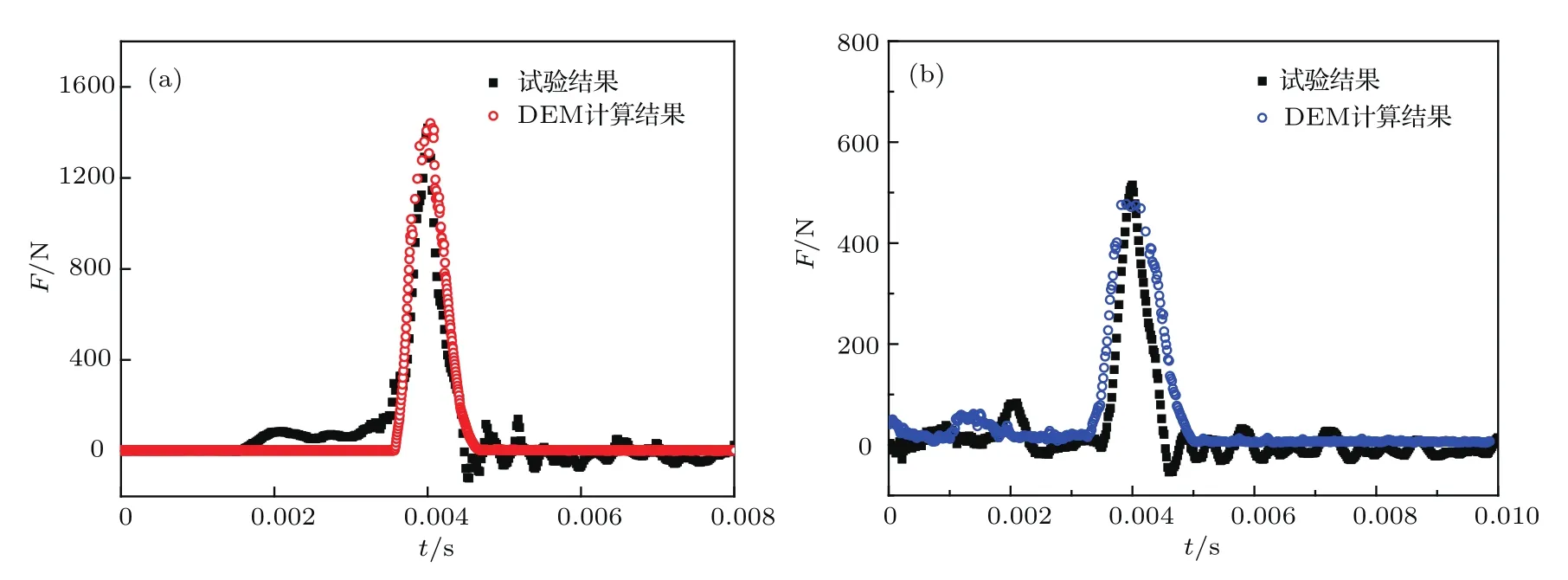
图8 不同颗粒厚度下底板受力变化过程的实验值[31]和离散元计算值对比 (a)颗粒厚度为0.5 cm;(b)颗粒厚度为2.0 cmFig.8.Comparison of impact loads between experiment results[31]and DEM simulation results under different granular thicknesses:(a)H=0.5 cm;(b)H=2.0 cm.

4 颗粒层厚度与形状对缓冲性能的影响

颗粒层厚度和颗粒形状是影响缓冲特性的重要因素.对于圆筒内球形颗粒材料的冲击实验[31]和离散元结果[32]表明,底板所受的冲击力随球形颗粒层厚度的增加而减小,当厚度大于临界厚度时,冲击力峰值变化趋于稳定.同时,非球形颗粒呈现出低流动性、高互锁性等不同于球形颗粒的特殊性质[11].为获得不同颗粒形状间较好的冲击过程,这里令冲击物的初始速度V0=5 m/s,在颗粒层表面上的初始高度H2=30 cm,摩擦系数µs=0.4,法向阻尼系数Cn=0.1,颗粒密度ρ=2500 kg/m3,颗粒半径r0=5 mm,其余计算参数见表2.

4.1 颗粒层厚度的影响

通过超二次曲面方程构造球体、圆柱体、正方体三种不同的颗粒形状,在刚性圆筒中随机产生,通过落雨法生成不同厚度的颗粒床,并在重力作用下颗粒系统保持稳定平衡状态,如图9所示.

当无颗粒填充时,圆筒底部所受的冲击力峰值P0=4.67 kN,当颗粒层厚度H=0.8,1.5,2.5,4.5,9.5 cm时,计算得到的冲击力时程如图10(a)—(c)所示.从图10(a)—(c)可以发现,球体、圆柱体、正方体都呈现类似的冲击特性,即随着颗粒层厚度的增加,冲击力峰值P逐渐减小且冲击持续时间逐渐延长.将三种形状在不同颗粒层厚度下的冲击力峰值进行统计,如图10(d)所示.可以发现,当颗粒层厚度H<7.0 cm时,相比圆柱形和正方形颗粒,球形颗粒的缓冲性能最好,而圆柱形颗粒的缓冲效果优于正方形颗粒.当颗粒层厚度H>7.0 cm时,颗粒层厚度和颗粒形状对缓冲特性的影响不再显著,且趋于稳定.这里称该厚度为临界颗粒层厚度Hc,即Hc=7.0 cm.由于不同颗粒形态的缓冲特性受材料参数、尺度效应、冲击能量等不同因素的影响,因此在不同条件下临界颗粒层厚度通常具有一定差异.

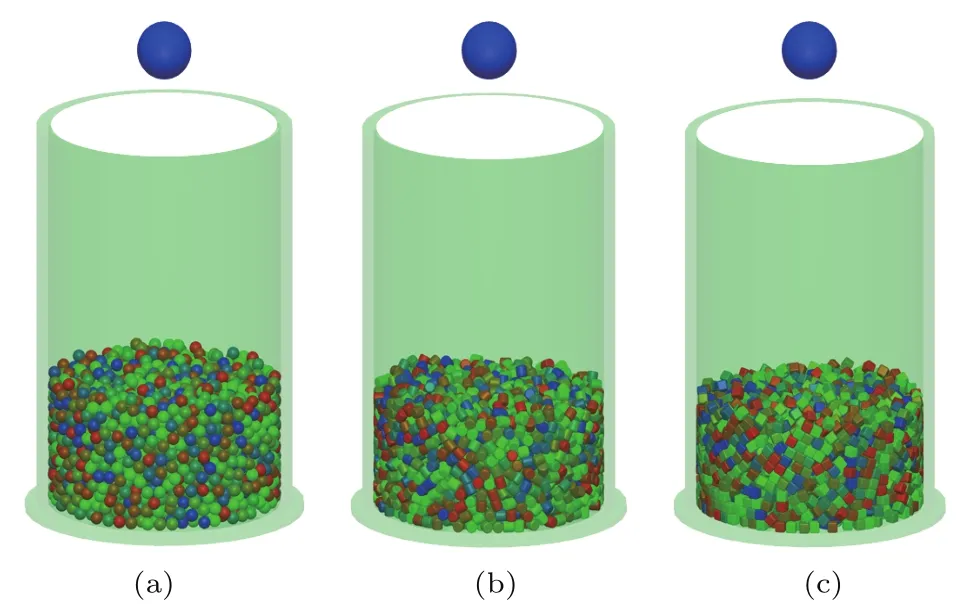
图9 不同形状颗粒材料缓冲特性的离散元模型 (a)球体;(b)圆柱体;(c)正方体Fig.9.Discrete element models of granular materials with different shapes for bu ff er properties study:(a)Sphere;(b)cylinder;(c)cube.

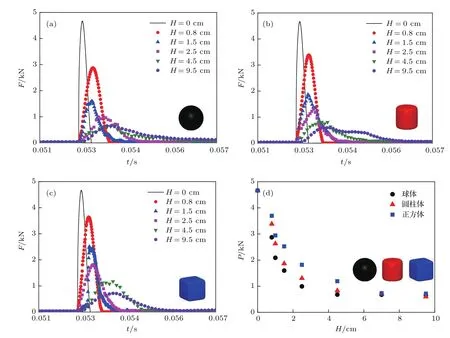
图10 不同颗粒层厚度下底板力的冲击力时程曲线 (a)球体;(b)圆柱体;(c)正方体;(d)三种形状的冲击力峰值变化Fig.10.Impact loads on bottom plate versus time under various thicknesses of granular with different shapes:(a)Sphere;(b)cylinder;(c)cube;(d)comparison of impact load peaks among three particle shapes.

4.2 不同颗粒尖锐度下密集度对冲击力的影响

为研究颗粒表面尖锐度对颗粒材料缓冲性能的影响,这里保证不同形态的单个颗粒质量相等,从而获得不同颗粒形状影响下的缓冲性能.由于超二次曲面方程产生的颗粒形状具有几何对称性,这里给出1/4的颗粒表面轮廓随函数尖锐度参数从2.0到8.0的变化过程,如图11(a)所示.通过表面尖锐度参数的连续变化实现颗粒形状从球体到正方体和圆柱体到正方体的两种形态转变,如图11(b)所示.可以发现,从球体到正方体变化的过程中保持参数n1=n2,而圆柱体到正方体变化的过程中保持参数n1=8.通过改变参数n2,从而得到在参数n2从2到8变化过程中13种具有不同表面尖锐度的颗粒形态.

图11 不同颗粒表面尖锐度参数对颗粒形状的影响Fig.11.In fluences of blockiness parameters on the particle shapes.

图12为从球体和圆柱体到正方体的两种形状变化过程中表面尖锐度参数分别为2.0,3.0,5.0,8.0时底板所受的冲击力时程.在两种形状变化过程中,对不同尖锐度下冲击力峰值p和颗粒系统初始密集度C0进行统计,如图13所示.可以发现,冲击力峰值和初始密集度随表面尖锐度的增加而显著增加.在颗粒随机堆积和冲击过程中,表面尖锐度的主要作用是将颗粒间的点接触逐步转变为面接触,增加颗粒间的接触面积,同时产生更加稳定且密实的颗粒系统.此外,增加颗粒表面尖锐度能阻止颗粒间的相对滑动和滚动,使冲击物在颗粒材料中的运行距离相对减小,从而产生较高的底部冲击力.以上结果表明:相比具有尖锐顶点和平面的颗粒形态,光滑表面的球形颗粒具有更好的缓冲效果.同时,颗粒间的面接触会提高颗粒系统的密实度,从而降低系统的缓冲性能.

4.3 不同颗粒长宽比下密集度对冲击力的影响

为进一步研究颗粒长宽比对缓冲特性的影响,通过改变超二次曲面方程得到不同的长宽比σ=c/a(=b),分别取σ=0.4,0.6,0.8,1.0,1.5,2.0,2.5和3.0得到8种不同长宽比的圆柱形和正方形颗粒形状,如图14所示.

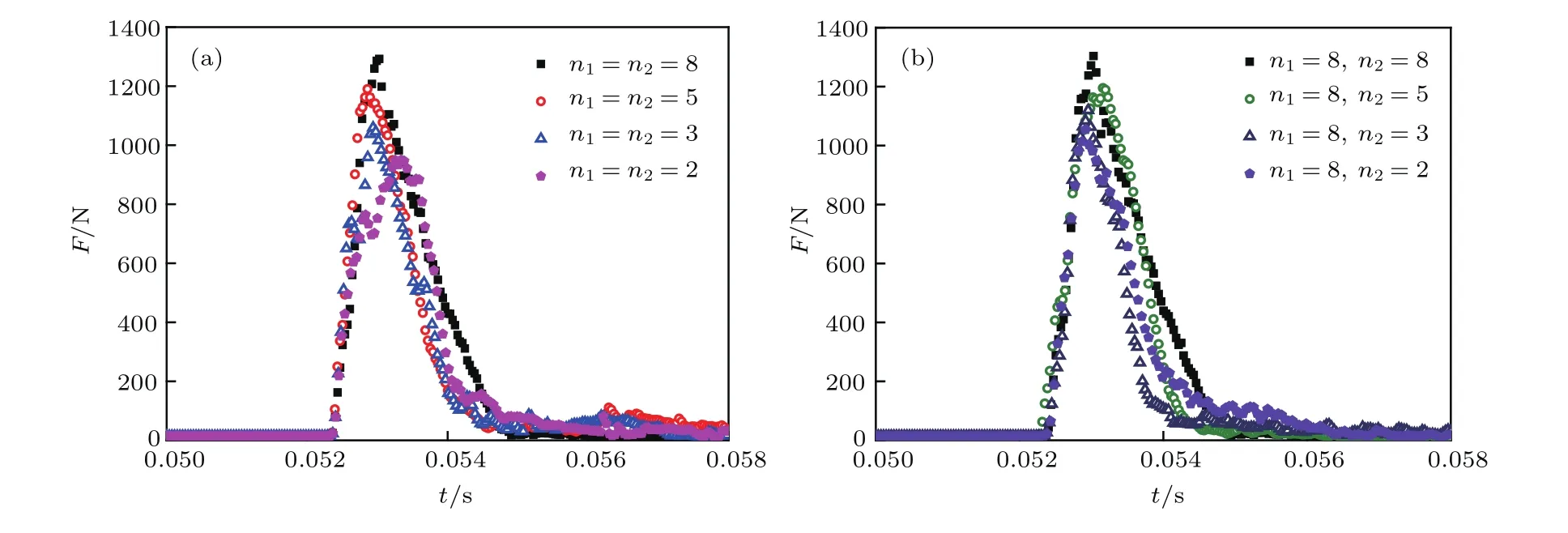
图12 不同形状变化过程中表面尖锐度对冲击力时程的影响 (a)球体-正方体;(b)圆柱体-正方体Fig.12.In fluences of blockiness parameters on the impact load versus time for the different changing processes:(a)Sphere-cube;(b)cylinder-cube.

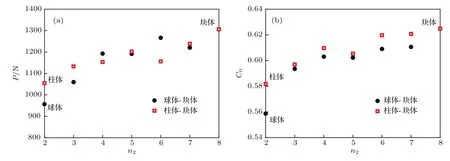
图13 不同表面尖锐度下冲击力峰值和初始密集度的变化 (a)冲击力峰值;(b)初始密集度Fig.13.Impact load peaks and initial granular concentration under various blockiness parameters:(a)Impact load peaks;(b)initial concentration of granular material.

图14 不同长宽比的圆柱形和长方形颗粒 (a)圆柱形颗粒;(b)长方形颗粒Fig.14.Cylinder-like particles and cube-like particles with various aspect ratios:(a)Cylinder-like particles;(b)cubelike particles.

图15为圆柱形和长方形颗粒的长宽比σ分别为0.4,1.0,1.5和2.5时底板的冲击力时程曲线.同时,分别对两种形状不同长宽比的冲击力峰值和初始密集度进行统计,如图16所示.可以发现,增加或减小长宽比会使底部冲击力峰值和颗粒系统的初始密集度降低,从而提高颗粒材料的缓冲性能.同时,对于相同长宽比的颗粒形态,长方形颗粒的底部冲击力峰值都高于圆柱形颗粒.这主要是由于长方形颗粒间的主要接触模式为面接触,从而产生更加密实且相对稳定的颗粒系统,缩短了冲击的持续时间,使得长方形颗粒具有较弱的缓冲性能.

在冲击过程中,颗粒长宽比的主要作用是调整紧密排列的颗粒系统,使颗粒间存在更多孔隙,颗粒在冲击载荷作用下有很大的自由移动空间.同时,颗粒长宽比降低了系统的稳定性,增加颗粒间的相对滑动和转动,延长冲击时间.此外,对于较高或较低长宽比的颗粒系统,颗粒间的自锁可以调整冲击力的传输方向并实现分散响应,从而将局部冲击力在空间进行扩展,具有较好的缓冲效果.

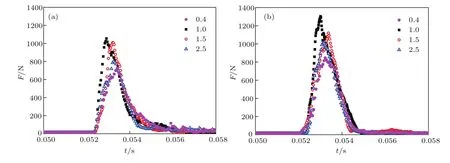
图15 不同圆柱形颗粒和长方形颗粒长宽比对冲击力时程的影响 (a)圆柱形颗粒;(b)长方形颗粒Fig.15.In fluences of aspect ratios on the impact load versus time for the different shapes:(a)Cylinder-like particles;(b)cube-like particles.

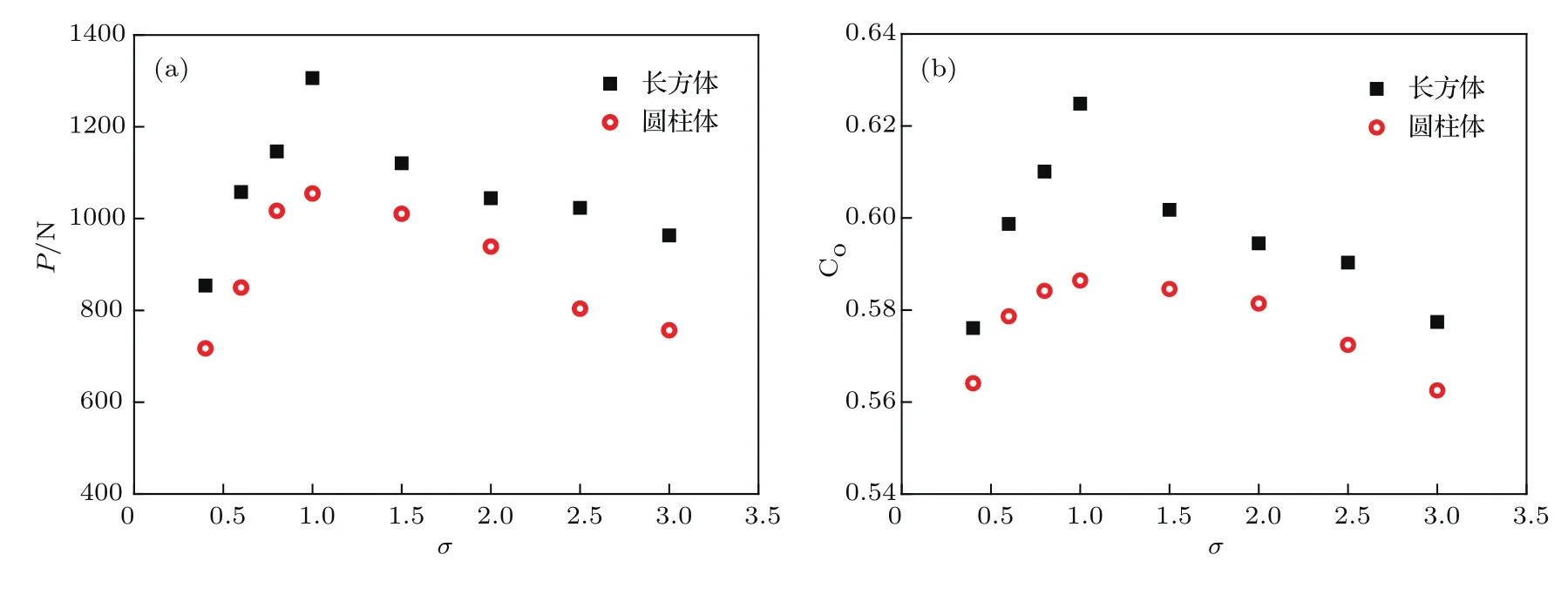
图16 不同长宽比下冲击力峰值和初始密集度的变化 (a)冲击力峰值;(b)初始密集度Fig.16.Impact load peaks and initial granular concentration under various aspect ratios:(a)Impact load peaks;(b)initial concentration of granular material.

5 结 语

基于超二次曲面方程构造非球形颗粒形态,在传统非线性接触模型的基础上考虑局部接触点处的平均曲率,采用离散元方法对颗粒材料在球形冲击物作用下的缓冲特性进行了数值分析.通过与圆柱体冲击的理论结果和球体冲击的实验结果进行对比验证,表明基于超二次曲面模型的离散元方法适用于模拟非球形颗粒的冲击过程.在此基础之上,进一步研究了颗粒层厚度、颗粒表面尖锐度和长宽比对底部冲击力的影响.研究结果表明:颗粒层厚度是影响不同形态颗粒材料缓冲特性的重要因素.当颗粒层厚度HHc时,缓冲性能对颗粒形状和颗粒层厚度不再敏感.同时,相比具有尖锐顶点和平面的颗粒形态,表面光滑的球形颗粒具有更好的缓冲效果.颗粒间的面接触会提高颗粒系统的初始密集度并增强系统的稳定性,从而降低颗粒材料的缓冲性能.此外,增加或减小圆柱形和长方形颗粒的长宽比,有利于颗粒间的相对滑动或转动,同时对于较高或较低长宽比的颗粒形态,颗粒间的自锁都会提高系统的缓冲性能.

参考文献

[1]Katsuragi H,Durian D J 2007Nat.Phys.3 420

[2]Kondic L,Fang X,Losert W,O’Hern C S,Behringer R P 2012Phys.Rev.E85 011305

[3]Nordstrom K,Lim E,Harrington M,Losert W 2014Phys.Rev.Lett.112 228002

[4]Bester C S,Behringer R P 2017Phys.Rev.E95 032906

[5]Seguin A,Bertho Y,Gondret P,Crassous J 2009Europhys.Lett.88 44002

[6]Clark A H,Petersen A J,Kondic L,Behringer R P 2015Phys.Rev.Lett.114 144502

[7]Deboeuf S,Gondret P,Rabaud M 2008Environ.Sci.Technol.42 8459

[8]Deboeuf S,Gondret P,Rabaud M 2009Phys.Rev.E79 041306

[9]Ye X Y,Wang D M,Zheng X J 2012Phys.Rev.E86 061304

[10]Lu G,Third J R,Müller C R 2015Chem.Eng.Sci.127 425

[11]Zhong W,Yu A,Liu X,Tong Z,Zhang H 2016Powder Technol.302 108

[12]Zhu H P,Zhou Z Y,Yang R Y,Yu A B 2007Chem.Eng.Sci.62 3378

[13]Zhu H P,Zhou Z Y,Yang R Y,Yu A B 2008Chem.Eng.Sci.63 5728

[14]Elskamp F,Kruggel-Emden H,Hennig M,Teipel U 2017Granular Matter19 46

[15]Zhao S,Zhang N,Zhou X,Zhang L 2017Powder Technol.310 175

[16]Kruggel-Emden H,Rickelt S,Wirtz S,Scherer V 2008Powder Technol.188 153

[17]Li C Q,Xu W J,Meng Q S 2015Powder Technol.286 478

[18]Zeng Y,Jia F,Zhang Y,Meng X,Han Y,Wang H 2017Powder Technol.313 112

[19]Galindo-Torres S A,Pedroso D M 2010Phys.Rev.E81 061303

[20]Toson P,Khinast J G 2017Powder Technol.313 353

[21]Govender N,Wilke D N,Pizette P,Abriak N E 2018Appl.Math.Comput.319 318

[22]Lu G,Third J R,Müller C R 2012Chem.Eng.Sci.78 226

[23]Cui Z Q,Chen Y C,Zhao Y Z,Hua Z L,Liu X,Zhou C L 2013Chin.J.Computat.Mech.30 854(in Chinese)[崔泽群,陈友川,赵永志,花争立,刘骁,周池楼 2013计算力学学报30 854]

[24]Cleary P W,Sinnott M D,Morrison R D,Cummins S,Delaney G W 2017Miner.Eng.100 49

[25]Di Renzo A,Di Maio F P 2004Chem.Eng.Sci.59 525

[26]Liu S D,Zhou Z Y,Zou R P,Pinson D,Yu A B 2014Powder Technol.253 70

[27]Goldman D I,Umbanhowar P 2008Phys.Rev.E77 021308

[28]Vet S J D,Bruyn J R D 2012Granular Matter14 661

[29]Clark A H,Petersen A J,Behringer R P 2014Phys.Rev.E89 012201

[30]Clark A H,Kondic L,Behringer R P 2016Phys.Rev.E93 050901

[31]Ji S Y,Li P F,Chen X D 2012Acta Phys.Sin.61 184703(in Chinese)[季顺迎,李鹏飞,陈晓东2012物理学报61 184703]

[32]Ji S Y,Fan L F,Liang S M 2016Acta Phys.Sin.65 104501(in Chinese)[季顺迎,樊利芳,梁绍敏2016物理学报65 104501]

[33]Sun Q C,Wang G Q 2008Acta Phys.Sin.57 4667(in Chinese)[孙其诚,王光谦 2008物理学报 57 4667]

[34]Peng Z,Jiang Y M,Liu R,Hou M Y 2013Acta Phys.Sin.62 024502(in Chinese)[彭政,蒋亦民,刘锐,厚美瑛2013物理学报62 024502]

[35]Barr A H 1981IEEE Comput.Graph.Appl.1 11

[36]Stenzel O,Salzer M,Schmidt V,Cleary P W,Delaney G W 2014Granular Matter16 457

[37]Delaney G W,Cleary P W 2010Europhys.Lett.89 34002

[38]Portal R,Dias J,de Sousa L 2010Arch.Mech.Eng.57 165

[39]Wellmann C,Lillie C,Wriggers P 2008Eng.Computat.25 432

[40]Podlozhnyuk A,Pirker S,Kloss C 2017Comp.Part.Mech.4 101

[41]Goldman R 2005Comput.Aided Geomet.Desig.22 632

[42]Gan J Q,Zhou Z Y,Yu A B 2017Powder Technol.320 610

[43]Kremmer M,Favier J F 2001Int.J.Numer.Meth.Eng.51 1407

[44]Kodam M,Bharadwaj R,Curtis J,Hancock B,Wassgren C 2010Chem.Eng.Sci.65 5863