经典瑞利-泰勒不稳定性界面变形演化的改进型薄层模型∗

赵凯歌 薛创 王立锋3) 叶文华3) 吴俊峰 丁永坤3) 张维岩3) 贺贤土3)

1)(中国工程物理研究院研究生院,北京 100088)

2)(北京应用物理与计算数学研究所,北京 100094)

3)(北京大学应用物理与技术研究中心,高能量密度物理数值模拟教育部重点实验室,北京 100871)

1 引 言

当两层流体的界面两侧具有连续的法向速度与压力,而其他物理量(如:密度、内能)不连续时,称为接触间断[1].在有势力场中流体密度梯度与压力梯度不平行时,那么接触间断面上的扰动幅度将被激发并增长,称为瑞利-泰勒不稳定性(Rayleigh-Taylor instability,RTI)[2−4].RTI是惯性约束聚变(inertial con finement fusion,ICF)研究的重要问题之一[5−8],也是许多天体物理现象的重要过程[9−11],例如:超新星爆炸和星系演化、天体射流等现象[12].在ICF的内爆加速和减速阶段中均引起RTI,RTI的发展影响点火热斑的形成、聚变燃烧和能量增益[13−22].超新星爆炸与ICF在动力学上十分相似,存在加速度引起的RTI.因此,研究RTI的物理机理对于天体物理中各类不稳定流动的演化具有十分重要的意义[12,23].

通过对界面不稳定性的理论研究[13−16,24−28]、数值模拟[17,18,29,30]及实验分析[31−34],将RTI的演化过程划分为线性阶段、变形阶段、规则非线性、不规则非线性及湍流混合阶段.理论研究方法大致分两类.一类是采用速度势及界面函数的微扰展开方法分析RTI的线性和弱非线性阶段[4,35,36].在线性阶段,理论分析与数值模拟和实验结果符合得很好[4,24,28,31].Jacobs和Catton[31]提出真空和流体界面(Atwood数等于1)的弱非线性(weakly non-linear,WNL)模型;Wang等[13,35,36]将WNL模型推广适用于任意Atwood数的情况,很好地描述了弱非线性阶段气泡和尖钉的产生过程.由于高次谐波的激发,导致小扰动展至高阶时将面对繁琐的计算.另一类是研究非线性阶段的气泡模型[37−43];Layzer[38]提出了对于真空和流体界面情况在气泡顶点附近采用势流理论的模型,描述了气泡在整个扰动过程中的发展行为.基于Layzer模型,Zhang[39]对任意时刻气泡和尖钉的运动规律进行了研究,Goncharov[40]和Sohn[41]将Layzer模型推广应用于任意Atwood数下的速度势模型.对于气泡和尖钉的大尺度相干运动,Abarzhi等[42]找到了多重调和解.Mikaelian[43]给定初始幅值,可以描述任意Atwood数的界面幅值关系式.陶烨晟等[44]将Layzer的气泡模型推广,描述了气泡由初始线性阶段到气泡以渐近速度增长的非线性阶段的发展过程.然而,Layzer模型仅能描述气泡和尖钉的顶点在扰动演变过程中的运动.

1972年,Ott[45]首先提出非线性RTI的薄层理论,通过分析薄层质点的受力,解释气泡和尖钉的形成过程[46,47].然而,Ott理论忽略了薄层两侧流体的分布.此外,当演变时间超过时,在波谷处出现界面卷曲现象,这里k=2π/λ表示波数,λ代表扰动波长,η0是界面扰动的初始幅值,g为重力加速度.Wang等[48]采用WNL模型对具有一定厚度的流体薄层中的RTI进行研究,详细分析薄层上下界面分别具有初始扰动状态时的演变规律.研究发现薄层厚度在扰动演变过程中起重要的作用.然而,在实际的流体不稳定性中,界面两侧的流体分布范围比较宽,近似经典RTI,而发生于界面附近的扰动按扰动波长成e指数形式衰减.当流体层厚度大于数倍的扰动波长时,在边界处的扰动已经衰减得非常小,因此,边界位置对界面处的扰动造成的影响可以忽略不计.本文将Ott的薄层模型应用于经典RTI界面变形演化过程.

本文在第2部分分析薄层模型的理论分析,给出界面的运动方程组;在第3部分首先数值求解运动方程组,其次分析薄层模型在RTI中的线性和弱非线性段的增长规律,再将模型的界面形变与数值模拟结果进行对比,最后将薄层模型扩展应用于分析扰动分布呈三角波和方波的情形;第4部分为本文的总结.

2 薄层RTI的理论模型

理想二维流体处于重力场(−gey)中,在接触间断的界面两侧为有限厚度层流体,其上下两层的流体密度分别为ρ2和ρ1(ρ2>ρ1).在界面附近选择一定厚度(h0)的流体薄层,平衡状态时,界面处的压强用p0表示,如图1(a).已知在重力场中压力近似由静压条件表述,其中p0表示平衡状态初始位置处的压强.当薄层受到扰动后,尖钉处压力增大,气泡处压力减小,流体薄层上下端面的压强分别用p2,p1表示,如图1(b).

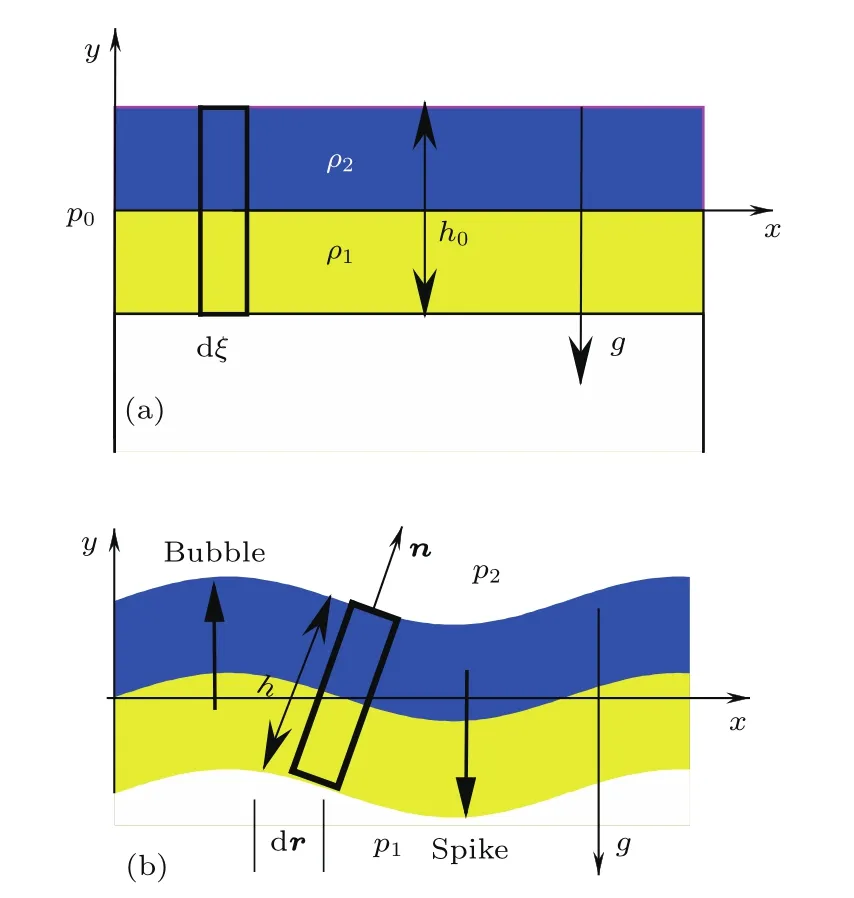
图1 流体薄层不稳定性的示意图 (a)平衡状态;(b)扰动状态Fig.1.The RTI of the thin layer:(a)Planar interface in equilibrium;(b)perturbed interface.

平衡状态时,选取流体薄层中的一点x=ξ,y=0,ξ是拉格朗日坐标;在t时刻,该点位于r(ξ,t)=x(ξ,t)ex+y(ξ,t)ey.考虑 平衡状态时另一点x=ξ+dξ,y=0,该点在t时刻位于r+(∂r/∂ξ)dξ处.研究分析ξ和ξ+dξ之间流体微团的运动规律,则流体微团的质量dm=(ρ1+ρ2)h0dξ/2=(ρ1+ρ2)h|dr|/2,其中h和|dr|表示扰动过程中流体微团的厚度和宽度.假设微团端面的压强不受扰动的影响,则上端面和下端面的压强分别为p2=p0−ρ2g(y+hey·n/2)和p1=p0−ρ1g(y−hey·n/2),如图1(b),则流体微团的受力关系:

其中,法向量则ey·方程(1)中−gdmey表示流体微团在重力场中的力,(p1−p2)|dr|n表示流场的压力场作用.由于微团的受力项满足dF=dm∂2r/∂t2,则运动方程的分量形式:

AT=(ρ1−ρ2)/(ρ1+ρ2)称为Atwood数,h0表示界面两侧流体层的初始厚度.方程(2)描述了流体界面RTI的形变规律,即形变的扰动范围由线性阶段到非线性阶段的演化过程.

在扰动初始阶段,x和y方向的位置坐标x(ξ,t)=ξ+ δx(ξ,t)和y(ξ,t)=δy(ξ,t), 其中δx(ξ,t)和δy(ξ,t)表示扰动小量.将位置坐标代入方程(2)中保留一阶小量,则y方向的扰动演化关系表示为

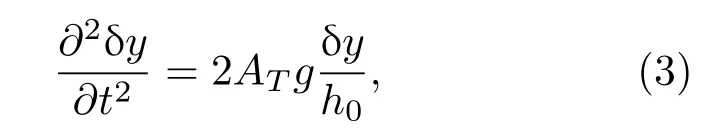
考虑扰动随时间呈exp(γt)形式,则增长率γ=

3 结果与讨论

3.1 数值计算方法

方程组(2)为非线性方程组,直接求解比较困难.因此,对方程组采用数值求解,将时间导数和空间导数分别采用隐式中心差分格式,∆t和∆ξ分别表示时间步长和空间步长.差分后的形式为

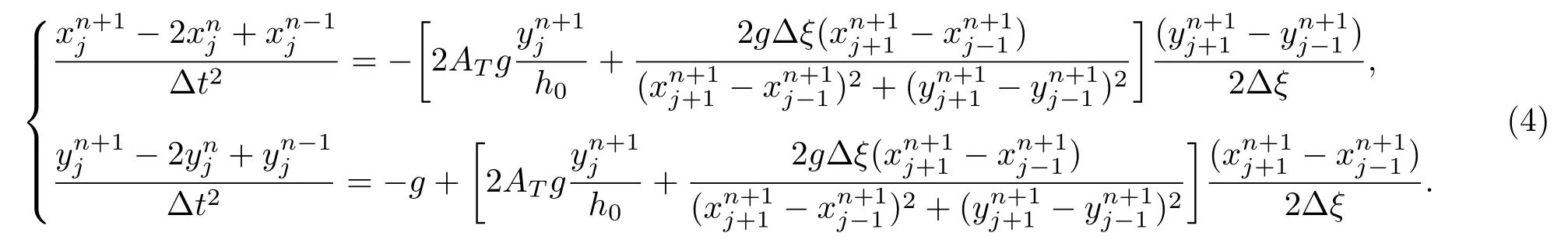
则方程组(4)差分后简为写如下的方程组:

式中,A表示系数矩阵,表示未知量矩阵,B为常数矩阵.上角标n和下角标j分别表示时间变量和空间变量.给定初始状态,采用Picard迭代求解方程组的结果.

3.2 线性及弱非线性阶段

首先,选择初始扰动的形式y=η0cos(kx),其中η0为初始扰动振幅,k=2π/λ为波数,λ为扰动波长.固定初始扰动幅值η0=0.02µm和加速度g=1µm/ns2,选择不同的薄层厚度h0,分析薄层模型的线性增长率关于Atwood数AT和波数k的变化关系,如图2所示.已知经典RTI在线性段的幅值增长称为线性增长率.

在薄层模型中分别选择薄层厚度kh0=1,2,4的情况分析界面不稳定性的演变规律,如图2所示,将薄层模型的线性增长率与经典RTI的结果进行比较.首先,在图2(a)中固定界面扰动的波长λ=1µm,对比薄层模型和经典RTI的线性增长率随AT数的变化规律.其次,在图2(b)中保持AT=0.6不变,对比薄层模型和经典RTI的线性增长率随扰动波数k的变化规律.通过图2(a)和图2(b)可以看出,薄层模型的线性增长率依赖于薄层厚度,已知界面处的扰动随距离界面的宽度呈指数衰减.当薄层厚度比较薄(kh0=1)时,薄层模型的线性增长率明显大于经典RTI的结果,导致薄层的界面演化加快,扰动增长趋于强烈;当薄层厚度比较厚(kh0=4)时,薄层模型的线性增长率明显小于经典RTI的结果,以致界面演化缓慢,扰动增长趋于舒缓;当且仅当薄层厚度满足条件kh0=2时,薄层模型的线性增长率随AT和k的变化规律与经典RTI的结果保持一致.因此,采用薄层模型描述界面的扰动发展规律时,应选择适当的薄层厚度与经典RTI的结果做比较.这与线性化分析的结果一致,在方程(3)中给出的增长率形式当薄层厚度满足h0=2/k时,增长率与经典RTI结果一致.

图2 选取不同的薄层厚度,比较薄层理论和经典RTI的线性增长率 (a)增长率关于AT数的关系;(b)增长率关于波数k的关系Fig.2.Comparision between linear growth rates obtained by the thin layer model and classical RTI at different thin layer thicknesses:(a)The function relation between the linear growth rate and the Atwood number;(b)the function relation between the linear growth rate and the wavenumber.

通过对比线性阶段的增长特征,可知在合适的薄层厚度(如h0=2/k)下,可以将模型的界面幅值与WNL模型做比较.已知三阶WNL模型给出关于RTI的弱非线性阶段界面为

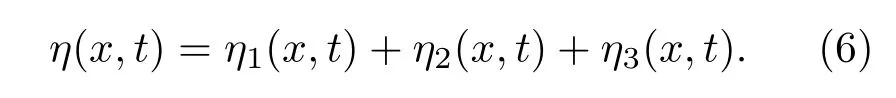
这里η1(x,t),η2(x,t)和η3(x,t)分别表示基模、二次谐波和三次谐波界面,其形式如下:

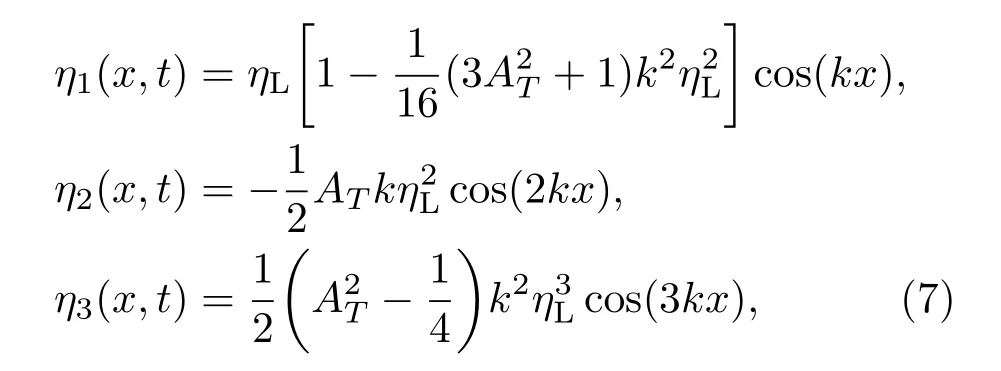
式中ηL=η0cosh(γct)代表基模的线性增长幅值,η0表示扰动的初始幅值,表示经典RTI的线性增长率.

选取初始扰动幅值η0=0.02µm和加速度g=1µm/ns2,分别选择三组不同的Atwood数和扰动波数,将薄层模型的界面幅值之和ηb+s=ηb+ηs与WNL模型做对比,如图3所示,这里ηb,ηs分别表示气泡和尖钉的幅值.图3(a)中,固定波长λ=5µm,选取AT=0.1,0.4,0.9;图3(b)中,固定AT=0.8,选取k=0.1,0.2,0.4.

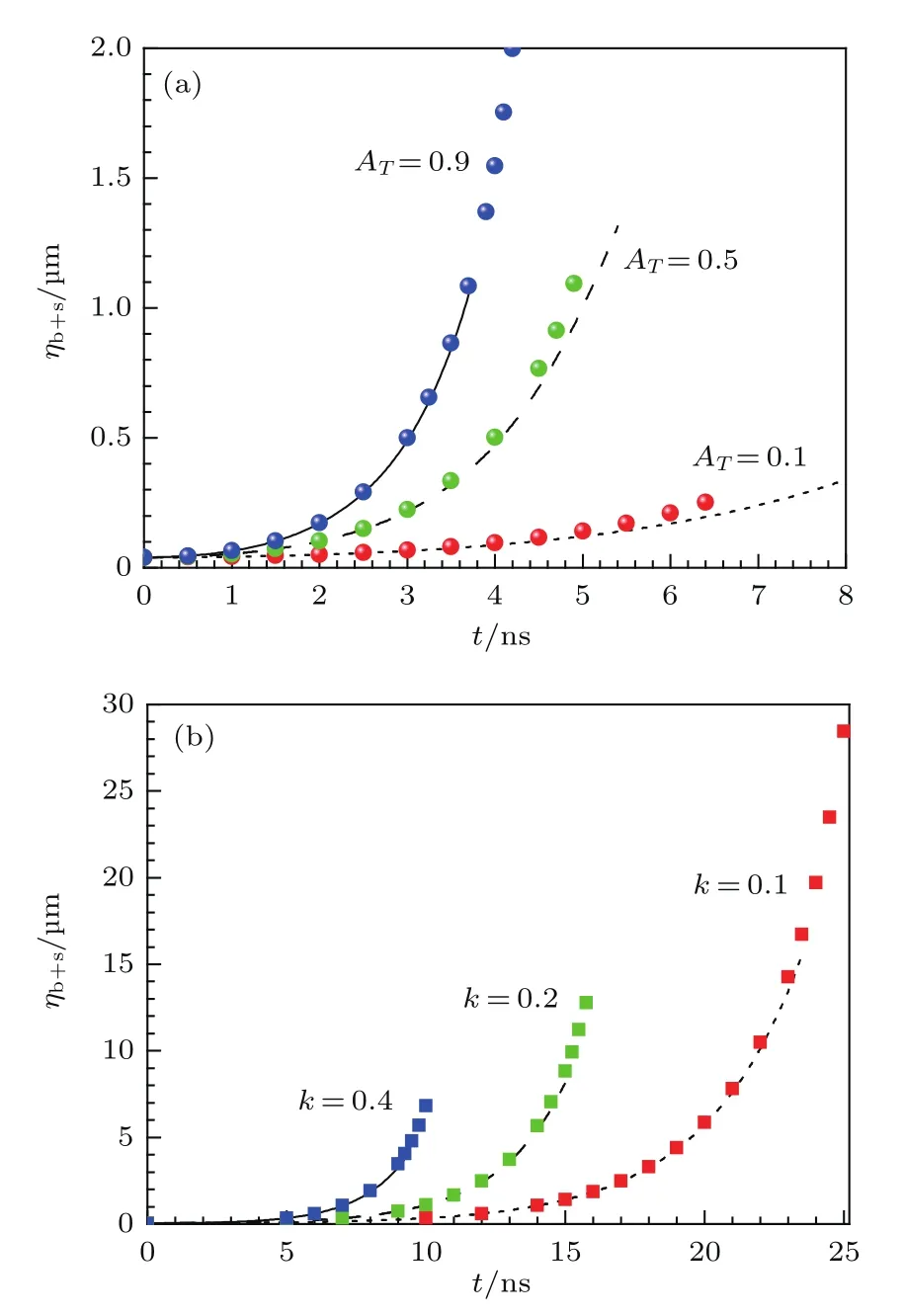
图3 固定η0=0.02µm和g=1µm/ns2,比较薄层模型和WNL模型的幅值关系 (a)波长λ=5µm,选取AT=0.1,0.5和0.9;(b)AT=0.8,选取k=0.1,0.2和0.4Fig.3.Comparision between the amplitudes obtained by the thin layer model and WNL model for RTI with fixed η0=0.02 µm and g=1 µm/ns2:(a)Choosing AT=0.1,0.5,and 0.9 with the wavelength λ=5 µm;(b)choosing k=0.1,0.2,and 0.4 with the Atwood number AT=0.8.

在图3中,将薄层模型的幅值之和与WNL模型的结果做比较,图3(a)中选取不同的AT数,图中曲线和圆点分别代表WNL模型和薄层模型的结果;图3(b)中选取不同的波数k,图中曲线和方块分别代表WNL模型和薄层模型的结果.可以看出,薄层模型与WNL模型在线性段及弱非线性区域内符合得相当好,说明薄层模型可以准确描述不稳定性的弱非线性段.然而,二者也存在一定的差别.在图3(a)中,当AT数比较小(AT=0.1)时,薄层模型仅能够描述初始线性段的扰动,薄层模型描述至t=6.4 ns时刻,随后的扰动演变规律不能准确给出,这是由于AT比较小,数值计算中导致误差较大;当AT数比较大(例如AT=0.9)时,WNL模型可以准确描述至幅值ηb+s=1.1µm的情况,而薄层模型的描述范围远大于WNL模型.在图3(b)可明显看出,薄层模型在描述不稳定性的演变规律时其适用性大于WNL模型.

3.3 变形与非线性演化

为进一步说明薄层模型的理论,将界面的变形和非线性演化过程与数值模拟的结果做对比.在数值模拟中,其上下层的流体密度分别为扰动波长λ=20µm,初始压强p0=5 MPa,加速度g=17µm/ns2,气体绝热指数γh=5/3.在下面的模拟中,这些参数保持不变.

首先,对比不稳定性在线性阶段的界面分布规律.界面初始幅值η0=0.075µm,图4给出了不稳定性在线性阶段的分布,图4(a)—(d)和(a′)—(d′)分别表示薄层模型和数值模拟所描述的在不同时刻的不稳定性界面.通过对比发现,薄层模型在描述扰动演化的线性阶段,界面呈现规则的余弦形状;随扰动的演化,界面的波峰向上增长,波谷向下发展,发现薄层模型的不稳定界面与数值模拟的结果在线性阶段的界面增长基本一致.

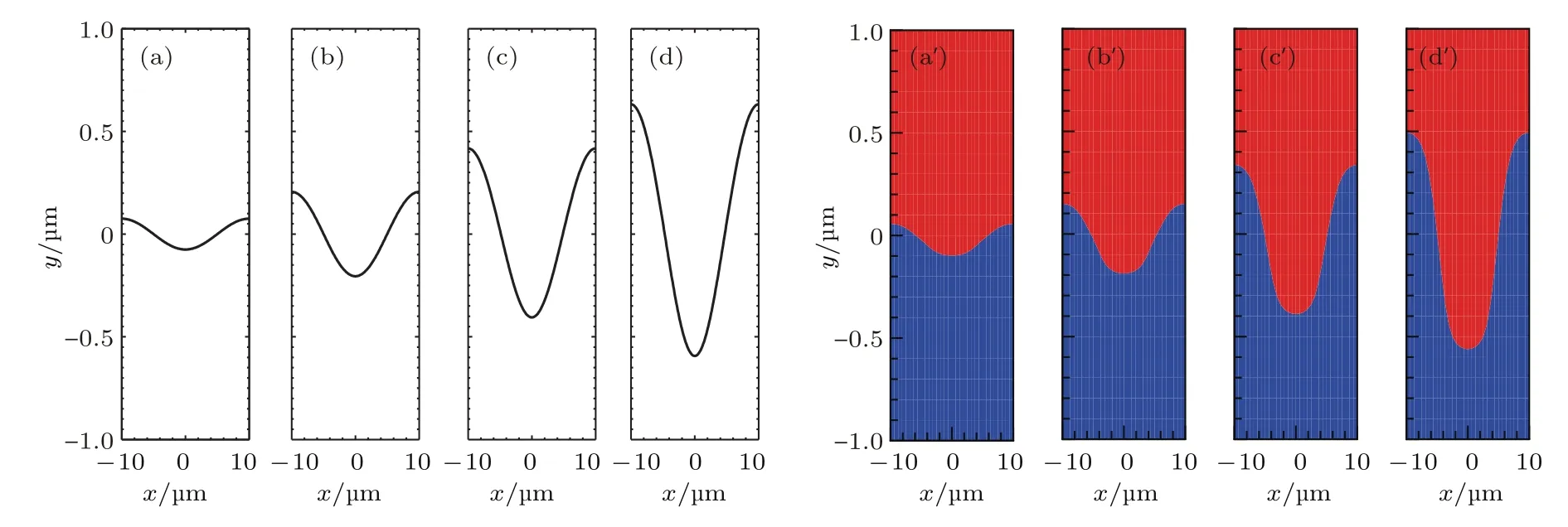
图4 (a)—(d)薄层模型和(a′)—(d′)数值模拟所描述的在线性阶段的不稳定界面 (a),(a′)t=0.0 ns;(b),(b′)t=0.4 ns;(c),(c′)t=0.8 ns;(d),(d′)t=1.0 nsFig.4.Perturbed interfaces obtained by the(a)–(d)thin layer model and(a′)–(d′)numerical simulation in the linear stage:(a),(a′)t=0.0 ns;(b),(b′)t=0.4 ns;(c),(c′)t=0.8 ns;(d),(d′)t=1.0 ns.

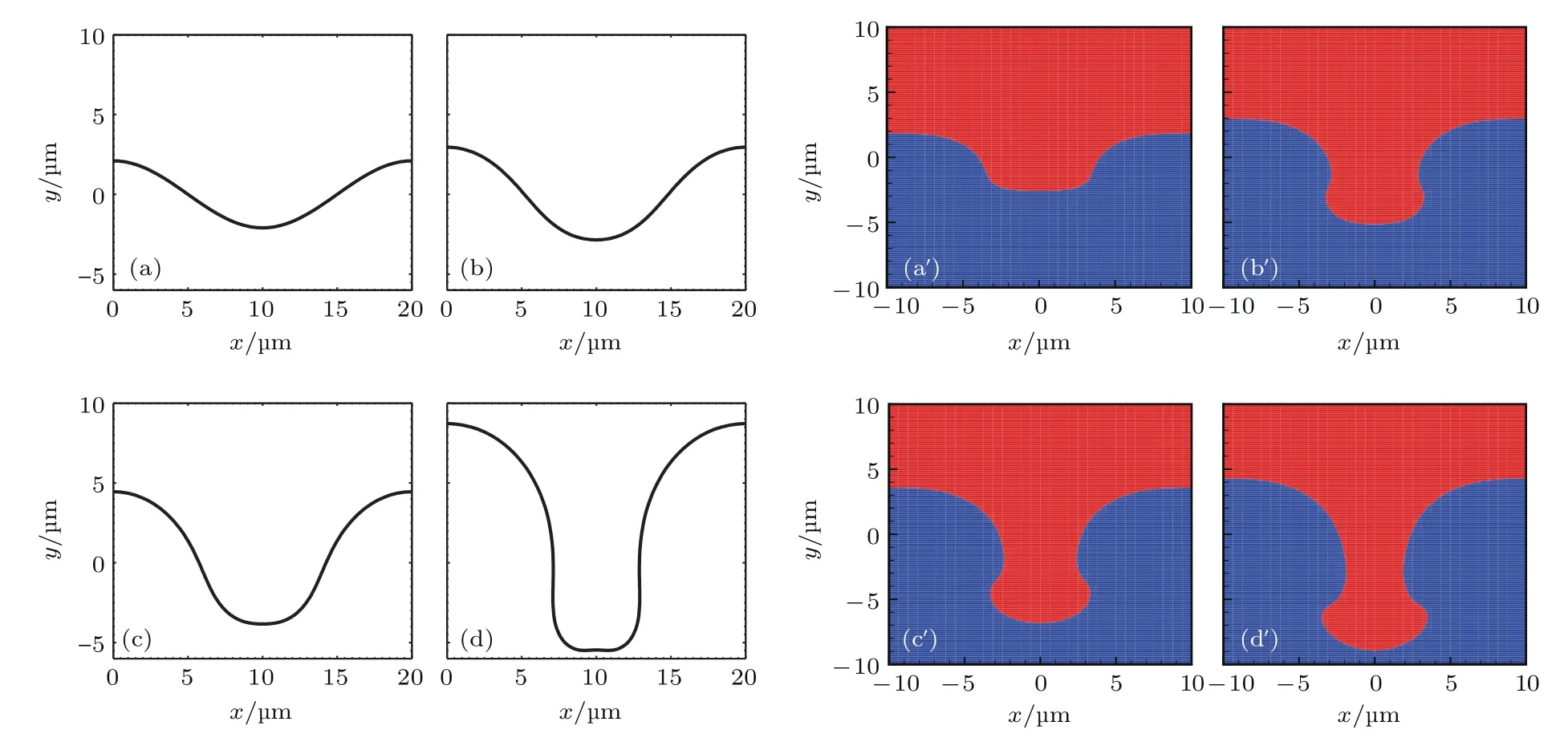
图5 (a)—(d)薄层模型和(a′)—(d′)数值模拟所描述的在非线性阶段的不稳定界面 (a),(a′)t=0.0 ns;(b),(b′)t=0.4 ns;(c),(c′)t=0.6 ns;(d),(d′)t=0.82 nsFig.5.Perturbed interfaces obtained by the(a)–(d)thin layer model and(a′)–(d′)numerical simulation in the nonlinear stage:(a),(a′)t=0.0 ns;(b),(b′)t=0.4 ns;(c),(c′)t=0.6 ns;(d),(d′)t=0.82 ns.

其次,对比不稳定性在非线性阶段的界面分布规律.假设界面的初始扰动幅值η0=2.0µm,图5(a)—(d)和(a′)—(d′)分别表示薄层模型和数值模拟所描述的非线性阶段的不稳定性界面.通过对比,薄层模型与数值模拟在描述扰动发展中的界面幅值的总长度基本保持一致;然而,在薄层模型的发展后期,波峰幅值明显大于波谷幅值,这是由于薄层模型中微团上下端面的面积在整个演变过程中是相等的,导致波峰端面受压力比实际情况要小,波谷端面受力比实际要大,使得气泡增长加快,尖钉增长变缓,说明薄层模型可以用于描述初始为大扰动幅值的不稳定性.另外,薄层模型在扰动发展的后期(t=0.82 ns),波谷顶端出现类“蘑菇”形结构,可以解释非线性阶段“蘑菇”成型的原因.

3.4 扩展应用

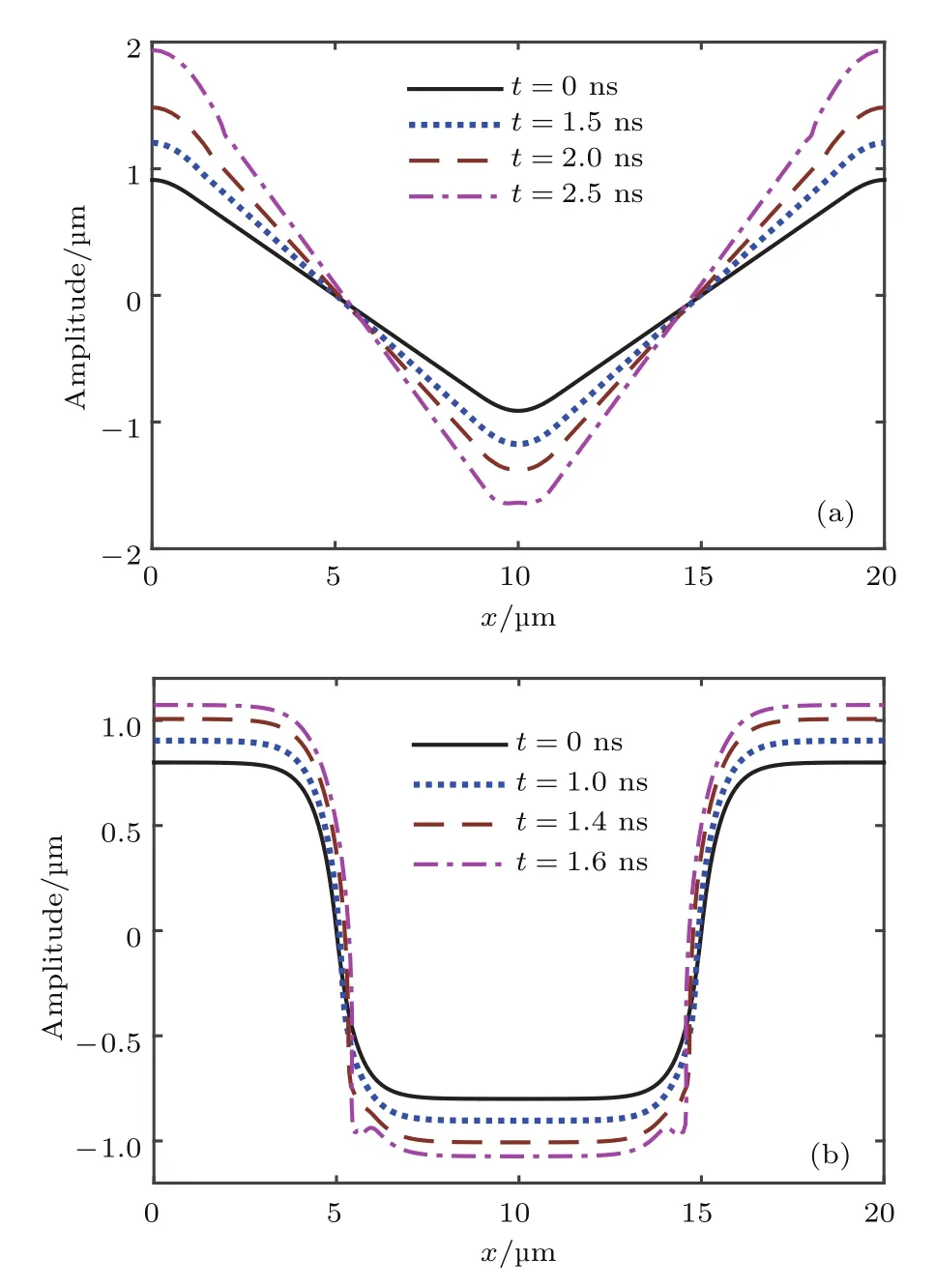
图6 薄层模型应用于任意初始波形的不稳定界面 (a)初始三角波分布;(b)初始方波分布Fig.6.Thin Layer model is applied to obtained the arbitrary perturbed distributions at the initial moment:(a)The perturbed interface with triangular wave;(b)the perturbed interface with square wave.

由于薄层模型是基于对流体微团的受力分析,因此,薄层模型不仅可以应用于初始小扰动的不稳定性,而且可以描述初始大扰动的情况.同时,可以描述任意初始波形的不稳定界面,例如三角波、方波等.

图6(a)和图6(b)分别展示了初始扰动界面为三角波和方波的界面演变分布,其中扰动波长λ=20µm,重力加速度g=1µm/ns2及Atwood数AT=0.8相同.如图6所示:在初始阶段三角波和方波的扰动界面均表现出规则的形变规律,波峰和波谷的增长幅度基本一致;随着扰动的发展,波峰的增长幅度稍大于波谷;针对三角波界面,在t=2.5 ns时刻,波谷的顶端处于水平状态,自此之后,薄层模型描述的波谷位置将会出现凸起现象,薄层模型已经不能准确描述扰动的发展;针对方波界面,在t=1.6 ns时刻,波谷处的界面出现不规则形变,这是由于薄层模型在描述不稳定性时,界面微元向波谷处聚集,导致微元之间相互碰撞.由于薄层模型是基于界面微元的受力分析,因此,初始时界面处于直线状态(例如:水平、斜线)时,扰动在演变过程中对此区域的界面不会带来形变影响,界面始终保持直线状态.

4 结 论

本文在Ott薄层理论的基础上,发展了能够描述任意Atwood数的薄层模型.该模型的数值解分别与WNL模型、数值模拟结果比较,薄层模型可以准确描述线性和弱非线性的界面演化和形状;在非线性阶段中“蘑菇”形状的发展过程中,界面形状比较接近数值模拟的结果.通过研究发现,薄层模型可以描述初始大扰动幅值的不稳定性.此外,对于初始时任意分布的扰动界面,该模型均可以很好地描述其演化过程.该模型可以推广至三维球形几何,有助于人们理解内爆过程中薄层界面的形变规律和演化机理.

参考文献

[1]Wang J H 1994Nonstationary Flow and Shock for Two-Dimensional(Beijing:Science Press)p10(in Chinese)[王继海 1994二维非定常流和激波 (北京:科学出版社)第10页]

[2]Rayleigh L 1893Proc.R.Math.Soc.14 170

[3]Taylor G I 1950Proc.R.Soc.London:Ser.A201 192

[4]Chandrasekhar S 1961Hydrodynamic and HydromagneticStability(London: Oxford University Press)pp429–514

[5]Nuckolls J H,Wood J,Thiessen A,Zimmerman G 1972Nature239 139

[6]Lindl J D,Amendt P,Berger R L,Glendinning S G,Glenzer S H,Haan S W,Kau ff man R L,Landen O L,Suter L J 2004Phys.Plasmas11 339

[7]Atzeni S,Meyer-ter-Vehn J 2004The physics of Inertial Fusion:Beam Plasma Interaction,Hydrodynamics,Hot Dense Matter(Oxford:Oxford University Press)

[8]He X T,Zhang W Y 2007Eur.Phys.J.D44 227

[9]Remington B A,Drake R P,Ryutov D D 2006Rev.Mod.Phys.78 755

[10]Remington B A,Arnett D,Drake R P,Takabe H 1999Science284 1488

[11]Committee on High Energy Density Plasma Physics Plasma Science Committee Board on Physics and Astronomy Division on Engineering and Physical Science 2001Frontiers in High Density Physics(Washington,DC:Academic Press)

[12]Vlemmings W H T,Diamond P J,Imai H 2006Nature440 58

[13]Wang L F,Ye W H,Li Y J 2010Phys.Plasmas17 052305

[14]Liu W H,Wang L F,Ye W H,He X T 2012Phys.Plasmas19 042705

[15]Wang L F,Wu J F,Fan Z F,Ye W H,He X T,Zhang W Y,Dai Z S,Gu J F,Xue C 2012Phys.Plasmas19 112706

[16]Wang L F,Ye W H,Sheng Z M,Don W S,Li Y J,He X T 2010Phys.Plasmas17 122706

[17]Ye W H,Wang L F,He X T 2010Phys.Plasmas17 122704

[18]Wang L F,Ye W H,He X T,Zhang W Y,Sheng Z M,Yu M Y 2012Phys.Plasmas19 100701

[19]Wang L F,Ye W H,Wu J F,Liu J,Zhang W Y,He X T 2016Phys.Plasmas23 052713

[20]Wang L F,Ye W H,Wu J F,Liu J,Zhang W Y,He X T 2016Phys.Plasmas23 122702

[21]Wang L F,Ye W H,He X T,Wu J F,Fan Z F,Xue C,Guo H Y,Miao W Y,Yuan Y T,Dong J Q,Jia G,Zhang J,Li Y J,Liu J,Wang M,Ding Y K,Zhang W Y 2017Sci.China:Phys.Mech.Astron.60 055201

[22]Zhang W Y,Ye W H,Wu J F,Miao W Y,Fan Z F,Wang L F,Gu J F,Dai Z S,Cao Z Y,Xu X W,Yuan Y T,Kang D G,Li Y S,Yu X J,Liu C L,Xue C,Zheng W D,Wang M,Pei W B,Zhu S P,Jiang S E,Liu S Y,Ding Y K,He X T 2014Sci.Sin.:Phys.Mech.Astron.44 1(in Chinese)[张维岩,叶文华,吴俊峰,缪文勇,范征锋,王立锋,谷建法,戴振生,曹柱荣,徐小文,袁永腾,康洞国,李永升,郁晓瑾,刘长礼,薛创,郑无敌,王敏,裴文兵,朱少平,江少恩,刘慎业,丁永坤,贺贤土 2014中国科学:物理学力学 天文学44 1]

[23]Reipurth B,Bally J 2001Annu.Rev.Astron.Astrophys.39 403

[24]Jacobs J W,Catton I 1988J.Fluid Mech.187 353

[25]Kull H J 1991Phys.Rep.206 197

[26]Sanz J 1994Phys.Rev.Lett.73 2700

[27]Garnier J,Raviart P A,Cher fils-Clérouin C,Masse L 2003Phys.Rev.Lett.90 185003

[28]Haan S W 1991Phys.Fluids B3 2349

[29]Youngs D L 1984Physica D12 32

[30]Zhang Y,Drake R P,Glimm J 2007Phys.Plasmas14 062703

[31]Jacobs J W,Catton I 1988J.Fluid Mech.187 329

[32]Waddell J T,Niederhaus C E,Jacobs J W 2001Phys.Fluids13 1263

[33]Wilkinson J P,Jacobs J W 2007Phys.Fluids19 124102

[34]Olson D H,Jacobs J W 2009Phys.Fluids21 034103

[35]Wang L F,Ye W H,Li Y J 2010Chin.Phys.Lett.27 025203

[36]Wang L F,Wu J F,Ye W H,Zhang W Y,He X T 2013Phys.Plasmas20 042708

[37]Davies R M,Taylor G I 1950Proc.Roy.Soc.A200 375

[38]Layzer D 1955Astrophys.J.122 1

[39]Zhang Q 1998Phys.Rev.Lett.81 3391

[40]Goncharov V N 2002Phys.Rev.Lett.88 134502

[41]Sohn S 2003Phys.Rev.E67 026301

[42]Abarzhi S I,Nishihara K,Glimm J 2003Phys.Lett.A317 470

[43]Mikaelian K O 2003Phys.Rev.E67 026319

[44]Tao Y S,Wang L F,Ye W H,Zhang G C,Zhang J C,Li Y J 2012Acta Phys.Sin.61 075207(in Chinese)[陶烨晟,王立锋,叶文华,张广财,张建成,李英骏 2012物理学报61 075207]

[45]Ott E 1972Phys.Rev.Lett.29 1429

[46]Manheimer W,Colombant D,Ott E 1984Phys.Fluids27 2164

[47]Colombant D,Manheimer W,Ott E 1984Phys.Rev.Lett.53 446

[48]Wang L F,Guo H Y,Wu J F,Ye W H,Liu J,Zhang W Y,He X T 2014Phys.Plasmas21 122710