铷原子D1线真空压缩光场的产生及态重构∗

李淑静 张娜娜 闫红梅 徐忠孝 王海

1)(山西大学光电研究所,量子光学与光量子器件国家重点实验室,太原 030006)

2)(山西大学,极端光学协同创新中心,太原 030006)

1 引 言

压缩态光场是一类重要的连续变量非经典光源,在精密测量[1−3]、量子信息处理[4,5]方面有广泛的应用.量子态存储是量子中继、远距离量子通信[6,7]的基础,而碱金属原子由于具有长的基态相干时间,是理想的量子态存储介质[8−12].随着原子介质中量子存储技术的快速发展,产生与碱金属原子共振的压缩态光场成为近年来量子信息领域的一个研究热点.

产生压缩态的方法主要有光学参量振荡[13−17],原子系综中的偏振自旋转[18−21]以及四波混频[22−24],其中光学参量振荡是最成熟和有效的方法.近年来,对于碱金属原子吸收波段压缩态光场产生方面的研究进展非常快.2006年,Tanimura等[25]在795 nm波段(铷原子D1线)产生了−2.75 dB的真空压缩;2007年,Takeno等[16]在860 nm波段(接近于铯原子D2线852 nm)得到了−9 dB的真空压缩;2007年,Hétet等[26]将795 nm波段的真空压缩度提高到−5.2 dB;2009年,Burks等[17]在852 nm波段(铯原子D2线)50 kHz边带处获得−3 dB的压缩;2016年,Han等[15]将795 nm波段的真空压缩度进一步提高到−5.6 dB.在上述报道中,大多只关注光场的压缩度,而没有对其进行态重构.所谓态重构就是利用量子层析术对量子态特征进行刻画,从中得到密度矩阵和相空间的Wigner函数,重现该量子态的全部信息.传统的用逆Randon变换方法进行量子层析[27−29],这种方法首先需要通过光场不同相位角下的噪声分布计算出边缘分布,然后才能得到相空间的Wigner准概率分布函数.近年来发展起来的极大似然估计法[30,31]在量子态层析过程中不仅可以绕开边缘分布,而且预先对密度矩阵进行了正定、厄米、归一化的限制,重构结果更符合物理实际.

本文采用周期极化磷酸氧钛(periodically poled KTiOPO4,PPKTP)晶体作为非线性介质,通过光学参量振荡过程产生了795 nm真空压缩光场.通过一束本振光构成平衡零拍测量系统对产生的压缩光场进行探测,在抽运功率45 mW时获得−3 dB的压缩和5.8 dB的反压缩.在示波器上对平衡零拍测量系统的时域信号进行采集,得到压缩态光场不同相位角下的噪声分布;然后利用极大似然估计法对压缩态光场进行重构,得到了密度矩阵及光子数分布,通过密度矩阵计算了相空间的Wigner函数.理论上我们计算了压缩真空态的光子数分布和Wigner函数,并对理论和实验重构结果进行了分析和比较.

2 795 nm真空压缩态的产生

795 nm真空压缩态光场产生的实验装置如图1所示.连续钛宝石激光器(M Square Lasers,SolsTis)输出的光波长为795 nm,对应于铷原子的吸收线.电光调制器对光场进行相位调制,用于对倍频腔和光学参量振荡腔(optical parametric oscillator,OPO)进行边带锁定[32].钛宝石激光器输出的大部分光进入倍频腔,对795 nm的光进行倍频,产生397.5 nm的紫光,作为OPO的抽运光.倍频腔为四镜环形腔,由两个凹面镜和两个平面镜组成,其中平面镜PT1的透过率为10%@795 nm,作为倍频腔的输入镜,其余腔镜均对795 nm的红外高反.两个凹面镜的曲率半径均为100 mm,晶体处的腰斑半径为20µm.选用一块10 mm长的I类PPKTP晶体用于倍频产生,注入200 mW的795 nm红外光可产生60 mW的397.5 nm紫光.OPO腔也是四镜环形腔,包含两个凹面镜和两个平面镜.平面镜PT2的透过率是10%@795 nm,用作OPO腔的输出镜,其余腔镜均对795 nm的光高反.OPO腔往返腔长480 mm,选用一块10 mm长的I类PPKTP晶体进行参量下转换.凹面镜的曲率半径是50 mm,晶体处的腰斑半径是10µm,估算OPO腔的阈值约为160 mW.

从钛宝石激光器输出的一部分光通过单模光纤后作为OPO腔的探针光、锁定光以及平衡零拍探测(balanced homodyne detector,BHD)的本振光.探针光从高反平面镜M1注入OPO腔,用来测量OPO腔的经典参量增益,探针光从OPO腔输出后进入探测器PD1进行探测.锁定光也从平面镜M1注入OPO腔,锁定光和探针光在腔内反向传播,锁定光从OPO腔输出后用探测器PD2探测,从测量信号提取误差信号对OPO腔锁定.本振光经过模清洁器后与OPO腔输出光场在50/50分束器上干涉,干涉信号进入一对光电探测器,构成BHD系统.

探测器的光电管选用Hamamatsu Photonics公司生产的S3883,量子效率为94%.两个探测器的信号之差作为BHD的输出,将产生的交流信号输入频谱分析仪对OPO输出光场的噪声进行测量.在抽运功率45 mW时,扫描本振光相位,测量了产生压缩光场的噪声曲线(图2曲线a),获得−3 dB的压缩和5.8 dB的反压缩,图2曲线b为散粒噪声基准,测量频率为2 MHz.

OPO输出光场的噪声方差可以表示为[25]

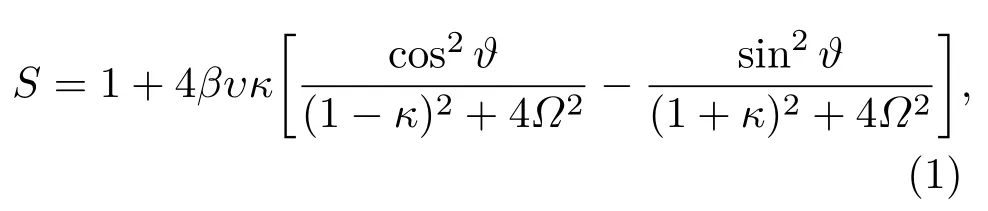
图1 实验装置图(Ti:sapphire,钛宝石激光器;EOM,电光调制器;SHG,二次谐波产生;OPO,光学参量振荡腔;MC,模清洁器;F,可翻转反射镜;HBS,50:50分束器;PD1,PD2,光电探测器;SMF,单模光纤;BHD,平衡零拍探测)Fig.1.Experimental setup(Ti:sapphire,Ti:sapphire laser;EOM,electro-optic modulator;SHG,second harmonic generation;OPO,optical parametric oscillator;MC,mode-cleaner cavity;F, flipper mirror;HBS,50:50 beam splitter;PD1,PD2,photo detectors;SMF,single-mode fiber;BHD,balanced homodyne detector).

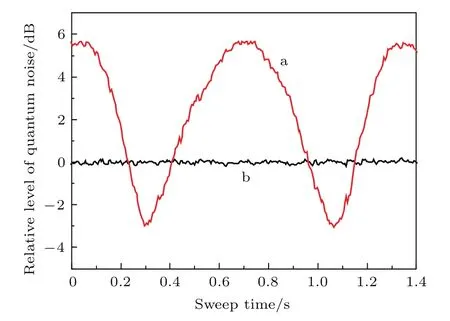
图2 (a)扫描本振光相位时,压缩态光场的噪声曲线;(b)散粒噪声基准;谱仪的测量频率2 MHz,分辨带宽100 kHz,视频带宽30 HzFig.2.(a)Measured quantum noise levels of squeezed light when the local oscillator beam phase is scanned;(b)shotnoise level.The settings of the spectrum analyzer are zerospan mode at 2 MHz,resolution bandwidth of 100 kHz,and video bandwidth of 30 Hz.

式中,ϑ为压缩光和本振光之间的相对相位;β=ης2ζ为总的探测效率,η是BHD的量子效率,ς是BHD系统中信号光和本振光的干涉对比度,ζ是光路传输效率,实验中η=0.94,ς=0.97,ζ=0.99,因此β=0.876;υ=T/(T+L)是OPO腔的逃逸效率,其中T是输出耦合镜的透过率,L是内腔损耗,实验中L=1.5%,υ=0.87;为归一化的抽运参数,Ppump为抽运功率,Pth为振荡阈值,G为参量增益,实验中45 mW抽运功率下,增益为4,对应的抽运参数κ=0.5;Ω=2πf/γ为失谐参数,f是测量频率,γ=c(T+L)/d是腔的衰减率,c是光速,d是往返腔长,实验中失谐参数Ω=0.2.利用(1)式,计算得到光场的压缩度和反压缩度分别为−4.34 dB和6.73 dB.压缩度和反压缩度的测量结果均小于理论计算值,原因主要是当397.5 nm紫光抽运OPO腔时,由于“灰迹”效应导致PPKTP晶体对红外的吸收增加[33],使OPO内腔损耗增加,逃逸效率降低.与文献[15,26]相比,在本文实验中内腔损耗(无抽运光时)偏大,主要因为PPKTP晶体通光面镀膜质量不高,通过改善晶体镀膜质量,压缩度可进一步提高.

3 利用极大似然估计重构量子态

极大似然估计是近年来发展起来的一种量子层析术,首先对光场做大量的投影测量,得到各投影基下的概率分布;然后建立似然函数,利用重复迭代计算出最可能的密度矩阵使测量结果出现的概率最大.与传统的逆拉登变换方法相比,极大似然估计可以更好地保持量子态的物理特性,而且在重构过程中可以绕开正交分量的边缘分布[30,31].我们利用极大似然估计重构了压缩态光场的密度矩阵,得到了光子数分布,并通过密度矩阵计算了相空间的Wigner函数.实验中,将BHD输出信号输入数字存储示波器,扫描本振光的相位,在时域上得到压缩光场不同相位角下的噪声分布.提取2 MHz频率处的信号进行处理,提取信号的原理图如图3所示.将平衡零拍信号与2 MHz射频进行混频,通过低通滤波,将目标信号搬移到低频.然后利用低噪声放大器对信号进行放大,在示波器上进行观察.示波器上测量到的时域噪声信号如图4所示,两条红虚线之间的数据对应的相位在0—π之间,利用这些数据重构密度矩阵.

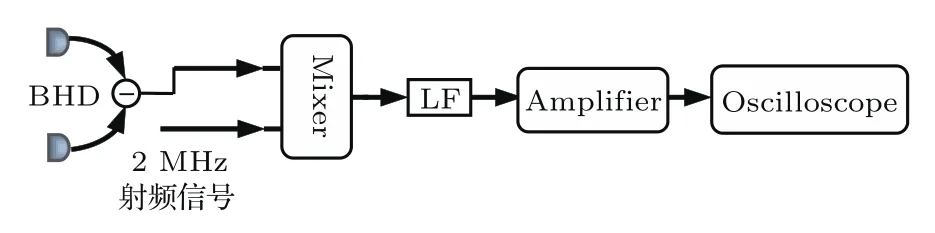
图3 提取2 MHz处平衡零拍探测信号示意图(Mixer,混频器;LF,低通滤波器;Ampli fier,低噪声放大器;Oscilloscope,数字存储示波器)Fig.3.Schematic diagram of extracting the signals of balanced homodyne detector at 2 MHz.Mixer,frequency mixer;LF,low-pass filter;Ampli fier,low noise ampli fier;Oscilloscope,digital storage oscilloscope.

图4 压缩态噪声的时域测量结果(两条虚线中间数据的相位范围为0—π)Fig.4.Noise of squeezed state measured in time domain(the phase range of the data between the two dashed lines is 0–π).

若量子态的密度矩阵为,在相位θ下对正交分量进行测量,正交分量x值出现的概率为:是投影算符.由于测量得到的正交分量值是连续的,不能直接做迭代算法,而首先需要将其离散化.离散化后每一份内最多只包含一个正交分量测量点,这种情况下,数据集{(θi,xi)}的似然函数为:通过迭代算法对密度矩阵进行计算,其中迭代函数随着迭代次数的增加似然函数值单调递增,计算得到的密度矩阵就越接近于制备态的真实密度矩阵.重构过程在光子数态基下进行,在计算中不能包含所有的数态,需要对数态基做截断处理,大于某个值的光子数态被排除在分析之外.在重构过程中,只考虑光子数为0—10的态.选择单位矩阵作为初始密度矩阵,重复迭代1000次,得到密度矩阵:

密度矩阵的对角元为光子数概率,图5给出了光子数概率的直方图(左列黑色).理想情况下由下转化过程产生的压缩态光场为偶光子数态,因为下转换光子总是成对产生.但是本文的实验重构结果中不仅有偶光子数态,还包含了奇光子数态,这主要来源于系统损耗和不完美的探测器量子效率.压缩态产生系统中的损耗和不完美体现在压缩度的测量结果上,就会使反压缩度的绝对值大于压缩度的绝对值,这与本文压缩度的测量结果相符.

为了将利用极大似然估计得到的态重构结果与理论计算结果进行比较,我们理论计算了真空压缩态的光子数分布和Wigner函数.单模真空压缩态的Wely特征函数为

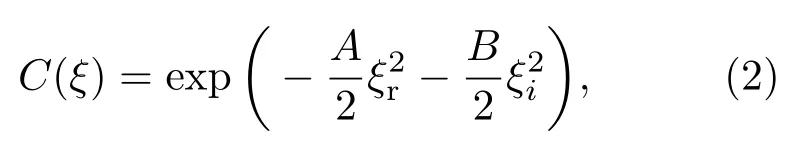
其中A和B为光场的正交分量方差.从Wely特征函数可以推导出光场的密度矩阵=进而得到光场的光子数分布:

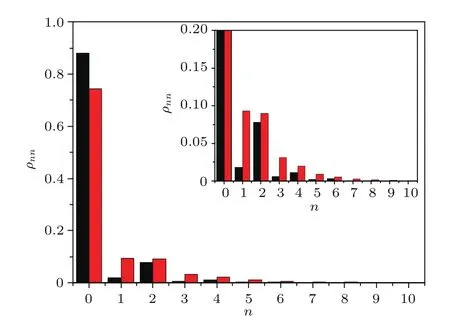
图5 极大似然估计重构(黑色直方图)和理论计算(红色直方图)得到的真空压缩态光子数分布(内插图是光子数分布的局部放大图,ρnn取值范围在0—0.2之间)Fig.5.Photon number distribution of the vacuum squeezed state obtained by maximum likelihood estimation(black histogram)and theoretical calculation(red histogram).The inset is the partial enlarged detail of photon number distribution,the value range of ρnnis 0–0.2.

Wigner函数是量子态在相空间的一种准概率分布函数.Wigner函数与密度矩阵之间的关系为

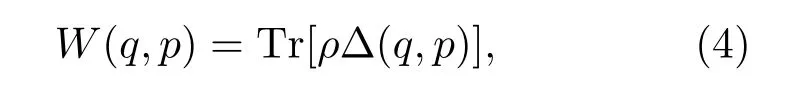
其中为Wigner算符,a+和a为光场的产生和湮灭算符,将极大似然重构得到的密度矩阵代入(4)式,计算出对应的Wigner函数,如图6(a1)所示,Wigner函数最大值为0.309.Wigner函数最大值决定于压缩场的偶数态和奇数态光子概率:

式中Peven和Podd分别是偶数态和奇数态光子概率.极大似然重构得到偶数态的概率为0.974,偶数态的概率为0.026,由关系式(5)可得Wmax=0.302,与Wigner函数最大值基本一致.图6(a2)是极大似然重构Wigner函数对应的等高线图,其中黑实线为峰值处的等高线,表示产生压缩态的噪声起伏范围;黑虚线为真空态的噪声起伏范围.从图6(a2)可以看到q分量噪声被压缩,其标准差约为真空态的64.4%,对应−3.8 dB的压缩;而p分量噪声被放大,其标准差约为真空态的1.64倍,对应4.3 dB的反压缩.

理论上光场的Wigner函数和Wely特征函数的关系可用下式描述:

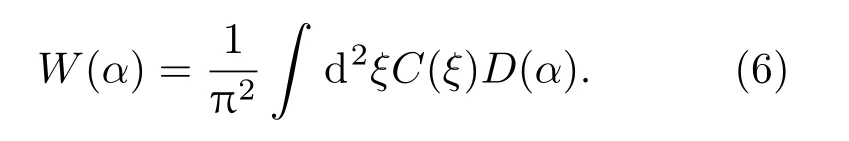
将单模真空压缩场的Wely特征函数(2)代入(6)式得到Wigner函数:

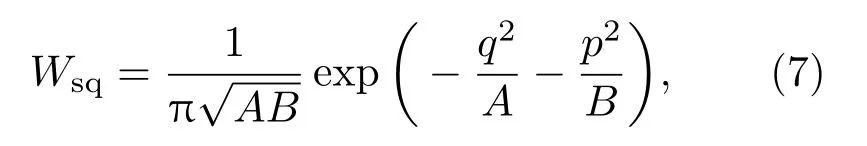
将A=0.5和B=3.8代入(7)式,得到理论重构真空压缩态的Wigner函数,如图6(b1)所示,Wigner函数最大值为0.231.极大似然重构得到的Wigner函数最大值大于理论计算结果,起源于极大似然偶数光子态概率(0.974)大于理论计算值(0.863).图6(b2)是理论计算Wigner函数对应的等高线图,黑实线为峰值处的等高线;理论计算得到噪声范围的短轴和长轴均大于极大似然重构结果.极大似然估计重构得到的光子分布和Wigner函数与理论计算结果之间的差异,可能原因有以下三方面:1)正交分量的测量过程中,相位扫描不均匀;2)数据采集过程中低频电子学噪声没有完全过滤掉;3)正交分量测量点数不够多.

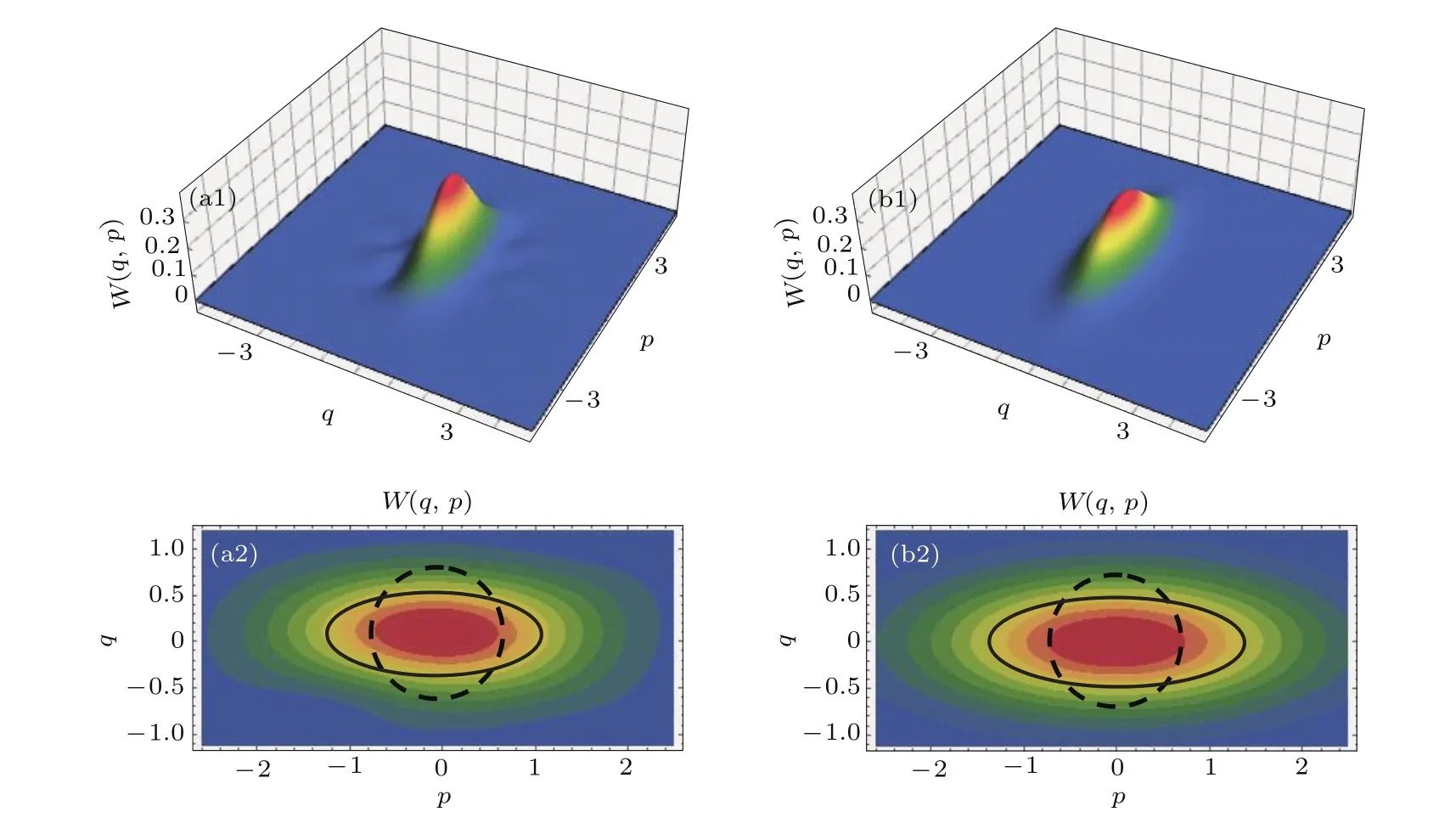
图6 (a1),(a2)分别为从极大似然估计重构得到的压缩态Wigner函数和等高线图;(b1),(b2)分别为从理论计算得到的压缩态Wigner函数和等高线图Fig.6.(a1)and(a2)are the Wigner function and the contour plot of the squeezed state obtained by maximum likelihood estimation,respectively;(b1)and(b2)are the Wigner function and the contour plot of the squeezed state obtained by theoretical calculation,respectively.

4 结 论

利用基于PPKTP晶体的OPO,产生了795 nm的真空压缩光场,波长与铷原子D1跃迁线相对应.实验上观察到−3 dB的压缩,通过改善PPKTP晶体的通光面镀膜,压缩度可进一步提高.利用极大似然估计法对压缩态的密度矩阵进行了重构,得到了压缩态的光子数分布以及相空间的Wigner函数.理论上计算了真空压缩态的光子数分布和Wigner函数,并将理论计算结果和极大似然重构结果进行了分析和比较.下一步将降低OPO腔内损耗,提高压缩态纯度,在此基础上开展猫态产生的实验研究.

参考文献

[1]Taylor M A,Janousek J,Daria V,Knittel J,Hage B,Bachor H A,Bowen W P 2013Nat.Photon.7 229

[2]Eberle T,Steinlechner S,Bauchrowitz J,Händchen V,Vahlbruch H,Mehmet M,Müller-Ebhardt H,Schnabel R 2010Phys.Rev.Lett.104 251102

[3]Pooser R C,Lawrie B 2015Optica2 393

[4]Braunstein S L,van Loock P 2005Rev.Mod.Phys.77 513

[5]Furusawa A,Sørensen J L,Braunstein S L,Fuchs C A,Kimble H J,Polzik E S 1998Science282 706

[6]Duan L M,Lukin M D,Cirac J I,Zoller P 2001Nature414 413

[7]Brask J B,Rigas I,Polzik E S,Andersen U L,Sørensen A S 2010Phys.Rev.Lett.105 160501

[8]Fleischhauer M,Lukin M D 2000Phys.Rev.Lett.84 5094

[9]Yang S J,Wang X J,Bao X H,Pan J W 2016Nat.Photon.10 381

[10]Chen Y H,Lee M J,Wang I C,Du S W,Chen Y F,Chen Y C,Yu I A 2013Phys.Rev.Lett.110 083601

[11]Honda K,Akamatsu D,Arikawa M,Yokoi Y,Akiba K,Nagatsuka S,Tanimura T,Furusawa A,Kozuma M 2008Phys.Rev.Lett.100 093601

[12]Appel J,Figueroa E,Korystov D,Lobino M,Lvovsky A I 2008Phys.Rev.Lett.100 093602

[13]Mehmet M,Ast S,Eberle T,Steinlechner S,Vahlbruch H,Schnabel R 2011Opt.Express19 25763

[14]Aoki T,Takahashi G,Furusawa A 2006Opt.Express14 6930

[15]Han Y S,Wen X,He J,Yang B D,Wang Y H,Wang J M 2016Opt.Express24 2350

[16]Takeno Y,Yukawa M,Yonezawa H,Furusawa A 2007Opt.Express15 4321

[17]Burks S,Ortalo J,Chiummo A,Jia X J,Villa F,Bramati A,Laurat J,Giacobino E 2009Opt.Express17 3777

[18]Mikhailov E E,Novikova I 2008Opt.Lett.33 1213

[19]Ries J,Brezger B,Lvovsky A I 2003Phys.Rev.A68 025801

[20]Barreiro S,Valente P,Failache H,Lezama A 2011Phys.Rev.A84 033851

[21]Horrom T,Singh R,Dowling J P,Mikhailov E E 2012Phys.Rev.A86 023803

[22]Slusher R E,Hollberg L W,Yurke B,Mertz J C,Valleys J F 1985Phys.Rev.Lett.55 2409

[23]Swaim J D,Glasser R T 2017Phys.Rev.A96 033818

[24]Wen F,Li Z P,Zhang Y Q,Gao H,Che J L,Abdulkhaleq H,Zhang Y P,Wang H X 2016Sci.Rep.6 25554

[25]Tanimura T,Akamatsu D,Yokoi Y 2006Opt.Lett.31 2344

[26]Hétet G,Glöckl O,Pilypas K A,Harb C C,Buchler B C,Bachor H A,Lam P K 2007J.Phys.B:At.Mol.Opt.Phys.40 221

[27]Vogel K,Risken H 1989Phys.Rev.A40 R2847

[28]Beck M,Smithey D T,Raymer M G 1993Phys.Rev.A48 R890

[29]Smithey D T,Beck M,Cooper J,Raymer M G 1993Phys.Rev.A48 3159

[30]Lvovsky A I,Raymer M G 2009Rev.Mod.Phys.81 299

[31]Lvovsky A I 2004J.Opt.B:Quantum Semiclass.Opt.6 S556

[32]Drever R W P,Hall J L,Kowaiski F V,Hough J,Ford G M,Munley A J,Ward H 1983Appl.Phys.B31 97

[33]Boulanger B,Rousseau I,Fève J P,Maglione M,Ménaert B,Marnier G 1999IEEE J.Quantum Electron.35 281