基于MATLAB和Creo的三片式平行分度凸轮的设计

李建功，冯敦敦

(华北理工大学 机械工程学院，河北 唐山 063210)

0 引言

随着科技的进步和工业的发展，传统的机械行业已经发生了很大的变化，半自动、全自动机械及生产线的应用范围不断扩展，数量不断增加，在这些生产线中分度机构显得尤为重要。由于三片式平行分度凸轮机构具有分度精度高、运动性能好等特点，在分度凸轮机构的实际应用中占据着重要的位置，被广泛应用于食品、包装等自动机械中[1]。

国内外学者对分度凸轮机构的设计做了大量的研究工作并取得了很多优秀成果。文献[2]对三片式平行分度凸轮机构基本参数及凸轮廓线的形成做了详细论述。文献[3]对平行分度凸轮机构的基本参数及运动条件有着详细的介绍。文献[4]采用反转法导出平行分度凸轮机构通用计算公式。运用MATLAB语言编程，绘制出轮廓曲线，通过语言编程生成.ibl格式的文件导入Creo中生成双头式平行分度凸轮的实体模型。文献[5]对如何应用MATLAB，将生成的数据导入Creo中并实现平行分度凸轮机构参数化建模做了阐述。

本文首先选定凸轮运动规律，建立固定坐标系和动坐标系，通过每个滚子在固定坐标系的初始位置角的不同得出每个滚子在动坐标系的位置角，结合其运动规律得出每个滚子圆心的坐标公式。运用MATLAB编程画出每个滚子的轨迹曲线，轮廓曲线即为凸轮与滚子啮合过程中滚子外圆形成的包络线，通过每三个滚子便可得出一片凸轮的理论轮廓曲线，再减去滚子半径即可得到一片凸轮的实际轮廓曲线。通过将MATLAB生成的.ibl格式文件导入Creo中就完成了凸轮的三维实体建模。

1 凸轮轮廓方程的建立

1.1 三片式平行分度凸轮机构的基本参数

在建立凸轮轮廓曲线前，先介绍该机构的几个基本参数：

(1) 中心距c：凸轮轴线与分度盘轴线的距离。

(2) 分度数n和分度角τh：分度数指分度盘在回转一周的过程中转动或停歇的次数，一个分度中分度盘转过的角度为分度角，显然τh=±2π/n。本文中的三片式分度凸轮分度数n=1，分度角τh=2π。

(3) 动静比kd和凸轮动程角θh：动静比是在一个分度中分度盘运动时间与静止时间的比值，凸轮动程角是凸轮在分度盘运动时间内转过的角度。

(4) 分度盘滚子数nr和凸轮头数Gm：分度盘滚子数为分度盘上的滚子总数；凸轮头数为每一个分度凸轮拨过的滚子数，即Gm=nr/n。

1.2 三片式平行分度凸轮机构轮廓曲线的形成原理

三片式平行分度凸轮机构是由三片主动凸轮和三层分度盘从动滚子组成的机构，每片凸轮以此推动相应滚子来完成机构的工作，因此，每个滚子在主动凸轮上都有其相应的轨迹曲线，即一条完整的凸轮工作轮廓曲线是由多条凸轮廓线相交组合而成的。以第一片凸轮为例，其对应的工作滚子为1、4、7，如图1所示，首先滚子1与凸轮A点接触并沿凸轮A-B段轨迹运动，当滚子1离开B点时，滚子4与B点接触并沿凸轮B-C-D段轨迹运动，当滚子4离开D点时，滚子7与D点接触并沿凸轮D-E-F段轨迹运动，当滚子7离开F点时，滚子1与凸轮F点接触并沿凸轮F-G-H段轨迹运动，当它与H点分离时分度盘完成一次步进运动，此刻开始，分度盘进入停歇期即H-A段轨迹。

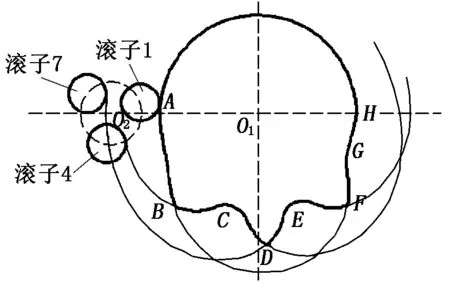
图1 第一片凸轮轮廓曲线

1.3 三片式平行分度凸轮机构轮廓曲线方程的建立

凸轮匀速转动，按变余弦运动规律做间歇分度运动，凸轮转过角度为α，与分度盘转过的角度θ之间存在函数关系：

θ=F(α).

(1)

建立三片式平行分度凸轮机构的二维简图，以凸轮回转中心点为原点建立固定坐标系xoy和动坐标系x1oy1。中心距为c，分度数为n，滚子数为nr，按顺时针方向排序，i=1,2,3,…,nr。滚子半径为rr，均匀分布在半径为rd的分度盘上，参考文献[4]可知第i个滚子的初始位置为：

(2)

根据反转法原理，假设凸轮不动，分度盘以均匀速度绕凸轮轴线逆时针转动，在动坐标系x1oy1中，第i个滚子的位置角θi为：

θi=θi0+θ.

(3)

设分度盘转过的角度θ服从变余弦运动规律函数，即：

(4)

第i个滚子在固定坐标系中的圆心坐标为：

(5)

2 凸轮轮廓曲面曲线的绘制

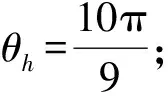
(6)

根据式(5)，运用MATLAB编程，得到三个滚子运动轨迹程序如下：

滚子1：

t=0:0.001:1;

a=pi*t;

x=160*cos(a)+34*cos(pi*19/9-pi*cos(9*a/10)+a);

y=160*sin(a)+34*sin(pi*19/9-pi*cos(9*a/10)+a);

z=0*t;

plot3(x,y,z);

滚子4：

t=0:0.001:1;

a=pi*t;

x=160*cos(a)+34*cos(pi*13/9-pi*cos(9*a/10)+a);

y=160*sin(a)+34*sin(pi*13/9-pi*cos(9*a/10)+a);

z=0*t;

plot3(x,y,z);

滚子7：

t=0:0.001:1;

a=pi*t;

x=160*cos(a)+34*cos(pi*7/9-pi*cos(9*a/10)+a);

y=160*sin(a)+34*sin(pi*7/9-pi*cos(9*a/10)+a);

z=0*t;

plot3(x,y,z);

将时间进行无因次化表达，其中t为对应周期为1的瞬时时间，得到的第一片凸轮理论轮廓如图2所示。

图2 第一片凸轮理论轮廓

3 凸轮的三维实体建模

在MATLAB中输入滚子轨迹程序后，需将生成的坐标点保存成 .ibl格式的文件，再导入Creo中完成三维实体建模。以滚子1为例，其 .ibl格式文件的创建程序如下：

t=0:0.001:1;

a=pi*t;

x=160*cos(a)+34*cos(pi*19/9-pi*cos(9*a/10)+a);

y=160*sin(a)+34*sin(pi*19/9-pi*cos(9*a/10)+a);

z=0*t;

plot3(x,y,z);

hold on;

M=[x;y;z]';

b=size(M);

M=[floor(1:b(1:1));M']';

dlmwrite('data.ibl',M,'delimiter',' ','newline','pc');

将.ibl格式的文件以记事本的方式打开，如图3所示。

图3 滚子1中心坐标

打开Creo运行程序，新建零件，选择【点】/【偏移坐标系】，建立笛卡尔坐标系，点击【导入】将滚子1的.ibl格式文件导入，得到坐标点分布图，然后选择【基准】/【曲线】/【来自点的曲线】将点连成一条曲线，将点隐藏后得到滚子1的轨迹，同样的方法将其余两个.ibl文件导入得到第一片凸轮的轮廓曲线，如图4所示。

删除多余线段然后进行三维建模，得到第一片凸轮的三维实体，如图5所示。

同样，根据上述过程可完成第二片和第三片凸轮的实体建模。

图4第一片凸轮廓线图5第一片凸轮实体

4 结论

本文采用一种比较简单的方法来推导出三片式平行分度凸轮机构滚子中心的坐标点，运用MATLAB得到滚子中心的运动轨迹，并结合Creo软件完成了该机构的三维实体建模。该方法还可应用到其他分度凸轮机构中，通用性强，易理解，简化了分度凸轮机构的三维建模过程。

参考文献：

[1] 潘同庆.平行分度凸轮机构的轮廓设计和动力学分析[D].青岛：中国海洋大学,2009:1-3.

[2] 李洪添.三片式平行分度凸轮传动装置CAD/CAM系统研究[D].南京：南京航空航天大学,2011:6-8.

[3] 刘昌祺,牧野洋，曹西京.凸轮机构设计[M].北京：机械工业出版社，2005.

[4] 赵浩东.平行分度凸轮的动力学研究[D].济南：济南大学，2011:22-25.

[5] 李建功,王晓月.基于MATLAB和Creo的圆柱分度凸轮的设计[J].煤矿机械，2015,36(3):38-40.