2018年高考文科数学模拟试题

黄伟军

本试卷分为第I卷（选择题）和第II卷（非选择题）两部分.

第I卷

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的

1. 已知集合A={x|x2-3x<0}，{B=x|x-2≥0}则A∩B为

（ ）

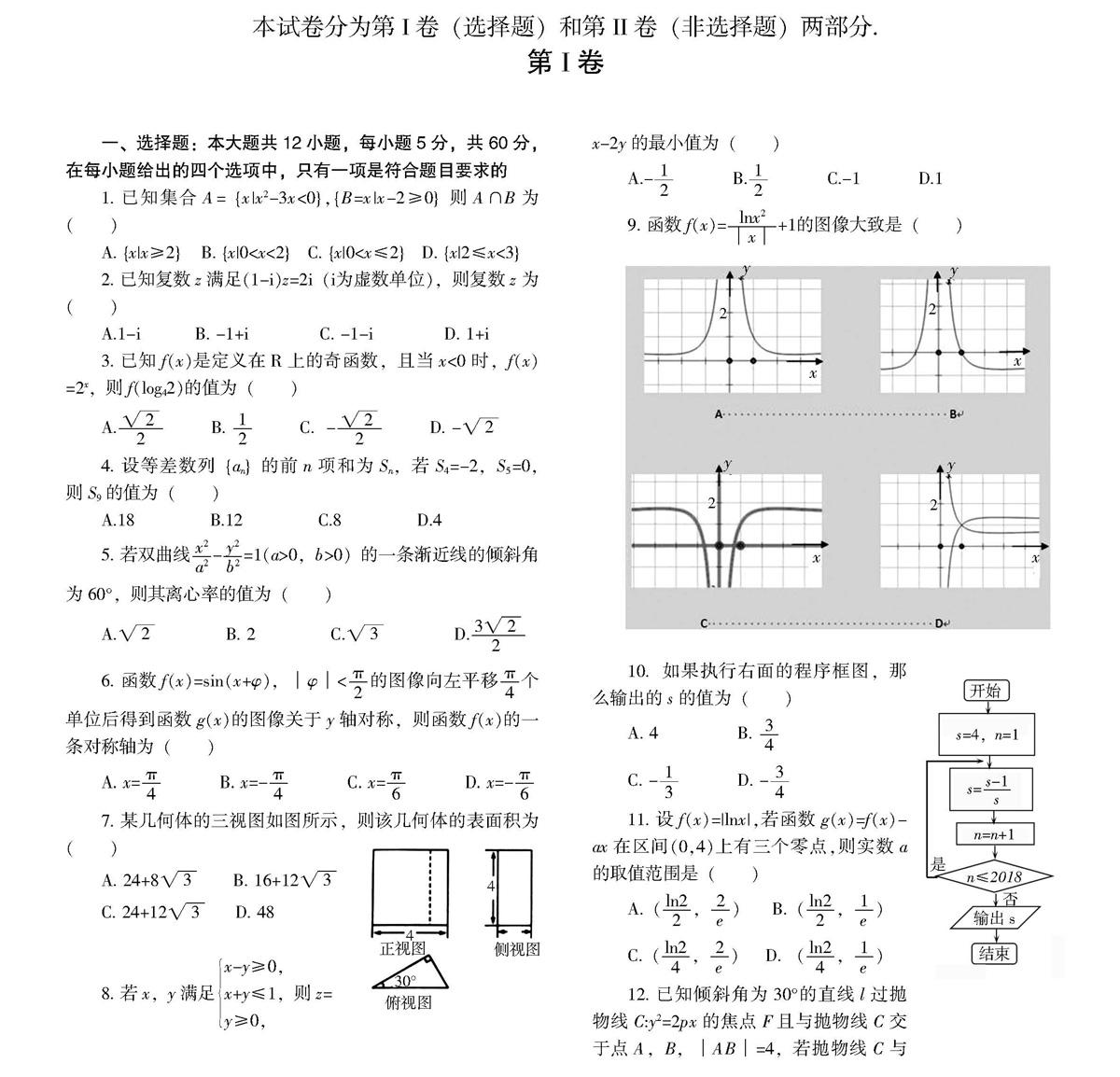
A. {x|x≥2} B. {x|0

2. 已知复数z满足（1-i）z=2i（i为虚数单位），则复数z为（ ）

A.1-i B. -1+i C. -1-i D. 1+i

3. 已知f（x）是定义在R上的奇函数，且当x<0时，f（x）=2x，则f（log42）的值为（ ）

A.■ B. ■ C. -■ D. -■

4. 设等差数列{an}的前n项和为Sn，若S4=-2，S5=0，则S9的值为（ ）

A.18 B.12 C.8 D.4

5. 若双曲线■-■=1（a>0，b>0）的一条渐近线的倾斜角为60°，则其离心率的值为（ ）

A.■ B. 2 C.■ D.■

6. 函数f（x）=sin（x+？渍），│？渍│<■的图像向左平移■个单位后得到函数g（x）的图像关于y轴对称，则函数f（x）的一条对称轴为（ ）

A. x=■ B. x=-■ C. x=■ D. x=-■

7. 某几何体的三视图如图所示，则该几何体的表面积为（ ）

A. 24+8■ B. 16+12■

C. 24+12■ D. 48

8. 若x，y满足x-y≥0，x+y≤1，y≥0，则z=x-2y的最小值为（ ）

A.-■ B.■ C.-1 D.1

9. 函数f（x）=■+1的图像大致是（ ）

10. 如果执行右面的程序框图，那么输出的s的值为（ ）

A. 4 B. ■

C. -■ D. -■

11. 设f（x）=|lnx|，若函数g（x）=f（x）-ax在区间（0，4）上有三个零点，则实数a的取值范围是（ ）

A.（■，■） B.（■，■）

C.（■，■） D. （■，■）

12. 已知倾斜角为30°的直线l过抛物线C：y2=2px的焦点F且与抛物线C交于点A，B，│AB│=4，若抛物线C与圆O：x2+y2-10x+25-R2=0（R>0）有四个不同的交点，则R的取值范围是（ ）

A.（■，10） B. （■，10）

C. （■，5） D. （■，5）

本卷包括必考题和选考题两部分，第13题-第21题为必考题，每个试题考生都必须做答，第13题-第21题为必考题，每个试题考生都必须做答，第22题-第23题为选考题，考生根据要求做答.

二、填空题：本大题共4小题，每小题5分，共20分

13. 若向量■=（■，1），■=（0，-1），■=（1，t），若（■-2■）∥■，则■与■的夹角等于 .

14. 设等比数列{an}的前n项和为Sn，若■=■，则■= .

15. 下列表格提供了某四个家庭2017下半年的总收入x（万元）与总投资y（万元）的四组对照数据.

根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程为y=0.7x+0.35，则m的值为 .

16. 侧棱和底面边长均为2■的正三棱锥S-ABC，它的四个顶点S，A，B，C在同一球面上，则这个球的表面积的值为 .

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答

（一）必考题：60分

17.（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，已知■+■=■.

（1）求b；

（2）若sin（■+B）=1，S△ABC=■■，求a，c的值.

18. （本小题满分12分） 某批发商对刚从甲与乙两个水产养殖场收购的一批小龙虾分别随机抽取了40只进行单个小龙虾的重量的检测，得到40只小龙虾重量的频数分布表和频率分布图如下：

甲水产养殖场抽取的40只小龙虾的重量的频数分布表

B筐抽取的40只小龙虾的重量的频率分布图：

19. （本小题满分12分）如图，三棱锥中P-ABC，BC=2，AC=2■，AB=4，点D为线段AB上一点，且AD=3DB， PD⊥平面ABC，PD=AD.

（1）求证：平面PAB ⊥平面PCD.

（2）求三棱锥A-PBC的体积.

20. （本小题满分12分）已知椭圆E：■+■=1的一个焦点为F1（-■，0），O为坐标原点，P（■，-■）为椭圆上一点.

（1）求椭圆E的方程；

（2）设点A，B，C在E上运动，A与B关于原点对称，且 | AC | = | CB |，求？駐ABC的最小面积.

21. （本小题满分12分）设函数f（x）=（x2-2ax）ln x+2x2.

（1）若曲线f（x）在点（1， f（1））处的切线与直线y=-■x+1互相垂直，求a的值；

（2）若对任意x∈[1，+∞），不等式 2f（x）>3x2+a恒成立，求实数a的取值范围.

请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题计分.

22. （参数方程与极坐标）（本小题满分10分）在直角坐标系xOy中，曲线C1：x=cos？琢，y=1+sin？琢（？琢为参数），以该直角坐标系的原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的方程为y=-■x，曲线C2 的极坐标方程为ρ=-2cos？兹+2■sin？兹.

（1）求曲线C1和C2 的直角坐标方程；

（2）设直线l交曲线C1于O，A两点，直线l交曲线C2于O，B两点，求 | AB | 的长.

23.（不等式选讲）（本小题满分10分）如图是函数f（x）的图像， 函数g（x）=x2.

（1）写出函数f（x）的解析式；

（2）当x∈[-2， 5]时，不等式m≥f（x）+g（x）恒成立，求m的最小值.

2018年高考文科数学模拟试题参考答案

提示：

1. A={x|x2-3x<0}={x|0

2. 方法1；设z=a+bi （a， b∈R），由（1-i）z=2i得（1-i）（a+bi）=2i，即a+bi-ai+b=2i，因此a+b=0，b-a=2，解得a=-1，b=1，所以z=-1+i，选B.

方法2；由（1-i）z=2i，得z=■=-1+i，选B.

3. f（x）是定义在R上的奇函数， 故f（-x）=-f（x）， 当x>0时，-x<0，则f（-x）=2-x，即f（-x）=-f（x）=2-x，得到f（x）=-2-x，因为log 4 2=■，故f（log 4 2）=f（■）=-2■=-■，选C.

4. 方法1：由题意可得4a1+■d=-2，5a1+■d=0，即2a1+3d=-1，a1+2d=0，解得a1=-2，d=1，故S9=9a1+■d=9×（-2）+36=18，选A.

方法2：由已知得，a5=S5-S4=2，因为数列{an}为等差数列，所以S9=■=■=9a5=18，选A.

5. 依题意可得双曲线的一条渐近线方程为y=■x，故■=tan60°=■，故■=3，离心率为e=■=■=■=■=2，选A.

6. 函数f（x）=sin（x+？渍）的图像向左平移■个单位后，所得图像对应的函数解析式为g（x）=sin（x+■+？渍）. 再由所得g（x）的图像关于y轴对称，可得g（x）为偶函数，故？渍+■=k？仔+■，k∈Z， 即？渍=k？仔+■， k∈Z，又|？渍|<■， 故？渍=■，可得函数f（x）=sin（x+■），函数f（x）的一条对称轴为x=■，选A.

7. 由三视图可得该几何体是三棱柱，底面是有一个角是30°斜边为4且斜边上的高为■的直角三角形，可得三角形另外两边为2，2■，三棱柱的高为4，该几何体的表面积为2×■×4×■+（2+2■+4）×4=24+12■. 选C.

8. 先作出x-y≥0，x+y≤1，y≥0表示的平面区域，如图三角形阴影部分表示，目标函数z=x-2y可化为y=■x-■z，平移直线y=■x，可知当直线y=■x-■z 经过点A时纵截距最大，z取得最小值，由x-y≥0，x+y≤1，可得x=■，y=■，即A（■， ■），故zmin=■-2×■=-■. 选A.

9. f（-x）=■+1=■+1=f（x）是偶函数，排除D. 当x>0时，f（x）=■+1，则 f′（x）=■ = ■，当0

10. s=4，n=1？圯s=■=■，n=2？圯s=■=-■，n=3？圯s=■=4，n=4？圯s=■=■，n=5，周期为3，依题意可得n=2018时，输出s，因为2018=672×3+2，所以输出s=■，选B.

11. 由题意，当g（x）=0，即f（x）=ax时，若曲线y=f（x）与y=ax相切时，切点为（e，1），得到a=■，可知，当0■，故所求a的取值范围为（■，■），选B.

12. 设A（x1，y1），B（x2，y2），焦点F（■，0），直线l的方程为y=■（x-■），

联立y=■（x-■），y2=2px可得x2-7px+■=0，故x1+x2=7p，由拋物线定义可得|AB|=x1+■+x2+■=7p+p=4，解得p=■，故抛物线方程为y2=x.

将抛物线C∶y2=x与圆O∶x2+y2-10x+25-R2=0的方程联立，消去y2，整理得x2-9x+25-R2=0（*）. 抛物线与圆有四个不同的交点的充要条件是：方程（*）有两个不相等的正根即可，即？驻=81-4（25-R2）>0，25-R2>0，解得■

13. ■π；14. -■；15. 4；16. 18π.

答案提示：

13. 设■与■的夹角为？琢，■-2■=（■，3），因为（■-2■）//■，故■t-3=0，解得t=■，即c=（1，■），故cos？琢=-■，因为0≤？琢≤π，故？琢=■π.

14. 法1：S3=■，S6=■，S9=■，

由■=■可得q3=-■，设■=t，则S3=■t，S6=■t，S9=■t，

则■=■=-■.

法2：因为■=■，所以S6=■S3，S6-S3=-■S3，由等比数列的性质得S3，-■S3，S9-■S3，成等比数列，所以■■=S3（S9-■S3），得S9-■S3=■S3，所以■=■=-■ .

15. x=■=■=4.5，y=■=■，因为样本中心点（x，y）一定在回归直线上，所以■=0.7×4.5+0.35，解得m=4.

16. 设球的半径为r，过A作AD垂直于BC，垂足为D，过S作底面ABC的垂线SO1，垂足为O1，依题意可得O1在直线AD上，AD=■×2■=3，AO1=■×■×2■=2，故SO1=■=2■，设O是球心，连接OA，依题意可得|OA|=r，|OO1|=■×2■-r=2■-r，在直角三角形OO1A中，则有22+（2■-r）2=r2，得到r=■■，故这个球的表面积为4π×（■■）2=18π.

三、解答题：解答应写出文字说明、证明过程或演算步骤

17. 解析：（1）方法1：由■+■=■可得■=■，即■=■，故■=■，得到b=■.

方法2：由余弦、正弦定理可得■+■=■，化简得2b=1，得到 b=■.

（2）由sin（■+B）=1，解得B=■.

由S？驻ABC=■可得■acsin■=■，解得ac=■……（1）

因为b=■，由余弦定理可得b2=a2+c2-2accosB，即■=a2+c2-ac=（a+c）2-3ac……（2）

（1）代入（2）得（a+c）2=1，即a+c=1……（3）

联立a+c=1，ac=■，可得c2-2c+1=0解得c=■，故a=■.

18. 解析：（1）若把频率看作相应的概率，则：

“甲水产养殖场的小龙虾为优质”的概率为■=0.85；

“乙水产养殖场的小龙虾为优质”的概率为■=0.8，所以甲水产养殖场的小龙虾优质率高.

（2）用分层抽样的方法从乙水产养殖场重量在[1，3），[3，5），[9，11]的小龙虾中共抽取6只，则重量在[1，3）内的有2只，在[3，5）内的有3只，在[9，11]内的有1只.

记重量在[1，3）内的为x1，x2，在[3，5）的为y1，y2，y3，[9，11]的为z，从中任取2只，可能的情况有：（x1，x2），（x1，y1），（x1，y2），（x1，y3），（x1，z），（x2，y1），（x2，y2），（x2，y3），（x2，z），（y1，y2），（y1，y3），（y1，z），（y2，y3），（y2，z），（y3，z），共15种；设任取2只，至少有1只重量在[3，5）的小龙虾的概率事件为A，则事件A包含有（x1，y1），（x1，y2），（x1，y3），（x2，y1），（x2，y2），（x2，y3），（y1，y2），（y1，y3），（y1，z），（y2，y3），（y2，z），（y3，z），共12种，所以P（A）=■=■.

19. 解析：因为BC=2，AC=2■，AB=4，所以AB2=42=（2■）2+22=16，所以？驻ABC是直角三角形，故AC⊥CB，在Rt？驻ABC中，∠CAB=30°，BD=1，由AD=3DB，得AD=3，BC=2，AC=2■，由余弦定理得CD2=AD2+AC2-2AD×AC×cos30°=32+（2■）2-2×3×2■2■cos30°=9+12-18=3，故CD=■，由CD2+AD2=AC2，即3+9=12，所以CD⊥AD. 因为PD⊥平面ABC，CD？奂平面ABC，所以PD⊥CD，由PD∩AD=D，得CD⊥平面PAB，又CD？奂平面PCD，所以平面PAB⊥平面PCD.

（2）求三棱锥A-PBC的体积等价于求三棱锥P-ABC的体积.

由（1）知？驻ABC是直角三角形，BC=2，AC=2■，故？驻ABC的面积为■×2×2■=2■，因为PD⊥平面ABC，PD=DA，可得PD=DA=3，故三棱锥P-ABC的体积为■×2■×3=2■，即三棱锥A-PBC的体积为2■.

20. 解析：F1（-■，0）是椭圆E：■+■=1的一个焦点， 且经过P（■，-■）.

依题意可得■+■=1，a2-b2=3，即2b4+b2-3=0，解得b2=1或b2=-3（舍去），可得a2=4，故椭圆E的方程为■+y2=1.

（2）当AB为长轴（或短轴）时，依题意知，点C就是椭圆的上下顶点（或左右顶点），此时S△ABC=■×OC×AB=2.

当直线AB的斜率存在且不为0时，设其斜率为k，直线AB的方程为y=kx，

联立方程■+y2=1，y=kx，得x2A=■，y2A=■，

所以OA2=x2A+y2A=■. 由AC=CB，知△ABC為等腰三角形，O为AB的中点，OC⊥AB，所以直线OC的方程为y=-■x，由■+y2=1，y=-■x，解得x2C=■，y2C=■，OC2=■，

S△ABC=2S△OAC=OA×OC=■×■=■.

由于■≤■=■，所以S△ABC=≥■.

当且仅当1+4k2=k2+4，即k=±1时等号成立，此时△ABC面积的最小值是■.

21. （1）因为f′（x） =（2x-2a）lnx+（x2-2ax）■+4x，所以f（1）=2，f′（1） =5-2a，曲线f（x） 在点（1，f（1） ）处的切线方程为y-2=（5-2a）（x-1），切线与直线y=-■x+1互相垂直，即5-2a=3，解得a=1.

（2）f（x）=（x2-2ax）lnx+2x2，a∈R.

所以不等式2f（x）>3x2+a等价于（2x2-4ax）lnx+x2-a>0.

方法一：令h（x）=（2x2-4ax）lnx+x2-a，x∈[1，+∞），

则h′（x）=（4x-4a）lnx+（2x-4a）+2x=4（x-a）（lnx+1）（x≥1）.

当a≤1时，h′（x）≥0，则函数h（x）在[1，+∞）上单调递增，所以h（x）min=h（1）=1-a，所以根据题意，知有1-a>0，∴a<1.

当a>1时，由h′（x）<0，知函数h（x）在[1，a）上单调减；

由h′（x）>0，知函数h（x）在（a，+∞）上单调递增.

所以h（x）min=h（a）=a2（1-2lna）-a.

由条件知，a2（1-2lna）-a>0，即a（1-2lna）-1>0.

设g（a）=a（1-2lna）-1，a>1，则g′（a）=1-2lna<0，a>1，

所以g（a）在（1，+∞）上單调递减.

又g（1）=0，所以g（a）

综上可知，实数a的取值范围为（-∞，1）.

方法二：令h（x）=（2x2-4ax）lnx+x2-a，x∈[1，+∞），

则h（x）=（2x2-4ax）lnx+x2-a>0在[1，+∞）上恒成立，所以h（1）=1-a>0，

所以a<1.

又h′（x）=（4x-4a）lnx+（2x-4a）+2x=4（x-a）（lnx+1）（x≥1），

显然当a<1时，h′（x）=>0，则函数h（x）在[1，+∞）上单调递增，所以h（x）min=h（1）=1-a>0，所以a<1.

综上可知a的取值范围为（-∞，1）.

22.

解析：（1）曲线C1的标准方程为：x2+（y-1）2=1即：x2+y2 -2y=0.

曲线C2的方程为：？籽=-2cos？兹+2■sin？兹.

即：？籽2=-2？籽cos？兹+2■？籽sin？兹？圯x2+y2=

-2x+2■y.

所以曲线C2的直角坐标方程为：（x+1）2+（y-■）2=4.

（2）解法1：由y=-■x，x2+y2-2y=0，可解得x=0，y=0或x=-■，y=■，

则OA=■=■.

同理由y=-■x，x2+y2=2x+2■y，可解得x=0，y=0或x=-2，y=2■，

则OB=■=■=4，

故 AB =OB-OA=4-■.

解法2：直线l的极坐标方程为？兹=■，

圆C1的极坐标方程为？籽=2sin？兹，

所以 OA=？籽1=2sin■=■.

圆C2的方程为？籽=-2cos？兹+2■sin？兹，

所以OB= ？籽2=-2cos■+2■sin■=4，

所以AB=？籽1- ？籽2=4-■.

23解析：（1）由图像可得解析式为f（x）=3x+5，-2≤x≤-1-■x+■，-1≤x≤2x-1.2≤x≤5

（2）当x∈[-2，5]时，不等式m≥f（x）+g（x）恒成立等价于m≥[f（x）+g（x）]max

设h（x）=f（x）+g（x），当x∈[-2，-1]时，h（x）=x2+3x+5=（x+■）■+■，故hmax（x）=hmax（-2）=hmax（-1）=3.

当x∈[-2，1]时，h（x）=x2-■x+■=（x-■）■+■，故hmax（x）=hmax（-2）=■.

当x∈[1，5]时，h（x）=x2+x-1=（x+■）■-■，hmax（x）=hmax（5）=29，

故m≥29，故m的值为29.

责任编辑 徐国坚