合成源MCSEM高阻薄层识别

李 盼 李予国*②(中国海洋大学海洋地球科学学院，山东青岛 266100； ②海洋海底科学与探测技术教育部重点实验室，山东青岛 266100)

1 引言

中国广阔的海域蕴藏着大量的石油和天然气等资源，地震勘探是探测海洋油气资源的主要地球物理方法，利用地震数据可以获得精确的地质构造信息并预测储层孔隙度，却很难判断构造中流体的性质[1，2]，而海洋可控源电磁法(Marine Controlled Source Electromagnetic，MCSEM)是探测海底油气、天然气水合物以及矿产资源的一种海洋地球物理勘探新方法[3，4]。它通过探测含油气储层与周围沉积层之间的电阻率差异引起的电磁异常，研究海底地层的电阻率分布，根据电阻率与储层含油气饱和度的关系，可推断其含油气性。利用该方法可以识别高阻油气藏，提高钻井成功率，降低勘探成本。因此，MCSEM法已成为各大石油勘探公司钻前储层评价的重要手段之一[5]。

常规海洋电磁勘探方法在深水海域用水平电偶极源向海底发射低频(0.01～10Hz)电磁信号，由布设在海底的电磁接收仪器记录来自海底地层的电场和磁场信号[6]。该方法对于深水区域海底高阻油气藏具有很高的分辨率，主要是因为巨厚的海水层可以有效消除空气波的干扰[7]。因此，早期的海洋电磁观测都集中在深水区域(海水深度大于1000m)，并取得了良好的效果[8]。然而，在浅水区(海水深度小于300m)的应用遇到了一定困难。在浅水区使用常规的水平电偶极作为发射源进行MCSEM勘探时，接收到的信号中空气波占主导地位，它掩盖了从海底介质中返回的有效信号，特别是来自高阻层中的导波信号，这严重影响了反演解释结果[9]。因此，在浅水区MCSEM资料处理中抑制空气波的影响，对提高储层识别能力具有重要意义。

合成孔径技术在雷达和声呐领域已经得到广泛应用，其核心思想是通过不同场源的相互干涉构建一个加长的合成源，并使其能量向着特定方向加强和传播。Fan等[10,11]已经证明散射场可以通过适当的相位校正和振幅校正被转向和加强。汪轩等[12]利用合成孔径与径向消除方法较好地压制了浅海可控源电磁勘探中空气波的影响。Knaak等[13，14]提出了2D合成孔径源的概念，并将其应用于三维海洋可控源电磁数据处理。Yoon等[15]和Zhdanov等[16]改进了Fan等的选取校正系数的方法，通过参数优化提高合成孔径源对电磁异常识别效果。

目前常用于MCSEM资料解释的电磁响应异常有归一化振幅、有效异常和可探测度等。归一化振幅是最常用的异常响应之一[17,18]，但计算归一化振幅时，没有考虑观测误差和噪声干扰等因素的影响[19]。鉴于此，赵慧等[20]把观测误差和噪声等干扰因素考虑在内，提出了有效异常计算方法，用于确定探测海底天然气水合物储层的MCSEM勘探参数。在深水区，基于有效异常进行MCSEM响应分析非常有效，但在浅水区效果欠佳。有效异常最明显的弱点是没有包含相位信息，刘婷婷等[21]在考虑相位的基础上定义了可探测度，并通过数值模拟证明其在浅水区可有效识别高阻薄层。

海洋电磁场数值模拟中，各向同性的地电模型可以很好地近似地下电性结构[22]。因此，本文首先利用MCSEM一维正演程序，计算浅水区不同水深模型的电磁场响应，比较了使用不同相位和振幅校正时合成源响应的归一化振幅、有效异常和可探测度对高阻层的识别能力；然后，将可探测度作为相位校正和振幅校正参数选择的基准，分别利用MCSEM二维和三维正演程序[23-25]计算二维和三维模型采用相对最佳组合校正参数时的合成源可探测度。结果表明利用可探测度选择校正参数能够有效地提高MCSEM合成源干涉法对高阻体的识别能力。

2 MCSEM合成源干涉法

在MCSEM勘探中，利用不同发射源电磁信号的干涉构成一个加长的合成源，其表达式[26]为

(1)

式中： 某一位置r处角频率为ω的合成源信号SA(r,ω)是由r1到rN处发射源的信号叠加而成；sn(r,rn,ω)表示第n个源在rn处产生的电磁场信号，并且每个源产生的电磁场都经过振幅修正an和相位校正φn。

令an=exp(-c2αΔx)、φn=-c1αΔx，则合成源信号可以进一步表示为[26]

sn(x,xn,ω)

(2)

图1 MCSEM电磁信号传播路径示意图

根据MCSEM信号主要传播路径，可以解释合成孔径方法突出高阻异常和抑制空气波的原因。由图1可知，电磁信号从发射源(Tx)到达接收站(Rx)主要有三种途径(分别见图1中的①、②、③)： (a)发射源电磁信号垂直穿过海水层到达海空界面，然后沿海平面滑行一段距离，再折射垂直向下穿过海水层到达接收站，这部分被接收到的电磁信号称作空气波； (b)电磁信号从发射源穿过海水层直接到达接收站； (c)电磁信号经过海水层和海底地层后返回至接收站。其中，从海底地层传播回来并被接收站接收到的电磁信号才是有用信号。可用于研究海底地质构造及圈闭含油气情况。

当对合成源的单源电磁信号进行相位校正时电磁场将发生转向，电磁信号传播路径会发生改变，因此通过选择合适的相位校正系数可以使储层响应得到加强、空气波得到抑制。其主要原因有两个：首先，电磁场能量大部分是垂直于电偶极源向外传播的，因此当发射源转向高阻体时，相比发射源水平时有更多的能量集中到高阻体，于是接收站接收到的有效信息则相对增加；其次，当电磁场发生转向时，竖直向上传播的能量减少，在海面与空气的分界面上转换为空气波的能量相应减少，因此空气波得到抑制。同时，通过适当的振幅校正可以调谐不同发射源电磁信号之间的相互干涉，使干涉增强，可以进一步抑制空气波，增强目标体的异常响应。

3 一维模型合成源电磁响应异常分析

3.1 电磁响应异常

目前用于MCSEM资料解释的电磁响应异常有归一化振幅、有效异常和可探测度等。归一化振幅是指含高阻层模型与背景模型的电磁场振幅之比

(3)

式中：|Eres|指含高阻层模型的电磁场振幅； |Eback|指背景模型的电磁场振幅。对于深水模型，若R大于1，则表明海底下方可能存在高阻层。但当海水深度变浅时，由于空气波影响增强，常规的归一化振幅对地下高阻层的识别能力变弱。另外，在计算归一化振幅时，由于没有考虑观测误差和海底电磁数据记录仪及其测量系统误差等因素的影响，因此依据归一化振幅解释MCSEM资料时可能会产生较大偏差。

裴建新等[19]综合考虑了海底电磁采集站方位观测误差、数据记录仪和测量系统误差的影响，定义了有效异常

(4)

其中噪声表达式为[19]

(5)

式中：Enoise为电磁场的噪声；Erel为电磁场振幅的相对误差，通常假定其为背景场振幅值的5%；Erol为由海底电磁采集站电场测量臂或磁场传感器方向的不确定性引起的误差；Eabs为绝对误差，即海底电磁站数据记录仪的本底噪声，通常设为1.0×10-16V·A-1·m-2。

由于电磁场为复数场，它既包含振幅信息也包含相位信息，而归一化振幅和有效异常都没有考虑相位信息。因此，在计算有效异常的基础上，为了进一步提高对高阻油气层的识别能力，刘婷婷等[21]将相位信息考虑在内，对有效异常公式进行了修正，定义了可探测度

(6)

D反映了对高阻油气层的可探测程度。D值越大，表明高阻油气层越容易被探测到。刘婷婷等[21]计算了不同水深情况下一维水合物模型的MCSEM归一化振幅、有效异常和可探测度。结果表明，在深水环境下利用归一化振幅、有效异常和可探测度均可识别水合物高阻薄层；但在浅水环境下，归一化振幅和有效异常受空气波影响畸变严重，不能很好地识别高阻薄层，而空气波对可探测度影响较小，在浅水区利用可探测度有利于识别水合物高阻薄层。

3.2 一维模型合成源响应分析

设计如图2所示的海洋一维层状模型，海水层厚hsw是可变的，分别设为200、100、50m。海底之下第二层电阻率若等于100Ω·m，则代表高阻模型，若电阻率为1Ω·m，则代表背景模型。基底为均匀半空间。

图2 变海水层厚一维层状模型

采用Inline模式(轴向)观测系统，51个水平电偶极源(Tx)均位于海底上方20m处，间距为100m，分布范围为-2.5～2.5km，发射频率为0.25Hz； 201个接收站(Rx)位于海底，间距为200m，分布范围为-20～20km。分别计算海水层厚为50、100和200m三种情况下合成源响应的归一化振幅、有效异常和可探测度，并对这些参数进行对比分析。

当对合成源进行相位校正(c2=0)时，归一化振幅最大值(Rmax)、有效异常最大值(Smax)、可探测度最大值(Dmax)随相位校正系数c1的变化曲线分别如图3上所示。由图可见： ①对于同一相位校正系数，三个电磁响应异常最大值都随着海水层厚减小而降低； ②三个参数的最大值都呈现减小—增大—减小的规律； ③当相位校正系数c1约为0.7时，校正效果达到最佳，当等于0.3时，效果最差；④通过选择合适的c1值，高阻层的异常响应可以提高10%～20%。当对合成源进行振幅校正(即c1=0)时，Rmax、Smax、Dmax随c2的变化曲线如图3下所示。由图可见： ①对于同一振幅校正系数，三个电磁响应异常最大值都随着海水层厚减小而降低； ②三个电磁响应异常最大值曲线都呈现减小—增大—减小的趋势； ③当c2约为0.5时，校正效果最差，而当c2=0时，校正效果最佳。

为了对比上述三个参数在同一条件下的特征差异，对图3重新组合，得到图4。由图4可见，在三种不同海水层厚下，无论是进行合成源相位校正还是振幅校正，可探测度参数的效果最佳，有效异常次之，归一化振幅最差。

图3 海水层厚分别为50、100和200m三种情况下合成源产生的Rmax(a)、Smax(b)、Dmax(c)随c1(上)和c2(下)变化曲线

图4 海水层厚分别为50(a)、100(b)和200m(c)三种情况下合成源产生的Rmax、Smax、Dmax随c1(上)和c2(下)变化曲线

图5 水层厚度分别为50m(上)、100m(中)、200m(下)时不同校正参数(c1、c2)组合时合成源电场Ey分量归一化振幅最大值Rmax(a)、有效异常最大值Smax(b)、可探测度最大值Dmax(c)分布图

综上可知，在对不同海水层厚模型合成源进行相位校正或振幅校正时，D相比于R和S对高阻层具有更高的识别能力。

下面分析对合成源进行相位与振幅综合校正时上述三个参数的特征。

图5为三种海水层厚情形下不同相位校正与振幅校正参数组合时得到的合成源电场Ey分量上述三个参数最大值的分布图，激发频率为0.25Hz。由图可知，合成源归一化振幅最大值Rmax相对较高的区域分布范围较小且区域不连续；合成源有效异常最大值Smax和可探测度最大值Dmax的高值分布范围较大且相对连续，而且随着海水深度加大，其分布范围也随之增大。可见，采用振幅校正系数c1和相位校正系数c2综合校正时，Dmax分布范围最大、连续性最好，Smax次之，Rmax最差。

4 二维模型合成源电磁响应异常

设计的二维模型如图6所示，海水电阻率为0.3Ω·m，海水层厚为50m，二维体埋深为1000m，厚度为100m，其在y方向的延伸范围为-2～2km，即宽度为4km。若二维体电阻率为100Ω·m，代表高阻体模型， 若电阻率为1Ω·m，则代表背景模型。

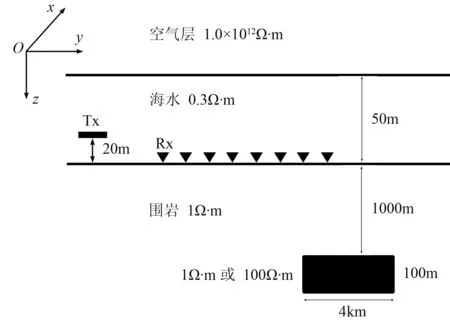
图6 二维海洋地电模型

采用Inline采集模式，假定51个水平电偶极源(Tx)均位于海底上方20m处，分布范围为-9～-4km，间距为100m，发射频率为0.25Hz，126个接收站(Rx)位于海底，分布范围为-10～15km，间距为200m。分别分析单源、简单合成源、相位校正合成源以及相位与振幅组合校正合成源的电磁响应异常。

图7为前述四种场源条件下异常体模型与背景模型的电场Ey分量振幅曲线。由图7a可见，单个电偶源条件下，高阻模型与背景模型的电场振幅曲线基本重合，这主要是因为海水层较小，空气波占据电磁信号的主导地位，掩盖了高阻体异常响应。图7b为51个简单合成源(即c1=0，c2=0)产生的水平电场振幅曲线，图7c为经过相位校正后(即c2=0)的合成源归一化振幅曲线，这里参照前述一维模型分析结果，选择c1=0.7。由图7b和图7c可知，采用简单合成源和相位校正合成源时，高阻模型和背景模型的电场归一化振幅相比单源情形有所增强，但是这两种模型的归一化振幅曲线基本重合在一起，并未见明显的分离；图7d为相位和振幅组合校正后合成源的电场归一化振幅曲线，可见高阻体模型与背景模型的电场归一化振幅曲线发生了分离。

图7 四种场源条件下高阻模型和背景模型的电场Ey分量振幅曲线(a)单源； (b)简单合成源； (c)相位校正合成源；(d)相位与振幅综合校正合成源

为了进一步分析合成源的效果，基于图7绘制了四种场源(单源、简单合成源、相位校正合成源及相位与振幅综合校正合成源)的归一化振幅、有效异常和可探测度曲线(图8)。

图8 二维模型单源、简单合成源、相位校正合成源(c1=0.7)、相位与振幅综合校正合成源(c1=0.7，c2=0.2)的归一化振幅R(a)、有效异常S(b)和可探测度D(c)曲线

由图8a可知：单源、简单合成源和相位校正合成源(c1=0.7)三种场源的归一化振幅曲线基本重合，因此这三种源对高阻体的识别能力较弱；相位与振幅组合校正合成源的归一化曲线存在一个明显的负异常，当收发距大于-1km时，归一化振幅随着收发距的增大而减小，当收发距为1.2km时，归一化振幅值达到极小值0.4，然后归一化值开始随着收发距的继续增大而增大，当收发距为5km时归一化振幅基本趋于稳定。由于归一化振幅值小于1，基本无法识别高阻体，因此在浅海区利用归一化振幅识别高阻体具有局限性。

由图8b可知，单源有效异常曲线随着收发距的增大未发生较明显变化，其最大值为0.31。然而，简单合成源、相位校正合成源及相位与振幅组合校正合成源三种场源的有效异常曲线均存在一个明显的正异常，其最大值分别为2.45、4.20和11.4。由此可知，在浅水区，利用有效异常可识别高阻体，且经过相位与振幅组合校正后的合成源有效异常对高阻体的识别能力最强，相位校正合成源的效果次之，单源效果最差。

由图8c可知，简单合成源、相位校正合成源及相位与振幅组合校正合成源的可探测度曲线均存在一个正异常，可探测度值分别为2.5、5.56和12.08。由此可见，在浅海区经过相位与振幅组合校正后的合成源的可探测度参数对高阻体识别能力最强，相位校正源效果次之，单源效果最不理想。

综上可知，无论单源、简单合成源、相位校正合成源还是相位与振幅组合校正合成源，其可探测度对于识别高阻体具有最好的效果，有效异常效果次之，归一化振幅效果最差。

5 三维模型合成源的可探测度

采用如图9所示三维模型。若三维体电阻率为100Ω·m，则代表高阻体模型；若电阻率为1Ω·m，则为背景模型。采用Inline采集模式，51个水平电偶极源(Tx)均沿y方向置于海底上方20m处，范围为-9～-4km，间距为100m，发射频率为0.25Hz。126个接收站(Rx)也沿y方向布置于海底-10～15km的范围内，间距为200m。

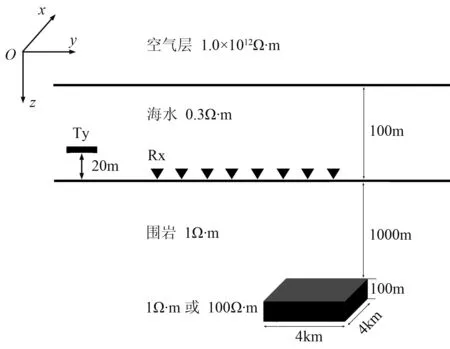
图9 三维海洋模型

分别计算单源、简单合成源及相位与振幅综合校正合成源的三维模型的电场振幅(图10)。图10中两条垂直虚线表示高阻体在y方向的延伸范围。由图10d可见，经相位与振幅综合校正后的合成源可探测度得到明显提高，相比单源情形可探测度异常值提高了约20倍，且异常覆盖的范围大部分位于三维体正上方，为推断异常体横向分布范围提供了依据。总的来说，经过综合校正后的合成源的可探测度利于识别三维异常体。

图10 三维模型单源(a)、简单合成源(b)及相位与振幅综合校正合成源(c)产生的振幅曲线以及三种源场源的可探测度曲线(d)

6 实测数据合成源电磁响应

将上述合成源方法应用于某测区实测MCSEM数据处理。测区海底深度约为770m，高阻储层埋深约为1500m。测区的背景模型根据地质和地球物理资料构建。

图11为实测MCSEM数据电磁响应剖面。由图11a可知，当收发距较小时，背景模型的理论电场振幅曲线与实测曲线基本重合；随着收发距增大，二者逐渐分离，高阻体的影响逐渐凸显；但当收发距大于5km后，实测曲线开始出现振荡，且随着收发距增大，振荡现象更严重，这是数据质量变差所致。

构建一个4.1km长的合成源，相位与振幅综合校正后的合成源的振幅曲线如图11b所示。由图11b可知，当收发距大于5km后，随着收发距的增大，实测数据与背景场的电场振幅曲线逐渐发生分离，分离程度先增大后减小，即电磁异常清晰可见；同时，相比大收发距时实测单源电场振幅曲线的剧烈振荡，实测数据的合成源振幅曲线更光滑。

图11c为可探测度曲线，由图可知，在5～10km范围内，单源的可探测度曲线振荡较剧烈，而合成源的可探测度曲线在该区间平缓变化，即先缓慢增大再逐渐减小，充分说明了合成源具有较好的效果。

图11 实测MCSEM数据电磁响应(a)单源； (b)相位与振幅综合校正后合成源； (c)可探测度曲线

7 结论

本文通过计算海洋一维、二维模型正演电磁响应，探讨了归一化振幅、有效异常和可探测度在浅水区对高阻层的识别能力，结果表明可探测度参数的识别能力最强、有效异常次之、归一化振幅最差。在此基础上，建立海洋三维模型，计算不同源情形下的可探测度，结果表明，相位与振幅综合校正合成源的可探测度对异常指示效果最好，仅相位校正合成源的效果次之，单源识别能力最差。将该方法应用于实际数据处理，经过合成源处理后可探测度能在一定程度上指示高阻异常体的存在。

参考文献

[1] 严波，李予国，韩波等.任意方位电偶源的MCSEM电磁场三维正演.石油地球物理勘探，2017，52(4)：859-868.

Yan Bo，Li Yuguo，Han Bo et al.3D forward modeling of MCSEM electromagnetic field of arbitrary azimuth dipole source.OGP，2017，52(4)：859-868.

[2] 徐凯军，杜润林，刘展.海洋可控源电磁与地震一维联合储层参数反演.石油地球物理勘探，2016，51(1)：197-203.

Xu Kaijun，Du Runlin，Liu Zhan.Inversion of 1D re-servoir parameters of MCSEM and seismic.OGP，2016，51(1)：197-203.

[3] Eidesmo T，Ellingsrud S，Macgregor L M et al.Sea bed logging (SBL)，a new method for remote and direct identification of hydrocarbon filled layers in deepwater areas.First Break，2002，20(2)：144-152.

[4] Constable S.Ten years of marine CSEM for hydrocarbon exploration.Geophysics，2010，75(5)：75A67-75A81.

[5] Constable S，Srnka L J.An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration.Geophysics，2007，72(2)：WA3-WA12.

[6] 何展翔，孙卫斌，孔繁恕等.海洋电磁法.石油地球物理勘探，2006，41(4)：451-457.

He Zhanxiang，Sun Weibin，Kong Fanshu et al.Marine electromagnetic approach.OGP，2006，41(4)：451-457.

[7] 周建美，李貅，戚志鹏.浅水域各向异性地层中的瞬变电磁响应分析.石油地球物理勘探，2016，51(4)：821-830.

Zhou Jianmei，Li Xiu，Qi Zhipeng.Transient electromagnetic response analysis of anisotropic formation in shallow water.OGP，2016，51(4)：821-830.

[8] Andréis D，MacGregor L.Controlled-source electro-magnetic sounding in shallow water：Principles and applications.Geophysics，2008，73(1)：F21-F32.

[9] 殷长春，刘云鹤，翁爱华等.海洋可控源电磁法空气波研究现状及展望.吉林大学学报(地球科学版)，2012，42(5)：1506-1520.

Yin Changchun，Liu Yunhe，Weng Aihua et al.Current status and prospect of marine controlled source electromagnetic airwave.Journal of Jilin University (Earth Science Edition)，2012，42(5)：1506-1520.

[10] Fan Y，Snieder R，Slob E et al.Steering and focusing diffusive fields using synthetic aperture.Epl，2011，95(3)：34006.

[11] Fan Y，Snieder R，Slob E et al.Synthetic aperture controlled source electromagnetics.Geophysical Research Letters，2010，37(13)：69-73.

[12] 汪轩，沈金松.综合合成孔径和径向消除压制浅海可控源电磁勘探中空气波影响.中国地球科学联合学术年会，2014.

Wang Xuan，Shen Jinsong.Apply synthetic aperture and radial elimination method to depress the airwave of controlled source electromagnetic exploration in shallow sea.Joint Academic Annual Meeting of Chinese Geoscience，2014.

[13] Knaak A，Snieder R，Fan Y et al.3D synthetic aperture and steering for controlled-source electromagne-tics.The Leading Edge，2013，32(8)：972-978.

[14] Knaak A.3D synthetic aperture for controlled-source electromagnetics.Geophysics，2015，80(6)：E309-E316.

[15] Yoon D，Zhdanov M S.An optimal synthetic aperture method for the creation of directional sensitivity and removal of the airwave effect in MCSEM data.SEG Technical Program Expanded Abstracts，2014，33：685-690.

[16] Zhdanov M S，Yoon D，Mattsson J.Rapid imaging of towed streamer EM data using the optimal synthetic aperture method.IEEE Geoscience & Remote Sensing Letters，2017，99：1-5.

[17] Constable S，Weiss C J.Mapping thin resistors and hydrocarbons with marine EM methods：Insights from 1D modeling.Geophysics，2006，71(2)：G43-G51.

[18] Mittet R.Normalized amplitude ratios for frequency-domain CSEM in very shallow water.Aesthetic Plastic Surgery，2014，26(11)：47-54.

[19] 裴建新，王启，张秀丽.海洋CSEM探测海底天然气水合物的有效异常研究.石油地球物理勘探，2015，50(1)：177-183.

Pei Jianxin，Wang Qi，Zhang Xiuli.Effective anomaly study of gas hydrate detection using marine CSEM method.OGP，2015，50(1)：177-183.

[20] 赵慧，李予国，刘婷婷.利用可探测度探讨海洋可控源电磁响应的等值性.地球物理学进展，2016，31(2)：928-936.

Zhao Hui，Li Yuguo，Liu Tingting.Study on the equivalence in marine controlled source electromagnetic method using detectivity.Progress in Geophysics，2016，31(2)：928-936.

[21] 刘婷婷，李予国.海洋可控源电磁法对天然气水合物高阻薄层的可探测度.海洋地质前沿，2015，31(6)：17-22.

Liu Tingting，Li Yuguo.Detectivity of gas hydrate high-resistivity layer with marine CSEM method.Marine Geology Frontiers，2015，31(6)：17-22.

[22] 刘颖，李予国.层状各向异性介质中任意取向电偶源的海洋电磁响应.石油地球物理勘探，2015，50(4)：755-765.

Liu Yin，Li Yuguo.Marine electromagnetic response of an arbitrary orientation galvanic source in layered anisotropic medium.OGP，2015，50(4)：755-765.

[23] Li Y G，Li G.Electromagnetic field expressions in the wavenumber domain from both the horizontal and vertical electric dipoles.Journal of Geophysics and Engineering，2016，13(4)：505-515.

[24] 李刚，李予国，韩波等.基于改进的接收点插值算法的频率域海洋可控源电磁法2.5维正演.地球物理学报，2017，60(12)：4887-4900.

Li Gang，Li Yuguo，Han Bo et al.2.5D marine CSEM modeling in the frequency-domain based on an improved interpolation scheme at receiver positions.Chinese Journal of Geophysics，2017，60(12)：4887-4900.

[25] Li G，Li Y G，Han B.Accurate interpolation at recei-ver positions：a novel method for frequency-domain marine CSEM finite-difference modelling.Pure and Applied Geophysics，2017，174(5)：2143-2160.

[26] Fan Y，Snieder R，Slob E et al.Increasing the sensitivity of controlled-source electromagnetics with synthetic aperture.Geophysics，2012，77(2)：E135-E145.