随机边界的波场重建技术研究

程钰纹，罗志鹏

(1. 长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100； 2. 长江大学 地球物理与石油资源学院，湖北 武汉 430100)

0 前 言

地震波逆时偏移法[1]是当前偏移方法中精度很高的一种成像方法，逆时偏移法采用的是全波场波动方程，对波动方程中的微分项采用差分离散(如有限元法、伪谱法、有限差分法等),其对波动方程的近似比较少(这主要由微分与差分方程的逼近程度来决定)，所以其不受偏移孔径和倾角的约束，在处理纵横向上有剧烈变化的地球介质物性特征(如密度、速度等)上很有成效。但是，计算量大和所需存储量高使其无法适用于大数据量的地震成像。利用随机边界波场重建技术，可以最大程度降低计算量和存储量，使得在实际操作过程中可以有效地利用地震波逆时偏移法。因此，对随机边界的波场重建技术的研究就显得格外关键。首先要选择有效的存储方法[2]，加以随机边界条件，用计算量来减小存储量，然而这也使计算成本增加了很多。为了降低宽边界所带来的计算压力，将边界宽度进一步缩小，同时也不能影响随机效果，可以采用不同形式的随机边界函数，以随机介质的散射理论[3]为基点，获得最优散射效果的随机边界构建算法(在有限边界宽度的条件下)。使有限宽随机边界散射性能得到充分发挥，压制相干能量的产生，从而提高逆时偏移计算的效率。因此，研究随机边界波场重建技术对逆时偏移法应用于实践是极其重要的，为往后地震波逆时偏移法的进一步提升打下坚实的基础。

1 常规二阶声波波动方程

以建立波动方程的3个基本方程(应力与应变方程、位移与应力方程和位移与应变方程)为基点，从而推出用压力P和体积模量K为变量的波动方程。

(1)

其中，K为体积模量，K=λ；V是纵波速度；P是声压，ρ是密度。

2 随机边界

2.1 随机边界的建立

以二维各项同性介质[4]的一阶应力—速度声波波动方程为例，以通常的交错网格高阶有限差分法对式(1)进行时间2阶、空间2N阶离散，其反向传播时所用离散差分格式如下：

对于全部的x、y、z，当他们全部在给定的边界区域内，而d(d为边界内的距离)也在给定的边界区域内部的时候，就可以建立随机边界模型。否则将V(x,y,z)加上r*d(r为随机给定的参数)赋给一个中间值，当这个中间值满足边界条件的时候，将其赋值给V(x,y,z)，这样就可以建立随机边界模型[5]。

2.2 基于随机边界的正演模拟

随机边界存储策略一般是在边界上布置一定厚度的随机模型，在边界处给出随机速度，正演存储的是整个模型最后一个时刻的波场值。

设定正演网格区域大小为300 m×300 m，空间网格大小为dx=dz=5 m，dt=0.5 ms，子波主频f=40 Hz，震源位于网格坐标(150 m,150 m)处。模型密度ρ=800 kg/m3，Vp=1 700 m/s。图1为随机边界模型。

3 随机边界正演影响因素

3.1 网格数对随机边界的影响

设定随机边界介质模型网格区域大小为300 m×300 m，空间网格大小dx=dz=5 m，时间间隔dt=0.5 ms，子波主频f=40 Hz，密度ρ=800 kg/m3，Vp=1 700 m/s。震源位于网格坐标(150 m,150 m)处，边界吸收网格数分别为20、40以及60。由下图(图2)中随机边界正演所得到波场快照可以看出(在图2中，I代表网格数)，随着边界吸收网格数的增大，其反射相干能量随之降低。

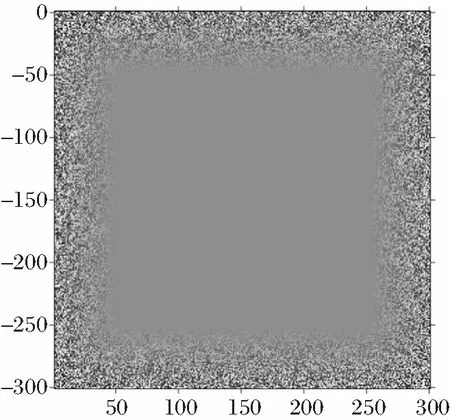
图1 随机边界模型

图2 网格数对随机边界的影响

3.2 子波主频对随机边界的影响

设定随机边界介质模型网格区域大小为300 m×300 m，空间网格大小dx=dz=5 m，时间间隔dt=0.5 ms，密度ρ=800 kg/m3，Vp=1 700 m/s。震源位于模型中间网格(150 m,150 m)处，子波主频分别为10，20，40 Hz。由下图(图3)波场快照可以知道，随着子波主频的增大，反射相干能量随之降低。

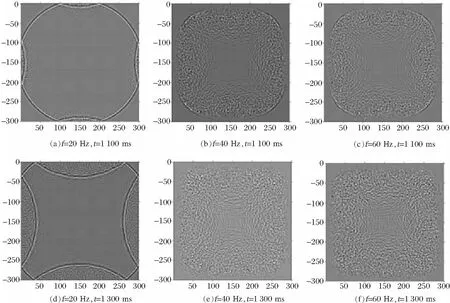
图3 子波主频对随机边界的影响

4 吸收边界和随机边界方法的波场重建

边界介质模型网格区域为300 m×300 m，空间网格大小dx=dz=5 m，时间间隔dt=0.5 ms，密度ρ=800 kg/m3，Vp=1 700 m/s，子波主频f=40 Hz。震源位置位于模型网格(150 m,150 m)处，图4中a是吸收边界介质模型，b是随机边界介质模型。

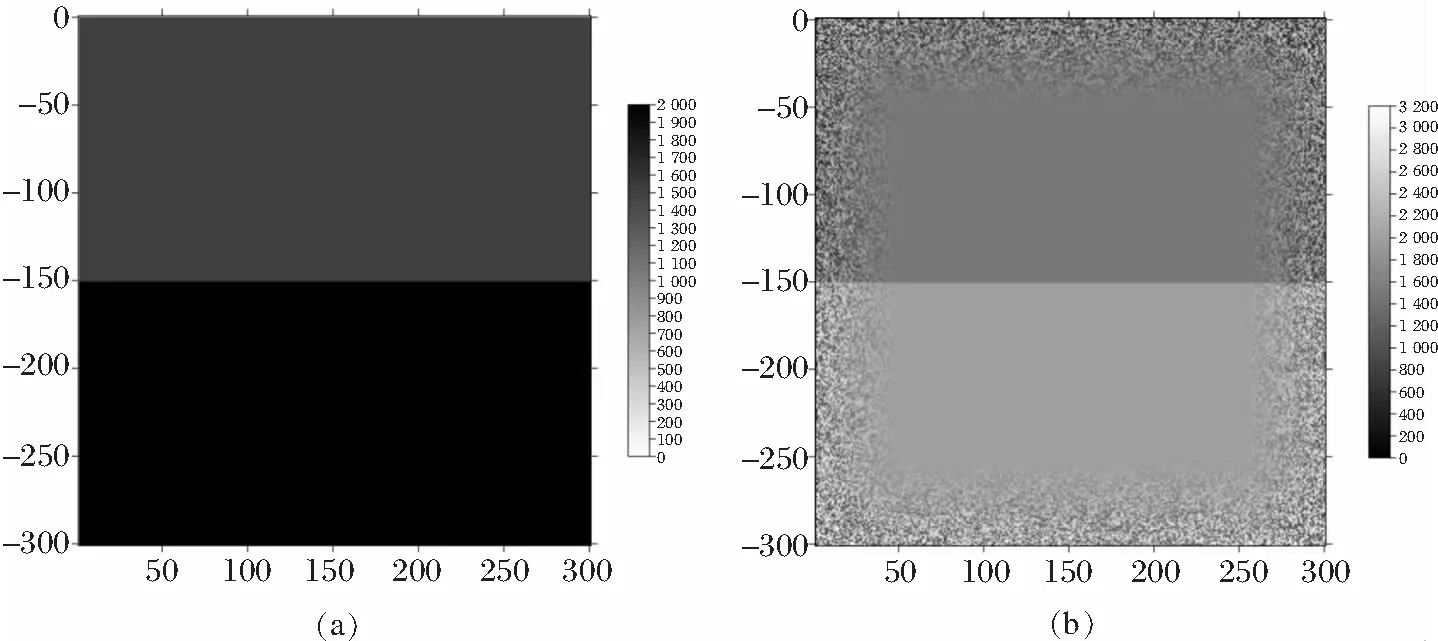
图4 吸收边界和随机边界介质模型

图5为基于随机边界介质模型的正演模拟和波场重建成图以及两者之差。图6为基于吸收边界[6]介质模型的正演模拟和波场重建成图以及两者之差。

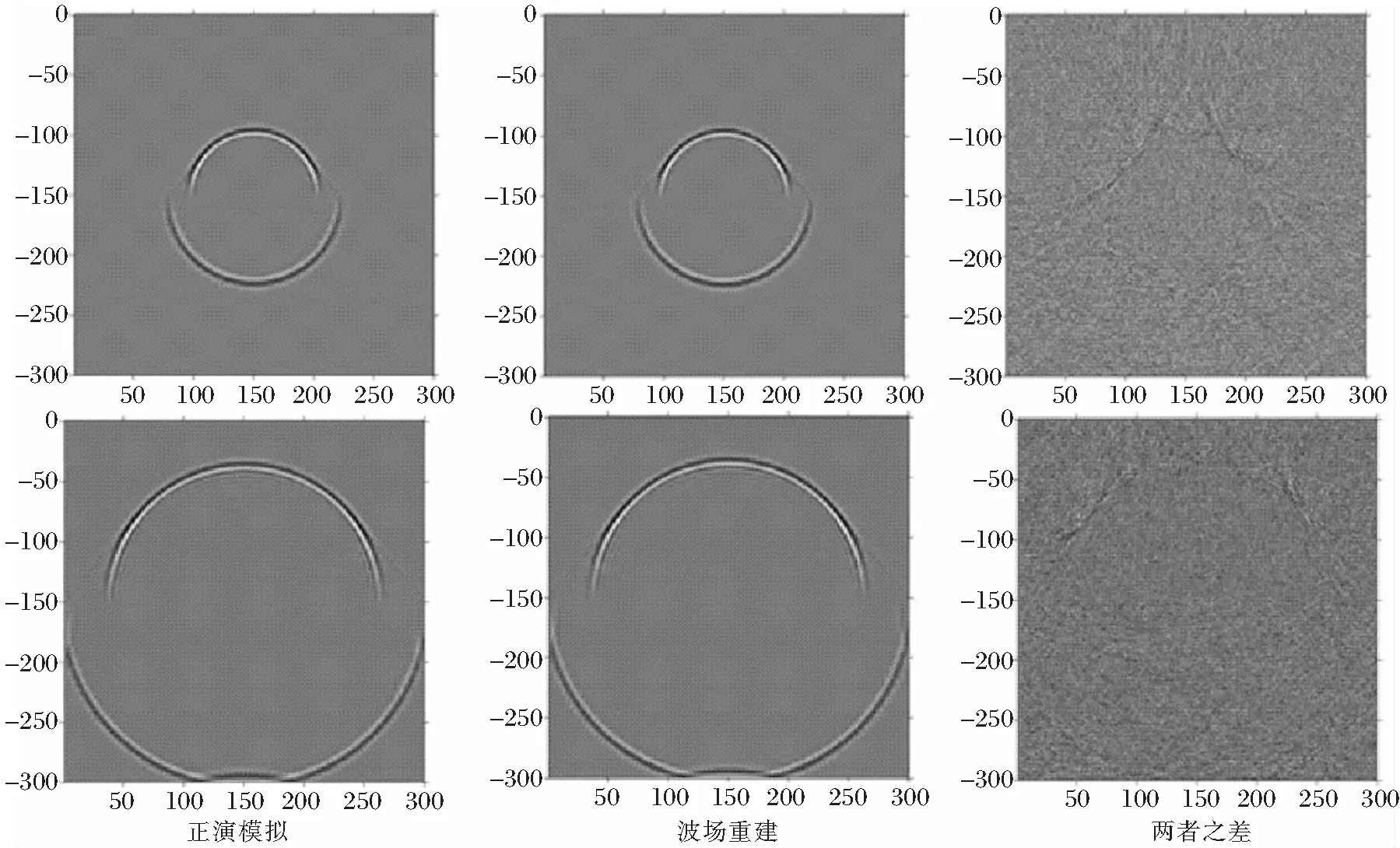
图5 随机边界的正演模拟和波场重建成图及两者之差

图6 吸收边界正演模拟和波场重建成图及两者之差

从上述几张图可以看出，当时间t取值较小的时候，基于随机边界波场重建法以及基于吸收边界波场重建法相差并不大，两种方法效果都比较好。但当时间t取值较大时，随机边界波场重建法明显就要优于吸收边界波场重建法。

5 结 论

1)与正演模拟结果相比，使用随机边界波场重建法和吸收边界波场重建法都可以取得较好的效果。

2)参数的选择是尤为关键的，在差分计算中，不合理的参数很可能会造成模拟结果网格频散严重，对分析模型有很大的影响，甚至会使得数据溢出。

3)在差分精度上，子波的频率越低，网格间距越小，其精度越高。另外，网格间距是影响差分精度的主要原因。

4)在吸收边界的情况下进行波场重建，用吸收边界网格内的数据进行波场重建与正演模拟得到的结果近似。随机边界条件下，波场重建方法可以得到较好的效果。时间取值较大时，随机边界波场重建法要比吸收边界波场重建法效果好。

参考文献：

[1] 杨勤勇, 段心标. 逆时偏移技术发展现状与趋势[J]. 石油物探, 2010, 49(1): 92-98.

[2] 王保利, 高静怀, 陈文超, 等. 地震叠前逆时偏移的有效边界存储策略[J]. 地球物理学报,2012, 55(7): 2412-2421.

[3] 胡明顺, 潘冬明, 董守华, 等. 基于散射理论的逆时偏移随机边界构建策略优化分析[J].地球物理学进展, 2013, 28(4): 2069-2077.

[4] 吴国忱, 秦海旭. 各向同性弹性波随机边界逆时偏移[J]. 地球物理学进展, 2014, 29(4): 1815-1821.

[5] 胡昊, 刘伊克, 常旭, 等. 逆时偏移计算中的边界处理分析及应用[J]. 地球物理学报, 2013, 56(6): 2033-2042.

[6] Higdon R L. Absorbing boundary conditions for elastic wave equation[J]. Geophysics, 1991(56): 231-241.