先进高强钢DP1000地板中央通道的成形回弹及补偿研究
李 贵, 崔赛赛, 陈志平, 龙小裕, 杨 朋, 梁中凯
(1.冶金装备及其控制教育部重点实验室(武汉科技大学), 武汉 430081; 2.机械传动与制造工程湖北省重点实验室(武汉科技大学),武汉 430081;3. 材料成形与模具技术国家重点实验室(华中科技大学),武汉 430074; 4.广东科龙模具有限公司,广东 佛山 528303)
以DP钢和TRIP钢为代表的先进高强度钢板因具有较好的应变均化能力和成形性能,已成为当前汽车轻量化的主要材料[1],如DP1000.但由于其具有非常高的强度,容易产生回弹,回弹规律难以预测[2-3],且强度等级越高,回弹越严重.目前,回弹已成为先进高强度钢板应用的主要瓶颈之一.回弹受诸多因素影响[4],其中材料性能是一个关键因素[5].相比低碳钢,高强度钢板还表现出明显的包辛格效应[6],庄京彪[7]和Sumikawa等[8]通过考虑材料的包辛格效应来提高回弹模拟精度.Wang等[9]用非饱和动态Swift模型(NKS)描述DP980钢板加载过程的材料变形规律,提出了一种惯性释放的回弹计算方法来提高其预测精度.Yang[10]等考虑杨氏模量的变化,采用分段硬化函数预测板料折弯回弹.工艺参数也是回弹的重要影响因素,Neto等[11]分别采用1/2、1/4对称和全板料3种方式对回弹进行模拟,结果表明采用全板料可以获得更精确结果,对于回弹应采用全板料进行模拟.徐刚等[12]通过伺服压机对成形速度和载荷的精确控制来减少弯曲回弹.上述方法在一定程度上虽然可以减少回弹,但尚不能完全消除,回弹补偿仍是目前解决回弹问题的最有效方法[13],其本质是基于回弹预测结果对模具型面进行几何逆向补偿[14-16].如何实现回弹补偿的一次成功,减少补偿次数,是一个面向冲压成形领域的重要工程问题.
本文以某汽车地板中央通道零件为对象,研究DP1000钢板的冲压成形及回弹特性.从工艺方案优化设计、数值模拟、型面几何补偿等对回弹进行精确预测和控制.基于数值模拟和几何特征的全工序回弹补偿,实现回弹的精确控制.并基于补偿后的模具型面进行冲压实验,验证该回弹补偿的有效性和可靠性,以期为其他同类型先进高强度钢板零件回弹的解决提供参考依据.
1 工艺方案优化设计
图1所示为某汽车地板中央通道零件图.该零件最大外形尺寸为996.0 mm×536.2 mm,属于中大型零件.材质为瑞典SSAB公司生产的DP1000钢板,厚度0.9 mm.根据截面视图分析,零件类似于3个几字型形状上下对接而成,比一般U型零件复杂.零件侧面还有两个内凹鼓包,且图示B区域并非完全对称,增加了回弹预测的难度.
该零件的变形主要是圆角区域的弯曲,结合其几何形状分析,回弹是最主要问题.侧面的两个鼓包成形时可能会开裂,其他区域不会出现开裂、起皱缺陷.因图1中所示零件的非对称B区域产品边界复杂,正常修边困难,故采用落料工序以避免后续修边.而成形工艺方案可分为几字型弯曲成形和两侧鼓包成形.图2所示冲压方向下,两侧鼓包存在冲压负角,需在几字型成形后,利用斜楔进行侧向整形,是一个局部胀形过程,鼓包周围的材料会朝鼓包内流动,使侧壁面产生弹性能和应力分布不均而造成回弹扭曲.因此,前工序设计成外凸鼓包储料,消除侧壁面的扭曲变形.
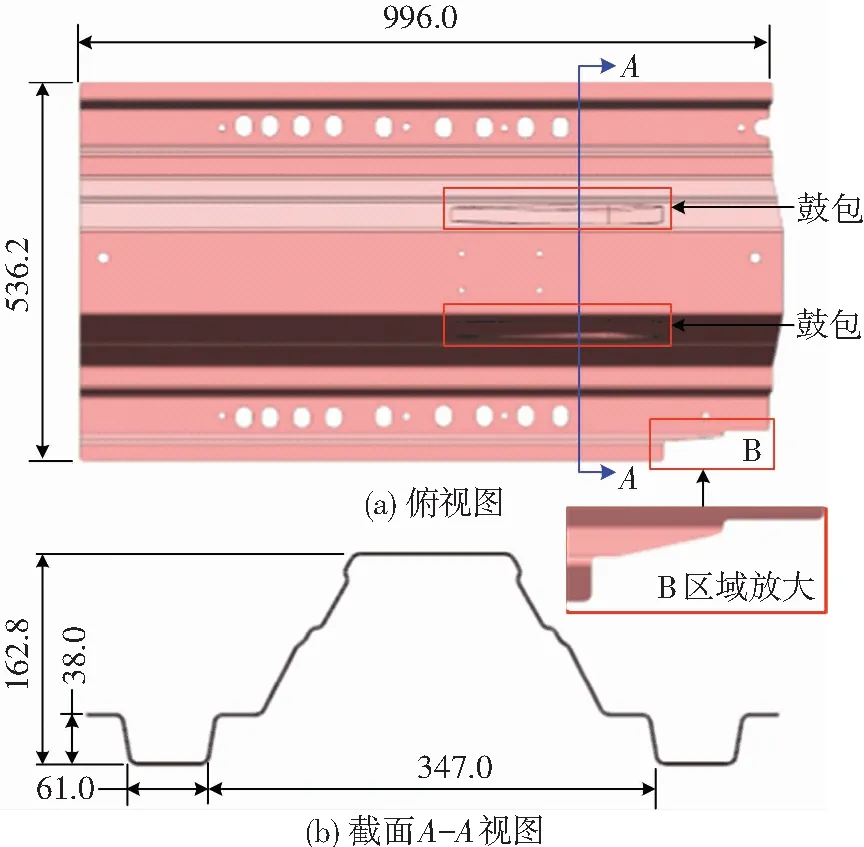
图1 地板中央通道零件图
Fig.1 Part drawing of floor panel tunnel: (a) top view; (b) section viewA-A
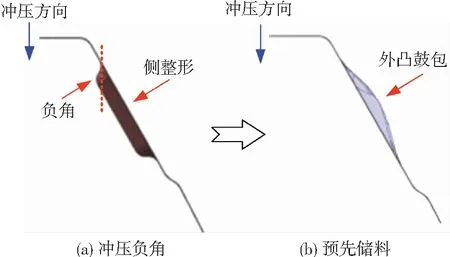
图2 鼓包处成形方案
Fig.2 Forming of convex hulls: (a) stamping undercut; (b) storing sheet material
该零件的几字型成形方案主要有3种,如图3所示.方案1为3次成形组成,第1次拉深成形中间几字型,两侧倒几字型分别通过两次翻边成形.方案2缩减为两次成形组成,中间几字型与两侧倒几字型的一半合并组成带有台阶的大几字型形状一并拉深成形,其二次翻边与方案1中3次翻边一致.而方案3则只需要1次成形.根据最少工序数原则,以及后续回弹解决的可行性分析,方案2相对最优,且带有台阶的拉深可以减少回弹.
采用方案2时,一次拉深时需将图2(b)所示的外凸储料鼓包一并成形.模具结构的截面简图如图4所示.几字型的顶部通过压料块压紧,凹模下行将板料压至下死点,使其与凸凹模完全贴膜.可以预见,两侧台阶和圆角区会产生严重回弹,为了便于回弹的补偿和调整,将该区域设计成独立镶块.二次翻边是常规的上翻边成形,此处不再赘述.因此,该零件最终的工艺优化设计方案如图5所示,其中两次成形工序的回弹是该零件的关键问题.
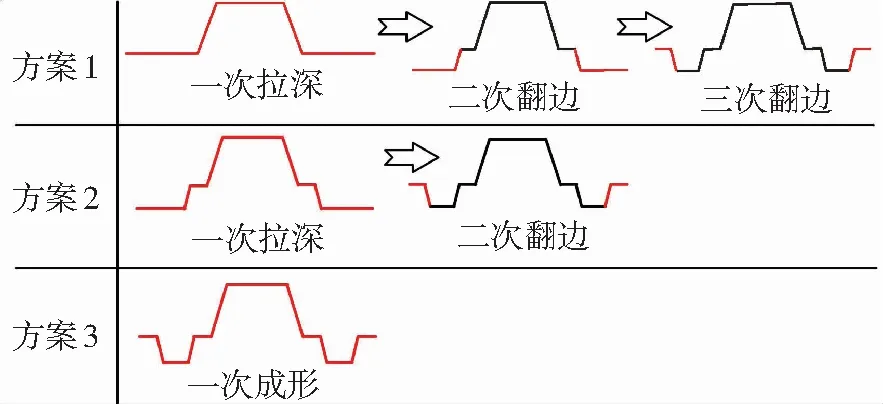
图3 成形方案比较
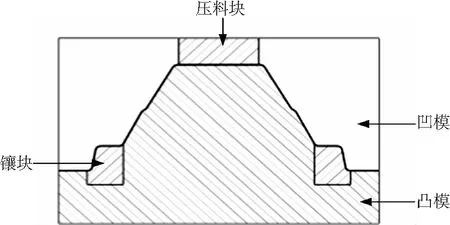
图4 一次拉深模具结构截面简图

图5 地板中央通道冲压工艺方案
2 回弹模拟与实验结果
基于优化的工艺设计方案,研究DP1000钢板的地板中央通道的冲压回弹及其补偿特性,着重分析一次拉深、二次翻边的回弹及其补偿规律.本文采用Z050电子万能材料试验机对板料试样进行单向拉伸试验,最大实验力为50 kN,配备纵横向引伸计测量各向异性参数.详细测量数据如表1所示.以Autoform R6为回弹数值模拟的分析软件,摩擦系数设置为0.15.

表1 DP1000钢板力学性能参数
采用壳单元分别对一次拉深和二次翻边进行成形和回弹模拟,厚向积分点为11个.回弹模拟结果如图6所示,两侧法兰朝外侧翘曲严重.一次拉深的最大回弹为26.6 mm,二次翻边后的最大回弹为31.1 mm,可见DP1000的回弹变形非常严重.

图6 成形回弹模拟结果
Fig.6 Springback simulation results of forming: (a) springback of the first drawing; (b) springback of the second flanging
基于上述工艺方案进行模具设计与制造,所有工作部件均设计成镶块结构,为回弹补偿预留足够的型面整改余量.图7是未进行任何型面补偿的回弹实验结果,两侧法兰翘曲严重,斜面侧壁存在严重的“花盆”现象.图7(a)中左右两处测量值分别为10 和18 mm;图7(b)中左右两处测量值分别为7和24 mm.因二次翻边的法兰变形对已成形台阶有补偿作用,故回弹值相应减少.

图7 弯曲回弹实验结果
Fig.7 Springback experiment results of bending: (a) experimental results of springback of the first drawing; (b) experimental results of springback of the second flanging
因回弹结果成对称分布,故此处只取其中一半进行分析.以坐标原点为起始点,沿X正向等间距取9个测量点的回弹值进行定量分析,结果如表2所示.根据结果分析可知,第2次翻边最大回弹量达到36.27 mm.第1次拉深回弹的模拟值与实验值比较接近,偏差在1~2 mm,但二次翻边回弹误差有所增加,最大为3.17 mm.可见,数值模拟可以预测回弹趋势,且回弹结果与实际比较接近,可用于指导回弹补偿.但随着成形工序的增加,工艺越复杂,回弹的模拟精度会降低.

表2 回弹模拟及实验结果对比
3 全工序几何回弹补偿
根据上述的回弹模拟和实验结果对比分析可知,DP1000的先进高强度钢板会产生严重的回弹缺陷,已严重影响到零件的尺寸精度.回弹补偿是解决回弹问题的最佳方法,而冲压成形的每一个工序都可能存在尺寸和精度损失,如果累积到最后工序再进行回弹补偿会导致极大的误差.而对于回弹比较复杂的零件,最后工序回弹补偿也难以将回弹完全消除,中间工序的模面也不可控制,存在较大风险.因此,文章采用全工序回弹补偿,每一道工序都进行回弹的独自补偿,直至达到型面及尺寸要求,即回弹的自工序完结.
根据前述回弹模拟及实验结果对模面进行几何逆向补偿.图8是两次成形的模面补偿前后截面示意图.第1次拉深的型面补偿最大为26 mm,第2次翻边的型面最大补偿量达到14.4 mm.两次回弹补偿叠加达到40.4 mm.因该零件的回弹主要由圆角处的弯曲变形所导致,故通过在圆角几何位置逆向折入角度的方式进行补偿.但该零件除了弯圆角区域以外,圆角与圆角之间的连接面(基本都是平面)是由初始板料流过弯曲圆角而成形,没有达到塑性屈服,存在较大的弹性能,卸载之后会出现内凹的“花盆式回弹”.因此,平面位置需做折入回弹补偿,折入点用大圆角光滑过渡,补偿后的型面在“花盆”最严重的位置呈现外凸形状.图8(a)中有两个“花盆”折入点,分别折入9°和4°.而图8(b)中两个斜面的“花盆”折入角度均为10°.同时还将容易产生变形的弯曲圆角缩小,即减小相对弯曲半径,增加圆角处的塑性变形.
按照补偿的模面对模具进行加工调试,得到第1次回弹补偿后的零件,如图9所示.通过圆角处和斜面的折入补偿,“花盆”基本被校平,外侧法兰回弹得到了有效控制,但还存在3 mm左右的回弹.
为了进一步消除外侧法兰回弹,需进行进第2次回弹补偿.将第1次拉深的顶端由平面更改为曲面,最大落差为3.3 mm,如图10所示.成形后顶端基本没有曲面痕迹,且消除了两侧法兰的超差,回弹得到了完全控制,如图11所示.
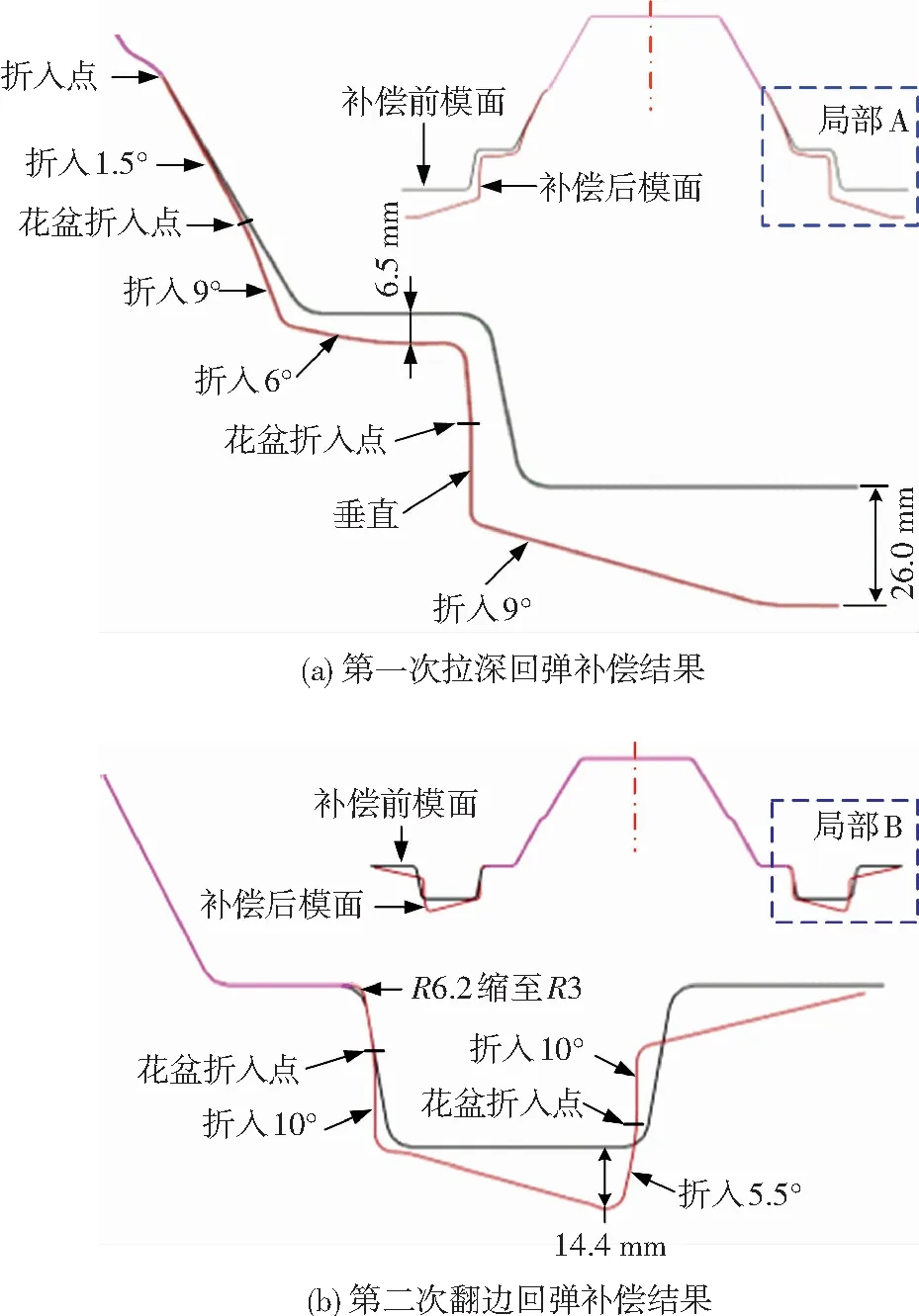
图8 回弹几何补偿截面示意图
Fig.8 Section of geometric compensation: (a) springback compensation of the first drawing; (b) springback compensation of the second flanging

图9 第一次回弹补偿后冲压件
Fig.9 Stamping part after the first compensation:(a) stamping part after springback compensation of the first drawing; (b) stamping part after springback compensation of the second flanging
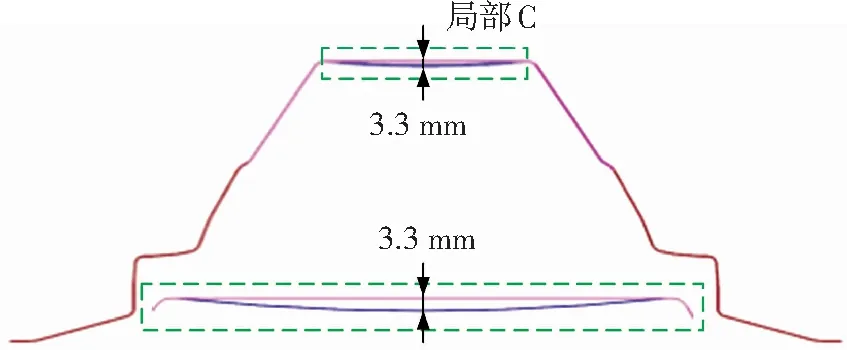
图10 第二次回弹补偿

图11 第二次回弹补偿后冲压件
分别完成侧整形和最后的修边工序,得到最终的冲压零件.将其放置在检具上并采用三坐标测量仪对零件型面误差进行测量.图12是零件两端型面的检测结果.图13是测量组M1的型面超差分析.
表3是图12中测量组M1中的测量点坐标及其偏差数据详细分析.除了测量点M1-MS-2误差为-0.83 mm外,其余测量点全部合格.
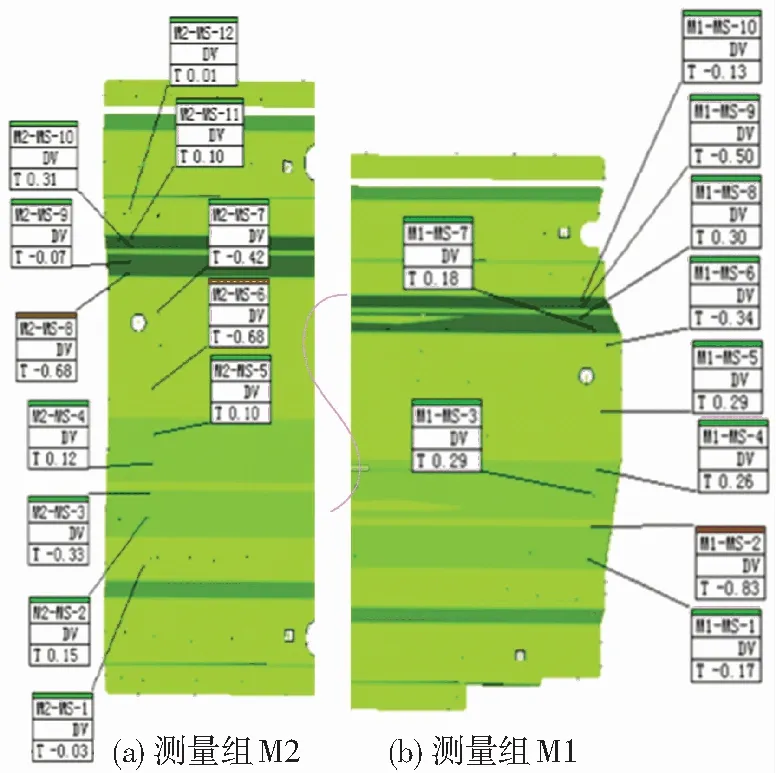
图12 检具测量结果
Fig.12 Measurement results of checking fixture: (a) measurement group M2; (b) measurement group M1

图13 型面测量超差分析
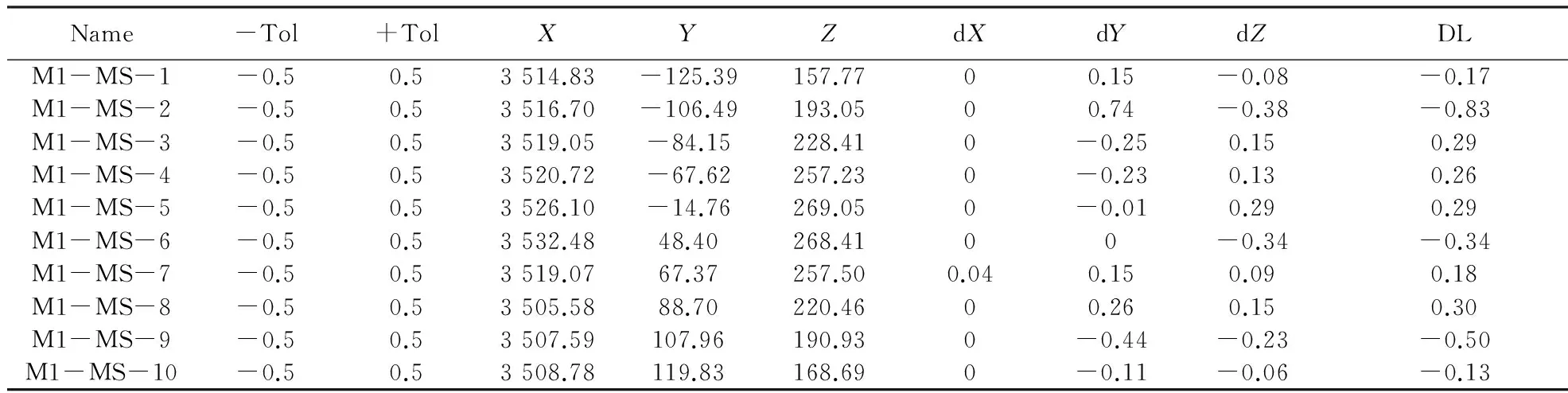
Name-Tol+TolXYZdXdYdZDLM1-MS-1-0.50.53514.83-125.39157.7700.15-0.08-0.17M1-MS-2-0.50.53516.70-106.49193.0500.74-0.38-0.83M1-MS-3-0.50.53519.05-84.15228.410-0.250.150.29M1-MS-4-0.50.53520.72-67.62257.230-0.230.130.26M1-MS-5-0.50.53526.10-14.76269.050-0.010.290.29M1-MS-6-0.50.53532.4848.40268.4100-0.34-0.34M1-MS-7-0.50.53519.0767.37257.500.040.150.090.18M1-MS-8-0.50.53505.5888.70220.4600.260.150.30M1-MS-9-0.50.53507.59107.96190.930-0.44-0.23-0.50M1-MS-10-0.50.53508.78119.83168.690-0.11-0.06-0.13
4 结 论
1)先进高强度钢板DP1000的冲压回弹明显,该零件的两次回弹量叠加后达到了34.27 mm,致使冲压件的尺寸精度严重超差,是成形的主要缺陷.
2)数值模拟可以预测回弹的基本趋势,且回弹结果与实际比较接近,可用于指导回弹补偿.但多次弯曲后,回弹模拟精度降低.因此,对于高强度钢板类零件应减少成形工序,优化工艺方案设计,尽量实现一次成形.
3)回弹补偿是目前处理回弹的最佳方法,结合几何及其回弹模拟和实验结果对型面进行几何补偿,该零件的回弹由最初的最大34.27 mm减少到3 mm,使回弹得到了有效控制.通过第2次对局部型面的补偿即将回弹完全消除.
4)对于这类几字型零件,圆角和侧壁面的折入处理是控制回弹的关键.另外,结构设计时应为回弹补偿预留充分的补偿余量,并与数值模拟相结合,合理采用镶块结构,优化结构设计.
参考文献:
[1] 李贵,柳玉起,柯俊逸, 等. 先进高强度钢板DP590回弹试验及数值模拟研究[J]. 锻压技术, 2013,38(5): 50-55.
LI Gui, LIU Yuqi, KE Junyi, et al. Experimental research and numerical simulation of springback for advanced high-strength steel-DP590 [J]. Forging & Stamping Technology, 2013, 38(5): 50-55.
DOI:10.3969/j.issn.1000-3940.2013.05.011
[2] CHENG G, CHOI K S, HU X, et al. Predicting deformation limits of dual-phase steels under complex loading paths[J]. JOM, 2017, 69(6): 1046-1051.
DOI: 10.1007/s11837-017-2333 -7
[3] LEE E M, SHIM D S, SON J Y, et al. Study on design of progressive dies for manufacture of automobile structural member using DP980 advanced high strength steel[J]. Journal of Mechanical Science & Technology, 2016, 30(2):853-864.
DOI:10.1007/s12206-016-0140-7
[4] 刘伟, 刘红生, 邢忠文,等. 高强钢板冲压成形的回弹规律与工艺参数研究[J]. 材料科学与工艺, 2010, 18(6):758- 761.
LIU Wei, LIUHongsheng, XING Zhongwen, et al. Study on process parameters and springback rule for stamping of high strength steel sheet [J]. Materials Science and Technology, 2010, 18(6):758-761.
DOI: 10.11951/j.issn.1005-0299.20100604
[5] CHOI J, LEE J, BAE G, et al. Evaluation of springback for DP980 S rail using anisotropic hardening models[J]. JOM, 2016, 68(7):1850-1857.
DOI: 10.1007/s11837-016-1924-z
[6] HAN K, TYNE C J V, LEVY B S. Effect of strain and strain rate on the bauschinger effect response of three different steels[J]. Metallurgical and Materials Transactions A, 2005, 36(9):2379-2384.
DOI: 10.1007/s11661-005-0110-7
[7] 庄京彪, 刘迪辉, 李光耀. 基于包辛格效应的回弹仿真分析[J]. 机械工程学报, 2013, 49(22):84-90.
ZHUANG Jingbiao, LIU Dihui, LI Guangyao. Analysis of springback simulation based on bauschinger effect [J]. Journal of Mechanical Engineering, 2013, 49(22):84-90.
DOI: 10.3901/JME.2013.22.084
[8] SUMIKAWA S, ISHIWATARI A, HIRAMOTO J, et al. Improvement of springback prediction accuracy using material model considering elastoplastic anisotropy and bauschinger effect [J]. Journal of Materials Processing Technology, 2016, 230(645):1-7.
DOI: 10.1016/j.jmatprotec.2015.11.004
[9] WANG Z, HU Q, YAN J, et al. Springback prediction and compensation for the third generation of UHSS stamping based on a new kinematic hardening model and inertia relief approach [J]. International Journal of Advanced Manufacturing Technology, 2017, 90(1):875-885.
DOI: 10.1007/s00170-016- 9439-x
[10] YANG X, CHOI C, SEVER N K, et al. Prediction of springback in air-bending of advanced high strength steel (DP780) considering Young’s modulus variation and with a piecewise hardening function[J]. International Journal of Mechanical Sciences, 2016, 105(1-2):266-272.
DOI: 10.1016/j. ijmecsci.2015.11.028
[11] NETO D M, OLIVEIRA M C, SANTOS A D, et al. Influence of boundary conditions on the prediction of springback and wrinkling in sheet metal forming [J]. International Journal of Mechanical Sciences, 2017, 122:244-254.
DOI: 10.1016/j.ijmecsci.2017.01.037
[12] 徐刚, 李建军, 付秀娟. 成形速度及载荷对高强钢板回弹影响的研究[J]. 锻压技术, 2012, 37(2):15-20.
XU Gang, LI Jianjun, FU Xiujuan. Research on influence of forming speed and load on springback for high strength steel sheets [J]. Forging & Stamping Technology, 2012, 37(2):15-20.
DOI: 10.3969/j.issn.1000-3940.2012.02.004
[13] LI G, LIU Y, Du T, et al. Algorithm research and system development on geometrical springback compensation system of advanced high strength steel parts [J]. International Journal of Advanced Manufacturing Technology, 2014, 70(1-4): 413-427.
DOI: 10.1007/s00170-013-5230-4
[14] 谢晖, 潘志红, 蒋浩民,等. 高强钢板冲压位移回弹补偿技术研究与应用[J]. 塑性工程学报, 2012, 19(5):72-77.
XIE Hui, PAN Zhihong, JIANG Haomin, et al. Research on springback compensation based on fully cycle simulation of high strength steel [J]. Journal of Plasticity Engineering, 2012, 19(5):72-77.
DOI: 10.3969/j.issn.1007-2012.2012.05.013
[15] 辛秀敏, 路平, 江开勇,等. 基于逆向工程技术的反求因子回弹补偿法[J]. 计算机集成制造系统, 2015, 21(6):1436- 1441.
XIN Xiumin, LU Ping, JIANG Kaiyong, et al. Reversing factor springback compensation method based on reverse engineering technology [J]. Computer Integrated Manufacturing Systems, 2015, 21(6):1436-1441.
DOI: 10.13196/j.cims.2015.06.004
[16] 刘晓晶, 葛希军, 刘朋会,等. 汽车中央通道冲压回弹及其补偿研究[J]. 材料科学与工艺, 2015, 23(4):36-41.
LIU Xiaojin, GE Xijun, LIU Penghui, et al. Stamping springback and springback compensation of the automobile central channel [J]. Materials Science and Technology, 2015, 23(4):36-41.
DOI: 10.11951/j.issn.1005-0299.20150406

