可获知偶发拥堵持续时间的动态车辆路径问题*

李嫚嫚 陆 建▲ 郭文倩

(1.东南大学城市智能交通江苏省重点实验室 南京 210096；2东南大学现代城市交通技术江苏高校协同创新中心 南京 210096；3. 东南大学交通学院 南京 210096；4.大连海事大学交通运输管理学院 辽宁大连 110026)

0 引 言

车辆路径问题(vehicle routing problem, VRP)是物流系统规划战术层和运营层都涉及的重要的组合优化问题[1]。随着信息科技的高速发展，实时通信的实现，动态车辆路径问题逐渐成为了研究热点，尤其，动态行驶时间车辆路径问题[2-5]。

动态行驶时间车辆路径问题的研究最初集中于路段行驶时间受常发拥堵因素(如上下班高峰等)影响的伪动态行驶时间问题，即时变更车辆路径问题，此类问题中的路段行驶时间信息不随时间更新。Malandaraki[6]，Ichoua[7]，Ghiani[8]等对此问题进行了研究，他们逐步建立了满足“先进先出”规则的受常发拥堵因素影响的路段行驶时间函数。由于只考虑常发拥堵因素对路段行驶时间的影响不完全符合真实的交通情况，于是，学者们开始研究路段行驶时间也受偶发拥堵因素(如事故、恶劣天气)影响的真正的动态行驶时间车辆路径问题。此类问题中的路段行驶时间信息会不断被更新。因此，研究重点在于如何根据新获知信息调整车辆配送路径。Potvin等[9-10]探讨了不同信息获知方式下车辆配送路径的调整方法；Taniguchi等[11]、Okhrin等[12]和李妍峰等[3-4]分别探讨了在客户点处、以固定间隔、在关键点处更新客户点间行驶时间调整车辆配送路径的方法及效益。但以上研究基本都假设实时获知的交通信息为受偶发拥堵因素影响的路段行驶时间，未考虑偶发拥堵持续时间也可获知。现有智能交通系统已实现了偶发拥堵持续时间的高精度预测[13]。因而，研究该情形下的动态车辆路径问题更具有实际意义。

笔者针对可获知偶发拥堵持续时间的动态车辆路径问题进行研究，在对问题描述的基础上，提出了根据常发拥堵信息安排车辆初始配送路径，以实时获知的偶发拥堵信息更新车辆配送路径，通过车载导航系统实时指导车辆行驶路线的求解策略，并通过数值算例对该问题进行了模拟分析。

1 问题描述及数学模型

可获知偶发拥堵持续时间的车辆路径问题可描述如下：1个配送中心拥有若干辆车，各车额定载重量不尽相同；它们需在满足车辆载重量约束下以最短总行驶时间完成所有客户的运输服务；每个客户的运输服务类型或为送货或为取货，需求量大于0，小于最小车辆的额定载重量；客户的服务时间为0；路段行驶时间受常发拥堵因素和偶发拥堵因素共同影响；在配送中心开始服务前，所有客户、车辆信息，以及常发拥堵因素影响下的路段行驶时间信息均已获知；受偶发拥堵因素影响的路段行驶时间和其持续时间只能在车辆配送过程中实时获知。

在真实的交通网络中安排车辆配送路径，需首先将路段行驶时间转化为车辆路径问题的直接输入信息——客户点间的行驶时间。笔者采用文献[14]的方法，通过每隔15 min求解1次时变最短路问题实现此目的[14]。在开始配送前，以此方法获得整个配送期间客户点间最短行驶时间，见图1；在配送过程中，以此方法更新偶发拥堵持续期间的客户点间最短行驶时间，见图2；对于某一时刻点的最短行驶时间，以插值法得到。

图1 常发拥堵下的客户点间行驶时间

图2 更新的客户点间行驶时间

为了避免偶发拥堵因素造成车辆总配送时间的显著增加，在获知其信息后，应立即对车辆配送路线进行更新，因此，整个配送期间，车辆的配送路线一直在动态变化。这个调整过程总体上分为：配送开始前，初始车辆配送路线的安排；配送过程中，车辆配送路线的不断更新。在更新车辆配送路线时，由于车辆已离开配送中心，尚未服务送货客户的货物已装载于相应配送车辆，因此，在调整车辆配送路径时，只能调整其被服务的顺序。

在每次更新车辆配送路径时，已使用车辆的位置被设定在车辆将到达的最邻近交叉口，见图3。

图3 车辆位置更新

依据文献[15]，构建数学模型。

针对车辆路径安排时刻t0。

已知数据集合如下。

C为客户点集合(CL∪PK∪DL∪VDC)，其包含4个子集：CL为已使用车辆当前位置子集；PK为尚未服务取货客户子集；DL为尚未服务送货客户子集；VDC由已使用车辆对应虚拟配送中心子集SVDC和未使用车辆对应虚拟配送中心子集UVDC组成。尚未服务取货客户和送货客户子集i∈(PK∪DL)有需求量属性(qi)，配送客户需求量为正值，取货客户需求量为负值；已使用车辆当前位置子集、未使用车辆对应虚拟配送中心子集以及尚未服务送货客户子集i∈(CL∪UVDC∪DL)有服务车辆属性(CTVi)；已使用车辆当前位置子集以及未使用车辆i∈CL还有服务开始时间属性(sti)。

K为车辆集合；其具有额定载重量属性Qk,k∈K；车辆现有载重量属性CQk,k∈K。

M为无穷大的数。

决策变量如下。

i∈(CL∪SVDC∪PK∪DL),

j∈(VDC∪PK∪DL);

i∈(CL∪VDC∪PK∪DL)，k∈K；

wi为车辆离开i客户时的载重量，

i∈(CL∪UVDC∪PK∪DL)；

(1)

客户服务约束见式(2)～(3)。

∀i∈(CL∪UVDC∪PK∪DL)

(2)

(3)

路径约束计算见式(4)～(8)。

∀i∈(CL∪UVDC)

(4)

(5)

(6)

∀j∈(PK∪DL)

(7)

(8)

到达客户点的时间计算见式(9)。

(9)

载重量约束计算见式(10)～(13)。

∀i∈CL

(10)

(11)

(12)

i∈(CL∪UVDC∪PK∪DL)

(13)

两变量之间的关系计算见式(14)。

∀i∈(CL∪UVDC∪PK∪DL);

j∈(PK∪DL∪VDC)

(14)

2 求解算法

问题的总求解流程见图4。

图4 求解流程图

配送开始前，首先求解时变最短路问题获得常发拥堵下各分割点的客户间最短行驶时间；在此基础上，根据已知信息——全部客户、车辆信息以及常发拥堵下各客户(配送中心)间最短行驶时间求解时变取送一体化车辆路径问题安排车辆初始配送路径；配送过程中，由于车辆已离开配送中心，尚未服务送货客户的货物已装载于相应配送车辆，因此，在调整车辆配送路径时，只能调整其被服务的顺序。于是，通过求解特殊时变取送一体化车辆路径问题更新车辆配送路径。每当配送中心通知车辆下1个服务客户后，由车辆自带的导航系统获得其行驶路线，也就是再次求解时变最短路问题。因此，文中所研究问题需求解3个子问题：时变最短路问题；时变取送一体化车辆路径问题以及特殊时变取送一体化车辆路径问题。对其笔者分别采用改进的Dijkstra算法、遗传算法以及2-opt+insertion进行求解。

2.1 改进的Dijkstra算法

路段行驶时间满足“先进先出”规则的时变最短路问题，与标准最短路问题唯一的不同是：为了获得某一时刻路段行驶时间Tij(t)，需获知车辆到达该路段前节点i的时刻ti。因此，经典的最短路问题求解算法——Dijkstra算法，只需将其临时标号更新方法修改为：Tj=Ti+Tij(Ti+t0)，其中，Ti、Tj分别为车辆从出发点到达节点i、j所需行驶时间；Tij(t)为路段(i,j)的行驶时间函数；t0为车辆出发时刻，便能用于求解时变最短路问题。此算法被称为改进的Dijkstra算法，其具体求解过程如下。

步骤1。令t=t0；初始化固定标号集合和临时标号集合为Pi=[0,0]，Ti=[inf;0;inf],∀i∈{1,2,…,NN}。

步骤2。修改起点i的Pi和Ti分别为：Pi=[0;0]，Ti=[0,1,0]；令k=i。

步骤3。判断k是否为终点，不是，转步骤4；否则，转步骤6。

步骤4。更新与节点k相邻且Tj(2)=0节点j的Tj为

步骤5。当i节点的Ti(2)=0且Ti(1)最小时，更新k=i，Ti(2)=1，Pi=[Ti(1),Ti(3)]；转步骤3。

步骤6。输出Pk(1)。

2.2 遗传算法

众多学者曾将遗传算法用于求解车辆路径问题，结果表明遗传算法能获得高质量的解[3,12,15-16]。因此，笔者也选用遗传算法作为时变取送一体化车辆路径问题的求解算法。其中，遗传算法的编码采用随机密钥法[17]、交叉算子为两点交叉、变异算子为均匀变异、选择策略结合了精英策略与轮盘赌法、采用抛弃法处理载重量约束，详细细节请参阅文献[15]。

2.3 2-opt +insertion

针对配送过程的特殊时变取送一体化车辆路径问题，由于其求解结果需实时指导车辆行驶，因此，将传统启发式算法用于求解特殊取送一体化车辆路径问题。对于送货客户，由于只能调整其由车辆服务的顺序，相当于求解1个特殊旅行商问题，同时，初始车辆配送路径可视为1个初始可行解。因此，将旅行商问题的2-opt启发算法用于调整送货客户的服务顺序[2,18]；对于取货客户，其不仅可被重新分配于不同车辆，也能调整其服务顺序，因此，将其分别视为新客户，以车辆路径问题的构筑式启发算法——insertion法——将其重构入当前的解[18]。2-opt+insertion启发式算法的求解时间复杂度为O(n2)，详细步骤如下。

步骤1。将已去除服务客户的初始解中每辆车尚未服务的取货客户去除，并按顺序建立未服务取货客户集PK。

步骤2。以减少车辆行驶时间为目标，用2-opt启发式算法调整每辆车的客户服务顺序。

步骤3。判断PK是否为空集。否，转步骤4；是，转步骤6。

步骤4。按顺序从PK中取出1个取货客户。

步骤5。在满足车辆载重量约束下，以最小行驶时间增加，向配送路径插入取货客户，转步骤3。

步骤6。结束。

3 数值实验

3.1 模拟方法

笔者采用1个10×10网络进行数值模拟。该网络有100个节点，180条路段，每条路段为双向通行，双向自由流行驶时间都为12 min。配送中心拥有3辆车，额定载重量分别为7,8,8 t；需完成10个客户的取送货服务，客户7和客户10为取货客户，其余为送货客户[19]；各客户位置与需求量见图5。

图5 测试网络及客户情况

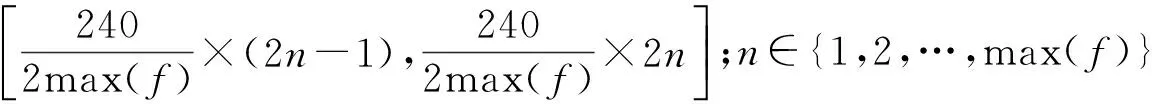
偶发拥堵因素引起的网络变动除与发生频率f，受影响路段行驶时间增加量σ有关外，还与同一刻受其影响的路段数m有关。模拟的受影响路段通过随机选择不重复的路段前、后节点选出。

3.2 数值结果

3.2.1 求解结果

在Matlab中将改进的Dijkstra算法、遗传算法以及2-opt+insertion启发式算法编程实现。以表1参数，运行遗传算法10次，求解得到居于中位的初始车辆配送路径见图6，车辆总行驶时间为864 min。

表1 遗传算法参数表

图6 初始车辆配送路线图

当偶发拥堵因素干扰频率f=8，路段行驶时间变化量σ=11，受偶发拥堵因素影响的路段数m=20时，一次模拟结果见图7，车辆总行驶时间为870.42 min，比按初始配送路线行驶所需时间减少24.38 min。表明笔者所用方法可根据偶发拥堵信息调整车辆配送路线避开受偶发拥堵因素影响路段，减少车辆总行驶时间。

3.2.2 对比分析

为了验证获知偶发拥堵持续时间信息所带来的效益，将根据其调整车辆配送路线(机制3)的效益与不更新车辆配送路线(机制1)的效益和只根据偶发拥堵因素影响下的路段行驶时间信息调整车辆配送路线(机制2)的效益进行对比分析。每种机制所对应的车辆总行驶时间均为随机模拟100次的平均值。

当σ=11，m=20，f∈{1,2,…,8}，各机制对应的车辆总行驶时间见表2，表3为不同路段行驶时间增加量下各机制对应的总行驶时间，表4为不同影响路段数下各机制对应的总行驶时间。

图7 最终车辆配送路线图

表2不同干扰频率下各机制对应的总行驶时间

Tab.2Totaltraveltimesofthreeadjustmentmechanismsontheconditionofdifferentdisturbutionfrequenciesmin

f12345678机制1866.67869.90872.42874.87876.69880.05883.20887.14机制2866.35868.36870.71873.16875.35878.05879.62882.90机制3866.02868.41870.22872.15873.69876.51878.53880.99差值1(1-3)0.651.492.22.723.003.544.666.14差值2(2-3)0.33-0.050.491.011.661.541.091.91

表3 不同路段行驶时间增加量下各机制对应的总行驶时间

从表2～4可得出结论如下。

1) 对于任一干扰频率f、路段行驶时间增加量σ以及影响路段数m，更新机制(机制2和机制3)的总行驶时间都小于不更新机制的总行驶时间，而且其差值随偶发拥堵因素影响的加剧而增大。这表明更新机制比不更新机制可获得更好的效益；且随着偶发拥堵因素对路网影响的加剧，效益更显著。这源于更新机制能调整车辆配送路线避开受偶发拥堵因素影响的路段；且随着偶发拥堵因素对路网影响的加剧，配送路线避开偶发拥堵因素所影响的路段次数或避开1条受影响路段效益随之增加。

表4 不同影响路段数下各机制对应的总行驶时间

2) 除σ=5,7；m=20，任一干扰频率f、路段行驶时间增加量σ以及影响路段数m，可额外获知偶发拥堵持续时间信息的更新机制比只能根据新获知路段行驶时间信息调整车辆配送路线有更好的效益。这是由于获知偶发拥堵持续时间信息，可避免为躲避不会对车辆行驶时间产生影响的偶发拥堵而产生绕行，从而进一步减少车辆总行驶时间。且其效益随着偶发拥堵因素对路网影响的加剧而更显著。这是因为随着偶发拥堵因素对路网影响的加剧，获知偶发拥堵持续时间信息避免不必要绕行的次数增加。

4 结束语

笔者对可获知偶发拥堵持续时间的动态取送一体化车辆路径问题进行了研究。以改进的Dijkstra算法分别根据常发拥堵信息和不断获知的偶发拥堵信息获得客户点间最短行驶时间，依据常发拥堵信息以遗传算法安排车辆初始配送路径，依据偶发拥堵信息结合2-opt法和insertion法更新车辆配送路径，通过车载导航系统实时指导配送车辆去往下一个客户点的行驶路线。经数值试验表明，笔者采用方法可根据偶发拥堵持续时间信息调整车辆配送路线，避开受偶发拥堵因素影响路段，缩短车辆行驶时间；且其比不更新配送路线以及只根据新获知的路段行驶时间信息更新配送路线有更好的效益，且该效益随着偶发拥堵因素对路网影响的加剧而更显著。未来可进一步研究获知的偶发拥堵信息不准确情形下的动态车辆路径问题。

参考文献

References

[1] CRAINIC T G, LAPORTE G. Planning models for freight transportation[J]. European Journal of Operational Research,1997,97(3):409-438.

[2] 饶卫振,金 淳,刘 锋,等.一类动态车辆路径问题模型和两阶段算法[J].交通运输系统工程与信息,2015,15(1):159-166.

RAO Weizhen, JIN Chun, LIU Feng, et al. Model and two-stage algorithm on dynamic vehicle routing problem[J].Journal of Transportation Systems Engineering and Information Technology,2015,15(1):159-166. (in Chinese)

[3] 李妍峰,高自友,李 军.基于实时交通信息的城市动态网络车辆路径优化问题[J].系统工程理论与实践,2013,33(7):1813-1819.

LI Yanfeng, GAO Ziyou, LI Jun. Vehicle routing problem in dynamic urban network with real-time traffic information[J]. Systems Engineering-Theory & Practice,2013,33(7):1813-1819. (in Chinese)

[4] 李妍峰,高自友,李 军.动态网络车辆路径派送问题研究[J].管理科学学报,2014(8):1-9.

LI Yanfeng, GAO Ziyou, LI Jun. Dynamic vehicle routing and dispatching problem[J]. Journal of Management Sciences in China,2014(8):1-9. (in Chinese)

[5] PILLAC V, GENDREAU M, GUéRET C, et al. A review of dynamic vehicle routing problems[J]. European Journal of Operational Research,2013,225(1):1-11.

[6] MALANDARAKI C, DASKIN M. Time dependent vehicle outing problems: Formulations, properties and heuristic algorithms[J]. Transportation Science,1992,25(3):185-200.

[7] ICHOUA S, GENDREAU M, POTVIN J. Vehicle dispatching with time-dependent travel times[J]. European Journal of Operational Research,2003,144(2):379-396.

[8] GHIANI G, GUERRIERO E. A note on the ichoua, gendreau, and potvin (2003) travel time model[J]. Transportation Science,2014,48(3):458-462.

[9] POTVIN J, XU Y, BENYAHIA I. Vehicle routing and scheduling with dynamic travel times[J]. Computers & Operations Research,2006,33(4):1129-1137.

[10] LORINI S, POTVIN J, ZUFFEREY N. Online vehicle routing and scheduling with dynamic travel times[J]. Computers & Operations Research,2011,38(7):1086-1090.

[11] TANIGUCHI E, SHIMAMOTO H. Intelligent transportation system based dynamic vehicle routing and scheduling with variable travel times[J]. Transportation Research Part C: Emerging Technologies,2004,12(3-4):235-250.

[12] OKHRIN I, RICHTER K. Vehicle routing problem with real-time travel times[J]. Int. J. Vehicle Information and Communication Systems,2009(2):59-77.

[13] 姬杨蓓蓓.交通事件持续时间预测方法研究[D].上海：同济大学,2008.

JIYANG Beibei.Research on prediction method of traffic incident duration[D].Shanghai：Tongji University,2008. (in Chinese)

[14] KOK A L, HANS E W, SCHUTTEN J M J. Vehicle routing under time-dependent travel times: The impact of congestion avoidance[J]. Computers & Operations Research,2012,39(5):910-918.

[15] JUNG S, HAGHANI A. Genetic algorithm for the time-dependent vehicle routing problem[J]. Transportation Research Record: Journal of the Transportation Research Board,2001(1771):164-171.

[16] OMBUKI B M, ROSS B J, HANSHAR F T. Multi-objective genetic algorithms for vehicle routing problem with time windows[J]. Applied Intelligence,2006,24(1):17-30.

[17] BEAN J C. Genetic algorithms and random keys for sequencing and optimization[J]. ORSA Journal on Computing,1994,6(2):154-160.

[18] 靳志宏,计明军.物流实用优化技术[M].北京：中国物资出版社,2008.

JIN Zhihong, JI Mingjun. Practical optimization technologies for logistics[M]. Beijing：China Fortune Press,2008. (in Chinese)

[19] 张 燕,周支立,翟 斌.集货送货一体化的物流配送车辆路线问题的标号算法[J].运筹与管理,2007(3):12-18.

ZHANG Yan, ZHOU Zhili, ZHAI Bin. Multi-attribute label matching algorithm for vehicle routing problems with time windows and backhauls[J].Operations Research and Management Science,2007(3):12-18. (in Chinese)

[20] GENDREAU M, GHIANI G, GUERRIERO E. Time-dependent routing problems: a review[J]. Computers & Operations Research,2015(64):189-197.

[21] FLEISCHMANN B, GIETZ M, GNUTZMANN S. Time-varying travel times in vehicle routing[J]. Transportation Science,2004,38(2):160-173.