波形钢板的弹性稳定分析

1 概 述

钢板剪力墙是20世纪70年代兴起的一种高效的抗侧力结构体系,主要由边缘框架柱,框架梁和内嵌钢板组合而成,常用于高地震烈度地区的多高层钢结构建筑。钢板剪力墙在剪力作用下通过斜向拉力场来抵抗水平侧向荷载,虽然钢板剪力墙有着侧向承载力高,延性和耗能能力高等一系列优点,但其在施工和使用过程中会出现一些问题,施工过程中钢板墙往往需要等框架与楼板就位以后才能安装,否则传递到钢板墙的重力荷载会引起薄钢板的弹性面外屈曲,对工期有一定的影响,在强风或小震作用下,钢板墙会发生弹性面外屈曲并伴有噪声,影响用户的舒适性；钢板墙弹性屈曲后结构的抗侧刚度明显下降[1]。以上不足在一定程度上制约了钢板墙在中国的高层建筑中的应用与发展。

国内学者也有将波形钢板引入到钢板剪力墙结构中,有竖向波形钢板和横向波形钢板两类,其中竖向波形钢板可以承担竖向荷载,横向波形钢板释放竖向荷载[2]。对于波形钢板的弹性屈曲分析,多数是基于数值方法求解剪切弹性屈曲[3],很少有关抗压弹性屈曲,李靓娇在其论文中有提到受压弹性屈曲理论公式,是在平钢板弹性屈曲理论公式基础上修改相关参数,并采用有限元数据拟合得到的相关公式[4]。本文对波形钢板受压弹性屈曲从平衡方程的角度进行解析解推导,并采用有限元进行论证。有关剪切弹性屈曲,相关理论解答在国外文献[5]中有所提到,根据有关国内文献指出该理论解小于数值解,本文从有限元角度论述该理论解与实际情况相差较远的原因。

2 波形钢板的构造

波形钢板应用于钢板剪力墙结构中,是两边连接端柱,上下连接钢梁的构造组成,形成便于稳定受力的剪力墙,有别于传统钢板剪力墙体系,既可以承受水平力,也可以承受竖向力,在局部稳定满足的情况下,可以按压弯构件进行整体强度、稳定计算。其中带边框的波形钢板组合墙截面示意图见图1。

图1 带边框的波形钢板组合墙截面

3 波形钢板弹性稳定分析

3.1 单向均匀受压简支波形钢板弹性稳定分析

根据铁木辛柯板壳理论[6],异形板的稳定平衡微分方程为

(1)

式中：ω为板的变形挠曲面方程；

px、py、pxy为面内各项薄膜内力。

设置坐标系,令高度方向为x向,宽度方向为y向。顶面施加均布荷载p,因此中面力py=0、px=-p、pxy=0,代入式(1)得到,

(2)

式中：Dx为波形钢板x向单位宽度的抗弯刚度；

Dy为波形钢板y向单位宽度的抗弯刚度；

H为与波形钢板抗扭刚度有关的一个参数。

根据铁木辛柯板壳理论,此时

式中:Ix为波形钢板x向单位宽度的惯性矩。

根据板的边界条件,确定板的挠曲面方程为[7]

(3)

式中:m、n、a、b分别代表x向半波数,y向半波数,板高度,板宽度。

代入上述微分方程(2)得到,

(4)

屈曲条件为括弧内的式子为零,则

(5)

(6)

因板高度受限在层高范围内,因此一阶失稳模态时一般n=1,m=1,得到

(7)

弹性临界应力为

(8)

3.2 均匀受剪简支波形钢板弹性稳定分析

异形板的屈曲模式有三种：局部屈曲,整体屈曲以及相关屈曲。相关研究表明,波形的几何形状(波宽,波高)和板件尺寸影响着屈曲模式,波形稀疏时局部屈曲为主,波形密集时,整体屈曲为主。四边简滞异形板弹性剪切整体屈曲的理论公式为[5]

(9)

式中:hw相当于波形钢板的高度a。

本文采用有限元方法对波形钢板的弹性剪切性能进行分析。根据工程中常用的波形钢板剪力墙尺寸,确定相关参数见表1。

表1 波形钢板墙尺寸(不含端柱与钢梁)

备注:楼层更高情况,设置横隔板等加劲肋；宽度范围涵盖了短肢剪力墙与剪力墙两类。

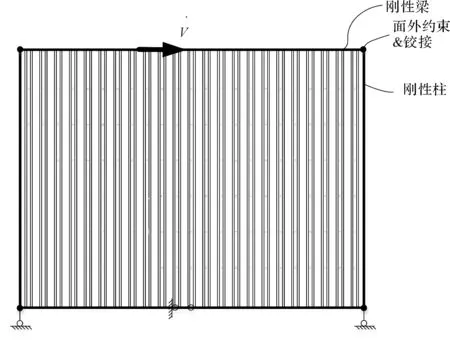
图2 剪切屈曲模型示意图

为了模拟波形钢板的受剪工况,将钢梁与端柱按刚性构件考虑,剪切屈曲分析模型示意图见图2。

经分析得到各编号的墙体剪切屈曲模态示意图见图3。

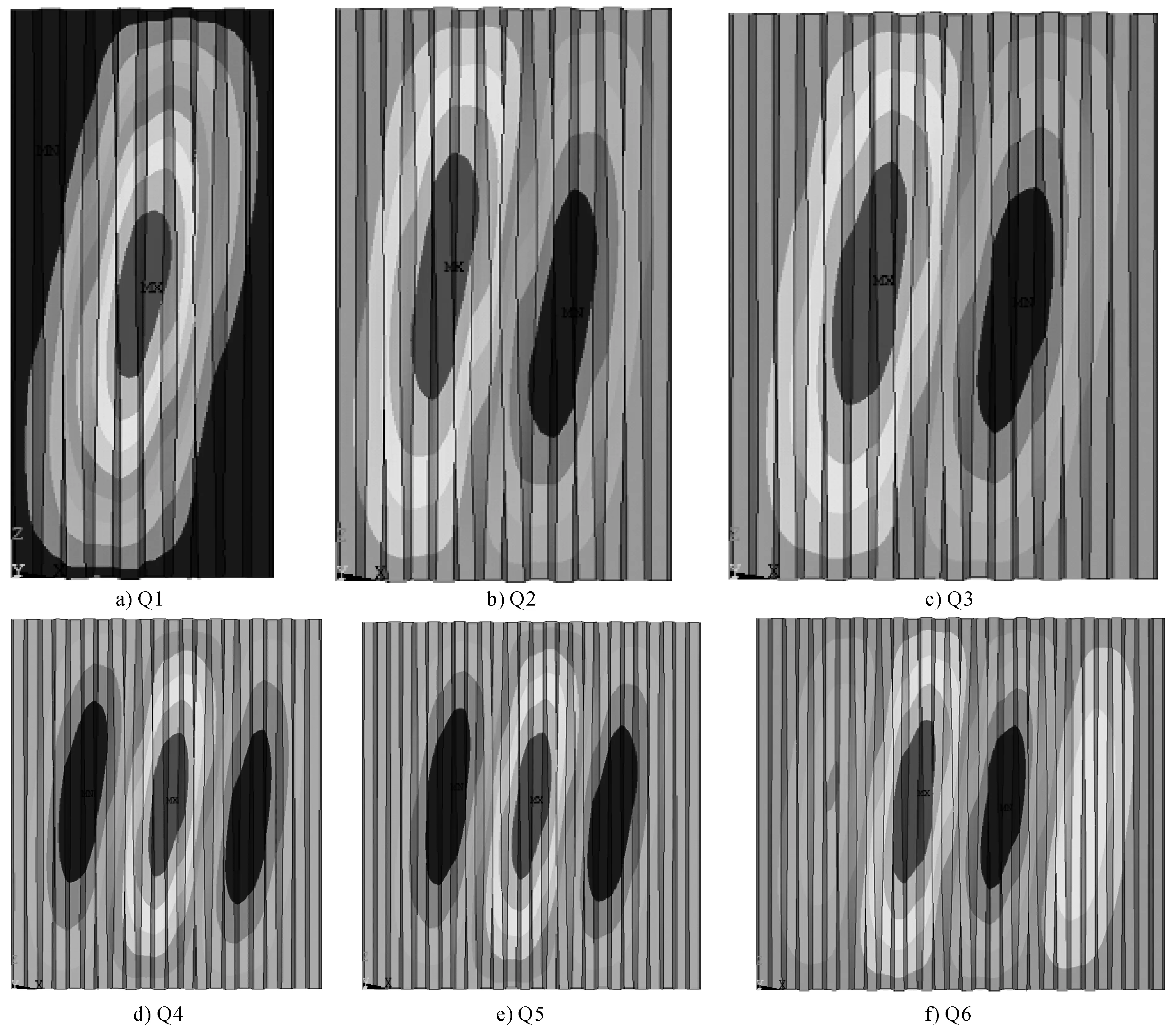
图3 不同墙体宽度一阶弹性受剪屈曲模态

从图3可知,板件受剪屈曲随宽度的增加,呈现节间凹凸现象,且在同一板件中每个节间宽度是不同的,只有当宽度远远大于高度时,节间宽度是定值,这与平板剪切屈曲模态是一致的[8]。一般情况下,在平板剪切屈曲时,当a大于b,或a与b较相近时,在宽度方向只可能是一个半波的屈曲模态,而波形钢板的剪切屈曲模态从图3可知,即使宽度b比高度a小时,在宽度方向也出现了多个半波的情况,原因是波形钢板在两个方向的抗弯刚度悬殊,即a方向的抗弯刚度较b方向的抗弯刚度大很多,若等效为平钢板情况,需要a方向高度变矮成为a1以此等效抗弯刚度,因a1远小于b,因此宽度b方向出现了多个半波。临界剪应力随宽度的变化见图4。

图4 临界剪应力随板宽度的变化

根据式(9)可知,剪切应力与宽度b没有关系,从图4可知,剪应力与宽度有反比的关系,式(9)更适用于宽度远大于高度的情况,比如波形腹板的情况,对于剪力墙结构高宽比较大的情况,式(9)是不适用的,误差较大。

4 结 语

本文论述了波形钢板较平钢板在剪力墙结构应用上的差别,波形钢板在受压工况下有更好的优势。波形钢板属于异形板,根据铁木辛柯经典理论描述了波形钢板的稳定平衡微分方程,从理论上解析了波形钢板受压弹性屈曲性能,并采用有限元加以验证,两者吻合较好；对于工程常用的剪力墙高宽比尺寸,采用有限元数值模拟得到其弹性剪切应力,对其屈曲模态与平钢板屈曲模态的差异进行说明,并说明现有整体剪切屈曲公式不适用于常规高宽比的波形钢板剪力墙。

参 考 文 献

[1] 孙军浩.波纹钢板剪力墙的抗侧及抗震性能研究[D].天津:天津大学,2015．

[2] 朱文博.波纹钢板组合剪力墙力学性能研究[D].郑州：郑州大学,2017．

[3] 赵秋红, 李楠, 孙军浩. 波纹钢板剪力墙结构的抗侧性能分析[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(增刊1):152-160．

[4] 李靓姣. 波浪形钢板墙的受力性能及设计方法研究[D]. 北京：清华大学, 2012．

[5] Galambos T V. Guide to Stability Design Criteria for Metal Structures[M].New York:John Wiley and Sons,1988．

[6] 铁木辛柯.板壳理论[M].北京：科学出版社,1977．

[7] 陈骥.钢结构稳定理论与设计[M].5版.北京：科技出版社,2011．

[8] 陈绍蕃,陈传铮,顾强.现代钢结构设计师手册[M].北京:中国电力出版社,2006.