基于标签分布学习森林的电价概率预测

王 翔

(华北电力大学，北京 102206)

0 引言

电价作为电力系统实行市场化运行的核心内容，很大程度上决定了市场参与者的成本与利润。发电商需要准确预测电价以便做出竞标策略，来规避风险，追求最大收益；供电企业也需要根据准确的电价预测信息来规划其在现货市场和长期双边合同中购电量的最优购买分配方案；投资者也同样需要参考准确的电价预测信息做出正确的投资决策。因此，准确的电价预测已成为电力市场各参与者共同关注的焦点[1]。

然而，由于影响因素众多[2]，如系统负荷需求，燃料价格，国民经济发展水平，市场参与者对电价的预期等，电价常表现出较强的波动性与随机性，使得准确预测电价的成为电力市场众多的研究难点之一。

近年来，众多学者专家就短期电价预测进行了大量的研究，尝试了多种预测模型和方法。现有的电价预测方法大致可分为两类，即市场模拟法和基于历史数据的预测方法。

市场模拟法，如随机生产模拟[3-4]，是通过模拟电力市场的竞争运营，来预测市场价格，但是，由于模拟法需要大量的系统、数据结构，计算量大，从而限制了其在较大电力系统中的应用，并且在进行模拟实体或环境条件实验时，难以完全表现真实情境，容易出现对知识的片面理解，从而导致实验准确度不高；基于历史数据的预测方法，如神经网络模型[5-8]，支持向量机[9]，时间序列法[10-13]和组合预测法[14-17]等，其特点是所需要的数据量相对较少，主要利用电价的长期历史数据来预测市场价格。在基于历史数据的概率学预测研究方面，文献[18]基于非线性分位数回归理论，利用神经网络计算概率分布，文献[19]把支持向量回归与核密度估计结合来计算概率密度函数。以上研究均未考虑时间因素的影响。文献[20]考虑到电价的时序性特点，建立自回归条件异方差模型对电价进行预测，但是对计算量较大，电价波动异常，电价序列相邻时段相关性较弱的电力市场来说，适用性较差。

本文提出了一种基于标签分布学习森林(Label Distribution Learning Forests，LDLFs)的电价概率预测模型，主要考虑负荷对实时电价的影响，与上述主要对短期电价进行点预测的预测方法相比，基于LDLFs的电价预测模型能得到实时电价的概率密度函数，它比点预测更能体现出电价的不确定性，可为发/售电提供更多的有用信息，这对电价波动异常的电力市场同样适用。该模型由一个线性模型和可微决策森林组成，以电价、时间与负荷数据做输入特征，经线性变换得到新的抽象特征，然后随机指派到分裂结点，在分裂结点的概率分裂函数下划分到左右子树，最终由叶子结点输出电价的概率密度函数。在新加坡电力市场的电价数据集上的实验结果显示，本文所提方法不仅体现了电价的不确定性，而且与其他概率预测方法相比具有较高的预测精度。

1 基本原理

1.1 标签分布学习概述

标签分布学习(LabelDistributionLearning,LDL)是一个处理分类问题中标签模糊性问题的学习框架。LDL不是为一个实例分配一个或多个标签，而是学习对于给定实例的描述中标签间的相对重要性，例如一组标签集合的分布，在人脸年龄估计、影评打分预测等任务中有了初步的应用。标签分布学习可以形式化为如下问题：

令X=Rm表示输入空间[21]，Y={y1,y2,…,yc}表示完成的标签集，其中C是可能标签值的个数。那么，标签分布学习问题可以看作，对于每一个样本x∈X，都有一个标签分布这里，表示样本x属于第c个标签yc的概率，因此满足约束条件LDL的目标是学习输入样本x和它对应的标签分布d之间的映射函数g:x→d。

标签分布学习的方法包括最大熵模型及表示、Boosting和SVR扩展等方法，但是它们要么由于模型的指数部分限制了分布形式的泛化，要么在表示学习上的局限性导致无法端到端的学习抽象特征。Shen等人[22]提出利用标签分布学习森林解决标签分布学习问题，得到了很好的效果。

1.2 基于标签分布学习森林的电价概率预测模型

受到标签分布学习森林的启发，本文提出基于标签分布学习森林的电价概率预测模型，将标签分布学习中的离散标签学习问题扩展到电价概率预测领域中的连续概率密度函数问题。具体概率预测模型如图1所示。

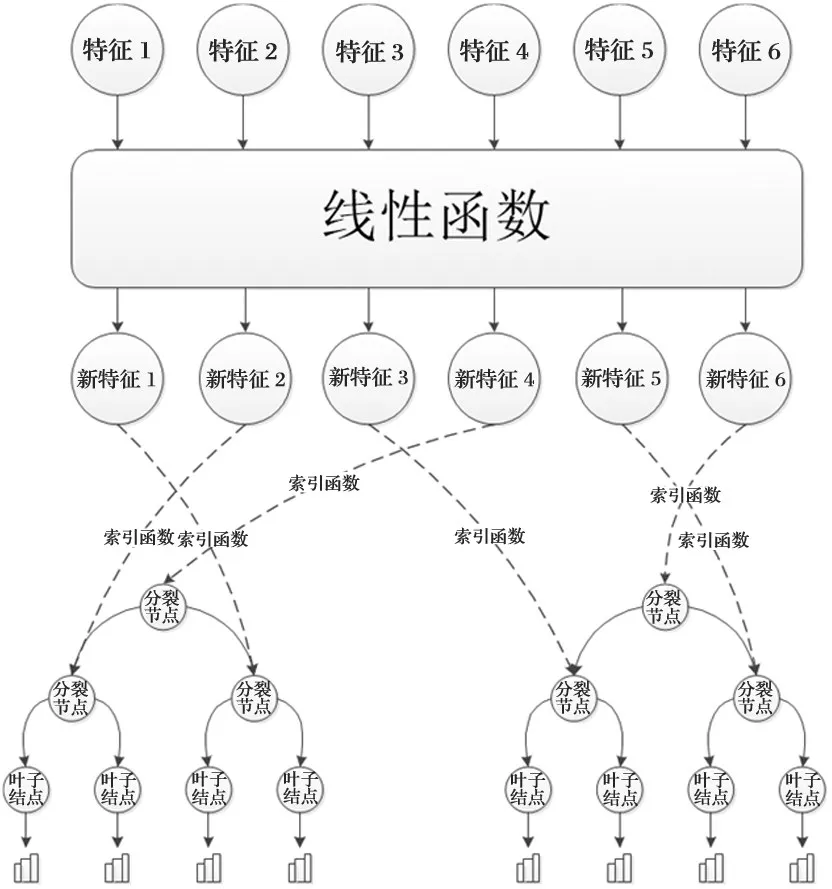
图1 标签分布学习森林电价概率预测模型流程图

本模型由一个线性函数f和多个可微决策树形成的可微决策森林组成。

一颗决策树包括一组分裂节点N和一组叶子节点L。在每个分裂节点n∈N定义了一个分裂函数该函数以为参数，决定一个样本应该被放入左子树还是右子树，每个叶子节点具有一个在标签集Y上的分布为了构建一个可微决策树[23]，使用概率分裂函数其中σ(·)是一个sigmoid函数，φ(·)是一个索引函数，将函数的第个输出与分裂节点n联系上，f:x→RM是一个依赖于样本x和参数Θ的实值特征学习函数。

分裂节点和函数f的输出单元之间的联系由φ(·)表示，在树的学习之前是随机产生的，之后，样本x落入叶子节点l的概率：

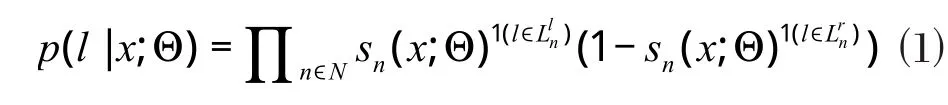
其中，1(·)是指示函数，分别代表节点n的左子树和右子树所拥有的叶子节点的集合，最终得到树τ的输出，即映射函数g定义为：

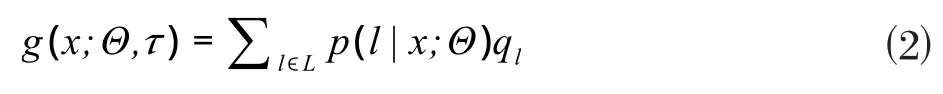
和其他模型相比，标签分布学习森林的优点在于整个模型从原始特征输入到电价概率输出是一个端到端的学习过程，在整个模型训练过程中无需再对数据进行处理。模型一体化学习的能力极大地减轻了工作量。

2 案例分析

2.1 数据处理与精度度量

本文以2017年新加坡电力数据集为实证研究对象。由于电价是一个时间序列，因此，本文选取前十个点的电价、负荷及时刻点作为特征来预测第十一个点的电价，采取十折交叉验证进行试验。

在进行预测之前，先对数据进行归一化处理以消除量纲影响：

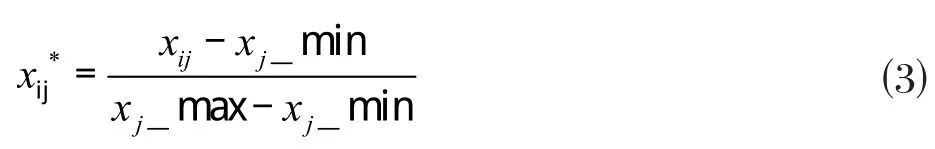
式中：为第j个指标第i个样本归一化值；xij为该样本指标原始值；xj_min为第j个指标所有样本中的最小值；xj_max为第j个指标所有样本中的最大值。

由于模型得到的是电价的概率密度曲线，用之前点预测的损失函数来衡量预测误差的效果并不理想，这里采用相对熵(Kullback-Leibler divergence，KLD)方法来度量。

相对熵的一般表达式为：

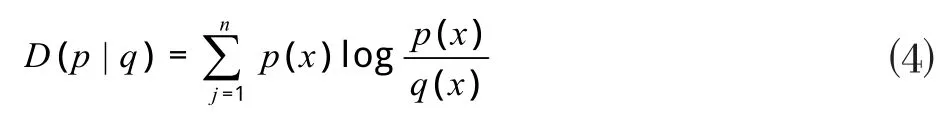
式中：p(x)为电价的真实概率密度，q(x)为预测电价概率密度，n为样本可能标签值的个数。

2.2 预测结果

实验采用能源市场资源股份有限公司(Energy Market Company PteLtd)在新加坡电力市场的经营数据，选取2017年3月1日到5月30日批发电价及需求负荷数据作为测试算例，每隔半个小时一个数据点，共4416个数据点。考虑到电价是个时序特征，本文将相应时刻点与星期得到独热向量，也作为特征输入，采用十折交叉验证进行了大量的预测验证工作，下面给出预测结果：

图2是3月1日到5月30日间随机抽取某一天的短期电价预测结果与真实结果概率密度曲线的对比，可以看出，在经过500次迭代后，预测曲线已经非常接近真实曲线，此时KLD=0.109014。从图3上可以明显看出，预测电价峰值总出现在真实电价周围，且相距很近，预测结果良好。

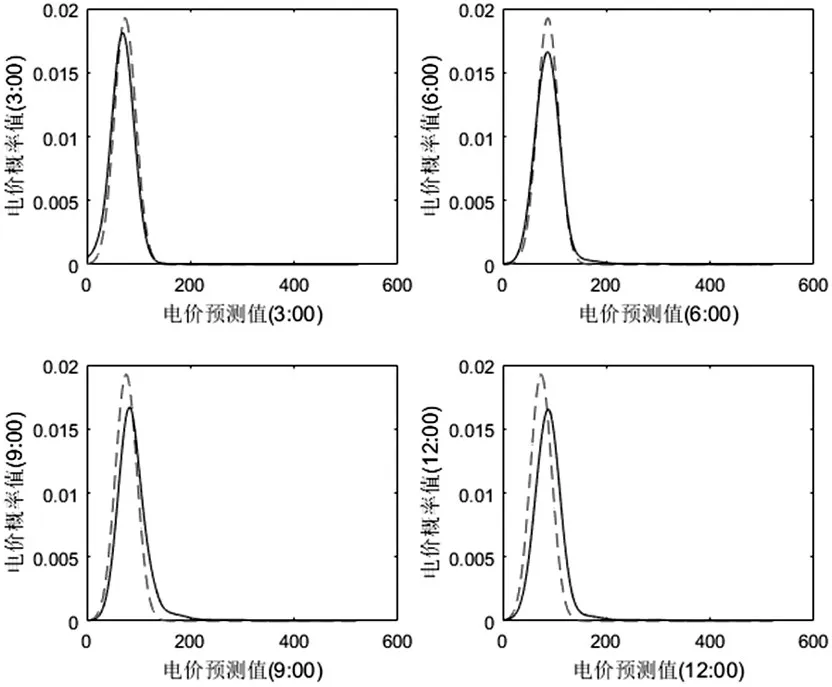
图2 真实电价与预测电价概率密度曲线对比图

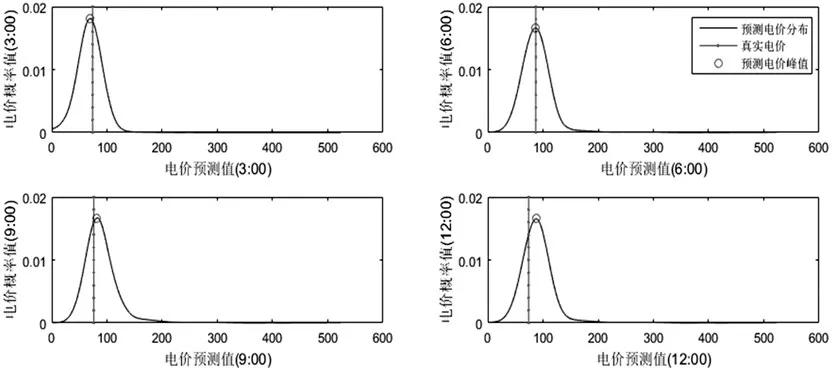
图3 真实电价与预测电价峰值对比图

为了更好地说明本文方法的预测效果，采用相同数据，用另外三种模型对2017年5月31日的24个时间段进行电价预测。

第一种为支持向量分位回归模型(support vector quantile regression，SVQR)，以0.01为步长选取100个分位点分别进行训练，将训练得到的模型预测结果经统计得到电价概率密度曲线；第二种同样选取100个分位点，但在综合预测结果时采取核密度估计(Kernel density estimation，KDE)的方法；第三种采取本文提出方法，但是不包含时刻点。4种模型的电价预测结果如表1所示。

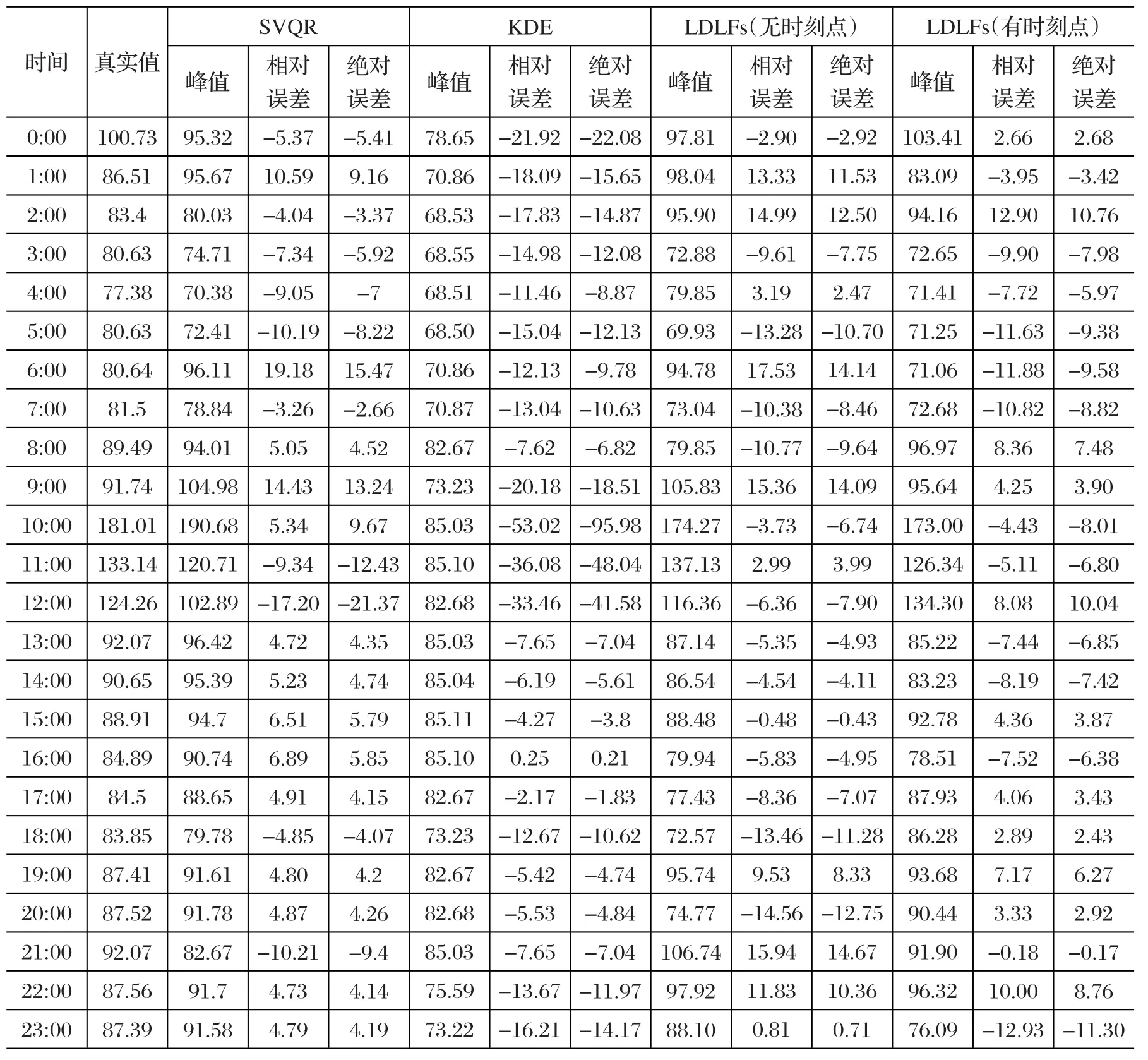
表1 各方法日前电价数据对比

与其他三种方法相比，本文提出的方法对于电价波动较大的电力市场来说仍具有比较好的预测精度。同时，考虑到电价的时序性特点，本文将时间作为特征输入，事实证明，考虑时间序列的LDLFs模型能得到更好的实时电价预测结果。

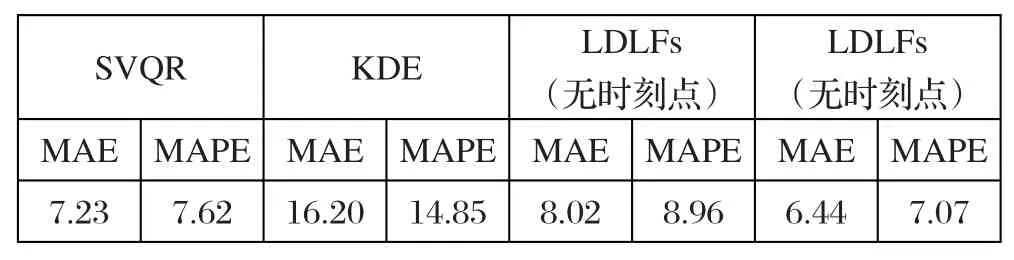
表2 各方法日平均百分比误差比较

3 结论

针对电力市场中电价时间序列的非平稳随机性特点，本文提出了基于标签分布学习森林的电价概率预测模型。通过对新加坡电力市场历史数据的验证，得出以下结论：

⑴ 本文方法充分考虑到了电价的时序性，将时刻点也纳入考虑范围；

⑵ 本文模型所得结果体现了电价非平稳随机性的特点，同时具有一定精度；

⑶ 本文所提方法在进行算例测试时，较对比模型取得了更好的预测效果，对一些电价波动异常的时刻点也同样适用，这说明线性函数与可微随机森林的组合算法可以较好地处理电价概率预测问题。

参考文献(References):

[1]刘丽燕,邹小燕.GARCH族模型在电力市场电价预测中的比较研究[J].电力系统保护与控制,2016.44(4):57-63

[2]刘达,牛晓东,杨光.电力市场中的电价影响因素[J].陕西电力,2009.1:9-12

[3] H.Y Yamin.Adaptive short-term electricity price forecasting using artificial neural networks in the restructured power markets[J].International Journal of Electrical Power&Energy Systems,2004.26(8):571-581

[4]Florian Ziel,Rick Steinert.Electricity Price Forecast using Sale and Purchase Curves:The X-Model[J].Energy Economics,2016.59(3):435-454

[5]王萌,景志滨,孙兵,等.基于BP神经网络的短期市场出清电价预测[J].中国电力教育,2011.30:100-102

[6]翁陈宇.基于神经网络的短期电价预测[D].西南交通大学硕士学位论文,2007.

[7]Zabir Haider Khan,Tasnim Sharmin Alin,Akter Hussain.Price Prediction of Share Market Using Artificial Neural Network 'ANN'[J]. InternationalJournal of Computer Application,2011.22(2):42-47

[8]吴兴华,周晖.基于减法聚类及自适应模糊神经网络的短期电价预测[J].电网技术,2007.19:69-73

[9]Yao Gao Chen,Guangwen Ma,Electricity Price Forecasting Based on Support Vector Machine Trained by Genetic Algorithm[C],2009:292-295

[10]赵军.基于区域和时间序列及电价政策的电网负荷建模研究[J].华东电力,2017.9:104-105

[11]宁艺飞,陈星莺,颜庆国等.分时电价下大用户概率响应建模研究[J].电力需求侧管理,2017.19(1):22-28

[12]邓佳佳,黄元生,宋高峰.基于非参数GARCH的时间序列模型在日前电价预测中的应用[J].电网技术,2012.36(4):190-196

[13]夏君常.电力市场短期电价预测的时间序列模型研究[D].重庆大学硕士学位论文,2011.

[14]Akash Saxena,Sinrath Lal Surana,Deepak Saini.Hybrid Approach of Addictive and Multiplicative Decomposition Method for Electricity Price Forecasting[J],2017.

[15]Deepak Sain,Akash Saxena,R.C Bansal.Electricity price forecasting by linear regression and SVM[C],2017.

[16]Abbas Rahimi Gollou,Noradin Ghadimi,Abbas Rahimi Gollou等.A new feature selection and hybrid forecast engine for day-ahead price forecasting of electricity market[J].JournalofIntelligent& Fuzzy Systems,2017:1-15

[17]牛丽肖,王正方,臧传治等.一种基于小波变换和ARIMA的短期电价混合预测模型[J].计算机应用研究,2014.31(3):688-691

[18]何耀耀,许启发,杨善林等.基于RBF神经网络分位数回归的电力负荷概率密度预测方法[J].中国电机工程学报,2013.33(1):93-98

[19]何耀耀,闻才喜,许启发,撖奥洋.考虑温度因素的中期电力负荷概率密度预测方法[J].电网技术,2015.39(1):176-181

[20]刘丽燕.基于非参数GARCH模型的电力市场日前电价预测研究[D].重庆师范大学硕士学位论文,2016.

[21]X Geng.Label Distribution Learning.IEEE Trans.Knowl.Data Eng.,2016.28(7):1734-1748

[22]Shen W,Zhao K,Guo Y等.Label Distribution Learning Forests[C].In Advances in Neural Information Processing Systems,2017:834-843

[23]P.Kontschieder,M.Fiterau,A.Criminisi等.Deep neural decision forests[J].ICCV,2015:1467-1475