特高压输电线路树障隐患预判及仿真分析
祝 贺,于卓鑫,严俊韬
(东北电力大学建筑工程学院,吉林吉林132012)
特高压直流输电线路可提升资源开发和利用效率,具有卓越的经济收益和社会效益[1~4].但输电线路输电距离较长,不得不大量跨越灌木丛林.由于树木生长速度极快,树高不断逼近架空导线,当树木生长高度至架空导线安全范围内,易使导线被击穿引发跳闸停电事故.国内外已发生多起输电线路树障隐患事故,据海南电网近3年统计树障隐患致使线路跳闸共35次,广东电网由树障隐患致线路跳闸事故占总跳闸事故46%[5].2006年~2007年间,马来西亚东部因树木生长过高,导线与树木枝杈绞缠发生大爆炸致使该区域大面积停电[6].
目前,针对输电线路树木隐患的研究大多集中于在线监测技术,在各个杆塔上安装摄像装置,通过采集回来的监测图像对是否存在树木隐患进行预判[7~10].但由于图像不能精准的显示距离摄像装置较远的弧垂点和树冠,判断净空距离存在误差.
为降低树障隐患在线监测技术存在的净空距离监测误差,避免由树木生长过高而导致跳闸停电事故的发生.本文以云南-广州±800kV特高压输电线路为研究对象,根据架空导线与树的空间位置,将树障隐患分为线下树障和临线树障.首先,针对线下树障隐患,通过建立包含风速、温度在内的导线应力动态数学模型和树高预测数学模型,作为树障的动态边界条件.从而得到线下树障净空距离预判模型.其次,针对临线树障隐患,考虑架空导线在风荷载、自重荷载作用下,建立导线结构动力学方程,完成导线运动轨迹的描述.通过对导线与树冠之间的空间畸变电场,与线路间隙击穿场强进行比较,对临线树障进行预判,从而提高架空线路供电稳定性.
1 线下树障隐患预判
由于导线下方树木生长过高,导线与树冠之间空间垂直距离过近,导致线路跳闸停运.线下树障是树闪事故多发的重要原因之一,对线路造成极大威胁.因此,构建针对线下树障隐患垂直净空距离预判模型尤为重要.
1.1 建立导线应力动态数学模型
导线温度是一个随时间动态变化的过程,导线温度的升降会引起架空线的热胀冷缩,使导线线长、弧垂、应力发生相应变化.当温度升高时,导线应力弧垂变大[11].

式中:T为导线温度,℃;m为单位长度导线的质量,kg/m;Cp为导线综合热容系数J/kg·℃.
导线温度的变化影响其应力弧垂的大小,大风同样会造成架空线比载增加,使应力变大.利用架空线的状态方程,建立包含风速、温度的应力动态数学模型.

式中:σm、σn分别为m、n状态下架空线弧垂点处的应力,MPa;rm、rn分别为两种状态下架空的比载,MPa/m;tn、tm分别为导线的温度,℃;l为该档的档距,m;α、E分别为架空线的温度膨胀系数和弹性系数.
对公式(2)整理可得:

令:
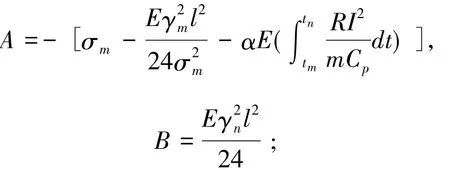
则:

求解公式(4)得到包含风速、温度的应力动态数学模型.
1.2 计算架空导线任一点处弧垂
根据应力动态数学模型,可推导出弧垂和应力之间的非线性数学关系.由于应力随导线温度和风速变化,故通过导线应力动态数学模型和弧垂公式(5),则可求出输电线路任一点处的导线弧垂.

式中:γ为当地气象条件下比,MPa/m;l为档距,m;σn为包含风速和温度随时间变化的应力,MPa;β为不等高导线代表高差角,℃.
1.3 建立树高生长预测模型
输电线路线下树木隐患主要由树木生长过高所致,因此预测树木生长高度可有效地对线 -树净空距离进行预判,减少树障事故的发生.本文采用理查德生长方程对树木生长高度进行预测.
理查德生长方程是根据不同树种的各生长调查因子为基础,对树高生长量随时间变化规律进行描述[12].此方程适用性广泛、预测拟合准确性高和合理性强,因此,Richards方程在近代林业树木生长高度预测中被广泛应用[13~14].
理查德生长方程为

生长方程中参数t为树木生长年龄,y为树高生长量,参数a、k、c为生长调查因子,其中k是模拟树木生长高度其生长规律的修订参数,修订值在0-1之间.由式(6)可知,Richards生长方程是非线性回归数学模型.生长方程中各参数的求定应用程序软件Microsoft Excel 2010.根据不同的立地条件,在实际调查中得到多组树高观测数据列于Excel中,如表1所示.在Excel软件操作页面选中树木生长年龄和树木高度观测数据区域,绘制树龄-树高观测值散点图并添加趋势线,并对三组树高观测值进行拟合得到回归方程.

表1 树龄与树高观测值
根据观测数值绘制散点图,并添加趋势线可清楚地得到桉树生长趋势,如图1所示.
在Excel中绘制桉树树高生长曲线时,软件对桉树树高和树龄自动进行拟合,并得到回归方程:y=-0.102 6x2+4.312x - 24.141,其中 R2=0.990 3 为回归方程的拟合度,拟合度越接近1,则说明拟合优度高,反之则越差.取三个树龄代入回归方程中求得相应的理论树高值,树龄分别取10年、15年、20年,所求的相应树高为H1=8.719、H2=17.454、H3=21.059.
根据H1、H2、H3求其观测比如公式(7)所示:

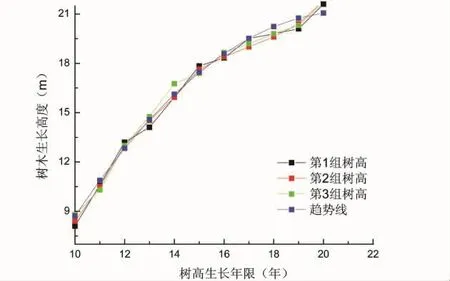
图1 桉树树高生长曲线图
为确定各参数值,将H1、H2、H3代入公式(6)与公式(7)联立可得:

令 e-10k=x,λ =0.787 则可得:

确定观测比后,求定生长方程中各参数值.对公式(9)中的x进行规划求解,从而可求定各参数结果如表2所示.
综上所述,树高预测模型为


表2 树高模型各参数求定
1.4 建立线下树障净空距离数学模型
根据应力动态数学模型、弧垂和应力之间的非线性数学关系、Richard树木生长高度预测方程,可构建出线下树障导线距树木的最小净空距离数学模型,如图2所示.
导线距树冠最小净空距离数学模型:

式中:H为极导线距树冠最小垂直距离,m;h为杆塔高度,m;f为导线任意点弧垂,m;y为乔木树高生长模型拟合结果,m;Δh为施工裕度,m.

图2 线下树障净空距离示意图
根据《±800 kV直流架空输电线路设计规范》(GB 50790)规定导线距树木最小垂直距离小于13.5 m.在对线下树障隐患进行预判时,运用线下树障净空距离数学模型,如图2所示.当H<13.5 m时,符合规定不会发生树闪故障.当H≥13.5时,存在树闪故障隐患,巡线工作人员应当及时对故障树木进行修剪,排除故障隐患.
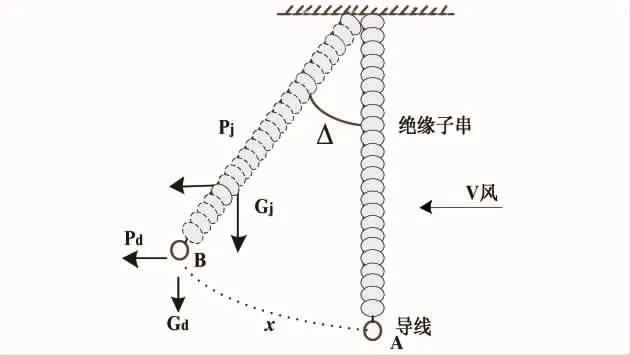
图3 导线风偏角示意图
2 临线树障隐患预判
在建立导线动态应力状态方程和树木生长高度预测数学模型,以及求解线下树障判距的基础上,考虑架空导线在风、自重作用下,建立导线结构动力学方程,完成导线运动轨迹的描述.根据树木、导线的地理信息情况,考虑导线与树木之间空间间隙绝缘特性,比较线-树绝缘特性和线路间隙击穿特性对临线树障进行预判.
2.1 计算导线风偏位移
线路旁存在树木时,在风荷载作用下输电线会发生风偏产生位移.风偏后导线距树木净空距离减小,导线距树冠绝缘间隙减小.当树木引起的空间畸变合成电场强度,大于直流输电线路间隙最小击穿电场时,则绝缘间隙被击穿,发生树闪故障.所以,首先对大风条件下,导线运动轨迹进行描述,确定导线风偏位移.在风荷载作用下,挂于绝缘子串上的导线会产生位移,如图3所示.
根据力矩平衡方程可推出导线运动角位移:

式中:Δ为导线运动角位移,℃;Pd为水平档导线风荷载,kN;Gd为垂直档导线重量,kg;Pj为绝缘子串风荷载,kN;Gj为绝缘子串重量,kg.
根据公式(12)可得导线运动线位移:

式中:x为风荷载作用下导线线位移,m;lj为绝缘子串长度,m;lx为线夹长度,m.
由公式(12)、公式(13)可建立导线风偏后动力学平衡方程,对风荷载作用下导线运动轨迹进行描述:

式中:m为单位长度导线的质量,kg/m;A为架空导线截面积,m2.
通过对公式(14)求解,可得到得在风荷载作用下导线运动线位移x,确定导线位置.
2.2 建立风偏后导线位置绝缘特性数学模型
直流输电线路的空间合成电场,由导线表面标称电场和由电晕产生的空间电荷离子流场组成[15].电荷在电场力的作用下,向极间区域移动,导致极导线与树冠之间充满了空间电荷.本文运用解析法计算±800 kV特高压输电线路极导线距树冠空间合成电场.为简化计算,假定极导线为长直线与地面平行.
2.2.1 导线距树冠空间合成电场计算
首先通过半经验公式法求解±800 kV特高压输电线路的标称电场.单极导线表面标称电场求解计算公式为

式中:E为标称电场,kV/m;V为导线对地电压,kV;H为导线距树冠高度,m;d为极导线直径,m;X为距线路中心垂直线路方向的距离,m.
根据Deutsch假设,空间电荷不影响方向只影响电场强度,计算空间合成电场:

式中:Es为导线下距树冠空间合成电场,kV/m;U为运行电压,V;ρ1为导线表面的电荷密度,C/m3;J为空间离子电流密度,A/m3;φ为无空间电荷时的空间某点电位,V;A1为导线周围合成电场强度与标称电场强度比值,kV/m;ε为真空介电常数.
2.2.2 计算直流输电线路间隙最小击穿电场
利用经验公式计算间隙的击穿电压和击穿电场强度:

式中:d为间隙距离,cm;δ为空气相对密度.
2.2.3 建立临线树障隐患预判数学模型
当导线受风荷载作用偏移后,导线距树冠空间合成电场应小于线路间隙最小击穿电场.根据式公式(17)和公式(19),可建立临线树障隐患预判数学模型为

当导线距树冠空间合成电场Es小于击穿场强Eb时,树木引起的畸变电场对导线不构成威胁.当合成电场Es大于击穿场强时Eb,导线距树冠空间绝缘间隙被击穿,易发生树闪故障,应及时对故障树进行处理.
3 仿真分析验证树障预判数学模型
本文采用Ansoft软件,对导线距树木空间畸变电场强度分布情况进行仿真分析,验证树障隐患预判模型的准确性.首先,建立导线下存在树木的二维仿真模型,如图4所示.

图4 线下树木仿真模型图

图5 二维模型网格划分
为减少软件分析计算时间,本文采用三角形单元对导线下存在树木二维模型进行网格划分.基于电场强度和误差值大小对模型中空气域的疏密划分,自适应确定网格单元分布疏密和网格大小,确保计算时每个单元计算精度相同.如图5所示,分裂导线周围网格单元密集,越靠近边界空气域网格稀疏,三角形单元网格划分提高计算精度.
根据模型对导线距树冠空间场强分布进行分析,空间电场场强分布情况,如图6、图7所示.
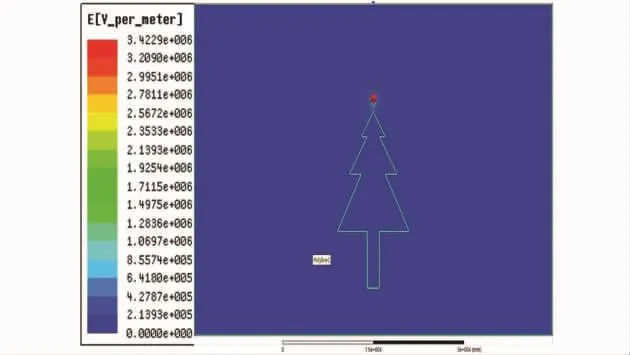
图6 导线下树木空间畸变电场分布云图

图7 导线距树冠空间畸变电场分布云图
如图8所示,从导线上方空气域边界,经过线下树冠至树根纵向空间的电场强度分布曲线.曲线中场强最高点为距空气域边界11.34 m处树冠,此时畸变电场强度为662 480.043 V/m.距空气域边界6 m处为导线位置,此处电场强度为61 170.794 7 V/m.距空气域边界11.41 m处到距空气域边界29.995 m处,电场强度为0.此段长度反应树高值,为18.591 m.综上所述,树高为18.591 m的树木畸变电场强度为662 480.043 V/m,线路间隙最小击穿电场强度为38 230 V/m,由此可得树冠处畸变电场强度远大于击穿场强,存在发生树闪故障危险,应及时处理.

图8 导线距树冠空间畸变电场分布曲线图
4 结 论
(1)根据动态应力数学模型、弧垂和应力之间的非线性数学关系、Richard树木生长高度预测方程,构建导线距树木的最小净空距离数学模型.通过与规定导线与树木之间的最小垂直距离进行比较,当最小净空距离大于13.5 m时,则存在树障隐患应及时处理.
(2)结合动力学平衡方程,确定导线受风荷载作用后风偏位置.计算树冠距导线空间畸变电场强度,构建临线树障隐患预判模型.通过比较树冠距导线空间畸变电场强度和线路间隙击穿电场强度,当空间畸变电场大于线路最小击穿场强时,则发生树闪故障.
参考文献
[1] 孔伟,朱明伟,付豪.架空输电线路导线在ANSYS中的找形分析[J].东北电力大学学报,2011,31(6):64-67.
[2] 秦力,张学礼,张杰,等.浅析500kV输电铁塔结构体系的可靠性[J].东北电力大学学报,2008,28(2):9-12.
[3] 李勇伟,周康,李力,等.±800kV 直流特高压输电线路的设计[J].高电压技术,2009,35(7):1518-1525.
[4] 祝贺,李炳坤.淮南-上海特高压工程电气不平衡度及换位方式仿真计算[J].东北电力大学学报,2017,37(4):45-51.
[5] 舒印彪,刘泽洪,袁骏,等.2005年国家电网公司特高压输电论证工作综述[J].电网技术,2006,30(5):1-12.
[6] 赵孟丹.输电线路下方生长物视频监测技术研究[D].北京:华北电力大学,2013.
[7] 冉铁军,高莹,徐子安.输电线路远程监测装置:CN201589785U[P].2010.
[8] 刘罡,杨志荣,苗利敏,等.输电线路综合在线视频监测与管理系统:CN201584816U[P].2010.
[9] 嵘刘,嵘曾,高宏宇.输电线路实时监测预警装置:CN201237823Y[P].2009.
[10] 张红先,针方,波李,等.输电线路灾情监测系统:CN101127153A[P].2008.
[11]王孔森,孙旭日,盛戈皞,等.架空输电线路导线弧垂在线监测误差分析及方法比较[J].高压电器,2014,50(4):27-34.
[12] B.Elde.Analysis of growth equations[J].For Sci,1993,39(3):594-616.
[13] B.L.Von.Quantitative laws in metabolism and growth[J].Quart Rev Biol,1957,32(3):217-231.
[14] 李凤日,吴俊民,鲁胜利.Richards函数与 Schnute生长模型的比较[J].东北林业大学学报,1993,21(4):15-24.
[15]赵畹君.高压直流输电工程技术[M].北京:中国电力出版社,2011.

