常微分方程在数学建模中的应用

覃 游

（四川师范大学附中，四川 成都 610000）

当前，常微分方程是很多理工科专业设置的一门基础课程。与微积分相似，常微分方程也是人类认识世界、改造世界不可或缺的一个数学工具。在长年累月的生产实践中，常微分方程已经演变成了数学领域对理论和实践相联系的重要分支，而利用常微分方程建立数学模型，也成为了解决很多实际问题的重要手段。因此，对常微分方程在数学建模中的应用展开探究，有着非常重要的意义。

1 常微分方程在腐败人数预测模型中的应用

当前，人们经常在电视或网络上看到很多政府官员因为腐败问题而落马的报道，而这些腐败官员的落马往往会牵扯出大量的涉案分子，这些被牵扯出来的涉案分子往往会采取东躲西藏的方式来逃避法律对他们的制裁。为此，可以用常微分方程来进行数学建模和创新，利用这些被牵扯出的涉案分子的人数来对总涉案人数加以预测，建立出一个新的腐败人数预测模型，这包括以下三个步骤。

（1）假设阶段。设t表示时间，x（t）表示这个腐败集团所牵扯的涉案分子的总人数有关t的函数，X0表示在t=0时刻这个腐败集团所牵扯的涉案分子的总人数，r（x）表示牵扯涉案分子的增长率，r表示在x0时刻牵扯的涉案分子人数的增长率，也称作固有增长率，xm表示这个腐败事件可能会牵扯的最多人数，μ表示在追查时产生的阻力系数，i（t）表示这个腐败事件所牵扯人数在总人数中的比例，λ表示在t=0时刻这个腐败事件所牵扯人数在所有人数中的比例，λ表示已被抓到的每个腐败分子在每个月之内所招供出的平均人数。

（2）分析阶段。若已牵扯出的腐败分子人数呈现出了递增趋势，就说明潜在的腐败分子人数正在逐渐减少。x（t）表示这个腐败事件牵扯的人数与时间t之间的函数关系，x（t）是与t有关的连续函数，其中的一个上界是xm，牵连人数对应的增长率r（x）和x（t）之间也存在特定的函数关系。从前面的假设可知，r（x）是x的一条线性函数。r（x）=r-kx（k表示斜率，k＞0）。当x=xm时，涉案人数的增长率是0，r（xm）=0，这样就能确定k=r/xm，那么所牵扯的涉案人数的增长率函数就能够用r（x）=r（1-x/xm）来加以计算。

（3）计算阶段。在不考虑侦察的力度以及侦查的困难程度可能给侦查结果带来影响的情况下，可以建立出以下的微分方程：

解得

在考虑侦查的困难程度可能给侦查结果带来影响的情况下，可以将阻力系数设为μ，从而建立出以下的微分方程：

di/dt=λi（1-i）-μi

i（0）=i0（λ≠μ）

解得

这个数学模型可以作为我国的反腐败部门在今后的反腐败工作当中对腐败分子牵连的人数进行预测的方法，不难发现，在理论上计算出的腐败人数与实际工作当中所查出的腐败人数有着非常近似的误差范围。

2 常微分方程在生物种群数量模型中的应用

（1）研究背景。目前，生物种群的数量问题是一个非常热门的问题，这个问题引起了世界范围内众多专家和学者的广泛关注。想要对某个生物种群在未来的数量进行预测，主要的影响因素就是这一生物种群在目前的总数目，以及这一生物总群在未来一段时间内的增长情况和其所处环境的影响因素。当某一生物的种群数目增加到一个特定的程度之后，这一种群的生物就并将在狭小的生存空间中相互竞争，并且种群中各个生物的增长状况会在种群数目不断增加的状况下出现削减。因此，对该生物种群在未来的数目，就可以通过建立生物种群数量模型的方式来解决。

（2）Malthus模型。如果想对未来一段时间中该生物种群的总体数目进行推测，那么所涉及到的主要特征就是数学刻画，即该生物的自然增长率，这是确定该生物在一段时间内种群的增量和种群的数量之间比例系数的有效手段，同时还能反映出在一段时间内，该生物中某个单个个体的平均增加量，其自然增长率既能作为常数，又能作为变数。

可以用t表示时间，用常数λ表示该生物种群所对应的自然增长率。假设在该生物种群所生存的环境下，只存在这一种生物种群，或其它的生物种群的存在不会对该生物种群的生存造成影响。在t时刻，该生物种群的数量可以表示为N（t），但是N（t）的数量是非常庞大的，所以可将其视作时间t的连续可微函数。假设在t=0的时刻，这个生物种群的数量用N0来表示，那么在△t这一时段内，该生物种群数量的净增加量就可以用t垣△t时刻该生物种群的数量减去t时刻该生物种群的数量来计算出来，其常微分方程为：

N（t垣△t）N（t）=λN（t）△t

根据这个常微分方程，可以建立出Malthus模型：

dN（t）/dt=λN（t）

N（0）=N0

解得 N（t）=N0eλt

从这个结果可以看出，上面所建立的数学模型在结果上是和19世纪之前欧洲各大地区统计出的人口数据完全吻合的。另外，从这个方程还可以得知，在一些地广人稀的地区，其人口的增长情况更加符合这种模型，并呈现出指数增长的趋势，这就证明这种假设与数学建模的方式是非常合理的。

（3）蕴ogistic模型。在使用Malthus模型的过程中，人们发现，Malthus模型对于19世纪之后的人口统计数据与实际相比存在着较大的差异，这就表明Malthus模型在应用上是有一定的局限性。随着生物种群的数量在不断地增加，外界的自然资源和环境等因素对各种生物种群数量所产生的阻滞作用也愈发突出，也就是说，Malthus模型当中所提出自然增长率的合理性并不是在任何情况中都适应的。为此，可以对其加以创新，将其改进为蕴ogistic模型。

在蕴ogistic模型中，可以假设某种生物种群所对应的自然增长率与其种群数量的函数关系为f（N），并用Nm表示该生物种群所在的环境能够容纳的最大数量。在进行数学建模时，通常要将未知函数的处理过程表示为线性函数或二次函数的形式，可以假设f（N）=ax垣b是这一线性函数，那么由f（Nm）=0可知，f（N）=λ（1-N/Nm）。将其改进为logistic模型：

dN/dt=λ（1-N/Nm）N

N（0）=N0

解得

利用这一模型与10世纪到20世纪的美国人口统计数据进行对比，可以发现两者是完全吻合的，这就证明蕴ogistic模型能够合理地表示出生物种群的数量在外界环境制约下出现的变化情况。

3 常微分方程在人口预测模型中的应用

由于地球上的资源存在有限性的特点，所以世界上的各个国家都已经开始有计划地对人口的增长情况进行控制。想要建立准确的人口预测模型，就必须先弄清楚影响人口增长的因素有哪些。实际上，影响人口增长的因素非常多，如自然出生率、自然死亡率、人口迁移、战争、自然因素等等，如果在初始阶段就对所有的因素都加以考虑，那么模型的建立就会无从下手。因此，可以先对问题进行简化，建立出一个较为粗糙的数学模型，然后再对其进行逐步地修改，从而得到一个相对完善的数学模型。

1838年，荷兰著名的数学家韦尔侯斯特将常数Nm引入到了数学建模中，并用其表示自然环境能够容许的最大人口数。一般而言，一个国家的工业化水平越高，这个国家的生活空间就越大，Nm也就越大。韦尔侯斯特假设，增长率可以表示为r（1-Nt/Nm），而净增长率则会随着Nt的增大而逐渐减少，当Nt逐渐趋近于Nm时，净增长率则会逐渐趋近于零，利用这一假定就能够建立出人口预测模型。所以，可以利用韦尔侯斯特的理论进行创新，建立出一个新的人口预测模型。

dN/dt=r（1-N/N0）N

N（t0）=N0

这个常微分方程建立出的数学模型是一种逻辑模型，可以对其进行分离变量处理，其解为：

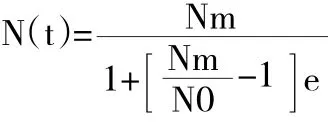
根据这个人口预测模型，并结合韦尔侯斯特的相关理论，就能够对人口的增长情况进行合理的预测了。

4 结语

综上所述，文章主要对常微分方程在数学建模中的应用进行了详细的分析，并对一些以往的数学模型进行了改进，并利用常微分方程创新性地设计出了一些新的数学模型，并将其应用在了不同领域的问题研究当中。希望广大的数学领域的专家和学者们能够对常微分方程在数学建模中的应用展开更加深入的研究，创造出更多的数学模型，从而解决社会上的一些复杂课题。

参考文献

［1］李宝萍.常微分方程在数学建模中的应用［J］.赤峰学院学报（自然科学版），2012，28（21）：1-2.

［2］方芳.常微分方程理论在数学建模中的简单应用［D］.合肥：安徽大学，2010.

［3］谷成玲.常微分方程在数学建模中的应用［J］.数学学习与研究，2016，（3）：89.