完备Brouwerian格上矩阵方程的极大解问题
黄新宇,岳 芹
(皖西学院 金融与数学学院,安徽 六安 237012)
1 预备知识
讨论完备Brouwerian格上∧-→型矩阵方程极大解的存在问题。先给出相关概念。
定义1.1设(P,≤)是一个偏序集,a∈P,若对∀x∈P,只要x≥a,就有x=a,则称a是P的一个极大元。
定义1.2如果格L满足:对∀a,b∈L,满足a∧x≤b的最大元x存在,则称L为完备Brouwer格,记该最大元为a→b。
下面是一个Brouwer格的例子。
例1.1①设N为非负整数构成的集合,a,b∈N,定义a≤b当且仅当a|b,则(N,≤)是一个完备格,其中a∧b=g.c.d{a,b},a∨b=l.c.m{a,b},g.c.d与l.c.m分别表示a与b的最大公因子与最小公倍数。再定义a→b=l.c.m{x∈N:a∧x≤b},则L=(N,∧,∨,≤)是一个Brouwer格,0与1分别是L的最大元与最小元。
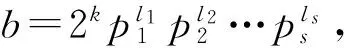
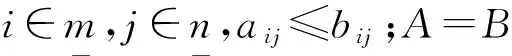
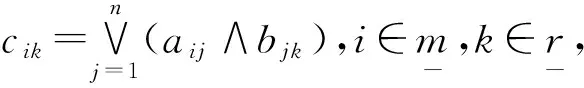
下面所讨论的格L,如无特殊说明,均指完备Brouwer格L。
L上的∧-→型矩阵方程有以下三种基本类型②:
第一类:已知A=(a1,a2,…,an),b∈L,确定X=(x1,x2,…,xn)T使
A*X=b
(1.1)
成立。记χ°={X:A*X=b}。
第二类:已知A=(aij)m×n,B=(b1,b2,…,bm)T,确定X=(x1,x2,…,xn)T使
A*X=B
(1.2)
成立。记χ1= {X:A*X=B}。
第三类:已知A=(aij)m×n,B=(bik)m×r,确定X=(xjk)n×r使
A*X=B
(1.3)
成立。记χ2= {X:A*X=B}。
2 三类方程有解的充要条件及其它们之间的关系
引理2.1[1]方程(1.1)有解,即χ°≠φ当且仅当AT°b∈χ°,且对∀x∈χ°,x≥AT°b。这里AT°b=(a1∧b,a2∧b,…,an∧b)。
为了引入下面的引理,先引入一个记号。
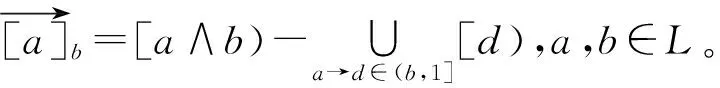

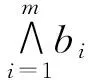



证明:(1)显然成立,下证(2)。
充分性显然,仅证必要性
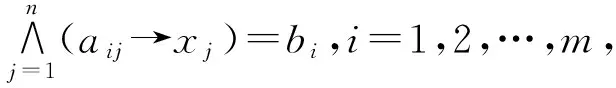




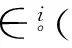
方程(1.3)等价于r个无关的方程[4]
A*(x1k,x2k,…,xnk)T=(b1k,b2k,…,bmk)T,
k=1,2,…,r

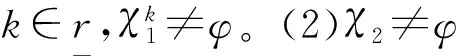
证明:显然。
3 极大解的存在情况
我们已经在有解的情况下,给出了L上∧-→型矩阵方程的最小解的表达式,如果对方程的每一个解还能找到一个大于等于它的极大解,则方程的整个解集便可完全确定。但下面这个例子说明了L上∧-→型矩阵方程的解集即使非空,对于方程的每一个解也不一定能找到一个大于等于它的极大解。
例3.1设L是如例1.1中的完备Brouwerian格,A=(0,0),b=3,则对方程(1.1)的每个解X,并不都能找到一个极大解X*,使得X*≥X。
证明:显然X=(6,9)T是方程(1.1)的解。假设存在极大解X*=(x1,x2)T,使得X*≥X,则有 (0→x1)∧(0→x2)=3,所以x1=3a,x2=3b,其中a,b为自然数,且(a,b)=1。因为(a,b)=1,6|3a,所以b必为奇数。这样 (2a,b)=1。所以(2x1,x2)=3(2a,b)=3,从而X**=(2x1,x2)T∈χ°,且X*>X,与X是χ°的极大元矛盾。
4 方程(1.1)有极大解的充要条件[5]
本节在χ°非空时,给出L上方程(1.1)的每一个解都存在一个大于等于它的极大解的充要条件。先给出如下的引理。




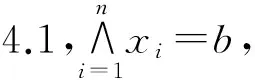

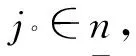
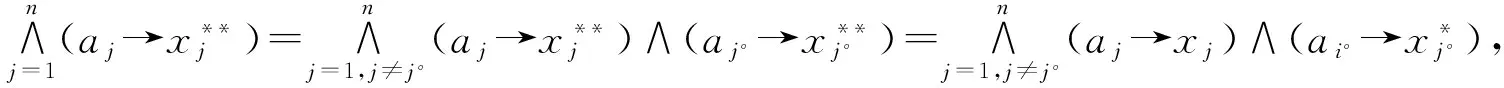
定理4.2如果χ°≠φ,X∈χ°,则存在χ°的一个极大元X*满足X*≥X的充要条件是存在L的有限子集B满足
高校腐败“一查一串一抓一窝”,怎么破?高校是人民教育之圣堂,高校职务犯罪社会危害性尤为严重。对此,遏制高校腐败泛滥,要加快推进高校廉政建设,加强思想政治教育和法纪教育,打牢拒腐防变思想基础。淡化高校行政色彩,降低或削弱行政人员拥有资源支配的权力。强化权力制约,要把对高校领导干部的监督制约落实到权力运行各环节,营造“风清气正、崇廉尚实、遵纪守法、干事创业”的高校政治生态和育人环境,办好新时代党和人民满意的高等教育。
(1)∧B=b,其中∧B表示B中所有元素的交;(2)∀p∈B,若p≠1,则b≠∧(B/{P});


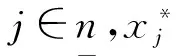
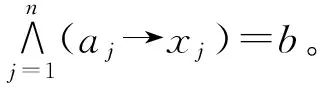
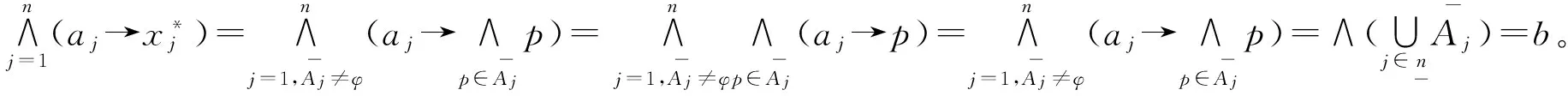
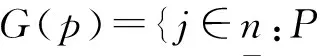



5 方程(1.2)有极大解的充要条件
由命题2.2,定理4.2,直接可推出下面定理成立。

并且根据定理4.2的证明和命题2.2,我们可以求出所有大于等于X的极大元。
注释:
①当a=0时,a→b=b;当a≠0时,a→b=0。
②第一类⊆第二类⊆第三类。
参考文献:
[1]李裕梅,王平.完备Brouwerian格上无限@-Fuzzy关系方程的极大解问题[J].四川师范大学学报(自然科学版),2003,26(3):232-235.
[2]张诚一,党平安.基于∨-·运算的F关系方程的摄动问题[J].高校应用数学学报(A辑),2002,17(2):243-247.
[3]Yi-Jia Tan. Eigenvalues and Eigenvectors for Matrices over Distributive Lattices [J]. Linear Algebra and Its Applications, 1998(283): 257-272.
[4]岳芹.关于完备Brouwer格上∧-→型矩阵方程[J].福州大学学报,2003,31(4):279-283.
[5]李裕梅.完备Brouwer格上@-Fuzzy关系方程的一些研究进展[J].模糊系统与数学,2002(16):215-217.

