债务定价、股权定价与总资产定价 ——贴现率难题的统一解模型

张志强

(中国人民大学 商学院，北京 100872)

一、引言

财务和金融活动通过投资和融资决策引导资源流向、支持经济发展，也就是通过创新推动理论的发展，应用理论提升决策的科学性和合理性。投资和融资决策的根本依据是资产价值，计算资产价值的基本方法是折现现金流(DCF)方法，而贴现率是应用DCF方法的关键变量。因而贴现率在财务和金融以至经济活动中扮演着核心和重要的角色。比如，投资决策中公认最合理的净现值(NPV)方法，其合理性即以正确估计贴现率为前提。

资本资产定价旨在探讨各种资本的合理价格，也就是各种资本资产的合理收益率或贴现率。所谓资本资产，具体表现为债务资本、股权资本以及总资本。债务资本从投资者角度看也就是债权，如果债权人是银行则为贷款；股权资本包括上市公司的股票和非上市公司的股权；总资本则是公司中债务资本与股权资本之和。因此，资本资产定价在财务和金融领域居于核心地位，相关研究受到理论和实务界普遍重视。

资本资产定价问题至今没有得到解决，具体表现为无法恰当考虑风险以确定各种资本资产的贴现率，而且存在偏颇和错误认识。张志强等[1]考虑全部风险的资本资产定价模型(ZZ CAPM)在这方面有所创新，成为本文研究的理论基础；另外，最优资本结构研究方面的突破提供了ZZ破产成本模型[2]，成为本文研究的得力工具。基于这两个基础性突破，经过严谨的逻辑和定量推导，本文得出了债务资本、总资本和股权资本的三个贴现率模型。

本文的贴现率模型用两种不同的推导方法相互印证，体现出严谨性和科学性。而且，所得到的模型都是封闭解，便于实践中应用。这三个贴现率模型弥补了财务和金融的理论断层，有原创性贡献。这种根本性的理论突破意味着广泛的应用价值，现实中各种投融资问题，包括银行、保险、证券、价值评估等实务领域的核心业务，都可以借助这些模型提升分析与决策的科学性与合理性。

二、文献综述

(一)研究文献

夏普CAPM(1964)[3]发表之后，学术领域掀起了用市场数据检验资本资产定价模型的热潮。有的数据检验结果与模型相符，有的数据检验结果与模型不相符。于是，有些学者尝试增加模型中的系数的个数，将模型扩展为多因素模型,以获得更好的解释市场数据的能力。较早的有罗斯(1976)提出的套利定价理论(APT)[4]。APT认为，股票的收益受到两类变量的影响，第一类是宏观经济的影响，具体会有若干影响变量；第二类是公司相关事件的影响，通常归结为噪音因素。选定影响变量即自变量，基于一套数据进行统计分析，每个变量赋予系数并加入常数项，就可以得到APT的具体模型。

受APT的启发，学术领域热衷于寻找新的影响因素，这种努力持续到现在。如Urteaga等[5]研究了行业之间波动率风险溢价的差异，Maio(2016)[6]研究了行业间收益差异对股权风险溢价的影响，Luo等[7]研究了股票期望收益与未来波动性的关系。在这类研究中，较为突出的是法玛和弗伦奇的研究。他们发现上市公司的市值、账面市值比、市盈率可以更好地解释美国股票收益率的差异，并发表了Fama-French三因子模型(1993)[8]。后来又加入盈利性和投资两个因素，发表了五因子模型(2015)[9]。最近，法玛等[10]又用北美、欧洲和亚太地区的数据对其五因子模型进行了测试，得出模型在不同地区的适用性差异。三因子模型在证券投资领域有重要影响，有不少追随研究，较新的研究如Clarke等(2017)[11]。

中国学者也积极参与到资本资产定价的研究中。杨朝军等[12]对上海股票市场研究发现，股本规模、可流通股占总股本的比例、净资产收益率和成交量也是影响股票收益的重要因素。何治国(2001)[13]研究发现，市盈率倒数(E/P)和账面/市值价值比(BV/MV)也对股票收益有很强的解释能力。类似地，贾权等[14]研究发现，股票系数与其收益率呈现负相关关系，而流通市值、市盈率、账面/市场价值的比率对于收益率也有很强的解释能力。吴世农等[15]研究发现，中国股市存在显著的“价值效应”，期望收益与公司规模呈反向关系。陆静等[16]以及陈清等[17]研究中国股市流动性与股票预期收益的关系，构建了流动性调整下的CAPM 模型(LCAPM)。朱顺泉(2010)[18]基于上交所数据分析得出，市场平均超额收益率与系统风险之间存在正相关关系，与非系统风险不存在显著的线性关系，基本符合标准形式的CAPM。张矢的等[19]构建了“未充分分散投资下的资本资产定价模型”，并且基于中国A 股市场数据的检验，初步显示出模型的有效性。田存志等[20]总结了国外关于股票市场及其特征的研究，王化成等[21]探讨了企业战略差异与权益资本成本的关系。

(二)研究偏差

可以理解，贴现率是有关投融资决策的标准和依据；作为标准或依据，应该有唯一性和正确性。因此，贴现率的研究是要树立标准，而不是描述或解释现象。可惜，CAPM之后的研究往往忽略了这一点，想通过市场数据验证模型或通过模型解释现象；而市场数据虽然有客观性，但却没有唯一性和正确性。即便模型得到(某套)数据的验证，也不代表模型有普适性，更不代表有唯一性和正确性。近年来，也有学者产生过怀疑，如Fabian等[22]以及Li(2017)[23]等。

研究方向的偏差加上其他原因，导致贴现率问题至今没有得到解决，贴现率的确定也存在一些误解或错误。一个表现是，按照流行的理解，贴现率在概念上混同为资本成本。因此，一种流行的方法是按照资本的机会成本或加权平均成本确定贴现率。机会成本是另一个项目的(预期)收益率，与考察或评估项目的风险不相关；而公司资本的加权平均成本在任何决策时点只有一个，显然无法分别匹配若干备选项目的风险。

另一个表现是，按照流行的模型，估计贴现率时只考虑系统风险，而不是全部风险。在夏普CAPM之前，没有一个可以与投资对象风险相联系的贴现率模型。但业内公认，贴现率应该与投资风险相联系；而且应该包含时间补偿和风险补偿。夏普的CAPM恰好有“无风险利率+风险补偿率”的合理结构，其中，无风险利率代表对时间延迟的补偿，风险补偿率代表对投资风险的补偿。因此，模型一经问世，便引起轰动，学界和业界都争相学习、传播和应用。后来，夏普也因为这个成果获得诺贝尔奖。夏普CAPM为：

ri= r +i(rm-r)

(1)

其中，ri为第i种证券的合理收益率，自然也是第i种证券的适用贴现率。

r为无风险利率，按照惯例，可以按照同样期限的国债收益率来确定。

rm为市场所有证券平均的收益率。因而，(rm-r)代表市场平均的风险补偿率，而i(rm-r) 代表第i种证券的风险补偿率。

但此后不久人们就发现，该模型有一个致命的缺陷，就是只考虑了系统风险，而假定非系统风险因为组合投资而完全分散掉。也就是说，夏普CAPM只考虑了系统风险的补偿。这意味着，式(1)所表达的是“贴现率=无风险利率+系统风险补偿率”，或者“贴现率=无风险利率+部分风险补偿率”。

只考虑系统风险也就是没充分考虑风险，或低估了风险。因此，运用夏普CAPM计算(某项目或资产的)贴现率，并据以进行决策就违背了决策的谨慎原则。而且在现实中，实业投资往往是单一或少数项目的投资，很少有风险分散的效果。即便在证券投资领域，也很难达到充分分散风险的程度，没有投资可以完全不承担非系统风险。这意味着，夏普CAPM作为贴现率模型，既缺乏理论上的合理性，也不符合决策的实际情况。

为理论上自圆其说，对于夏普CAPM的缺陷，学术界有若干解释。比如，一种解释是，因为理论上公司的股东可以通过分散投资而将非系统风险完全分散掉，所以市场只承认系统风险；即使公司投资某项目冒了全部风险，市场也只补偿系统风险。不难明白，在投资决策中，问题不是市场给予多少风险补偿，而是管理者或决策者究竟需要考虑全部还是部分风险做出决策。显然，无论市场给不给全部补偿，都应该考虑全部风险，而不是视而不见地只考虑系统风险就做出投资决策。

(三)新的突破

贴现率在财务和金融中居于核心和不可或缺的地位。夏普CAPM之后，关于贴现率的研究并没有停止，近年来如Smith[24]、Straehl[25]等。但多数研究存在理解上的偏差，没有充分理解财务和金融学科面向未来的决策特性，专注或侧重于解释过去的现象，因此也就一直没有发现或建立更全面考虑风险的贴现率模型。在这种情况下，实践只能原地踏步，Berk等[26]的研究也证实了这一点。

张志强等[2]纠正了破产成本概念理解和计量方法的错误，推导出了破产成本模型，进而推导建立了最优资本结构模型。可以理解，其中破产成本模型提供了计量破产风险影响的定量方法，从而有希望为确定债务资本的贴现率提供工具。

张志强等[1]纠正了有关贴现率与资本成本概念上的混乱，推导建立了考虑全部风险的资本资产定价模型(ZZ CAPM)。这是夏普CAPM以来贴现率研究的新突破；同时，这也许预示着贴现率研究全面突破的开始。有了正确的概念基础和基本的定量基础，就有了在概念和定量上全面推进贴现率确定理论与方法的希望。

ZZ CAPM考虑全部风险计算总投资的贴现率，现实中的投资具体化为股权、债权以及总投资。可以理解，同一投资对象(如一家公司)的股权、债权以及总投资的贴现率应该不同，因为投资者所冒的风险不一样。所以，贴现率的确定最终应该具体落实到股权、债权以及总投资的贴现率模型上。

三、债务资本的贴现率

1974年，Merton就探讨了债务资本的合理收益率或适用贴现率[27]。然而，这个研究的理论与应用价值一直没有得到足够的认识和探讨。我们研究发现，基于ZZ破产成本探讨债务资本的贴现率，在概念和逻辑上更便于理解和推导。

(一)ZZ破产成本模型

破产成本与资本结构决策相联系。学术研究之所以至今没能解决最优资本结构问题，关键原因之一是没能跨越破产成本定量这个障碍。张志强等[2]取得了研究突破，推导出了破产成本模型，进而推导建立了最优资本结构模型。ZZ破产成本模型为：

BC=XN(-d2)-SN(-d1)

(2)

式(2)中，BC 代表破产成本；S代表公司目前价值；X代表企业债务的本金，按照研究惯例，它也是债务的现值；N(-d2)和N(-d1)分别代表标准正态分布中变量值取-d2和-d1时的累积概率。其中，d1和d2可分别按式(3)和(4)求得。

(3)

(4)

(二)ZZ债务资本贴现率模型

不考虑交易成本，债务资本投资的合理收益率即是债务资本的贴现率，应该也是贷款的合理利率。用X表示无风险债务的当前价值；在考虑风险的情况下，设c为债务的年风险补偿率；T为债务到期时间，则有风险债务的价值为Xe-cT。另一方面，有风险债务的价值等于相应无风险债务的价值减去破产成本。因此：

Xe-cT= X-[XN(-d2)-SN(-d1)]

(5)

根据式(5)不难求得风险补偿率c。

e-cT=1-[N(-d2)-(S/X)N(-d1)]

=1-N(-d2)+(S/X)N(-d1)

=N(d2)+(S/X)N(-d1)

上式两边取自然对数，则有，

-cT=ln{N(d2)+(S/X)N(-d1)}

(6)

公司的债务比率可以定义为L=X/S，则S/X=1/L，从而，

c=-ln[N(d2)+N(-d1)/L]/T

(7)

其中，对照式(3)和(4)，

(8)

(9)

式(7)即是由ZZ破产成本模型推导出来的贷款或债务资本的风险补偿率模型。在此基础上，加上无风险利率，就是债务资本的贴现率模型，为方便区别和称谓，不妨称为ZZ债务资本贴现率模型，也可以称为ZZ贷款利率模型[28]。即：

y=r-ln[N(d2)+N(-d1)/L]/T

(10)

根据式(8)、(9)和(10)，债务资本的贴现率取决于无风险利率r、债务期限T、公司价值波动率以及公司债务比率L四大因素。

可喜的是，1974年Merton推导出的债务资本风险补偿率模型与式(7)完全一致[6]，只不过当时没有ZZ破产成本模型，推导过程更为复杂难懂。应该明白，严格逻辑可以跨越时空而成立，不会随时间、地点、条件而不同。所以经由不同逻辑过程得到同样结论是最难得也是最有说服力的证明，可以看作是最终证明，因为这说明结论有唯一性和正确性。由此判断，ZZ债务资本贴现率模型的正确性已经得到证实。

代入典型数据可以测试ZZ债务资本贴现率模型。如，假设无风险利率、债务到期时间和公司价值波动率分别为r=4%、T=5、=26%。当公司负债率即债务资本占公司总价值的比率分别为40%、50%、60%、70%、80%、90%时，根据模型计算，债务资本的贴现率分别为4.44%、4.93%、5.59%、6.38%、7.26%、8.21%。随着公司负债率的增加，违约风险逐渐增大，债务资本的贴现率也逐步上升，初步说明模型有合理性。

中国银行业利率市场化政策已经到位，这意味着银行业竞争的加剧，对银行的定价能力提出了新的挑战。由于银行贷款即是公司的债务，ZZ债务资本贴现率模型显然可以应用于银行贷款利率的确定，这个模型在银行贷款决策上的应用还有若干问题值得探讨[28]。

四、总资本的贴现率

张志强等运用期权定价方法[1,29]，推导得出了考虑全部风险的资本资产定价模型，即全风险贴现率模型或ZZ CAPM。模型的形式为：

(11)

经过数年探讨，我们又找到新的推导方法，即由ZZ债务资本贴现率模型推导ZZ CAPM，而且这个推导过程更为简单，ZZ CAPM的正确性因此也得到证实。

一般认为，在总资本中，债务资本承担较小的风险，而股权资本承担较大的风险。其实，这个结论是就单位资本而言的。就全部资本而言，随着债务资本比率的增加，债务资本承担的总风险将越来越大。到极端情况，即债务资本比率达到100%时，必然是全部风险都落到债务资本上。这种情况下债务资本也就是总资本，而债务资本的合理收益率也就是总资本的合理收益率。换言之，令债务比率L=100%，基于式(8)-(10)，就应该得到总资本的合理收益率或贴现率。

根据式(8)和式(9)，当L=100%时，lnL=0，因而，

(12)

将式(12)以及L=100%代入式(10)，则有

y =r-ln[N(d2)+N(-d1)/L]/T

=r-ln[N(d2)+N(-d1)]/T

(13)

不难看出，式(13)所表达的正好是ZZ CAPM即式(11)。与原推导[5]相比，新推导简单很多。当然，原推导并不作废，两个推导正好可以相互印证；而且原推导过程中得到的风险当量、确定当量以及约当系数模型都是难得且有理论和应用价值的成果。

五、股权资本的贴现率

前面已经推导出了债务资本和总资本的贴现率模型，而且都有两种推导方法相互印证。在此基础上，如果总资本的贴现率等于股权资本贴现率与债务资本贴现率的加权平均数，就可以根据这三者关系求解股权资本的贴现率了。既然总风险由股权人(股东)和债权人分担，可以认为，无论股权和债务资本的风险如何变化，它们的和即为总风险。根据贴现率与风险相对应，总风险补偿率就应该等于股权资本和债务资本风险补偿率的加权平均数，从而总贴现率就应该等于股权资本和债务资本贴现率的加权平均数。

进一步，随着债务比率的变化，总风险进而总贴现率是否保持不变呢？如果总贴现率保持不变，则意味着公司或资产总价值不变，即资本结构不影响公司或资产价值。也许有人认为这个问题已经得到解答，即MM模型I证明了资本结构不影响公司价值。但是，MM模型I的假设前提明显不符合实际，其中关键假设是没有公司所得税也没有破产风险。从解决难题的需要考虑，这样的假设无可厚非，因为只有先简化前提才有可能有所发现。但基于这样的假设推出的结论不是最终结论，不能直接应用。

根据张志强等[2]的研究，公司的确存在最优资本结构，但通过优化资本结构获得的价值增值非常有限。就正常公司而言，债务资本的利弊即节税收益和破产成本的价值都很小，两者相互抵消后，对公司价值的净影响就微乎其微了。从数量上讲，与零负债的情况相比，多数公司通过优化资本结构获得的价值增值不到公司价值的1%。

既然正常情况下资本结构对公司价值的影响微弱，实际决策又有非精确性，这种微弱的影响在推导中就可以忽略不计。因此，可以假定资本结构不影响公司价值；进而可以假定，总资本的贴现率保持不变且等于股权资本与债务资本贴现率的加权平均数。

用k表示总资本贴现率，ke表示股权资本贴现率，kd表示债务资本贴现率。根据上面的分析，k为ke和kd的加权平均数。设kd的权重为L，则ke的权重为(1-L)。kd即为前面ZZ债务资本贴现率模型中的y。因此有：

k=(1-L)ke+Lkd

(14)

ke=(k-Lkd) / (1-L)

(15)

将式(10)和(11)代入式(15)，

(16)

式(16)即是求股权资本合理收益率或贴现率的模型，可以称为ZZ股权资本贴现率模型。其中，d1和d2可按式(8)和(9)计算。

可以看出，ZZ股权资本贴现率模型也是一个封闭解，有无风险利率加风险补偿率的完美结构，只是风险补偿率的表达略微复杂一些；模型显示，股权资本的贴现率或合理收益率与公司债务比率正相关，即会随着公司负债率的提高而提高。

六、基本应用演示

考虑风险确定贴现率是财务和金融理论的核心，相关理论进展意味着对许多问题的理解和决策都可以得到大幅度的改进。下面用一个投资决策的例子演示一下本文的模型对财务和金融问题的解答和解决能力。

例：三个投资主体角度的净现值计算

传统上投资决策最合理的标准是净现值，即净现值大于零可以投资。但有关计算往往得到单一的净现值。在人们的想象中，它是项目总体的净现值。其实，净现值可以也应该分别从项目整体以及股权和债务资本投资者角度计算。目前业界流行的算法，没有区分这些角度，只不过是一个笼统或角度不清的净现值。可以理解的是，之所以会有角度不清的计算，原因之一是没有方法确定各个投资主体的适用贴现率。现在，有了三个ZZ贴现率模型，区分投资主体计算净现值就具备可行性了。

假设Y项目初始投资为300万元，投资当年就可运营获利，预计寿命周期10年内的息税前收益如表1所示。寿命周期内每年计提折旧20万元，寿命周期结束时项目无残值。已知资本市场上10年期的年无风险利率为4%，项目收益率波动率估计为20%。初始投资的300万元中，银行贷款为120万元，股权资本为180万元。公司根据项目现金流量情况，与银行商定贷款期限为7年，利率为8.8%，每年年末付息，到期还本，不再续借新债。该项目的适用所得税率为25%。另外，假定该项目自负盈亏，不牵扯公司其他项目。请评价该项目投资的可行性，并进一步分别从银行和股东角度评价其投资的可行性。

根据前面提供的信息，列表计算债务、股东和整个项目角度的净现值，如表2所示。

表1 Y项目收益期望值(单位：万元)

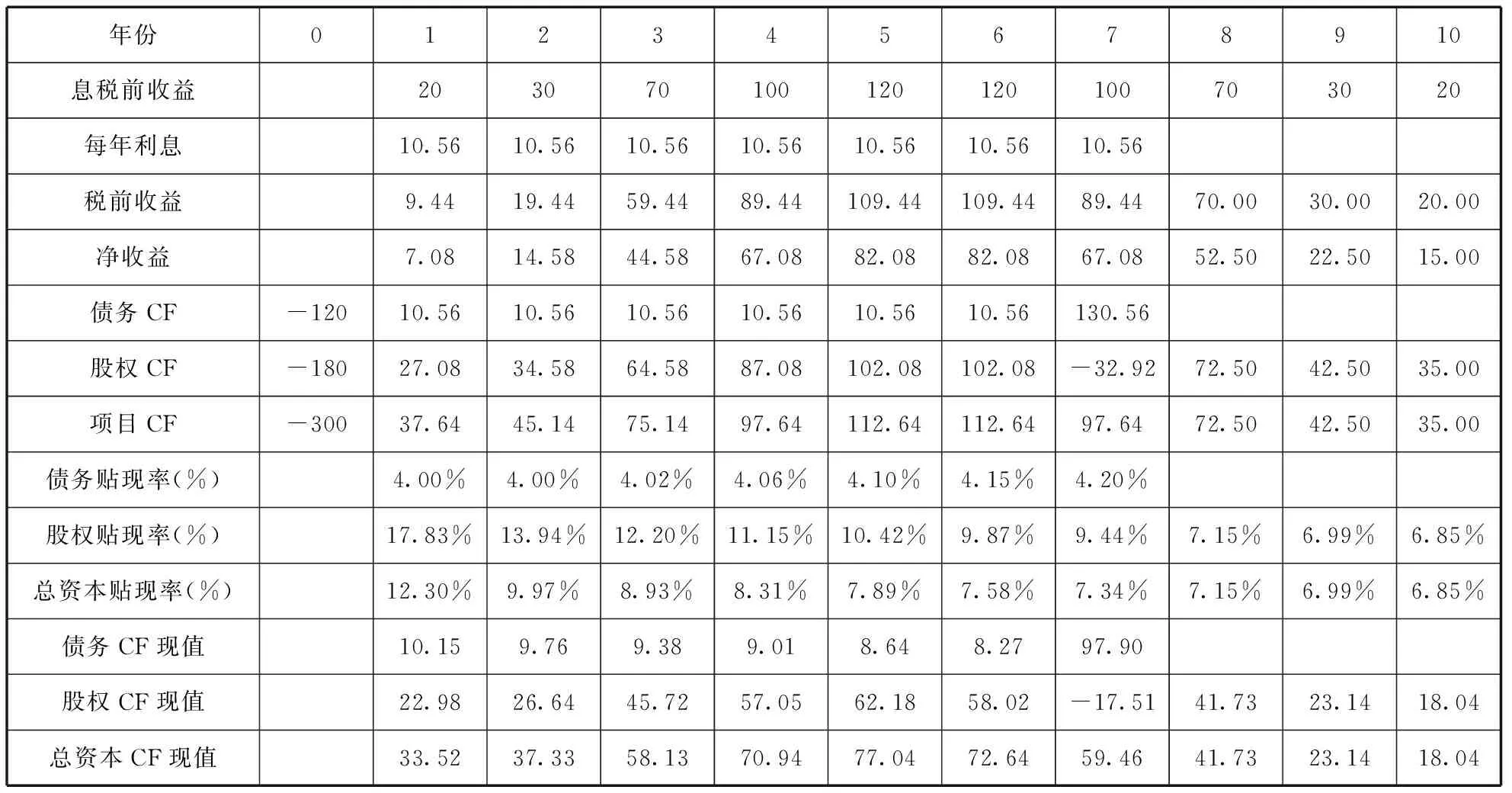
表2 Y项目收益期望值与现值(除贴现率外，单位：万元)

注：CF指现金流量。在最后三年即第8、9、10年，因为银行贷款的本息已经全部归还，支持该项目的资本全部为股权资本。因此，股权资本的适用贴现率与全部资本相同。

表2最后三行为债务、股权和总资本各年现金流量的现值；各自加总得到债务、股权和总资本投资收益的总现值分别为153.11万元、337.99万元、491.96万元；各自减去初始投资(120万元、180万元和300万元)得到债务、股权和总资本角度的投资净现值分别为33.11万元、157.99万元、191.96万元。由于从银行、股东和项目整体角度看，投资的净现值都大于0，所以，各投资主体都可以获得价值增值，项目可行。

这里，债务、股权角度的投资净现值之和不等于总资本角度的净现值，有约0.86万元的差异。造成这个差异的主要原因是，总资本贴现率是债务资本和股权资本贴现率的加权平均数，其中的权重应该是市场价值下的权重，但按市场价值计算权重又牵扯到若干细节问题，此处就简单取账面价值比重作为权重了。

七、结论与建议

总资本以及股权和债务资本的贴现率一直是财务和金融领域的难题。本文在理清相关概念的基础上，得出了三个资本资产定价模型，对贴现率难题进行了全面透彻的解答。可以看出，这些模型至少有三方面的优势：(1)从模型的形式到模型中的变量，都经过严谨逻辑推理得出，极少有作者的“设计”或“假设”，排除了主观因素的影响。(2)三个模型基于同一起点即破产成本，在逻辑上相互贯通；推导过程都有两种方法相互印证，可以确保模型的确定性、唯一性和正确性。(3)模型的推导过程简单，最终形式都是封闭的模型，便于理解、学习和应用。应用这些模型，企业的投融资决策分析，银行的贷款决策以及有关保险、担保、证券和价值评估的从业实践，都可以进行更为科学合理的计算、分析，得到更为可靠的结论。

十九大后我国经济和金融改革将进一步向纵深发展，本文关于资本资产定价的探讨发现至少可以在以下几个方面起到推动作用。

(1)商业银行可以借助ZZ债务贴现率模型改进贷款审批和利率确定决策。利率市场化改革在宏观政策上已经到位，但微观实体还习惯于原来的做法，多数银行没有理论上过关的贷款审批和利率确定模型。深入研究可以发现，在增量意义上应用ZZ债务贴现率模型，既可以得出合理的贷款利率，又可以得出合理的审批界限，有助于银行的贷款决策，目前主观加经验的决策标准很难达到这样的合理性与精准性。

(2)投资银行也可以借助ZZ债务贴现率模型改进债券产品设计和利率确定，有关债券利率、期限等要素的设计，都可以从该模型中找到理论依据。证券公司以及有关基金可以借助ZZ股权和总资本贴现率模型优选股票和优化投资组合，因为贴现率代表合理收益的标准，以此为标准，将更容易从风险收益权衡的角度判断各个证券的优劣。

(3)各种工商业企业可以在战略调整、投资融资活动中应用本文的贴现率模型更好地进行事先评估。比如，可以更正原来净现值计算的错误，分别从项目总体以及股权和债权投资者角度评估投资的可行性，增加投资评估结果的信息含量并增加信息的透明度，从而提高决策的正确性，促进资本和资源在行业之间的流动和合理配置。

(4)政府监管可以利用本文的贴现率模型改进项目审批等方面的标准，从而更好地把控资源的流向和更好地发挥市场机制的正面作用，在提升宏观调控精准度的同时，增强微观主体的活力。西方国家一直讨论不清楚从长期政策考虑贴现率应该递增、递减还是不变[30]，ZZ CAPM对这个问题做了清晰明确的解答，即贴现率在长期中应该递减；而且这个递减的下限为无风险利率。

(5)担保公司和保险公司可以利用ZZ破产成本模型改进产品设计与定价，也可以借助这些模型开发新产品。制约金融创新的重要瓶颈往往是定价能力问题。中国担保公司和保险公司的基本定价方法是行业惯例和经验统计，缺少专业理论与方法的支撑，没有在长期实践中培养起定价能力。包括ZZ破产成本模型在内的有关模型可以支持或辅助有关风险的定价，在担保公司和保险公司的应用潜力巨大。

(6)各类金融公司都可以借助本文的贴现率模型建立更为科学合理的业绩评价标准，从而改进业绩考核，因为贴现率即是与风险相匹配的合理收益率。依据这样的标准评价有关金融工作的业绩，必然有助于评价的合理性与公平性，从而才能真正发挥业绩考核促进业务发展，增强微观单位活力的作用。

参考文献：

[1]张志强, 俞明轩. 贴现率与资本成本：如何确定贴现率[J]. 财经问题研究，2014(12)：11-17.

[2]张志强,肖淑芳. 节税收益、破产成本与最优资本结构[J]. 会计研究，2009(4)：47-55.

[3]William F. Sharpe. Capital asset prices: A theory of market equilibrium under conditions of risk [J]. Journal of Finance, September 1964, 19(3): 425-442.

[4]Stephen A. Ross. The arbitrage theory of capital asset pricing [J]. Journal of Economic Theory, 1976, 13(3): 341-360.

[5]Ana González-Urteaga, Gonzalo Rubio. The cross-sectional variation of volatility risk premia [J]. Journal of Financial Economics, 2016, 119(2): 353-370.

[6]Paulo Maio. Cross-sectional return dispersion and the equity premium[J]. Journal of Financial Markets, 2016, 29: 87-109.

[2]Xingguo Luo, Jin E. Zhang. Expected stock returns and forward variance [J]. Journal of Financial Markets, 2017, 34: 95-117.

[8]Eugene F Fama, Kenneth R French. Common risk factors in the returns on stocks and bonds [J]. Journal of Financial Economics, 1993, 33(1): 3-56.

[9]Eugene F Fama, Kenneth R. French. A five-factor Asset pricing model [J]. Journal of Financial Economics, 2015(116): 1-22.

[10]Eugene F Fama, Kenneth R. French. International tests of a five-factor asset pricing model [J]. Journal of Financial Economics, 2017, 123: 441-463.

[11]Roger Clarke, Harindra de Silva, Steven Thorley. Fundamentals of efficient factor investing [J]. Financial Analysts Journal, 2016, 72(6): 9-26.

[16]杨朝军, 邢 靖.上海证券市场CAPM实证检验[J]. 上海交通大学学报，1998(3)：59-64.

[17]何治国.中国股市风险因素实证研究[J]. 经济评论，2001(3)：81-85.

[14]贾 权, 陈章武.中国股市有效性的实证分析[J]. 金融研究，2003(7)：86-92.

[15]吴世农, 许年行.资产的理性定价模型和非理性定价模型的比较研究——基于中国股市的实证分析[J]. 经济研究，2004(6)：105-116.

[16]陆 静, 李东进.基于流动性风险的证券定价模型及其实证研究[J]. 中国软科学，2005(12)：145-150.

[17]陈 青, 李子白.我国流动性调整下的CAPM 研究[J]. 数量经济技术经济研究，2008(6)：66-78.

[18]朱顺泉.资本资产定价模型CAPM 在中国资本市场中的实证检验[J]. 统计与信息论坛，2010(8)：95-99.

[19]张矢的, 高明宇, 吴 斌.未充分分散投资下的资本资产定价模型：基于中国A 股市场的实证检验[J]. 管理评论，2014(10)：24-37.

[20]田存志, 程富强, 付 辉.关于金融市场长记忆性研究的若干争论[J]. 经济学动态，2016(6)：141-150.

[21]王化成, 张修平, 侯粲然, 等.企业战略差异与权益资本成本——基于经营风险和信息不对称的中介效应研究[J]. 中国软科学，2017(9)：99-113.

[22]Fabian Baetje, Lukas Menkhoff. Equity premium prediction: Are economic and technical indicators unstable [J]? International Journal of Forecasting, 2016, 32(4): 1193-1207.

[23]Jiahan Li, Ilias Tsiakas. Equity premium prediction: The role of economic and statistical constraints [J]. Journal of Financial Markets, 2017, 36: 56-75.

[24]Simon C. Smith. Equity premium estimates from economic fundamentals under structural breaks [J]. International Review of Financial Analysis, 2017, 52: 49-61.

[25]Philip U Straehl, Roger G Ibbotson. The long-run drivers of stock returns: Total payouts and the real economy [J]. Financial Analysts Journal, 2017, 73(3): 32-52.

[26]Jonathan B Berk, Jules H van Binsbergen. How do investors compute the discount rate? They use the CAPM [J]. Financial Analysts Journal, 2017, 73(2): 25-33.

[27]Robert C Merton. On the pricing of corporate debt: The risk structure of interest rates [J]. Journal of Finance, 1974, 29(2): 449-470.

[28]张志强.贷款定价的基本模型[J]. 中国资产评估，2017(4)：26-30.

[29]Fischer Black, Myron Scholes. The pricing of options and corporate liabilities [J]. Journal of Political Economy, 1973, 81(3): 637-654.

[30]刘昌义, 何 为. 不确定条件下的贴现理论与递减贴现率[J]. 经济学家，2015(3)65-73.