基于Pearson相关系数的快速虚拟网格匹配定位算法
郝德华,关维国,邹林杰,焦 萌
(辽宁工业大学 电子与信息工程学院,辽宁 锦州 121001)
0 引言
全球定位系统[1]在室外环境可以精确定位,但在复杂的室内环境中定位效果并不理想,甚至无法定位,因此产生了多种基于无线信号(蓝牙、WiFi等)的短距离室内定位技术。蓝牙4.0容易部署、功耗低且大多智能设备都具有蓝牙功能,所以基于蓝牙4.0的室内定位技术备受学者推崇。而在室内定位方法的研究中,基于接收信号强度指示(Received Signal Strength Indicator, RSSI)的定位方法是最常用的方法之一,该方法因其不需额外添加硬件、低能耗、实现比较简单等优点,成为定位技术的研究热点[2]。基于RSSI的室内定位方法又主要分为基于RSSI测距的几何定位算法和基于RSSI建库的位置指纹定位算法[3]。
无线信号在复杂多变的室内环境中传播易受墙壁、地板及行人等的阻挡而产生反射、折射及绕射影响[4],使各信标节点产生不同的信号衰减,从而影响定位精度。基于RSSI测距的定位算法利用理论或经验传播模型将RSSI转成距离进行定位[5],但模型拟合和参数选择会影响定位精度。如张鹏等[6]提出一种基于RSSI测距的高次消去最小二乘解算算法,但算法定位精度依赖于测距精确度且计算复杂度较高;基于RSSI建库的位置指纹定位算法有较高的定位精度,如RADAR系统和Horus系统,均采用基于RSSI指纹建库进行定位[7],然而,建立离线数据库的工作量很大,室内定位环境复杂多变,在实际应用中存在很大的局限性。文献[8]在离线阶段构建RSSI位置指纹地图,对实时接收的RSSI和指纹地图中的RSSI值求其相关特性并据此定位,但需要建立离线指纹数据库,离线阶段建库工作繁杂。王艳丽等[9]也提出了利用相关性匹配位置指纹库的定位方法,定位精度较高,但同样需要建立位置指纹库,离线工作量很大。Wang等[10]提出了基于距离和RSSI之间相关性的网格定位算法(CORRelation, CORR),在非视距(Non Line Of Sight, NLOS)环境下利用该算法对路径损耗指数进行实时修正,并根据几何算法实现最终定位估计。
针对测距算法定位精度受模型影响较大以及位置指纹匹配定位算法离线建库工作量大的缺点,本文在现有的利用相关性进行定位研究的基础上,提出一种基于Pearson相关系数的快速虚拟网格匹配定位算法PCC(Pearson Correlation Coefficient)。利用Bounding-Box方法[11]依据信标节点ID(Identification)及通信半径R确定初始虚拟网格划分区域,并对其进行快速迭代细分;计算虚拟网格中心点到各信标节点距离的对数所构成向量L;依据接收信号强度Pr向量和L向量之间的Pearson相关系数在网格区域内遍历寻优确定待定位节点的位置。为提高定位精度,选取Pearson相关系数接近于-1的k个近邻坐标并以Pearson相关系数为权值加权最优估计待定位节点位置,从而使定位结果更加精确。最重要的是,本文算法无需离线指纹建库,大大节省了定位工作量。
1 RSSI传播特性分析
定位系统由待定位节点(蓝牙终端设备)和多个iBeacon信标节点构成。终端设备在定位区域可收到各iBeacon信标节点发射的信息数据,包括通用唯一识别码(Universally Unique Identifier, UUID)、Minor(识别区域内不同信标节点单号)、Major(识别不同区域的区域号)、RSSI、物理(Media Access Control, MAC)地址[9]。
在基于RSSI的定位过程中,待定位信标节点接收到各iBeacon信标节点的RSSI值和ID,计算出路径损耗,然后利用损耗模型将其转换成伪距估计值;但实际环境中,信号传播会受到影响,使伪距估计值出现误差并上下波动,从而影响定位精度。近年来室内定位主要的传播路径损耗模型有:自由空间传播模型、Motley模型、华为路径损耗模型、对数正态路径损耗模型等[12],本文选用贴近于室内信号路径损耗的华为模型并对其修正,其传播损耗模型为:
PL=20 lg(f)+Nlg(d)+Pf(m)-28+Xσ
(1)
其中:PL表示信号传播损耗值;f为信号的传播频率(MHz);N=10n,其中n为衰落因子,取值为2.5~3.0;Pf(m)为楼层穿透因子系数,在半开放室内环境下Pf(m)=6+3(m-1),在较为封闭的环境Pf(m)=15+4(m-1);同一楼层时m取值为1。参数经验修正值为28 dBm;Xσ为高斯正态分布的随机分布变量。
同一楼层空旷会议室视为半开放环境,测距利用华为室内路径损耗修正模型,信标节点发射功率为Pt(dBm),根据式(1),可得在待定位节点处接收的RSSI参数Prssi为:
Prssi=Pt-PL=Pt-20 lg(f)-10nlg(d)-6+28-Xσ
(2)
对上式进行简化,令:
A=Pt-20 lg(f)-6+28
(3)
则可得距离d与Prssi之间的相关特性如式(4)所示:
Prssi=A-10nlg(d)-Xσ
(4)
2 Pearson相关的快速虚拟网格定位
待定位节点接收各信标节点发送的ID和RSSI,算法首先对RSSI值进行预处理,以RSSI优化估计值参与最终定位估计。基于Pearson相关系数的快速虚拟网格定位利用遍历寻优进行匹配定位,若定位区域较大,在整个定位区域进行虚拟网格划分会造成迭代次数增加,定位时延增大。故本文先以Bounding-Box算法缩小并确定初始虚拟网格区域;然后再迭代细分虚拟网格,以虚拟中心到各信标节点距离的对数与RSSI求相关系数进行匹配定位。
2.1 RSSI信号预处理
实际测试中会发现无线信号在室内传播时大部分RSSI值会在理论值附近上下波动,但总会有一小部分RSSI值会严重偏离理论值,直接对RSSI取平均参与定位可能会导致误差较大,为了得到更精确的RSSI值,对信号进行预处理。
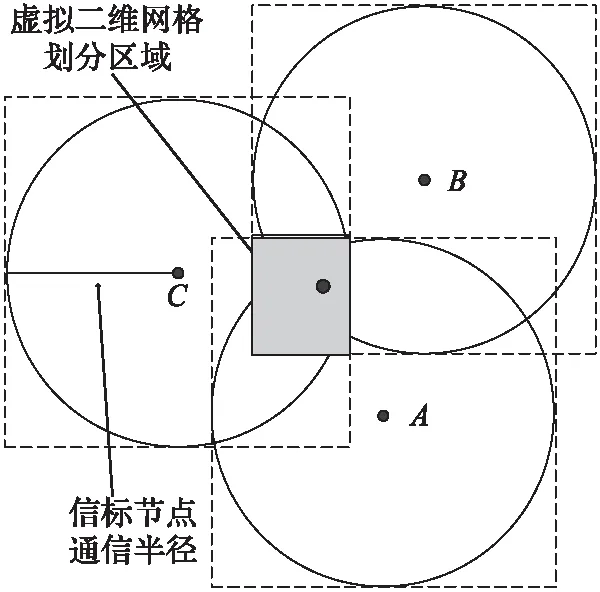
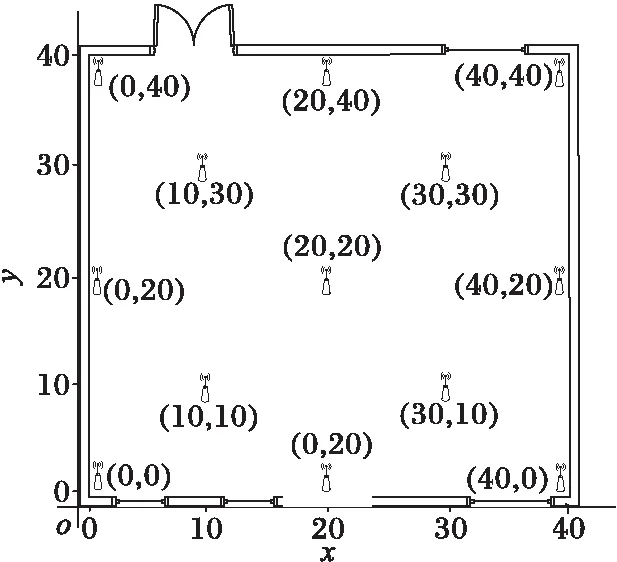
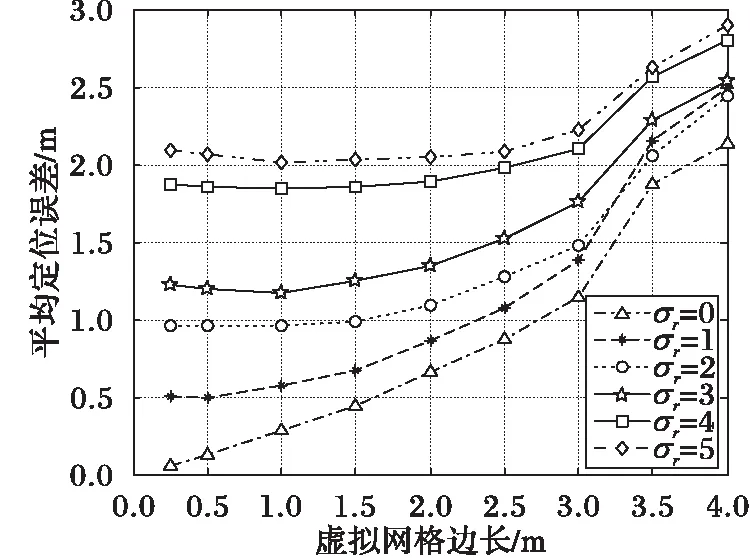
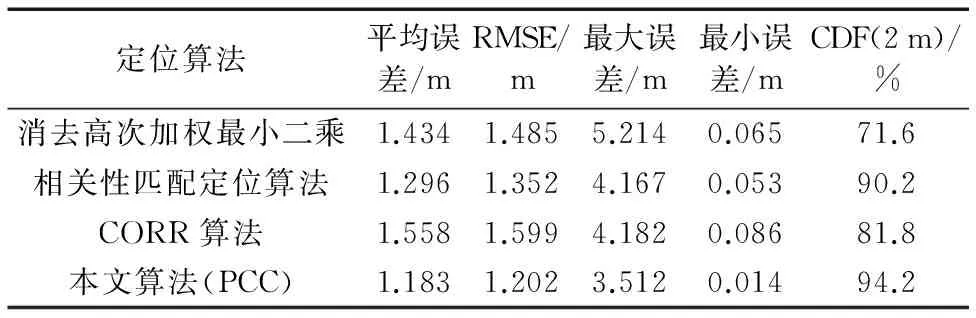
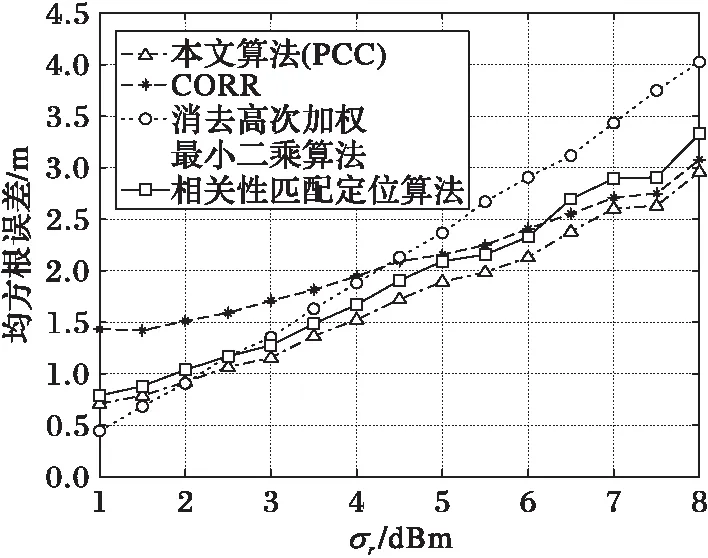
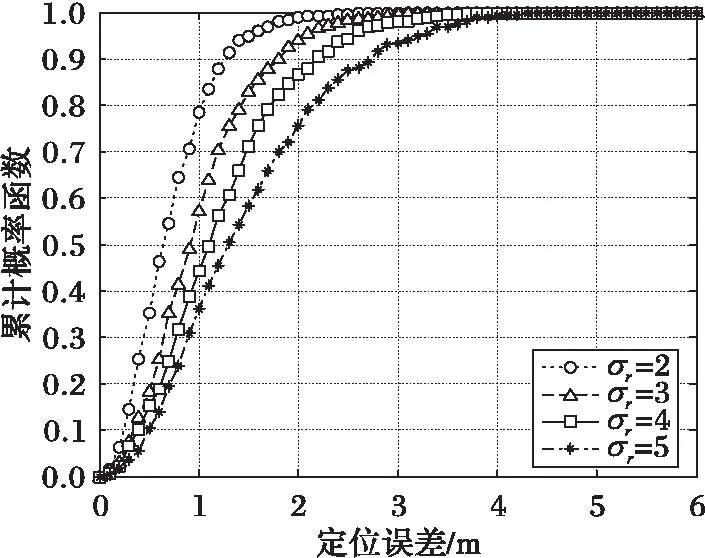
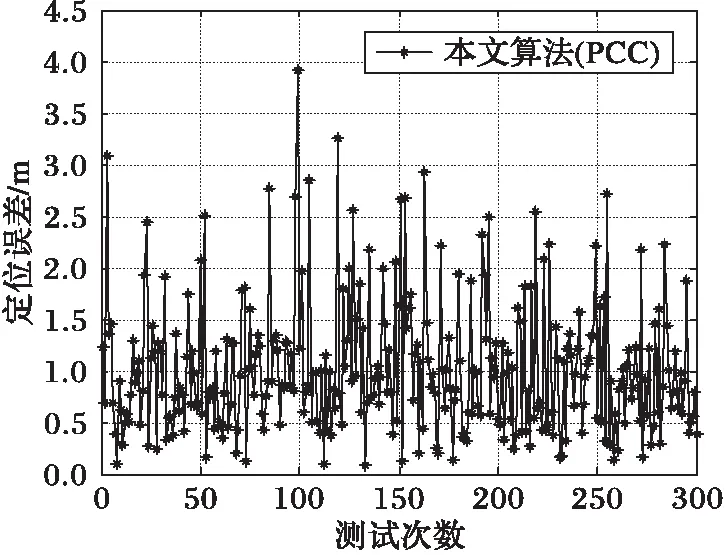
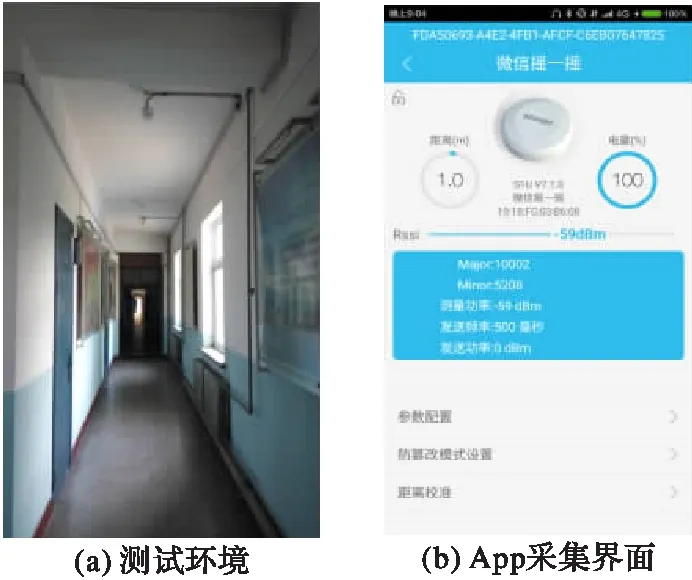
设在整个定位场景部署有Q个iBeacon信标节点,待定位节点可接收到M(M (5) 其中: (6) (7) 选择RSSI高概率发生区即RSSI值出现概率较大的区域,经大量实验分析选择以σ规则设立置信区间,则临界概率为0.68时最佳:0.68≤f(Pi)≤1。滤波后RSSI取值范围为[μ-σ,μ+σ],对区间内的RSSI值进行计算,求其几何平均值,即可得到最终参与定位的RSSI优化估计值。 为了减少算法计算量,提高基于Pearson相关系数的匹配定位算法速率。首先以Bounding-Box算法确定初始虚拟网格划分区域,减小虚拟网格划分区域。图1所示为Bounding-Box方法示意图,设待定位节点在iBeacon信标节点A、B、C的通信半径范围内,以各信标节点坐标为圆心,信标节点的通信距离为半径画圆,则各圆外接正方形得交叠区域为一个矩形(如图中灰色部分),即定义此矩形区域为初始的虚拟网格划分区域。 Bounding-Box核心思想是:在定位场景内待定位节点可以接收到M个iBeacon信标节点的ID、RSSI值以及通信半径R,信标节点坐标为Xi=(xi,yi),其中i=1,2,…,M。依据信标节点的位置ID及通信半径R,可得待定位节点所在的矩形区域,即为虚拟网格划分区域,则该虚拟网格划分区域的左下角坐标(xmin,ymin)和右上角坐标(xmax,ymax),由式(8)计算得: (8) 进而可得虚拟网格划分区域可以表示为: (9) 依据上述Bounding-Box方法以邻居信标节点的坐标确定虚拟网格划分区域,待定位节点必定处于这个矩形区域中,从而可以在很大程度上缩小待定位节点可能存在的区域。以该区域再进行虚拟网格划分,可大大减少定位算法的计算量,加快匹配定位速率,从而达到实时定位的效果。 图1 Bounding-Box方法 Fig. 1 Bounding-Box method 在统计信号处理研究领域,相关性研究一直受到学者们的关注。对于相关性的研究即是利用相关的两组变量来反映整体关联性的方法[9,13]。Pearson相关系数又称积矩相关,表示两组变量的相关程度。其相关系数公式为: (10) 其中:X,Y表示两组长度相等的向量,ρX,Y范围为[-1,+1]。当值为0,两组向量无关;当值在[-1,0),两组向量负相关;当值在(0,+1],两组变向量正相关。相关系数的绝对值越接近于1,表示相关程度越高。 (11) 在待定位节点所在区域,选取一个已知点,则可直接计算各邻居iBeacon信标节点与该点之间的距离,计算所得距离值向量为D=[d1,d2,…,dM]。根据RSSI传播模型分析可得Pr和D是相关的两组向量,又根据式(4)可见,Prssi和lg(d)相关性更贴近于信号传播模型规律,因此其相关性应比Prssi和d的相关程度更高,并且对数函数严格单调,lg(d)随着d变化而单调变化,所以利用Prssi和lg(d)进行定位会有更准确的相关性体现,所以本文算法将距离d转换成其对数的形式即: li=lg(di) (12) 则可得距离对数向量L=[l1,l2,…,lM],即可得到关于已知位置点到各iBeacon信标节点的距离对数矩阵: (13) 若在定位区域内选取多个已知点,则基于Pearson相关系数的定位估算方法即分别计算定位区域内选取的各已知节点与各信标节点之间的Pr向量和L向量之间的相关程度。根据式(4)表现出的相关特性可以看出,Pr向量和L向量呈负相关特性。两向量负相关性越高,则已知点越接近于待定位节点,其计算公式可由式(10)推导出: (14) 若是假设的已知点就是待定位节点,在无噪声环境下,其Pearson相关系数值越接近于-1(甚至等于-1),定位点越接近于待定位节点,定位精度越高,从而完成定位估计。 1)在整个定位区域部署Q个iBeacon信标节点,每次选取M个参与定位(M 2)利用Bounding-Box算法根据ID及通信半径R确定并缩小虚拟网格划分区域,取该矩形区域最小边长的1/4作为初始虚拟网格的边长。每次迭代细分可以得到T个虚拟网格,各个虚拟网格中心的坐标为Xi,t=(xi,t,yi,t),其中t=1,2,…,T;i=0,1,2,…。i为快速迭代次数。 3)求解各虚拟网格中心到待定位点的距离对数向量Lit=[li1,li2,…,liM]。对Pr向量和Lit向量分别求解Pearson相关系数ρ并从小到大进行排序可得集合ρi={ρi,1,ρi,2,…,ρi,t,…,ρi,T}。 5)更新网格边长mi+1=mi/2。在噪声条件下虚拟网格迭代划分时会出现不规则区域,若直接以不规则区域外接矩形进行下一次迭代会造成计算重复而增加计算量。故本文迭代算法直接对虚拟网格中心坐标进行迭代细分,则第i+1次虚拟网格划分所得的网格中心坐标为: (15) 6)判断虚拟网格边长是否小于设定边长阈值。若小于则转入7)输出结果,否则转到步骤3)循环。 7)通过Pearson相关系数加权得到坐标估计值为: (16) 为分析本文PCC算法性能,定位仿真实验环境选取一个长宽为40 m×40 m会议室环境。整个定位区域均匀部署13个iBeacon信标节点,iBeacon信标的广播发射功率均设置为0 dBm;具体信标布置场景如图2所示。 图2 室内定位仿真环境 Fig. 2 Indoor localization simulation environment 本文iBeacon信标节点通信半径均为25 m;在定位阶段终端设备对个信标节点均采集10次。在空旷的会议室环境中,经实验采集验证,路径损耗指数拟合值为2.6,定位噪声Xσ基本服从0均值、标准差为3 dBm的高斯噪声。 本文PCC算法中网格迭代划分依据和虚拟网格边长的更新速度共同影响算法的定位精度与定位效率,为选取合适的迭代参数,在不同迭代参量条件下对算法进行定位仿真实验可得结果如表1所示,可以看出以二分法(size(ρi)/2)为划分依据且以mi+1=mi/2进行网格边长更新时,定位时间最长且定位效果较差;而以四分法(size(ρi)/4)为划分依据且以mi+1=mi/4进行网格边长更新时,定位时间最短但定位误差较大。故综合表1数据,本文选取四分法(size(ρi)/4)为划分依据并以mi+1=mi/2进行网格边长更新。 表1 不同迭代条件下PCC算法性能对比Tab. 1 Performance comparison of PCC algorithm under different iteration conditions 虚拟网格划分边长阈值是PCC算法一个重要参数,理论上边长阈值越小,算法定位精度越高,但在噪声条件下,网格细分到某一阈值后将无法继续提高定位精度,反而增加定位计算量。为选定合适边长阈值,本文针对不同噪声条件对算法进行定位仿真分析,算法定位误差随边长阈值变化情况如图3所示。低噪情况下,定位精度随边长阈值减小而提高;在标准差为2~5 dBm的显著噪声条件下,当边长阈值小于1时,算法定位误差趋于平缓,定位精度不在随边长阈值减小提高,因此本文将边长阈值选定为1 m。 图3 定位误差随边长阈值变化 Fig. 3 Positioning error changes with length threshold 在典型室内环境下(RSSI噪声σr=3 dBm),将本文PCC算法与消去高次加权最小二乘法、CORR、相关性匹配定位算法进行定位仿真对比,本文算法以3.2节选定为参数进行定位仿真实验,可得定位性能对比如表2所示。本文算法的定位误差小于2 m的累计分布函数(Cumulative Distribution Function, CDF)概率为94.2%,其定位均方根误差(Root-Mean-Square Error, RMSE)为1.202 m,比消去高次加权最小二乘法、CORR、相关性匹配定位算法分别提高0.283 m、0.397 m和0.150 m。定位精度优于其他三种算法;虽然定位精度比相关性匹配定位算法仅提高了0.150 m,但无需建立数据库,大大减少了采集工作量,降低了定位成本,更容易应用推广。另外根据表2中定位最大定位误差值和最小定位误差值可见,PCC算法比其他算法定位稳定性较高。 表2 不同定位算法性能对比Tab. 2 Performance comparison of different localization algorithms RSSI噪声标准差的大小会影响信标节点的定位精度。为测试本文PCC算法的抗噪性能,在噪声标准差从1 dBm变化到8 dBm的条件下,选取500个随机位置点对各算法进行定位仿真实验,各算法均方根误差随噪声标准差变化情况如图4所示,可见不同噪声标准差下PCC算法的定位均方根误差小于其他算法。当σr=2 dBm时,PCC算法、CORR、相关性匹配定位算法和消去高次加权最小二乘法定位均方根误差分别为0.918 m、1.510 m、1.030 m和0.923 m。在σr=7 dBm的恶劣环境下,PCC算法的均方根误差可保持为2.592 m;CORR的均方根误差为2.769 m;相关性匹配定位算法的均方根误差为2.894 m;而消去高次加权最小二乘法的均方根误差则为3.484 m。可见本文PCC算法相对于其他算法具有更好的抗噪性能。 图4 不同噪声下各算法定位均方根误差对比 Fig. 4 Comparison of positioning RMSE of each algorithm under different noises 在RSSI噪声标准差分别为2~5 dBm变化条件下,对本文PCC算法进行500次蒙特卡罗定位实验。定位误差累积分布函数CDF曲线如图5所示。当噪声标准差σr=2 dBm时,定位精度优于2 m的概率可达到98.7%;当噪声标准差σr=4 dBm,定位精度在86.6%概率下优于2 m;在噪声标准差σr=5 dBm的恶劣环境下,定位精度仍可保证在75.6%概率下优于2 m。所以PCC算法有较高的定位精度和良好的鲁棒性。 为验证本文PCC算法的环境适用性能,仿真环境二选取一长宽为30 m×3 m的室内走廊,在该环境中均匀部署6个iBeacon信标节点,由于环境宽度限制,网格划分边长阈值设置为0.5 m,其余参数设置均与3.1节仿真环境相同,考虑信号的反射、折射等多径影响以及行人的遮挡,走廊环境实测统计后噪声标准差约为3 dBm。在定位区域内随机选取300个待定位节点求定位误差,可得其定位估计误差如图6所示,PCC算法的平均定位估计误差为1.141 m。 图5 定位误差的累积概率分布 Fig. 5 Cumulative probability distribution of positioning error 图6 定位估计误差 Fig. 6 Positioning estimation error 室内定位测试实验选取学校教三楼二楼走廊环境,长宽为20 m×2.4 m,测试环境如图7(a)所示。在两侧墙壁上均匀部署6个寻息科技S1U型信标节点,信标天线高度2.3 m,使用红米手机为接收设备采集信号进行定位,信号采集App界面如图7(b)所示。 图7 室内定位测试 Fig. 7 Indoor positioning test 在测试环境中选取5个定位点进行测试分析,在固定位置使用红米手机连续接收6个信标节点的信号强度,每个位置点对各信标节点均采样10次,采样间隔为500 ms。测试得接收信号强度和定位结果如表3所示,可见实际测试定位误差与图6仿真的平均定位误差基本一致,故本文PCC算法在实际定位中也可达到相同的定位效果。 表3 待测位置点的测试定位误差Tab. 3 Test positioning error of points to be measured 本文针对位置指纹匹配定位算法离线采集建库工作量大的缺点,提出一种基于Pearson相关系数的快速虚拟网格匹配定位算法。算法计算RSSI向量与各虚拟网格中心点到各信标节点的距离对数向量之间的Pearson相关系数,并据此进行匹配定位估计;同时采用Bounding-Box方法确定初始虚拟网格区域,并以快速迭代的形式进行网格细分,从而保证了定位算法的计算效率,以达到实时定位的效果。通过仿真及实验表明,本文算法不仅具有优于位置指纹匹配定位算法、CORR算法和消去高次加权最小二乘算法的定位精度和稳定性,更重要的是,虚拟网格无需建库采集指纹,克服了位置指纹匹配定位算法因建立离线指纹库工作量大而难以推广应用的缺点,同时比CORR算法的定位速率更高,能够满足室内实时定位的需求。在后续的研究工作中,将开展该算法在动态环境下连续定位估计问题的研究。 参考文献(References) [1] MANNUCCI A J, WILSON B D, YUAN D N, et al. A global mapping technique for GPS-derived ionospheric total electron content measurements [J]. Radio Science, 2016, 33(3): 565-582. [2] DENG Z, YU Y, YUAN X, et al. Situation and development tendency of indoor positioning [J]. China Communications, 2013, 10(3): 42-55. [3] 乐志伟,王浩,谢小军.基于RSSI障碍势能矫正的定位算法[J].电子测量与仪器学报,2017,31(2):200-207.(LE Z W, WANG H, XIE X J. Localization algorithm based on RSSI obstacles potential energy correction [J]. Journal of Electronic Measurement and Instrumentation, 2012, 9(2): 52-65.) [4] 毕京学,甄杰,郭英.室内定位无线接收信号强度测距模型的研究[J].导航定位学报,2014,2 (4):8-10. (BI J X, ZHEN J, GUO Y. Indoor positioning range based model of the received signal strength [J]. Journal of Navigation and Positioning, 2014, 2(4): 8-10.) [5] 周艳.基于RSSI测距的传感器网络定位算法研究[J].计算机科学,2009,36(4):119-120.(ZHOU Y. Study of wireless sensor network localization algorithm based on RSSI [J]. Computer Science, 2009, 36(4): 119-120.) [6] 张鹏,周建国,冯欣,等.接收信号强度测距法无线室内定位解算方法研究[J].测绘科学,2014,39(4):13-16.(ZHANG P, ZHOU J G, FENG X, et al. RSSI ranging based wireless indoor positioning solutions [J]. Science of Surveying and Mapping, 2014, 39(4): 13-16.) [7] 关维国,鲁宝春.基于二维网格融合特征参数的室内匹配定位算法[J].计算机应用,2014,34(9):2464-2467.(GUAN W G, LU B C. Indoor matching localization algorithm based on two-dimensional grid characteristic parameter fusion [J]. Journal of Computer Applications, 2014, 34(9): 2464-2467.) [8] SUN Y L, XU Y B. Error estimation method for matrix correlation-based Wi-Fi indoor localization [J]. Ksii Transactions on Internet & Information Systems, 2013, 7(11): 2657-2675. [9] 王艳丽,杨如民,余成波,等.相关性匹配蓝牙信标位置指纹库的室内定位[J].电讯技术,2017,57(2):145-150.(WANG Y L, YANG R M, YU C B, et al. Indoor localization of bluetooth beacon position fingerprint based on correlation algorithm [J]. Telecommunication Engineering, 2017, 57(2): 145-150.) [10] WANG R, FENG J. Grid-based correlation localization method in mixed line-of-sight/non-line-of-sight environments [J]. Ksii Transactions on Internet & Information Systems, 2015, 9(1): 87-107. [11] 张乙竹,李雅晴,周礼争,等.基于自适应RSSI的Bounding-Box轮回选择WSN定位算法[J].计算机应用究,2016,33(9):2767-2768.(ZHANG Y Z, LI Y Q, ZHOU L Z, et al. Bounding-box recurrent selection algorithm for WSN based on self-adapted RSSI [J]. Application Research of Computers, 2016, 33(9): 2767-2768.) [12] 刘云,刘菁原.基于RSSI的加权质心定位算法优化研究[J]. 华中师范大学学报(自然科学版),2016,50(3):358-362.(LIU Y, LIU J Y. Optimization research on weighted centroid localization algorithm based on RSSI [J]. Journal of Huazhong Normal University (Natural Sciences), 2016, 50(3): 358-362.) [13] 胡晖,许浩峰,包伟华.基于相关性算法的超声波回波定位[J].自动化仪表,2015,36(10):96-98.(HU H, XU H F, BAO W H. Ultrasonic echo location based on correlation algorithm [J]. Process Automation Instrumentation, 2015, 36(10): 96-98.) This work is partially supported by the Directional Program of Liaoning Province Natural Science Foundation (20170540437). HAODehua, born in 1992, M. S. candidate. His research interests include mobile communication and wireless technology. GUANWeiguo, born in 1973, Ph. D., professor. His research interests include mobile network positioning, ubiquitous network wireless positioning. ZOULinjie, born in 1991, M. S. candidate. Her research interests include mobile communication and wireless technology. JIAOMeng, born in 1990, M. S. candidate. Her research interests include communication technology and application engineering.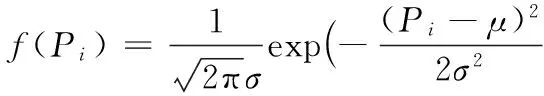
2.2 Bounding-Box确定虚拟网格划分区域
2.3 基于Pearson相关的定位估算方法
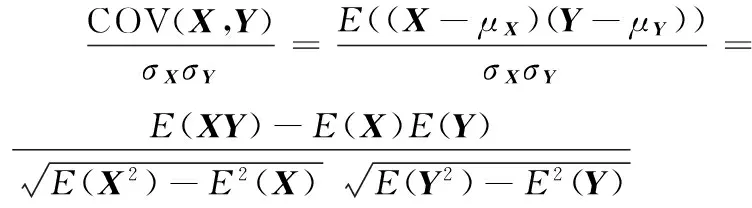
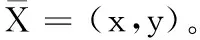
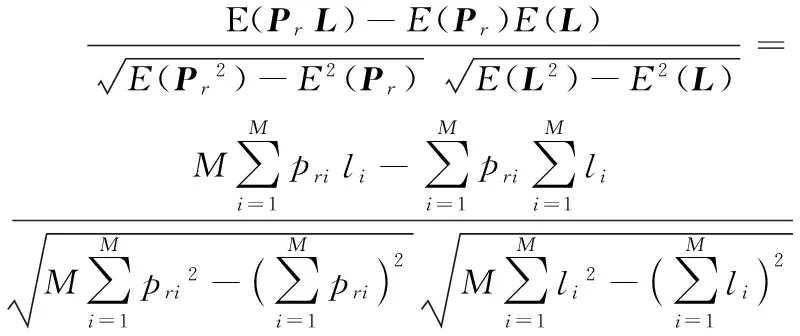
2.4 PCC定位算法步骤
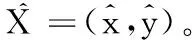
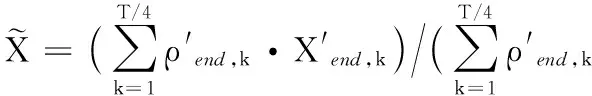
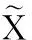
3 仿真及实验分析
3.1 仿真环境
3.2 算法参数的优选仿真分析

3.3 定位算法性能仿真分析
3.4 实际测试实验分析

4 结语

