地空信道下基于OFDM/OQAM系统的时频同步算法

唐亚欣，李燕龙，杨 超，王 波

(1.认知无线电与信息处理省部共建教育部重点实验室(桂林电子科技大学), 广西 桂林 541004;2.中国电子科技集团公司第54研究所 通信网信息传输与分发技术重点实验室, 石家庄 050081)

0 引言

正交频分复用/交错正交幅度调制(Orthogonal Frequency Division Multiplexing/Offset Quadrature Amplitude Modulation, OFDM/OQAM)技术通过采用具有良好的时频聚焦特性的脉冲成型滤波器，能够在不降低系统传输效率的情况下有效抵抗码间串扰(Inter-Symbol Interference, ISI)和子载波干扰(Inter-Carrier Interference, ICI)[1]，但是OFDM/OQAM系统由于没有添加循环前缀(Cyclic Prefix, CP)，一旦出现时间误差，快速傅氏变换(Fast Fourier Transformation, FFT)窗口就会错位造成OFDM/OQAM块间干扰，若出现较大频偏则会破坏子载波间正交性而影响系统的正确解调，因此一个良好的同步算法对于OFDM/OQAM系统的正确解调尤其重要。

目前关于OFDM/OQAM系统中同步算法按原理可以分为两种。

第一种是非数据辅助类(Non data-aided)盲估计算法:文献[2]中首次提出利用接收信号的非共轭循环平稳特性完成时频偏盲联合估计算法；文献[3]在低信噪比情况下，基于最大似然准则通过利用数据经过成型滤波之后的共轭和非共轭相关函数来进行载波频率偏移(Carrier Frequency Offset, CFO)估计；文献[4]利用近似共轭对称特性在OFDM/OQAM信号开始时进行时频联合估计。盲估计算法由于没有导频开销而节约一定量时频资源，但是随着系统对估计精度要求的提高，其观察时长和捕获时间相对较长，复杂度较高，因此并不适用于对实时性要求高的实际应用中。

另外一种OFDM/OQAM系统的同步算法是数据辅助类(Data-aided)时频同步算法，数据辅助虽会降低一定的频谱利用率，但实用性较强。文献[5]提出了一种基于近似最大似然(Approximate Maximum Likelihood, AML)估计准则的时频联合算法，适用于多普勒频移较小的信道状态；文献[6]在最小二乘(Linear Square, LS)估计的基础上，提出一种基于数据辅助的改进最小二乘(Modified Linear Square, MLS)算法；利用相同的导频结构，文献[7]在OFDM/OQAM系统中提出时频联合同步的训练序列(TRaining sequence 1 & TRaining sequence 2, TR1 & TR2)算法，文献[8]对TR2算法进行改进，添加了滑动窗，文献[9]基于最大后验概率进行时频偏估计使符号定时更准确；文献[10]提出利用 Zadoff和Chu提出的ZC序列作数据导频进行频偏估计。但以上算法均只适用于加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道和较小多普勒频移下的慢速衰落多径信道。

针对上述问题，本文基于大多普勒频移快时变的地空信道提出了一种新的自相关估计(AutoCorrelation Estimation, ACE)时频同步算法，通过在时域插入较少的辅助序列可以快速准确地进行符号定时，接收时采用自相关函数结合加权平均的思想进行频偏估计，以较小的计算复杂度为代价，在地空信道下获得了良好的系统误码性能。

1 系统模型

一个典型的OFDM/OQAM系统的连续时间发送信号可以由式(1)[11]所示：

(1)

其中：M表示子载波的个数；am,n表示OFDM/OQAM中第m个子载波、第n个符号上的实值数据符号；gm,n(t)表示时频格点坐标为(m,n)处的基函数；g(t)为良好的时频聚焦特性的IOTA(Isotropic Orthogonal Transform Algorithm)滤波器函数；ν0和τ0分别表示子载波间隔与相邻的实部数据与虚部数据之间的时域偏移，且τ0ν0=1/2。

由文献[12]可知，地空信道是由一条直射路径(Line of Sight, LOS)和其他非直射路径(Non-Line Of Sight, NLOS)叠加而成的，非直射路径为多个散射波分量，其时变脉冲响应一般采用广义平稳非相关散射(Wide Sense Stationary Uncorrelated Scattering, WSSUS)函数表示[12]，地空信道模型由式(2)[12]表示：

h(τ,t)=hLOS(t)+hNLOS(τ,t)=a·ej2πfDLOSt+

(2)

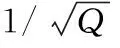
将地空信道的幅度系数简化可以表示为式(3)：

(3)

经过地空信道后，接收到的数据可以表示为式(4)：

r(t)=s(t)⊗h(τ,t)=a·ej2πfDLOSts(t)+

(4)

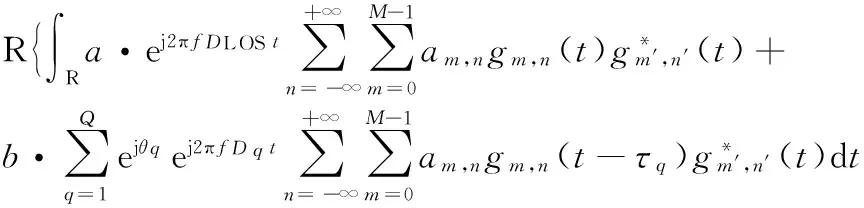
(5)

其中R{·}为取实操作，将上式化简整理得式(6)：

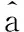
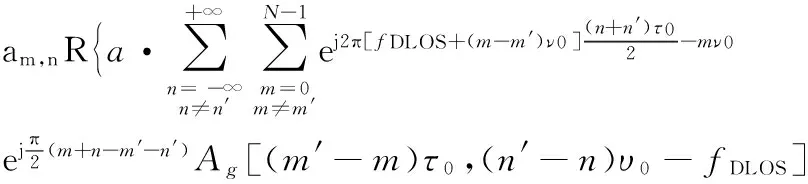
(6)

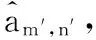
2 ACE时频同步算法

地空信道下基于OFDM/OQAM系统的ACE时频同步算法的结构可由图1表示。

ACE同步算法用于OFDM/OQAM系统中的收发结构如图1所示，包括正交振幅调制(Quadrature Amplitude Modulation, QAM)、误比特率(Bit Error Rate, BER)、信源产生模块、频域导频设计模块、OQAM调制模块、FFT、快速傅里叶反变换(Inverse Fast Fourier Transform , IFFT)、时域辅助序列、地空信道模块、ACE同步算法模块、OQAM解调模块和误码率比较模块。下面就导频设计和同步算法本身从数学角度进行阐述。

图1 ACE同步算法的OFDM/OQAM系统结构框图 Fig. 1 Block diagram of OFDM/OQAM system for ACE synchronization algorithm

2.1 频域导频设计

目前，基于数据辅助的方法进行OFDM/OQAM系统的时频同步较常见的是在发送端插入一定数量的导频序列。文献[6-9]中提出的时频同步方法给出了其相应的导频构造，其原理是在频域添加NTR个重复的OFDM频域符号构成相应的导频块，如式(7)所示：

(7)

发送时域信号如式(8)所示：

(8)

将式(1)代入式(9)得：

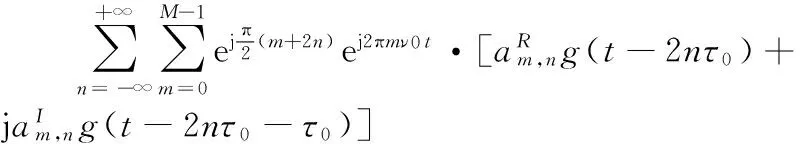
(9)

假设脉冲成型滤波器函数g(t)在t∈{0,Ts,…,(Ng-1)Ts}内非零，Ng=K·T/Ts，其中K表示滤波器的重叠因子(即抽头系数)，T=M·Ts为符号时间，Ts为采样间隔。在本文中，添加的导频训练序列可以表示为sTR(t)，对sTR(t)进行采样如式(10)所示：

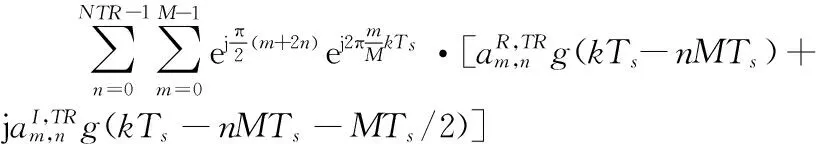
(10)

在传输了Ng+1采样点后，区间k∈{Ng+1,Ng+2，…,NTRM-2M}内的训练序列满足：

sTR(kTs)=-sTR(kTs+MTs)

(11)

sTR(kTs)=sTR(kTs+2MTs)

(12)

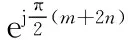
由于加入的相位偏移因子不同，在文献[6]中sTR(kTs)=sTR(kTs+MTs)，而在本文系统中sTR(kTs)=sTR(kTs+2MTs)，因此对传统算法进行重新定义。相关的区间也由k∈{Ng-1,Ng，…,NTRM-M-1}变为k∈{Ng+1,Ng+2，…,NTRM-2M}，本文选取相关区间刚好为一个符号时间T内的采样点数T/Ts，便于时频同步算法的计算与实现。

2.2 ACE算法

OFDM/OQAM系统中，本文按照上节的分析对文献[7]和文献[6]中的TR2和MLS算法进行重新建模如下。

TR2时频同步算法[7]：

(13)

(14)

其中：

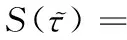
(15)

(16)

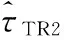
MLS时频同步算法[6]：

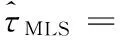
(17)

(18)

(19)

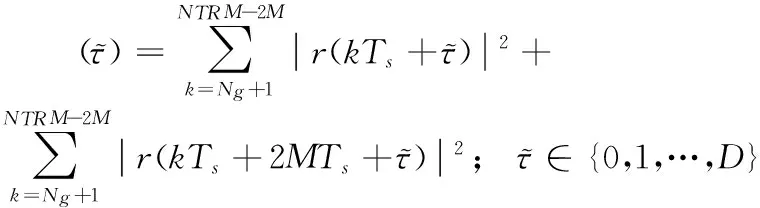
(20)

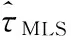
经过详细对比上述两种传统算法的符号定时性能可以发现，采用基带接收信号的帧序列r(kTs)和发送基准序列s(kTs)进行互相关运算的TR2算法优于利用基带接收信号r(kTs)和r(kTs+2MTs)进行自相关运算的MLS算法。但可以看出TR2和MLS算法符号定时选取的相关序列较长，耗时较久，比较适用于普通的AWGN信道或慢速衰落的多径信道。

同时比较两种传统算法的频偏估计性能可以发现，由于在系统中基带接收信号r(kTs)和r(kTs+2MTs)经历了相似的信道环境，所以TR2和MLS算法的频偏估计精度相同。

本文结合地空信道的特点对传统时频同步算法进行改进提出了ACE算法，其基本思想是将符号定时和频偏估计分为两部分进行。如图1所示：符号定时利用10 b的辅助序列来进行符号定时，既提升了符号定时精度又大大缩短了定时时间；频偏估计在传统估计算法只进行一次相关操作的基础上进行改进，在接收端进行两次相关运算，将两次计算估计的频偏值进行加权平均。

在图1发送数据过信道前加入Na=10 b的OFDM符号作为训练序列z(kTs)，经过信道后得到z′(kTs)。

(21)

其中：

(22)

(23)

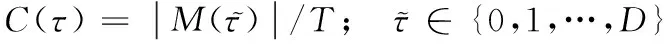
(24)

图1中频域导频设计模型：根据文献[6]在传统算法中NTR至少要比滤波器重叠因子K大2，但ACE算法原理是在接收端得到两对相等的序列做两组相关运算，因此在本文中取NTR=K+3。本文频域导频设计模型已在2.1节介绍，此处不作赘述。

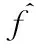
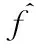
(25)

(26)

(27)

其中：

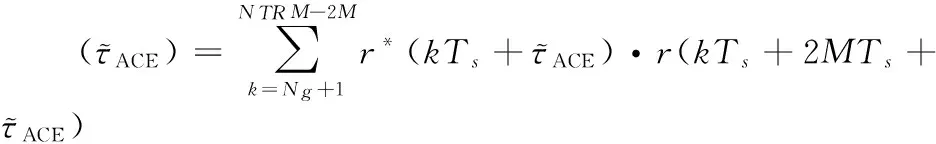
(28)

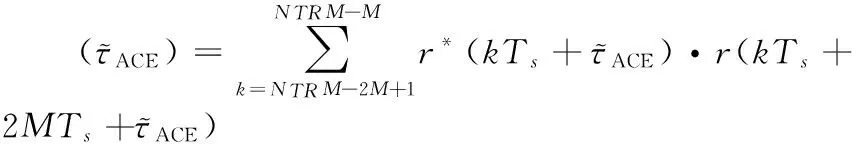
(29)

由式(21)～(29)可分析得出：ACE算法符号定时中，虽插入了10 b的时域导频序列，但10 b远远小于帧的长度，对系统传输效率造成的影响可忽略不计。频偏估计中虽然表面上增加了一次相关操作，但相关区间为固定值不用再进行滑动选取从而降低了运算复杂度；并且ACE算法的相关运算从原有的2个导频序列增加到4个导频序列，提高了导频利用率，更大范围地获取信道状态信息，更适用于具有大多普勒频移的快时变地空信道。

3 仿真结果分析

将本文提出的ACE算法与传统TR2和MLS算法在地空信道下进行仿真比较。地空信道的信道状态包括停场、滑行、飞行和到达四种状态，每种信道状态的具体参数设置如表1所示[12]。

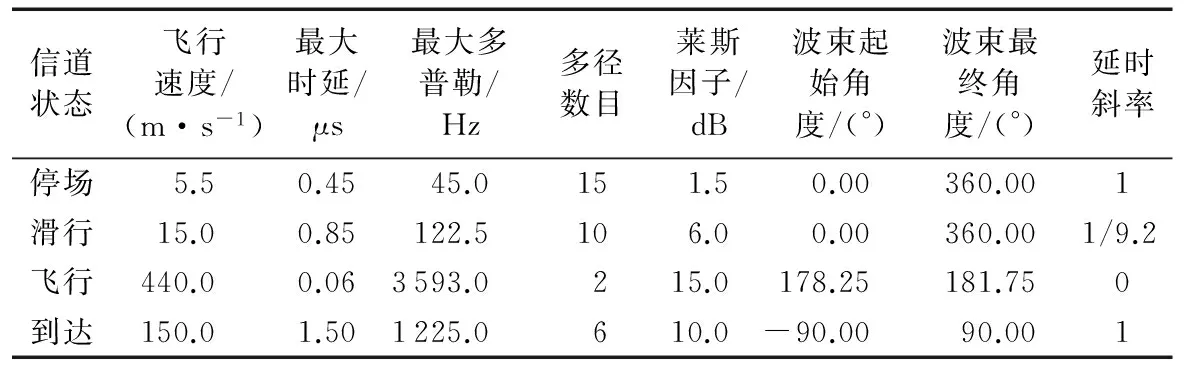
表1 地空信道参数设置Tab. 1 Ground-air channel parameter setting

从表1中可以看出，地空信道中的停场和滑行状态下信道变化较慢，多普勒频移也较小，OFDM/OQAM系统本身对多普勒频偏具有一定的容忍度，因此本文仅仿真分析飞行和到达状态下的同步算法性能结果。

OFDM/OQAM系统仿真相关参数如表2所示。

表1根据文献[12]列出的典型地空信道参数作为本文地空信道的参数设置；表2根据文献[13]中802.11n第四代无线通信标准相关参数设定，中心频率设为2.4 GHz，带宽设为20 MHz，编码类型定为OFDM/OQAM，分别选用4QAM和16QAM两种较为典型的调制技术作为本文仿真参数。

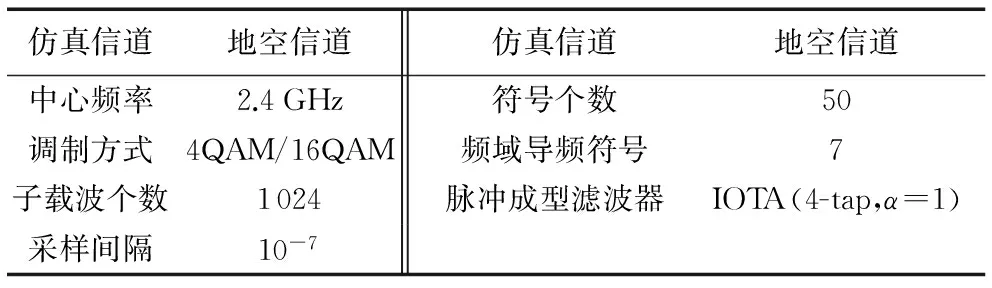
表2 OFDM/OQAM系统仿真参数设置Tab. 2 OFDM/OQAM system simulation parameter setting

图2根据式(24)中的定义的成本函数C(τ)，比较了在地空信道下本文提出的ACE算法和TR2、MLS两种传统同步算法的时偏估计性能。可以看出，在地空信道下ACE算法相关峰的旁瓣峰值均为0.1左右，而TR2算法旁瓣峰值均在0.3左右，本文提出的ACE算法相关峰值对比度与TR2和MLS算法对比，提高至原来的3倍，对比度越高时偏估计结果越精确；ACE算法只采用10 b的辅助序列进行时偏估计，辅助数据越短，受信道的影响越小，其相关结果越精确，同时计算复杂度远远低于TR2算法，更易于工程实现。

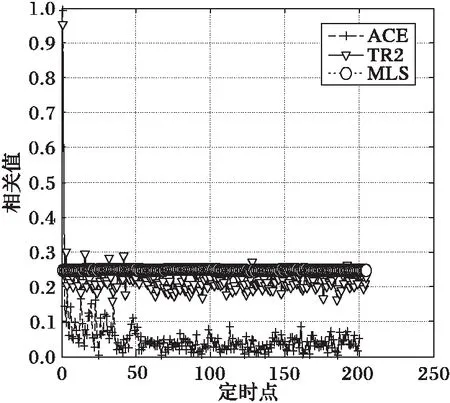
图2 时偏估计相关函数 Fig. 2 Time offset estimation correlation function

图3表示地空信道飞行状态下OFDM/OQAM系统不同同步算法频偏估计的均方根误差(Root Mean Squared Error, RMSE)性能比较。从仿真结果可以看出：地空信道中以环境最差的飞行状态为例，在均方根误差为稍大于10-2时，本文所提出的ACE时频同步算法相对于传统TR2和MLS同步算法分别有6 dB和11 dB的性能优势，在高信噪比下，性能优势更加明显。

图4和图5分别表示地空信道飞行状态和到达状态下不同同步算法4QAM和16QAM时系统的误码率(BER)性能比较。从仿真结果可以看出：地空信道的飞行和到达状态下，本文所提出的ACE时频同步算法的OFDM/OQAM系统误码率均低于传统同步算法；相比TR2和MLS算法，地空信道中多普勒频偏越大，ACE同步算法的BER性能越好。飞行状态下，在BER=10-2时，ACE算法相比TR2和MLS算法有10 dB的信噪比增益；到达状态下，在BER=10-3时，ACE算法相比TR2和MLS算法有3 dB的信噪比增益。

4 结语

本文针对OFDM/OQAM系统在地空信道下的时频同步问题，提出一种ACE算法。该算法利用较短的时域导频序列进行符号定时，相关序列长度大幅减少，从而缩短符号定时时间，更易于工程实现。其次，ACE同步算法在传统频偏估计算法的基础上提出了一种改进的加权平均频偏估计方法，更适用于快速衰落且存在较大多普勒频移的地空信道，从而提高了频偏估计的准确性。仿真结果表明，ACE同步算法相比传统的同步算法在增加较小复杂度的情况下进一步减小了均方根误差，从而提高OFDM/OQAM系统在地空信道下的误码性能。

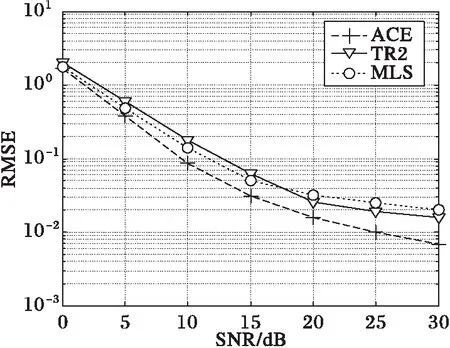
图3 飞行状态下系统RMSE曲线 Fig. 3 System RMSE curve at en-route state

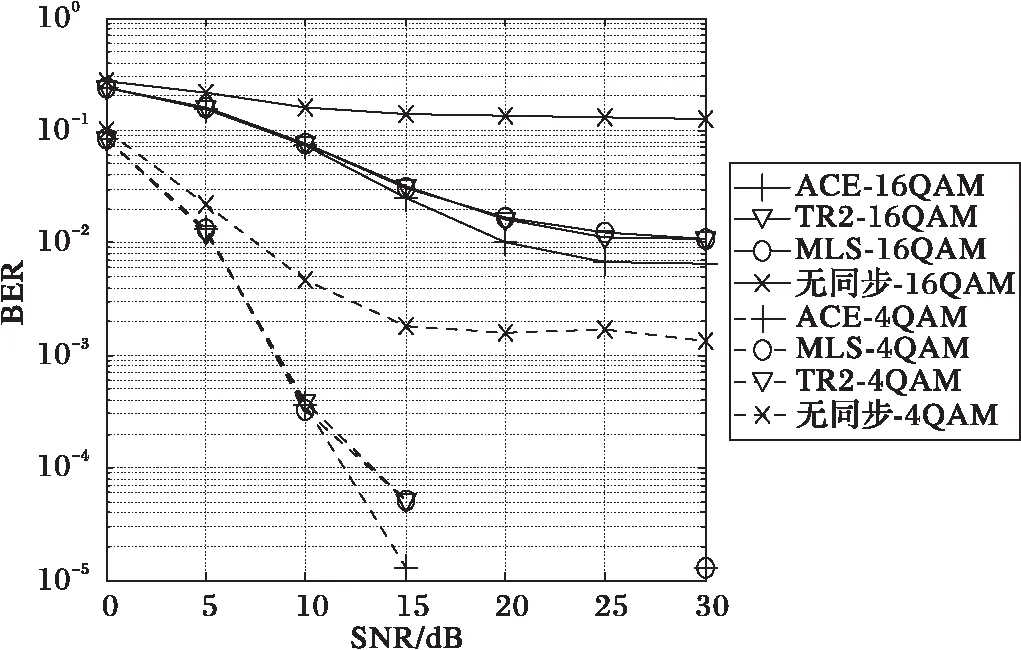
图4 飞行状态下系统BER性能比较 Fig. 4 System BER performance comparison at en-route state

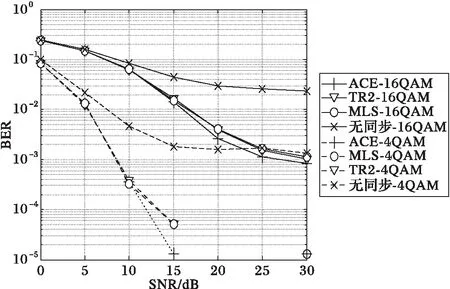
图5 到达状态下系统BER性能比较 Fig. 5 System BER performance comparison at arrival state

参考文献(References)

[1] 程国兵.OFDM/OQAM系统中的关键技术研究[D].成都：电子科技大学,2013:59-63.(CHENG G B. Research on key technology in OFDM/OQAM system [D]. Chengdu: University of Electronic Science and Technology, 2013:59-63.)

[2] BOLCSKEI H. Blind estimation of symbol timing and carrier frequency offset in pulse shaping OFDM systems [J]. IEEE Transactions on Communications, 2001, 49(6):988-999.

[3] FUSCO T, PETRELLA A, TANDA M. Non-data-aided blind carrier-frequency offset estimation for pulse shaping OFDM/OQAM systems [J]. Signal Processing, 2008, 88(8): 1958-1970.

[4] MATTERA D, TANDA M. Blind symbol timing and CFO estimation for OFDM/OQAM systems [J]. IEEE Transactions on Wireless Communications, 2013, 12(1): 268-277.

[5] FUSCO T, PETRELLA A, TANDA M. Joint symbol timing and CFO estimation for OFDM/OQAM systems in multipath channels [J]. EURASIP Journal on Advances in Signal Processing, 2010, 2010: Article No. 3.

[6] FUSCO T, PETRELLA A, TANDA M. Data-aided symbol timing and CFO synchronization for filter bank multicarrier systems [J]. IEEE Transactions on Wireless Communications, 2009, 8(5): 2705-2715.

[7] FUSCO T, PETRELLA A, TANDA M. Data-aided time-domain synchronization for filter bank multicarrier systems [EB/OL]. [2017- 03- 04]. http://www.eurasip.org/Proceedings/Eusipco/Eusipco2008/papers/1569101898.pdf.

[8] TONELLO A M, ROSSI F. Synchronization and channel estimation for filtered multitone modulation [EB/OL]. [2017- 03- 04]. http://www.diegm.uniud.it/tonello/PAPERS/CONFERENCES/WPMC2004_1.pdf.

[9] YANG G, CHEN H, HU S, et al. Data-aided joint symbol timing and CFO estimation for OFDM/OQAM systems [C]// ICCSP 2011: Proceedings of the 2011 International Conference on Communications and Signal Processing. Piscataway, NJ: IEEE, 2011: 1-5.

[10] CHEN H, HU S, WU G, et al. A data-aided OFDM/OQAM synchronization algorithm using maximum posterior probability criterion [C]// IET ICCTA 2011: Proceedings of the 2011 Institution of Engineering and Technology International Conference on Communication Technology and Application. Stevenage, UK: IET, 2012:107-111.

[11] WANG J, DU X, HE Z, et al. A novel data-aided joint timing and carrier frequency offset estimation based on central symmetry ZC sequence in OFDM/OQAM systems [J]. Wireless Personal Communications, 2016, 90(4): 1619-1634.

[12] HAAS E. Aeronautical channel modeling [J]. IEEE Transactions on Vehicular Technology, 2002, 51(2): 254-264.

[13] 郭政.5G WiFi标准——802.11ac解析及应用展望[J].科技传播,2012,4(15):187-188.(GUO Z. 5G WiFi standard — the 802.11ac analytical and application prospects [J]. Public Communication of Science & Technology, 2012, 4(15): 187-188.)

This work is partially supported by the National Natural Science Foundation of China (61371107), the Guangxi Wireless Broadband Communication and Signal Processing Key Laboratory Fund (GXKL061501), the Cognitive Radio and Information Processing, Key Laboratory of the Ministry of Education, 2016 Director Fund Funding Project (LD16112X), the Cognitive Radio and Information Processing, Key Laboratory of the Ministry of Education, 2015 Director Fund Funding Project (CRKL150111).

TANGYaxin, born in 1993, M. S. candidate. Her research interests include broadband wireless communication.

LIYanlong, born in 1989, Ph. D. candidate, lecturer. His research interests include mobile communication.

YANGChao, born in 1988, Ph. D. candidate. His research interests include broadband signal processing.

WANGBo, born in 1977, Ph. D., lecturer. His research interests include wireless communication.