基于扩展卡尔曼滤波的三维风速在线估计方法

涂海峰 贾生伟 阳丰俊 吕 瑞

中国运载火箭技术研究院，北京100076

风作为飞行器的重要外部环境因素，对飞行器的飞行起着至关重要的作用，尤其是小型飞行器，如小型无人机、四旋翼等，很容易受到风的影响[1-3]。风具有较强的随机性，很难通过建模的方式计算地球任何一点的风速信息[4]，工程上通常采用机载设备的测量数据实现风速的估算。在国内外已经有学者展开通过飞行器有限的飞行数据对风场进行估计的研究。在国外，Brezoescu等[2]采用运动方程计算得到的飞行数据与传感器的测量数据的差估计风速，同时提出用在线自适应技术处理传感器噪声。Jack等[5]研究采用GPS/INS、空速等测量数据实现小型或微型飞行器周围的风速和风速梯度的估计。LEFAS等[6]采用空速和雷达测量数据实现了风速的估计，Harish等[7]采用飞行数据通过无迹卡尔曼滤波实现了有航向角和无航向角观测数据情况下的风速估计。在国内，刘林[8]通过风速、空速、地速的三角关系构建了风场估计模型，并通过卡尔曼滤波实现风场的估计。屈耀红[4]在其博士论文中根据风速的矢量关系提出了多步长法，并采用卡尔曼滤波器实现风场的估计。周伟静等[9]采用粒子滤波算法实现对一阶时变自回归风速模型的估计。这些学者进行风速估计时采用空速管的数据近似为飞行器的真实空速，忽略了攻角和侧滑角的影响。

Cho等[10]利用GPS和空速管测量数据估算水平面内的风向和风速，在建立风速估计模型时考虑到了攻角和侧滑角的影响，并通过飞行试验进行了验证。何波等[11]也采用类似方法进行风速和风向的估计。他们仅实现了水平风场信息的估计，没有对铅垂面内的风进行建模和估计，而对于在对流层内飞行的巡飞弹药来说，铅垂面内的风也需要考虑。

在线估计风向和风速通常建立状态空间模型，通过卡尔曼滤波实现，然而能否在飞行中估计出精确结果，取决于系统是否可观测。对系统可观测性的分析已经有较多的研究，钱伟行、刘建业等[12]运用谱条件数方法分析了载体在转动基座初始对准系统中各状态量的可观测度；高伟熙等[13]将陀螺角速度误差作为观测量引入静基座对准系统，通过可观测性的定性分析和可观测度的定量计算后发现可提高系统的可观测度；游金川、秦永元等[14]利用分段定常系统可观测性分析方法分析了加速度计的尺寸效应估计系统状态的可观测性；乔国栋等[15]基于能观度分析，提出了一种地月转移轨道的自主导航算法。

考虑巡飞弹由于空间和成本的限制，无法安装攻角和侧滑角传感器，因此采用弹载的GPS/MIMU组合导航系统的输出数据与空速管测量的动压值，通过扩展卡尔曼滤波实现地面坐标系下三维风速的在线估计，并利用数值仿真试验进行验证。

1 风速估计原理

在地面坐标系中，巡飞弹药相对于地面的速度矢量Vg，相对于空气的速度矢量Va以及空气相对于地面的速度矢量Vwg构成三角关系[8](见图1)，则有：

Vg=Va+Vwg

(1)

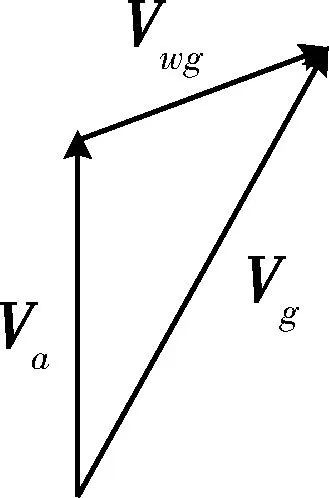
图1 风速的三角关系图

其中，Vg可以通过巡飞弹药中的GPS/MIMU组合导航系统计算得到，空速可通过图2所示的方式转换到地面坐标系中，其计算公式为：

(2)

式中，L(ψ,θ,φ)为弹体系到地面系的转换矩阵，L(-α,β)T为速度坐标系到弹体坐标系的转换矩阵，Va为速度坐标系下的空速值。

图2 空速的分解图

本文所研究的巡飞弹药中并未安装用于测量攻角和侧滑角的传感器，只在轴向上安装了空速管用于测量轴向上的动压值，可算得巡飞弹药纵向轴的空速，不能得到攻角和侧滑角信息。因此，不能通过式(2) 的实时计算得到空速在地面坐标系中的分量，进而计算出风场信息。然而空速管计算得到的轴向空速可用于空速大小的估算。空速在机体坐标系下的投影为：

(3)

式中，Vab为空速在弹体坐标系下的矢量。因此空速管测得的空速Vpitot与真实空速的关系如下：

(4)

巡飞弹药中的空速管可以测量动压，根据伯努利方程，其空速测量原理为[10-11]：

(5)

式中，ΔP表示动压，ρ为空气密度，K为校正因子，用于校正由温度、空气黏度、不稳定气流以及安装误差等引起的空速管测量误差。式(4)代入式(5)可得：

(6)

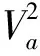
2 基于EKF的三维风速在线估计方法

空速管在测量风速时会存在较大的高频噪声[8]，为了获得平滑、精度较高的风速估计值，采用EKF实现风速的非线性估计。式(6)可作为风速估计的量测方程，因此还需建立风速估计的状态方程。风的模型有很多种，如定常风、突风(阵风)、风切变和湍流等。为了不失一般性，本文只关注定常风。风速在地面坐标系中的分解如图3所示。

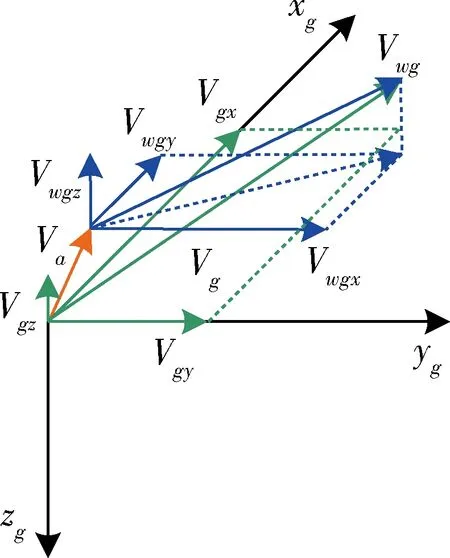
图3 空速和地速在地面坐标系中的分解图

需要估计得到的状态量为：

(7)

本文主要针对常值风进行估计，其在空中缓慢变化，因此根据离散化状态转移模型，加入白噪声便可建立系统的状态方程[11]，如式(8)所示：

x(k+1)=Fx(k)+wk

(8)

式中，

(9)

其中，k表示第k次迭代值。系统方程已经得到，下面还需要对量测方程进行适当的变形。根据风速的三角形关系，可有：

(10)

式中，Vgx，Vgy和Vgz可由GPS/MIMU组合导航系统输出，ΔP可由空速管实时测量得到，可以作为系统的量测信息，因此可由式(10)得到系统的量测方程为：

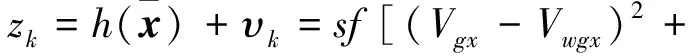
(11)

其中，υk∈N(0,R)为量测白噪声。该量测方程为非线性方程，需要求取其Jacobian矩阵得到线性观测矩阵为：

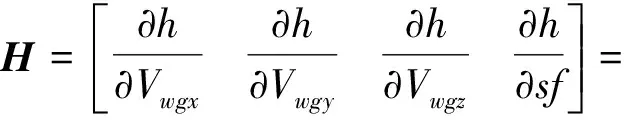
(12)

线性化的状态方程和观测方程都已经求得，便可以用EKF进行迭代求解得到风速的估计值。

该方法要实现风速值的估计，还需要满足可观测性的要求，即需要满足状态量完全可观测。系统的可观测性可通过求取可观测矩阵的秩，如果为满秩矩阵则完全可观测，不满足则不完全可观测[18]。

根据式(8)和(12)建立可观测矩阵为：

(13)

矩阵F为单位矩阵，则上式可变为：

(14)

显然可观测矩阵的秩rank(O)=4，观测矩阵为满秩矩阵，因此系统完全可以观测，即通过扩展卡尔曼滤波实现风速的估计是可行的。

在进行滤波估计之前，还需要确定滤波的初始值，以便于卡尔曼滤波能快速收敛。根据风速的三角形公式，可通过滤波初始时刻的巡飞弹药的初始地速和空速管测量的空速通过下式计算得到近似的风速值。

(15)

其中，下标“0”表示初始时刻。过程噪声需要根据天气情况进行设定，而量测噪声可以通过实验测得。在实际应用中，虽然可观测矩阵为满秩，还需有足够的激励信息才能实现风速的估计。对三维风速信息的估算，既需要通过水平方向的机动使得测量数据中包含足够的信息以实现水平方向常值风速的准确估计，还需要在铅垂方向进行必要的机动实现纵向风速的估计。

3 风速估计的数值仿真试验验证

使用巡飞弹药仿真平台，在仿真中加入常值风的干扰。为实现三维风速的估计，设定如图4(a)中的1-4点为航路点，并将其中1和3的目标飞行高度设置为700m，2和4点的目标高度设置为600m，飞行中每隔300s变换一次三向风速。仿真飞行的平面轨迹如图4(a)所示，三维轨迹如图4(b)所示。

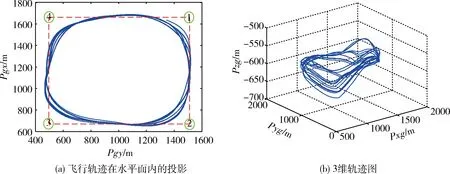
图4 飞行轨迹图

仿真中用到的状态初值由式(15)确定，其他初值设定如下：

(16)

三维风速的估计结果如图5所示，三维风速的估计值与真值的误差如图6所示。可以看出，在300s内，所提算法能准确地估计出三向的风速值和比例因子。估计稳定之后三向风速的估计结果如表1所示，水平风速误差不大于0.1m/s，垂直方向的风速误差不超过0.4m/s，估计精度较高。

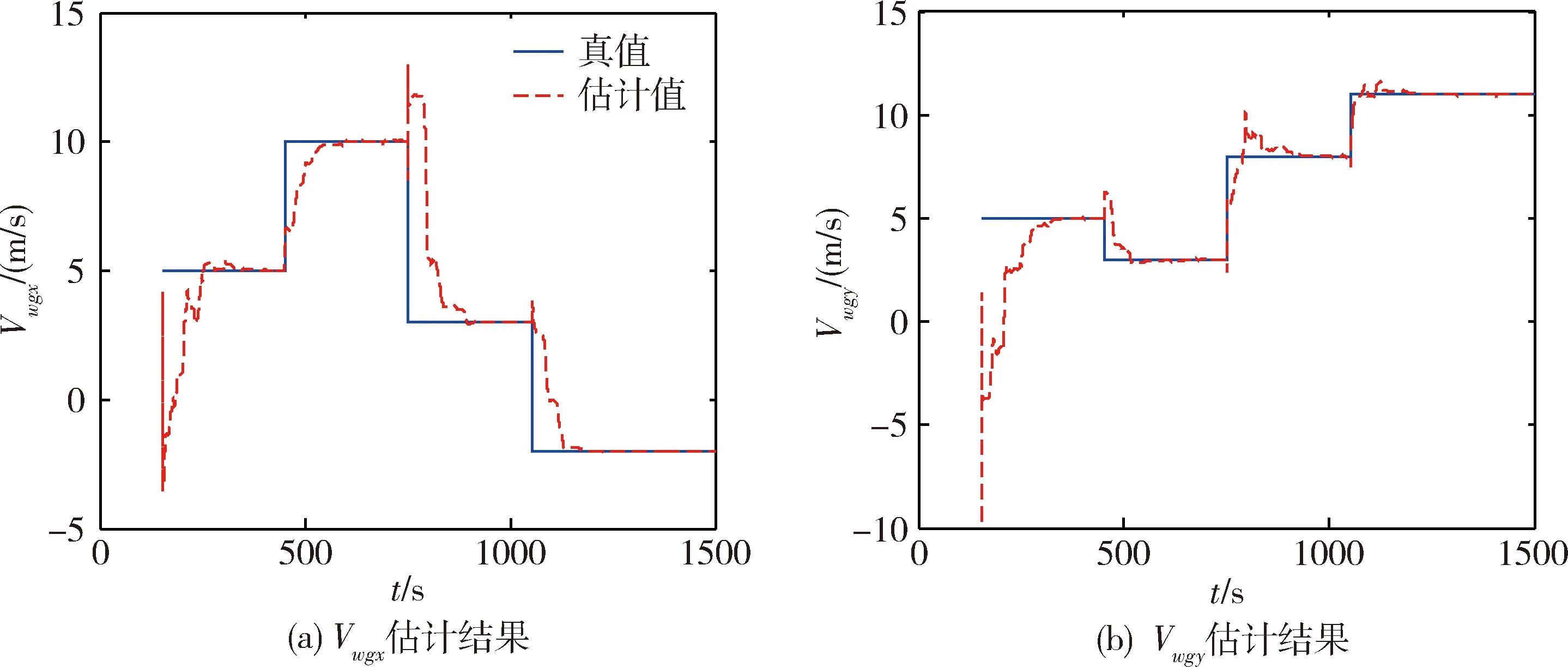
图5 滤波估计结果与真值的对比

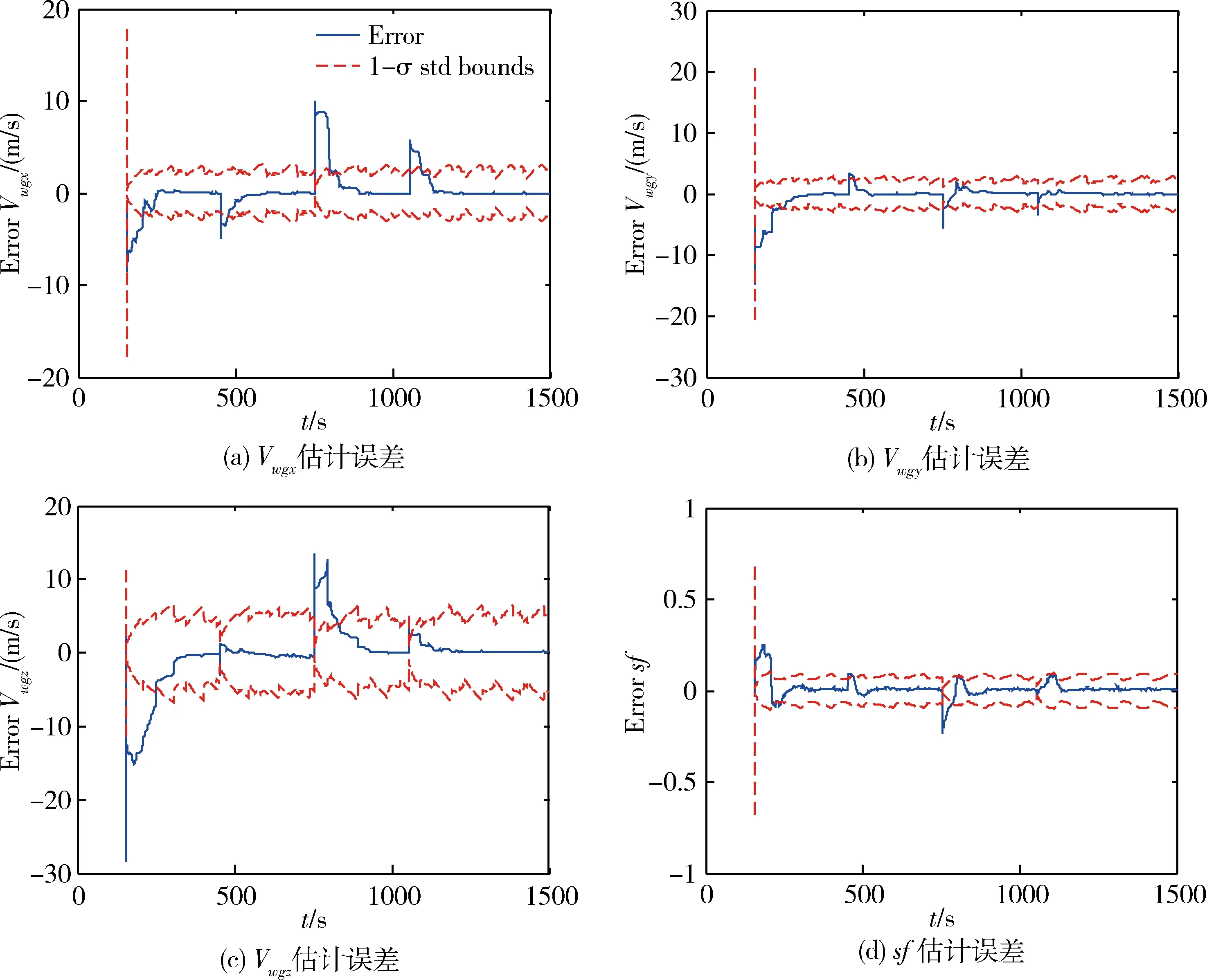
图6 滤波结果与真值的误差

风场变化次数Vwgx真值Vwgx估计值Vwgy真值Vwgy估计值Vwgz真值Vwgz估计值155．04354．98421．88521010．0432．95954．631332．99688．09511．1124-2-2．0091110．991-2-1．828

4 结论

由于成本和空间的限制，本文研究的巡飞弹药没有安装测量攻角和侧滑角传感器，只能通过估算得到。然而在有风的情况下，攻角和侧滑角的估算精度低。因此通过构建风速估计模型，采用扩展卡尔曼滤波算法，利用巡飞弹药中的GPS/MIMU和空速管的输出在线估计出风速信息。仿真试验表明：当滤波收敛后，水平风速精度小于0.1m/s，铅垂方向风速精度小于0.4m/s。

参 考 文 献

[1] 高社生, 张极, 党进伟. 风场估计算法及其在组合导航中的应用[J]. 飞行力学, 2013, 31(5):467-471. (Gao Shesheng, Zhang Ji, Dang Jinwei. Wind Field Estimation Algorithm and Its Application in Integrated Navigation[J]. Flight Dynamics, 2013, 31(5):467-471.)

[2] Brezoescu A, Castillo P, Lozano R. Wind Estimation for Accurate Airplane Path Following Applications[J]. Journal Intelligent and Robotic Systems, 2014, 73(4): 823-831.

[3] Morelli E A. Real-Time Aerodynamic Parameter Estimation without Air Flow Angle Measurements[J]. Journal of Aircraft, 2012, 49(4): 1064-1074.

[4] 屈耀红. 小型无人机航迹规划及组合导航关键技术研究[D]. 西安: 西北工业大学, 2006.(Qu Yaohong. Study on the Key Techniques of Trajectory Planning and Integrated Navigation of UAV[D]. Xi’an，Northwestern Polytechnical University, 2006.)

[5] Langelaan J W, Alley N, Neidhoefer J. Wind Field Estimation for Small Unmanned Aerial Vehicles[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(4): 1016-1030.

[6] Lefas C C. Real-Time Wind Estimation and Tracking with Transponder Downlinked Airspeed and Heading Data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, 23(2): 169-174.

[7] Palanthandalam-Madapusi H J, Girard A, Bernstein D S. Wind-Field Reconstruction Using Flight Data[C]. 2008 American Control Conference. Washington, USA, 2008.

[8] 刘林. 在飞行中进行风场估计[J]. 飞行力学, 1992, 10(3): 41-48.(Liu Lin. Wind Estimation in Flight[J]. Flight Dynamics, 1992, 10(3): 41-48.)

[9] 周伟静, 达兴亚, 沈怀荣. 基于粒子滤波算法的风场估计方法[J]. 系统仿真学报, 2009, 21(2): 38-42.(Zhou Weijing, Da Xingya, Shen Huairong. Research of Wind Estimation Based on Particle Filter[J]. Journal of System Simulation, 2009, 21(2): 38-42.)

[10] Cho A, Kim J, Lee S, et al. Wind Estimation and Airspeed Calibration Using a UAV with a Single-Antenna GPS Receiver and Pitot Tube[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 109-117.

[11] 何波, 李荣冰, 刘建业等. 基于扩展卡尔曼滤波的风速估计算法研究[J]. 电子测量技术, 2014, 37(6): 34-37.(He Bo, Li Rongbing, Liu Jianye, et al. Estimation Algorithm for Airborne Wind Based on Extended Kalman Filter [J]. Electronic Measurement Technology, 2014, 37(6): 34-37.)

[12] 钱伟行, 刘建业, 赵伟, 赵文芳. 基于转动基座的SINS初始对准方法研究[J]. 宇航学报, 2008, 29(3): 928-932.(Qian Weihang, Liu Jianye, Zhao Wei, Zhao Wenfang. SINS Initial Alignment Based on Revolving Base [J]. Journal of Astronautic, 2008, 29(3): 928-932.)

[13] 高伟熙, 缪玲娟, 倪茂林. 一种引入陀螺角速度信息的快速对准方法[J]. 宇航学报, 2010, 31(6): 1596-1601.(Gao Weixi, Miao Lingjuan, Ni Maolin. A Fast Initial Alignment Method with Gyro Angular Rate Information[J]. Journal of Astronautic, 2010, 31(6): 1596-1601.)

[14] 游金川, 秦永元, 杨鹏翔, 严恭敏. 捷联惯导加速度计尺寸效应误差建模及标定[J]. 宇航学报, 2012, 33(3): 311-317.(You Jinchuan, Qin Yongyuan, Yang Pengxiang, Yan Gongmin. Modeling and Calibration of the Accelerometer Size Effect Error of the SINS[J]. Journal of Astronautic, 2012, 33(3): 311-317.)

[15] 乔国栋, 倪茂林, 李铁寿. 基于能观度分析的信息融合自主导航算法[J]. 宇航学报, 2008, 29(3): 883-888.(Qiao Guodong, Ni Maolin, Li Tieshou. Observability-Based Information Fusion Autonomous Navigation Algorithm[J]. Journal of Astronautic, 2008, 29(3): 883-888.)

[16] Rhudy M, Larrabee T, Chao H, et al. UAV Attitude, Heading, and Wind Estimation Using GPS/INS and Air Data System[C]. AIAA Guidance, Navigation, and Control Conference. Boston, MA, 2013.

[17] Petrich J, Subbarao K. On-Board Wind Speed Estimation for UAVs[C]. AIAA Guidance, Navigation, and Control Conference. Portland, Oregon, 2011.

[18] 杨晓霞, 阴玉梅. 可观测度的探讨及其在捷联惯导系统可观测性分析中的应用[J]. 中国惯性技术学报, 2012, 20(4): 405-409.(Yang Xiaoxia, Yin Yumei. Discussions on Observability and Its Applications in SINS[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 405-409.)