篮下侧旋打板投篮的动力学分析

杨大有

(郑州市第一中学 河南 郑州 450052)

1 问题的提出

篮球对抗赛中，篮下区域投篮，球空中行程短，命中率高于中长距离投篮，历来是攻防最激烈的地方，也是篮球运动最具魅力之处．由于在篮下防守的严密，进攻队员很难找到恰当的瞄准点直接完成投篮动作, 更多的情况则是借助打板完成投篮，但比赛中又很难在篮下找到合适的打板点．欣赏过NBA骑士队巨星凯里·欧文的比赛后，种种困惑就迎刃而解，他经常能在严密的贴身防守下，不可思议地完成篮球侧旋打板进筐，突破了人们对投篮打板点选择的常规性认识，改变了人们对篮下进球的惯性思维，使“意想不到”成为篮球运动出奇制胜的“法宝”．凯里·欧文精湛的技艺引得无数球迷争相模仿，若要在篮球比赛中完成凯里·欧文式的动作应该把握好哪些要素？这些因素又是如何影响篮球命中率的呢？我们是否能像凯里·欧文一样完成侧旋打板进筐的精彩动作呢？

2 侧旋转球的引入

通过反复观看凯里·欧文的多场篮球比赛视频，发现篮球出手后的侧旋转角速度、平动速度、打板的方向和角度、打板点的位置等因素直接影响到能否进球．凯里·欧文的篮下侧旋转打板上篮，篮球出手时运动的方向与篮板面的竖直夹角很小，基本上是竖直向上，篮球的侧旋转程度越高，其反弹后改变入筐角度越大，在看似不可能打板进筐的“死”角位置也能进球，达到了投篮“出其不意”的命中效果．篮球左旋在高、中、低三个不同位置打板示意图，如图1所示．

图1 篮球左旋在高中低三个不同位置打板

3 动力学分析

3.1 打板时的受力分析

(1)篮板作用在篮球上的摩擦力f．假设篮球出手时沿着竖直方向(Z轴)向左旋转(从上方向下看为顺时针方向旋转，图2)，篮球具有初始角速度ω1，平动初速度v1，由于篮球打板向左旋转，篮板给蓝球一个与侧旋方向相反的摩擦力(图2)，方向沿着X轴正向，篮球质心在摩擦力的驱动下获得了与侧旋方向相反的瞬间加速度，篮球弹离篮板后获得了一个向左的速度v10x(与X轴同向)，此速度应小于或等于ωr(ω为篮球侧旋转角速度，r为篮球半径)，同时在摩擦力矩的阻碍下，篮球侧旋转的角速度(ω10)减小．表示为

v10x<ω1r

(1)

图2 打板后受力分析

(2)N为篮球打板时篮板作用在篮球上的弹力，垂直于篮板，方向沿Y轴正向．

(3)G是篮球受到的重力mg．

3.2 进筐过程中的受力分析

篮球左旋打板后在摩擦力f作用下，反弹方向向左偏移，v10是篮球打板后的速度，偏移角度θ即入篮角度，是速度v10在XY平面上的分速度v10xy与Y轴的夹角；v10与Z轴的夹角为反弹角α′(本文暂不计算)，如图3所示．

图3 打板后篮球的入篮角度

(2)Magnus(马格努斯)力．根据伯努利定律，如果侧旋运动的篮球在绕着竖直方向以顺时针方向旋转时，如图4所示，两侧的压力差使篮球球体受到Magnus (马格努斯)力的作用，力的方向指向空气流速度较大的一侧，并始终与运动方向垂直．

图4 马格努斯效应

(3)篮球受到的重力mg．

3.3 对Magnus力的作用分析

为了检验Magnus力，在篮球场进行了多次侧旋转上篮测试，篮板最高处距离地面3.9 m，假设投球者身高1.75 m，出手打板的高度1.9 m，篮球空中行进的距离在2 m以内．投球者站在篮下(篮板右侧的正下方)，使篮球顺时针向左侧旋转，同时向上投出打板，经反复多次测试发现，篮球打板前的运动轨迹几乎是直线运动(近似于竖直向上)，肉眼较难观察出运动轨迹的弯曲．打板后可以明显看到篮球向左偏向，运动轨迹是曲线(图1)．打板过程中篮球沿Y轴方向行进的距离短(约0.3 m)、分速度较小，且Magnus力的方向沿X轴反方向，与篮球打板后改变的方向相反．篮球弹离篮板后，沿着与Y轴夹角θ方向运动(图3)，这时该力与v10方向垂直，指向篮板．可以得知，该力在短距离内改变篮球运动轨迹的作用不大，可以忽略．

4 篮球的运动规律

以篮球的打板点为坐标原点，建立直角坐标系(图5和图6) ，其中OZ轴竖直向上，OX轴方向指向篮筐，OY轴垂直于篮板指向读者方向．侧旋球打板反弹后的飞行轨迹是一条曲线．

篮球打板后的速度为v10，此速度在XY平面上分速度为v10xy，沿X，Y，Z方向的分速度分别为v10x，v10y，v10z(图5)．

图5 速度合成矢量图

假设球初始绕OZ轴旋转，忽略空气阻力矩，篮球打板后的运动微分方程可简化为

竖直方向

(2)

水平方向

(3)

对式(2)作变形，有

积分

再积分得

其中c1，c2为积分常数，设t=0时，z=0,v=v10z，c1相当于篮球在Z轴方向的分速度v10z，c2=0．

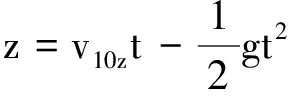
(4)

对式(3)积分

(5)

将t=0,v=v10xy代入式(5)中，得

(6)

考虑到kv10xy与m相比较小，可忽略空气阻力不计，得v=v10xy．

Magnus力忽略不计，θ为入篮角度(图3)．篮球打板后在水平方向内的位移

(7)

(8)

式(7)、(8)平方后相加得

x2+y2=v10xy2t2

(9)

为了便于研究，把篮板分成6份(图6).

图6 篮板尺寸、打板点位置及坐标

正对篮板右侧的两份中找出6个非常规打板点(图6上1，2，3，4，5，6点)，篮球从这6个打板点的某一点打板反弹后落入篮筐，入筐时质心与篮筐的圆心重合(即空心入篮)，篮筐的坐标点在篮筐圆心．假设，篮球的质心在球心，当篮球打在篮板上时，篮球质心的Y坐标为0.121 3 m，根据观察凯里·欧文篮下侧旋打板投篮的视频，用秒表多次计时估算出低、中、高6个打板点从打板到进筐时间t的平均值分别为0.30 s，0.35 s，0.40 s．本文暂不分析篮球打板后与篮圈发生碰撞的进筐情况．

图6中1，2，3，4，5，6点为选定点，x，y，z的值是已知的，这6点为坐标原点时，篮球运动的x，y，z数值已知．篮球的半径按照男子成年篮球7号球的国家标准为0.121 3 m，计算中取3位小数为0.121，数值Y=0.150+0.225-0.121=0.254 m．将上述数据代入式(9)，计算出篮球顺时针侧旋转(从球的上方向下看)时水平方向的分速度v10xy的值．

将计算出的v10xy值，与已知的t，x或y值代入到式(7)或式(8)中计算出θ．将z，t，g(9.8)的值代入(4)中求出v10z．由v10xy，v10z求出v10．

前面式(1)中，r取值为0.121 m，算出ω1的最小值如表1所示.

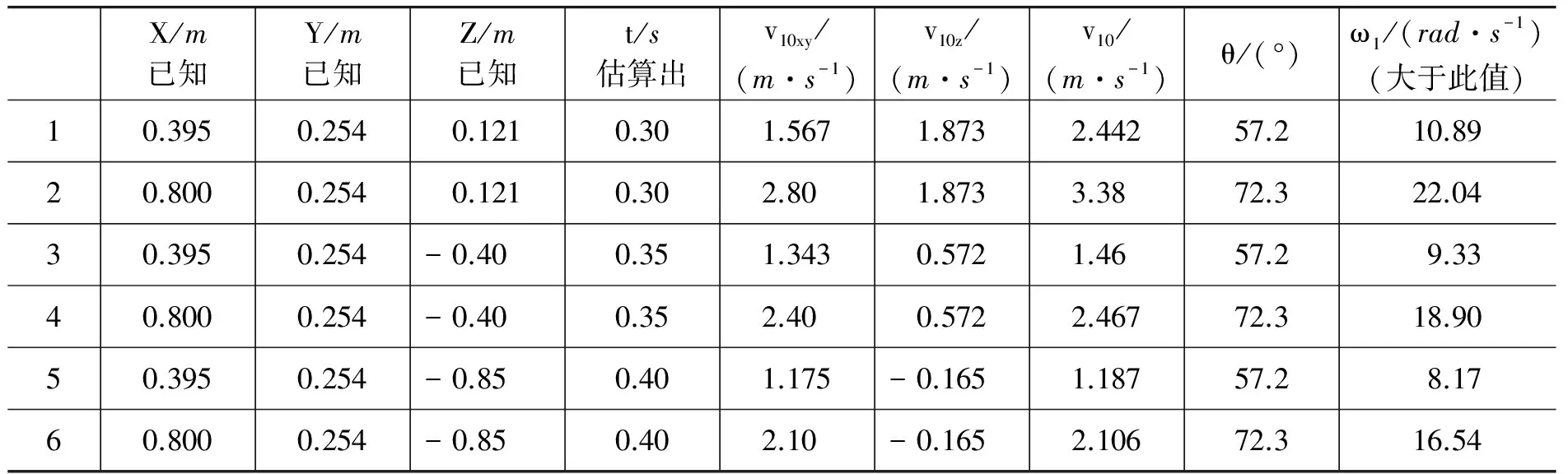
表1 计算数据

水平距离接近篮筐的1，3，5的3个点的角速度值相对较小，5点的值最小，不少于8.17 r/s，即篮球侧旋转468.30°/s，相当于篮球最少旋转1.3 r/s；水平距离相对远离篮筐的2，4，6这3个点的角速度值相对较大，2点的值最大，不小于22.04 r/s，即篮球侧旋转1 263.33°/s，相当于篮球最少旋转3.5 r/s．

为了印证数据的合理性，笔者在篮球上面用红色的纸条做个标记，用透明胶带粘牢，模拟篮下旋转投篮动作，尽自己最大力量将篮球顺时针侧旋，并向正上方抛出(高度2 m左右)，同时用手机记录下视频．在电脑上用视频软件慢速播放，可以看清红色标记转动的圈数，记下所需时间，计算后的数值约为5.6 r/s，作为有一定基础的篮球爱好者来说这个转速基本上接近极限．实际测试的侧旋转角速度数值与上面推算的角速度取值范围基本一致，计算出的篮球打板反弹后的速度v10值与凯里·欧文篮球视频中的演示情况也基本相符，作为一名普通篮球爱好者在实战中完全能做到，可行性较强．

5 结论

本文通过构建理想化模型，采用逆推的方法，对

篮下侧旋打板投篮进行了定量分析，研究后得知，篮下打板投篮时，篮球以一定的角速度侧向旋转，篮球受到篮板施加的摩擦力(方向与球触篮板的侧旋方向相反)作用下，反弹方向发生偏移，使篮球按照理想方向进入篮筐，增大了篮下打板区域的选择和投篮的命中率．一般情况下，在篮筐的右侧(面对篮板)投篮，球应按竖直方向左旋(从上向下看顺时针方向)；在篮筐的左侧投篮，球应按竖直方向右旋；投篮时打板点离篮筐水平距离越远，要求篮球旋转的角速度越大．而在现实中篮下侧旋打板投篮，篮球与篮筐碰撞后进筐等非理想化情况是占多数，打板点位置也几乎无禁区，因此，表1中篮球的角速度、速度等数据的选择也不是唯一的，允许有一定的取值范围，作为一名普通篮球爱好者通过平时的训练是完全可以掌握的，进而为探索打板投篮训练、提高投篮命中率提供了一定的理论指导．通过本文的探究，令广大球迷羡慕的凯里·欧文式打板投篮不再是高不可及的神奇“法宝”．

参 考 文 献

1 钟锡华, 周岳明.力学 . 北京: 北京大学出版社, 2012. 23～24,121～158

2 孙春峰，杨小云. 旋转球与非旋转球运动的力学原理.孝感学院学报，2003(5)：36～39

3 葛隆祺，叶卫军． 足球旋转球的运动规律．物理通报，1999，18(2):7～8

4 王成军，郑 旗. 篮球的旋转对提高投篮命中率的力学分析体育研究与教育，2012(4)：100～104

5 曹则贤．足球也科学: 力道与旋转．物理，2010，39( 7): 480～481

短文荟萃