射孔水压裂缝在层状页岩的扩展机制
王海洋, 卢义玉, 夏彬伟, 龚 涛, 张 睿
(1.重庆大学煤矿灾害动力学与控制国家重点实验室,重庆 400030; 2.重庆交通大学土木工程学院,重庆 400074;3.中煤科工集团重庆研究院有限公司,重庆 400037)
页岩气是一种重要的非常规战略能源,产自极低孔渗、以富有机质页岩为主的储集岩系中[1]。用于页岩储层渗透率改造的水力压裂技术是页岩气开发的核心技术之一,其中的水平井射孔分段压裂技术作为高效开发页岩气的重要手段,日益得到广泛应用[2]。Abass[3]认为定向射孔可降低水力压裂中出现分支缝、T型缝和弯曲缝的几率。Zhang等[4]通过研究发现射孔密度和射孔方位角是影响起裂压力的主要因素;李根生等[5]建立了包含地层-水泥环-套管的水力射孔井的三维力学模型,研究发现射孔深度的增加可有效降低地层的破裂压力;黄中伟等[6]通过实验研究发现射孔后的起裂压力随射孔深度和直径的增大而减小,随射孔轴线和最大水平应力方向夹角的增大而增大。对于水压裂缝与层理面相交后的扩展规律,Hanson、Anderson等[7-8]开展了层间界面性质对裂缝垂向扩展影响规律的试验研究;衡帅等[9]研究了层理对页岩水力裂缝扩展的影响及层理在页岩网状裂缝形成过程中的作用;夏彬伟等[10]研究了水压裂缝遇断层面后的扩展规律及影响因素,主要考察了逼近角度、水平主应力差、煤岩体弹性模量等因素;宋晨鹏等[11]对水压裂缝遇煤岩交界面的破坏机制及压裂裂缝扩展规律进行了研究。水压裂缝在页岩及层状地层的扩展方面,李传华等[12]通过层状介质水力压裂模拟试验,分析了垂向应力、弹性模量、断裂韧性和界面胶结状况等因素对裂缝是否穿透隔层的影响;李庆彬[13]研究了垂直裂缝遇砂/泥岩界面的扩展规律,重点考察了层间岩性差异、层理面强度对水压裂缝扩展的影响;潘林华等[14]建立了二维网状裂缝扩展有限元模型,研究了水平主应力差、施工排量对页岩储层复杂裂缝的扩展规律;李志超[15]的研究发现,地应力差与射孔方位角越大,压裂裂缝从井壁位置起裂的可能性越大,而从射孔方向起裂的几率降低。张士诚等[16]采用大尺寸真三轴试验系统开展了水力裂缝在页岩扩展的模拟试验,研究了排量、水平地应力差和压裂液黏度等因素对页岩水平井压裂裂缝扩展规律的影响。水压裂缝在层状岩层中的扩展,主要受应力差、层间岩性差异、层理面性质等因素的影响。在层状页岩中,当射孔方向与最大主应力方向存在一定夹角,水压裂缝将会向最大主应力方向发生偏转,偏转裂缝在遇页岩层理面时的扩展规律是影响页岩储层网状裂缝形成的重要因素,而目前对于偏转裂缝在遇页岩层理面时的扩展规律及影响因素还缺乏系统深入研究。笔者从水压裂缝尖端应力场、水压裂缝偏转角及水压裂缝与层理面相交后的应力场等方面建立偏转裂缝在层状页岩扩展的应力分析模型,并对偏转裂缝遇层理面后的扩展方向及影响因素进行分析,进而结合数值模拟,研究对不同主应力差、层理面角度、射孔角度和层理面黏聚力条件下偏转裂缝遇层理面后的扩展规律。
1 射孔水压裂缝在层状页岩的扩展模型
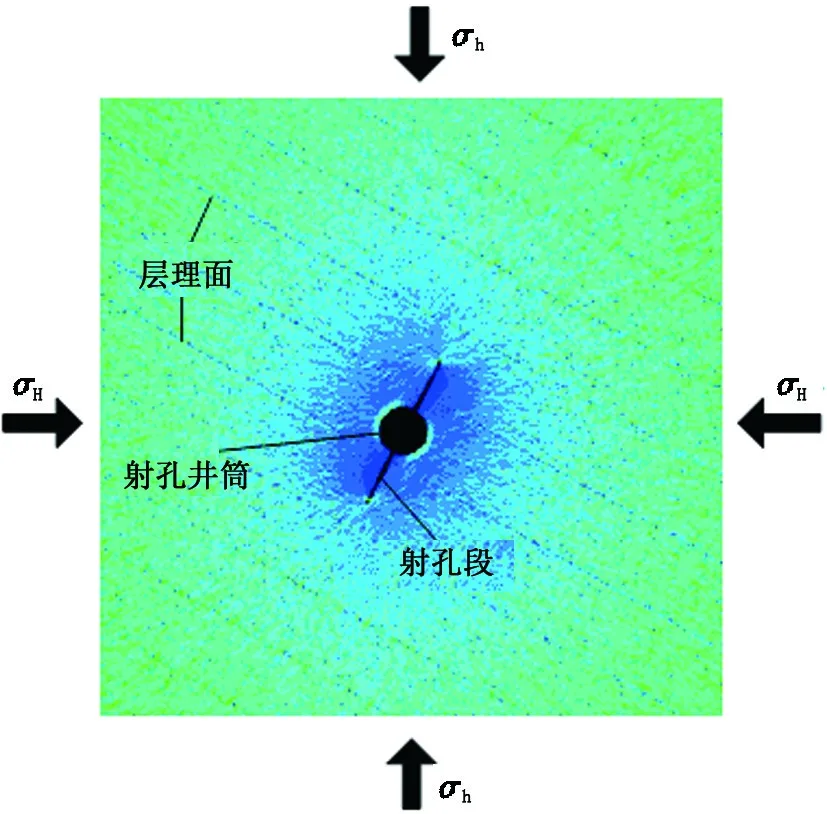
在无外界因素干扰情况下,水力压裂在均质地层中通常会形成垂直于最小水平主地应力方向扩展的垂直裂缝,而水力射孔则人为改变了水力压裂的初始起裂及扩展方向,产生的水压裂缝会向最大主应力方向发生偏转,为此建立如图1所示的射孔水压裂缝在层状页岩的扩展模型,其中σH为最大水平主地应力,MPa;σh为最小水平主地应力,MPa;α1为层理面与最大主应力方向夹角;α2为射孔方向与最大主应力方向夹角;α3为裂缝偏转方向与射孔方向夹角;α4为偏转裂缝与层理面的相交角;α、r分别为射孔段长度和偏转裂缝长度,m。
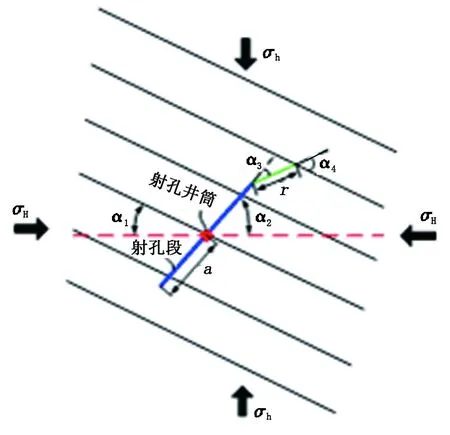
图1 射孔水压裂缝在层状页岩的扩展模型Fig.1 Propagation model of hydraulic fracture of perforation in laminated slate
2 偏转裂缝在层状页岩扩展的应力分析模型
力学分析模型的构建和数值模型的计算遵循如下基本假设:
(1) 页岩的层理面角度、间距一致;
(2) 层理面、层理面间的岩石是均质的;
(3) 建立的模型所受加载应力均匀。
2.1 水压裂缝尖端应力场
根据二维线弹性理论[17],远场地应力在水力射孔裂缝面上形成的正应力和剪应力分别为
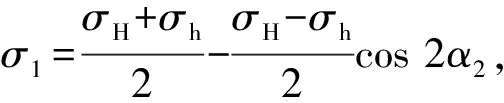
(1)
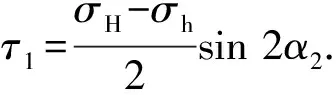
(2)
在远场地应力及内水压力的作用下,射孔裂缝面上的正应力和剪应力分别为
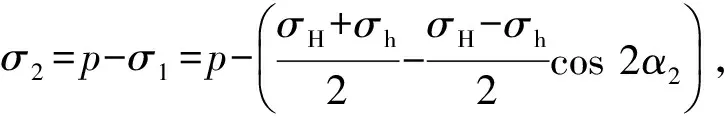
(3)
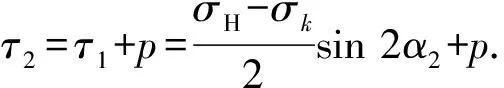
(4)
式中,p为裂缝内水压力,MPa。
根据断裂力学理论,偏转裂缝不沿初始裂纹面扩展,而是沿分支裂纹面扩展,属于KⅠ-KⅡ复合型裂纹,裂缝尖端的应力强度因子为

(5)
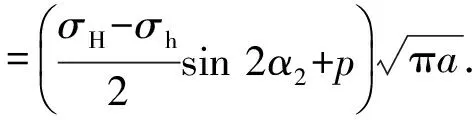
(6)
由式(5)和(6),裂缝尖端应力场的极坐标表达式为
(7)
式中,σrr、σθθ和σrθ为裂纹尖端极坐标应力分量。
2.2 水压裂缝偏转角
根据最大正应力准则,裂纹沿周向正应力达到最大的方向扩展,故裂缝扩展方向可式确定为
整理可得:KⅠsinα3+KⅡ(3cosα3-1)=0。
进而可求得
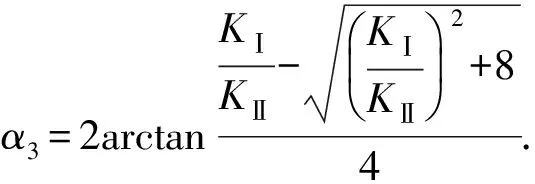
(8)
将式(5)、(6)代入式(8),整理得
(9)
由式(9)发现,水压裂缝的偏转角主要与裂缝内水压、水平主应力差、射孔角度等因素有关,而不受射孔长度的影响。
偏转裂缝与层理面的相交角α4可表示为
α4=π-α1-α2-α3.
(10)
因此,偏转裂缝与层理面的相交角除了与裂缝内水压、水平主应力差、射孔角度等因素有关外,还取决于层理面的角度。
2.3 水压裂缝与层理面相交后的应力场
在远场地应力作用下,层理面上的正应力与剪应力可以表示为
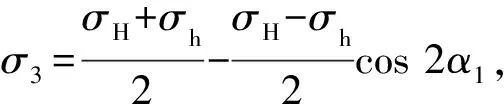
(11)
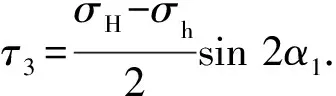
(12)
在远场应力及内水压力的作用下,层理面上的正应力与剪应力表示为
σ4=σ3-σθθ,
(13)
τ4=τ3+σrθ.
(14)
将式(7)、(11)、(12)代入式(13)、(14)即可得出水压裂缝与层理面相交后的正应力与剪应力表达式。
3 偏转裂缝遇层理面后的扩展方向
由于射孔方向与最大主应力方向呈一定夹角,故射孔后的水压裂缝在扩展过程中会发生偏转,当偏转裂缝与层理面相交后,会发生3种可能的扩展情况:①裂缝沿层理面扩展;②裂缝穿过层理面扩展;③裂缝分叉,部分穿过层理面扩展,部分沿层理面扩展。
当复合应力强度因子(K12)达到临界值,即K12=KⅠC时,裂纹就开始扩展。K12、KⅠC的表达式[18]为
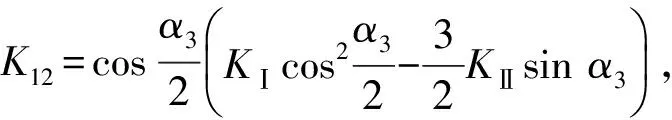
(15)
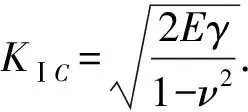
(16)
式中,E为页岩的弹性模量,MPa;γ为页岩的单位面积表面能,MPa·m;ν为页岩的弹性模量、泊松比。
将式(5)、(6)代入式(15)、(16),整理可得裂缝在岩石中扩展的临界水压p1;在τ4>C时,层理面发生剪切破坏,整理可得裂缝在层理面扩展的临界水压p2,p1和p2的表达式为
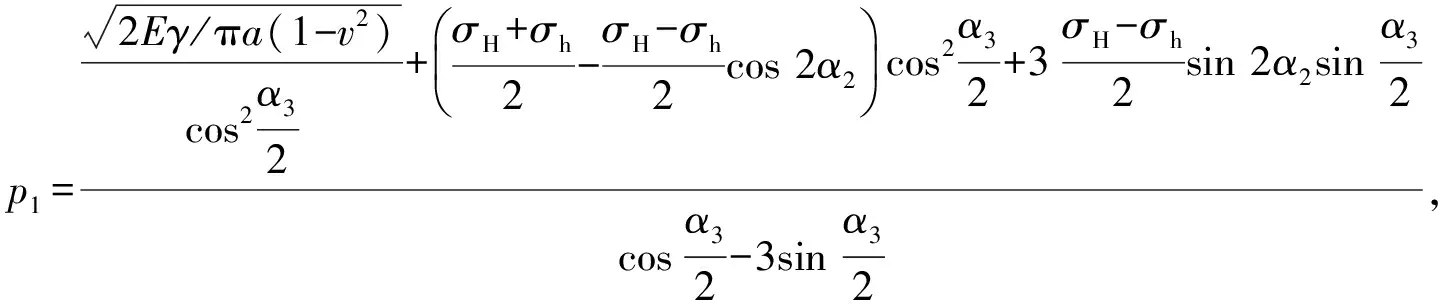
(17)
(18)
式中,C为层理面的黏聚力,MPa。
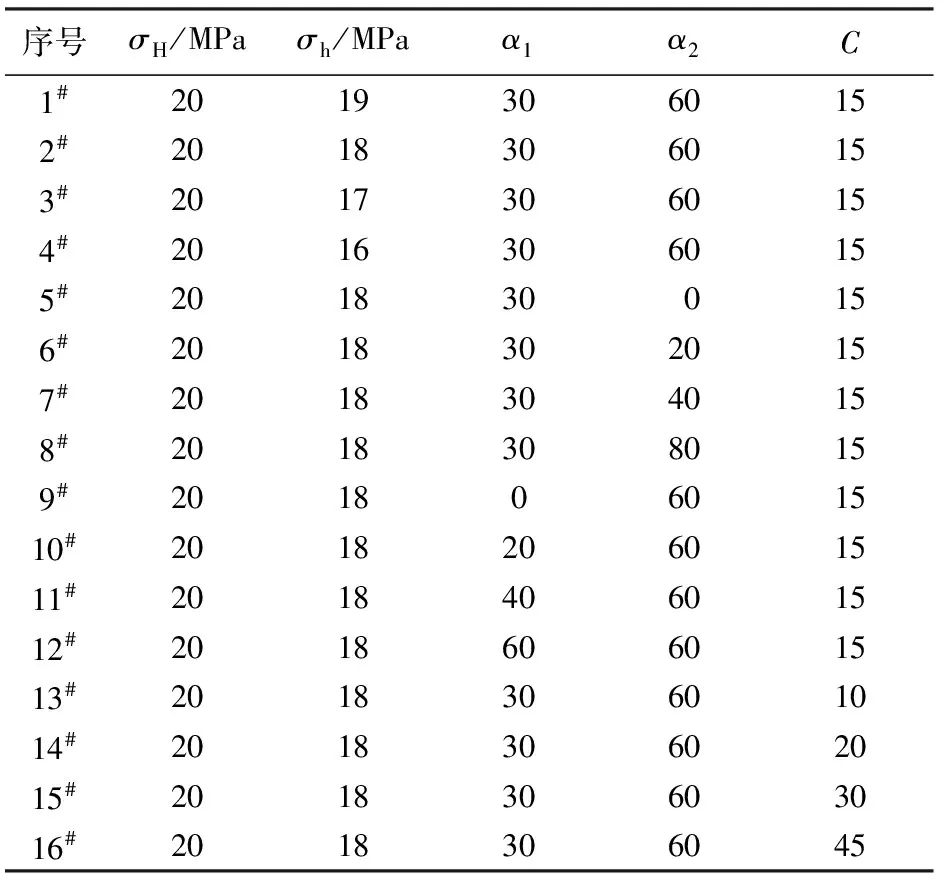
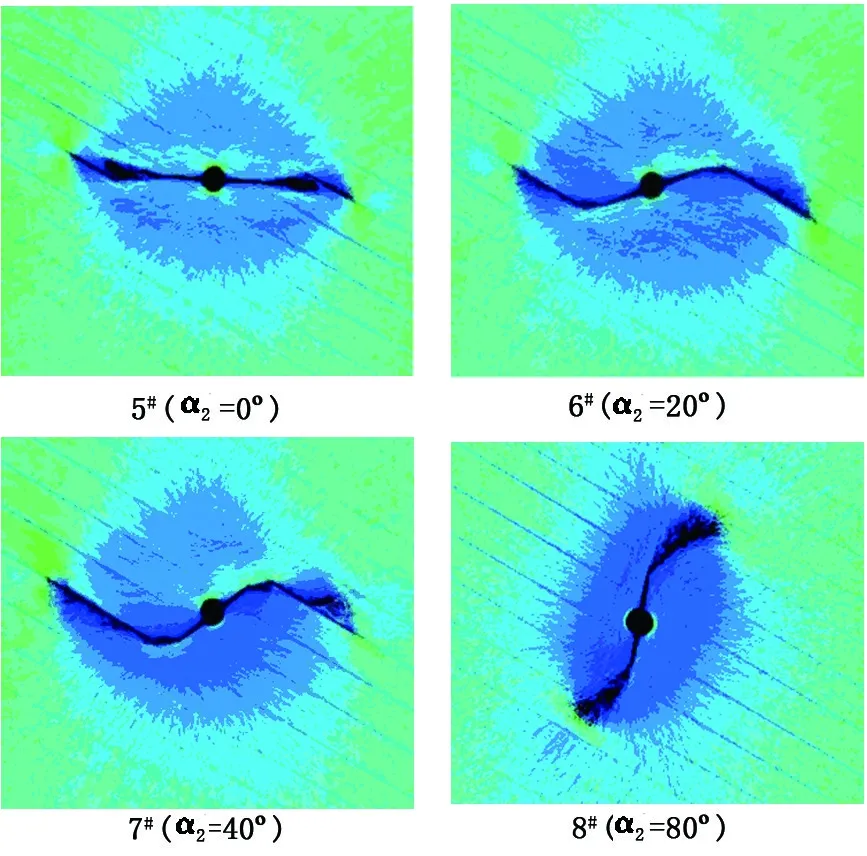
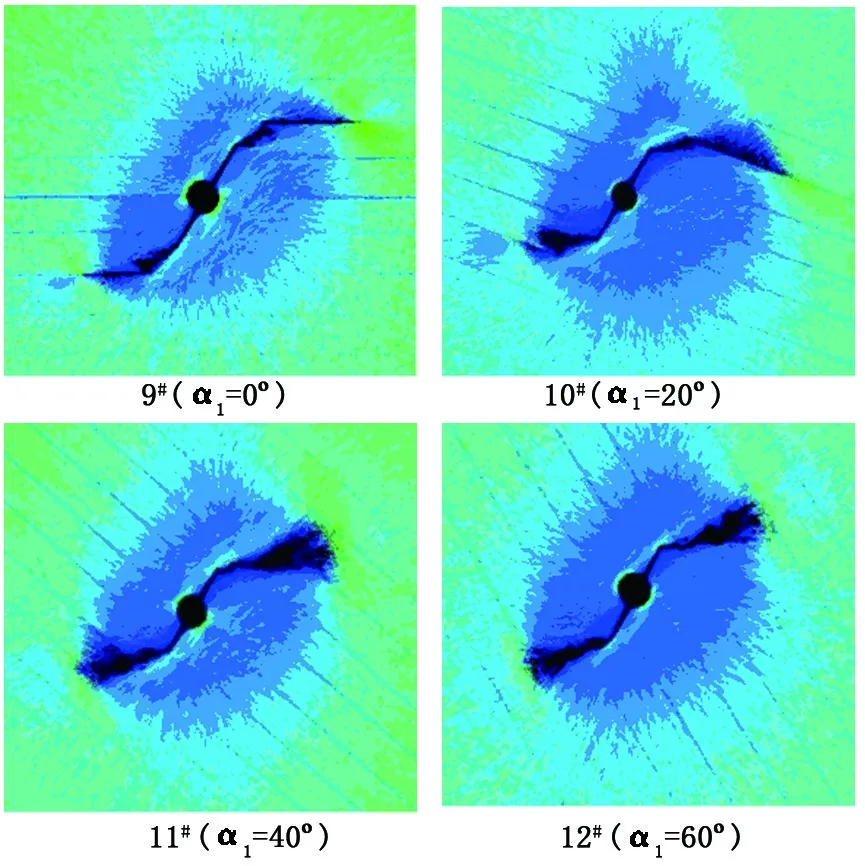
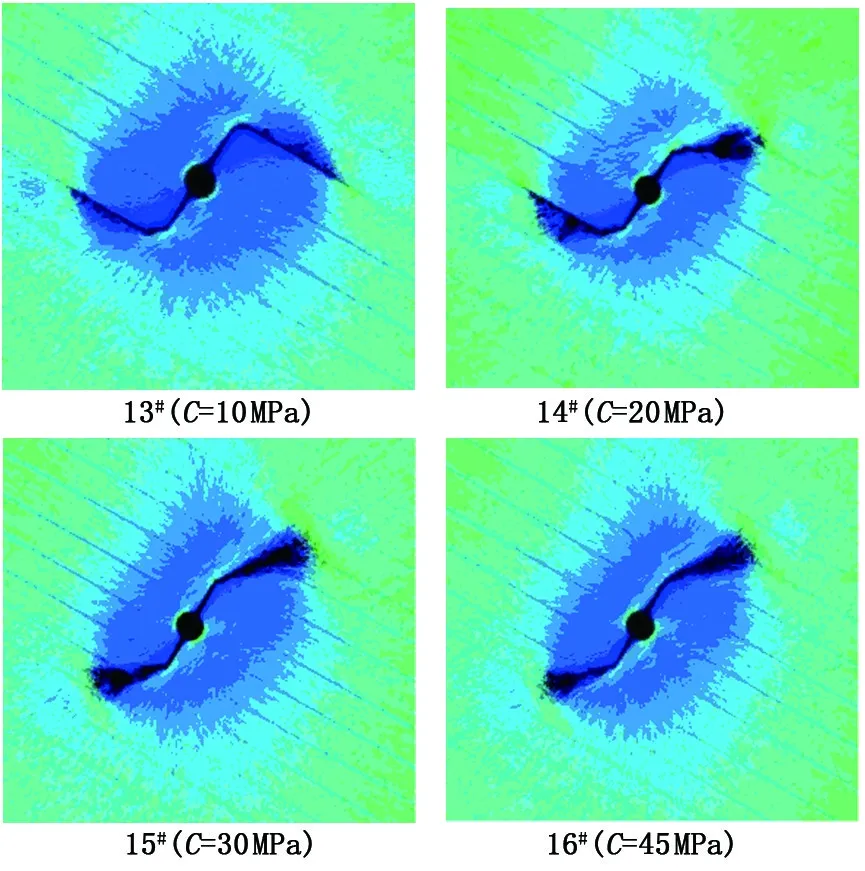
由此可以确定,当p1 采用岩石破裂失稳的渗流应力耦合分析系统RFPA2D-Flow,对射孔水压裂缝遇页岩层理面的扩展规律进行数值模拟。 建立如图2所示的数值分析模型,模型尺寸5 m×5 m,划分为500×500=250 000个单元,将模型的水平地应力以位移边界条件的方式施加于模型的两边,模型中建立倾斜条带表示页岩层理面,在模型中部设置一个射孔井筒,井筒套管内径、外径分别为0.12和0.15 m,在井孔两端对称位置各开一个长度为0.4 m的射孔,射孔井筒套管的强度及弹性模量均高于页岩,模型施加的初始水压为20 MPa,单步增量为0.05 MPa。 图2 数值分析模型Fig.2 Numerical analysis model 依据四川省宜宾市下志留统龙马溪组页岩试样的实验室测试结果,确定页岩储层物理力学参数如表1所示。 表1 页岩储层参数设置 为考察不同水平主应力差、层理面角度、射孔角度和层理面黏聚力对偏转裂缝扩展的影响,根据目前页岩压裂的现场条件及文献[19],制定了如表2所示的数值模拟方案。考虑到篇幅,数值模拟方案仅考虑了层理面角度和射孔角度在0~90°的情况。 表2 数值模拟方案 图3 水平主应力差的影响Fig.3 Influence of principal stress difference (1)水平主应力差。不同水平主应力差对偏转裂缝扩展的影响如图3所示。可以看出,水平主应力差的变化对偏转裂缝的扩展影响显著,随着水平主应力差的增加,水压裂缝的偏转角不断增大,偏转裂缝由最初的直接穿过页岩层理面逐渐转化为沿层理面扩展,在水平主应力差为2、3 MPa时,偏转裂缝可同时穿过层理面和沿层理面扩展,但是裂缝穿过层理面的倾向性会随水平主应力差的增大明显弱化,而当水平主应力差为4 MPa时,裂缝直接在射孔段就沿层理面扩展。 (2)射孔角度。射孔角度对偏转裂缝扩展的影响如图4所示,结合第2#组数值模拟结果发现,在层理面角度与最大主应力方向保持不变时,偏转裂缝穿过层理面扩展的倾向性随射孔角度的增大而逐渐增加。在α1小于60°时,水压裂缝的整体扩展模式变化不大,始终以沿层理面扩展为主;在α1达到60°时,偏转裂缝穿过层理面扩展的倾向性明显增大;而当α1达到80°时,偏转裂缝则直接穿过层理面扩展。 图4 不同射孔角度的影响Fig.4 Influence of perforation angle (3)层理面角度。层理面角度对偏转裂缝扩展的影响如图5所示,结合第2#组数值模拟结果,可以发现,随着层理面与最大主应力方向夹角的增大,水压裂缝由沿层理面扩展逐渐转变为直接穿过层理面扩展,当α1为10°、20°时,裂缝可同时穿过层理面和沿岩层理面扩展,但是裂缝沿层理面扩展的倾向性明显占优势;而当α1增大到30°时,裂缝穿过层理面扩展的倾向性明显增大;在α1超过40°时,裂缝仅穿过层理面扩展。 (4)层理面黏聚力。层理面黏聚力对偏转裂缝扩展的影响如图6所示,结合第2#组数值模拟结果发现,随层理面黏聚力的增大,水压裂缝的扩展模式由沿层理面扩展逐渐转变为直接穿过层理面扩展,在层理面黏聚力为15、20 MPa时,偏转裂缝同时沿层理面和穿过层理面扩展,但前者以沿层理面扩展为主,而后者以穿过层理面扩展为主,当层理面黏聚力达到30 MPa及以上时,偏转裂缝扩展模式保持不变,即直接穿过层理面扩展。 图5 层理面角度的影响Fig.5 Influence of bedding plane angle 图6 层理面黏聚力的影响Fig.6 Influence of bedding plane cohesion (1)基于弹性力学和断裂力学相关理论建立射孔水压裂缝在层状页岩扩展的应力分析模型,得到水压裂缝偏转角及偏转裂缝在页岩和层理面扩展的临界水压的表达式。 (2)水压裂缝的偏转角主要与裂缝内水压、最大及最小水平主应力、射孔角度等因素有关,而不受射孔长度的影响,偏转裂缝与层理面的相交角还取决于层理面的角度。偏转裂缝与页岩层理面的扩展模式,尤其是水平主应力差、射孔角度、层理面角度、页岩力学性质及层理面黏聚力等因素有关。 (3)若最大水平主应力方向与层理面夹角不大,随水平主应力差的增大,偏转裂缝由直接穿过层理面逐渐转化为沿层理面扩展,当主应力差增加到一定程度后,水压裂缝极易在射孔段与层理面的相交处发生起裂并沿层理面扩展。 (4)随着射孔角度、层理面角度、层理面黏聚力的增大,偏转裂缝穿过层理面扩展的倾向性逐渐增加,扩展模式由最初的沿层理面扩展逐渐转变为直接穿过层理面扩展。若最大水平主应力方向与层理面存在一定的夹角,射孔段与层理面的夹角越接近90°,偏转裂缝同时穿过层理面和沿层理面扩展的倾向性越大,越易于在页岩储层中形成网状裂缝。 参考文献: [1] ROSS D J K, BUSTIN R M. Characterizing the shale gas resource potential of devonian:mississippian strata in the Western Canada sedimentary basin: application of an integrated formation evaluation [J]. AAPG Bulletin, 2008,92(1):87-125. [2] CUDERMAN J F, NORTHROM D A. A propellant-based technology for multiple-fracturing wellbores to enhance gas recovery: application and results in Devonian shale [J]. SPE Production Engineering, 1986,1(2):97-103. [3] ABASS H H. Oriented perforating helps ensure successful well completions [J]. Oil and Gas Journal, 1995,93(41):80-85. [4] ZHANG G Q, CHEN M, WANG X S, et al. Influence of perforation on formation fracturing pressure [J]. Petroleum Science, 2004,1(3):56-61. [5] 李根生,刘丽,黄中伟,等.水力射孔对地层破裂压力的影响研究[J].中国石油大学学报(自然科学版),2006,30(5):42-45. LI Gensheng, LIU Li, HUANG Zhongwei, et al. Study of effect of hydraulic perforating on formation fracturing pressure[J]. Journal of China University of Petroleum (Edition of Natural Science), 2006,30(5):42-45. [6] 黄中伟,李根生.水力射孔参数对起裂压力影响的实验研究[J].中国石油大学学报(自然科学版),2007,31(6):48-54. HUANG Zhongwei, LI Gensheng. Experimental study on effects of hydrau-perforation parameters on initial fracturing pressure [J]. Journal of China University of Petroleum (Edition of Natural Science), 2007,31(6):48-54. [7] HANSON M E, SHAFFER R J. Some results from continuum mechanics analyses of the hydraulic fracturing process [J]. Society of Petroleum Engineers Journal, 1980,20(2):86-94. [8] ANDERSON G D. Effects of friction on hydraulic fracture growth near unbonded interfaces in rocks [J]. Society of Petroleum Engineers Journal, 1981,21(1):21-29. [9] 衡帅,杨春和,郭印同,等.层理对页岩水力裂缝扩展的影响研究[J].岩石力学与工程学报,2015,34(2):228-237. HENG Shuai, YANG Chunhe, GUO Yintong, et al. Influence of bedding planes on hydraulic fracture propagation in shale formations [J]. Chinese Journal of Rock Mechanics and Engineering, 2015,34(2):228-237. [10] 夏彬伟,杨冲,卢义玉,等.断层对煤层水力压裂裂缝扩展的影响[J].中国石油大学学报(自然科学版),2016,40(1):92-99. XIA Binwei, YANG Chong, LU Yiyu, et al. Effect of faults on hydraulic fracture propagation in coal seam [J]. Journal of China University of Petroleum (Edition of Natural Science), 2016,40(1):92-99. [11] 宋晨鹏,卢义玉,贾云中,等.煤岩交界面对水力压裂裂缝扩展的影响[J].东北大学学报(自然科学版),2014,35(9):1340-1345. SONG Chenpeng, LU Yiyu, JIA Yunzhong, et al. Effect of coal-rock interface on hydraulic fracturing propagation [J]. Journal of Northeastern University(Natural Science), 2014,35(9):1340-1345. [12] 李传华,陈勉,金衍.层状介质水力压裂模拟实验研究[C]//中国岩石力学与工程学会第七次学术大会.北京:中国科学技术出版社,2002:111-113. [13] 李庆彬.砂/泥岩界面垂直裂缝扩展规律研究[D].大庆:东北石油大学,2013. LI Qingbin. Vertical crack propagation law research of sand/mudstone interface [D]. Daqing: Northeast Petroleum University, 2013. [14] 潘林华,张烨,陆朝晖,等.页岩储层复杂裂缝扩展研究[J].断块油气田,2016,23(1):90-94. PAN Linhua, ZHANG Ye, LU Zhaohui, et al. Complex fracture propagation in shale gas reservoir [J]. Fault-Block Oil & Gas Field, 2016,23(1):90-94. [15] 李志超.页岩储层水平井水力裂缝起裂与扩展特征的数值模拟分析[D].大连:大连理工大学,2015. LI Zhichao. Numerical investigation on hydraulic fracture initiation and propagation behavior in horizontal wells of shale reservoir [D]. Dalian: Dalian University of Technology, 2015. [16] 张士诚,郭天魁,周彤,等.天然页岩压裂裂缝扩展机理试验[J].石油学报,2014,35(3):496-503. ZHANG Shicheng, GUO Tiankui, ZHOU Tong, et al. Fracture propagation mechanism experiment of hydraulic fracturing in natural shale [J]. Acta Petrolei Sinica, 2014,35(3):496-503. [17] 吴家龙.弹性力学[M].北京:高等教育出版社,2001. [18] 王自强,陈少华.高等断裂力学[M].北京:高等教育出版社,2009. [19] 邓金根,陈峥嵘,耿亚楠,等.页岩储层地应力预测模型的建立和求解[J].中国石油大学学报(自然科学版),2013,37(6):59-64. DENG Jingen, CHEN Zhengrong, GENG Yanan, et al. Prediction model for in-situ formation stress in shale reservoirs[J]. Journal of China University of Petroleum (Edition of Natural Science), 2013,37(6):59-64.4 偏转裂缝遇页岩层理面数值模拟
4.1 模型构建及参数设置

4.2 数值模拟方案
4.3 数值模拟结果分析

5 结 论

