利用CATIA进行十字万向节力矩传递分析

殷腾蛟，甘林

（安徽江淮汽车集团股份有限公司，安徽 合肥 230022）

前言

利用CATIA软件的运动分析功能，可以模拟出任意时刻输入轴、输出轴、十字轴的位置关系，利用位置关系数据，可以直接计算出输入轴与输出轴之间的力矩关系。

1 十字万向节力矩传递分析

1.1 任意时刻下力矩分析

1.1.1 十字万向节传动机构

任意时刻时，十字万向节传动机构如下图1所示：

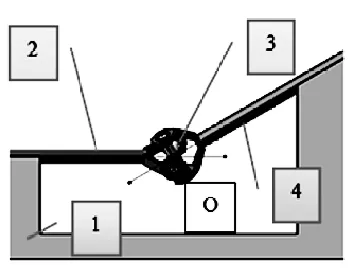
图1 十字万向节传动机构

其中：1、基座；2、输入轴；3、十字轴；4、输出轴。输入轴与输出轴交点为O。

1.1.2 输入轴对十字轴作用力分析

输入轴对十字轴受力分析如下图2所示：

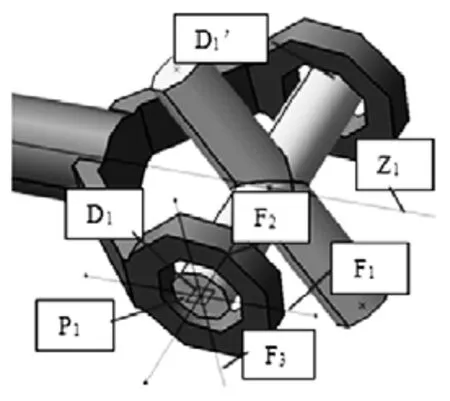
图2 输入轴对十字轴受力分析

D1、D1’为力的作用点。轴线 Z1与输入轴轴线重合，通过 D1与 Z1做平面 P1，过 D1做 3条正交直线 F1、F2、F3表示3个方向的力，F1与轴线平行，F3为P1的法线。D1上的力未知，可以用 F1、F2、F3三个方向的力表示。D1’按照 D1的方式处理。D1、D1’的合力对十字轴产生的力矩如下图 3所示：

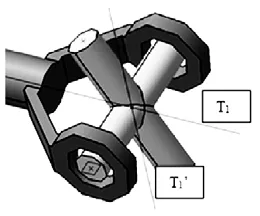
图3 D1、D1’的合力对十字轴产生的力矩

T1与轴线Z1平行，T1’为P1的法线方向，T1、T1’垂直。根据作用力与反作用力的关系，十字轴对输入轴轴线方向的力矩大小同 T1，因输入轴力矩平衡，所以 T1大小等于输入力矩大小。

1.1.3 输出轴对十字轴作用力分析

输出轴对十字轴受力分析如下图4所示：

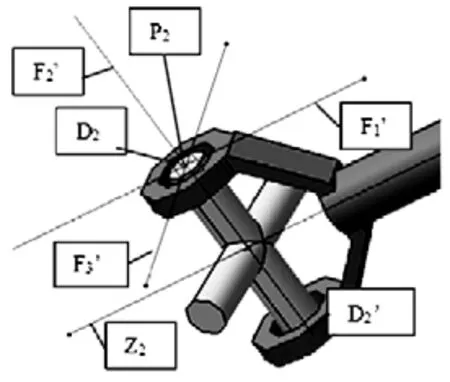
图4 输出轴对十字轴受力分析

分析方法同输入轴对十字轴的受力分析，其中Z2为输出轴轴线，D2、D2’为输出轴对十字轴力的作用点，平面 P2通过D2、D2’与Z2。D2、D2’的合力对十字轴产生的力矩如下图5所示：

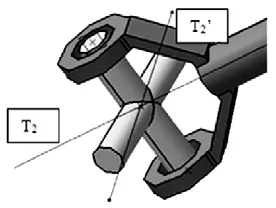
图5 D2、D2’的合力对十字轴产生的力矩

T2与轴线 Z2平行，T2’为 P2的法线方向，T2、T2’垂直。根据作用力与反作用力的关系，十字轴对输出轴轴线方向的力矩大小同 T2，因输出轴力矩平衡，所以 T2大小等于输出力矩大小。

1.1.4 计算T1与T2的关系

根据以上分析，十字轴受力矩图如下图6所示：

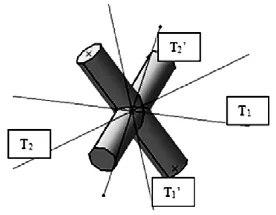
图6 十字轴受力矩图

通过十字轴轴线X1与X2做平面P3，过O点做P3的法线Z3，如下图7所示：

图7 做十字轴平面与法线

通过前面做图方式可知，X1同时与 Z3、T1、T1’垂直，X2同时与 Z3、T2、T2’垂直，即 Z3、T1、T1’共面，Z3、T2、T2’共面。

将T1、T1’向Z3方向求合力矩为T3，如下图8所示，将T2、T2’向Z3方向求合力矩为T3’，如下图9所示：

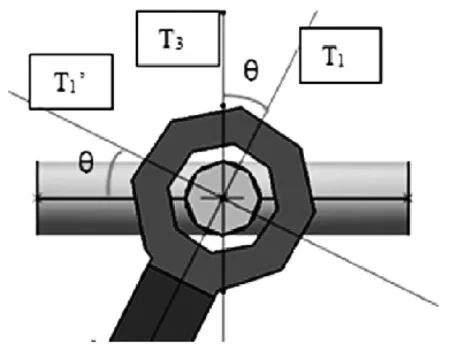
图8 T1、T1’向Z3方向求合力矩为T3

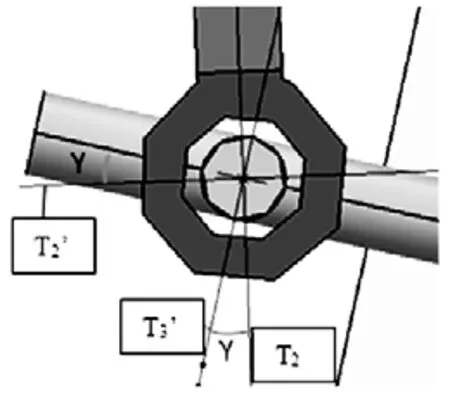
图 9 T2、T2’向 Z3方向求合力矩为 T3’

角度θ、γ可通过CATIA软件运动分析功能计算出来。角度θ即为输入轴节叉相对于十字轴转过的角度，角度γ即为输出轴节叉相对于十字轴转过的角度。

1.2 十字万向节运动过程中的力矩传递分析

因输入轴旋转一周后回到初始状态，所以只需求出输入轴旋转一周过程中的角度θ、γ。具体步骤如下：

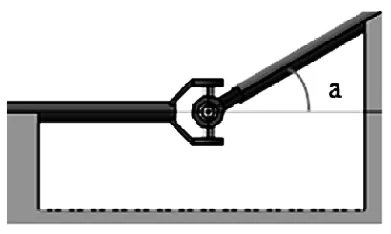
图10 初始状态

（1）设置初始状态如下图10所示，输入轴与输出轴夹角a=30°，输入轴与十字轴平面P3垂直。

（2）设置输入按6°/s的角速度匀速转动；

（3）打开模拟器，打开传感器，将输入轴与万向节夹角、输出轴与万向节夹角两项设定为能观察到，如下图11所示：

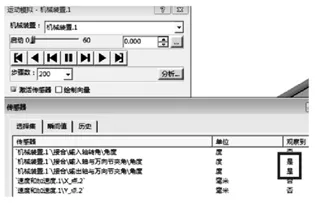
图11 模拟器选项

（4）运行

（5）运行完成后，点击传感器的图形选项，可以看到角度△θ、△γ的曲线如下图12所示。将结果输出到表格文件中。

θ=△θ+θ0，γ=△γ+γ0，θ0=0°，γ0=30°。

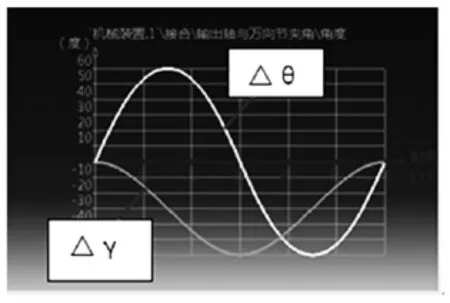
图12 运行结果

（6）设定输入力矩T入=1，将输出结果带入公式6，计算输出力矩T出，同时按照《汽车底盘设计》公式。

T出=T入*(1-SIN2a*COS2φ）/COSa计算出输出力矩 T出’，然后对比T出与T出’，对比结果如下图13所示，两个结果相同，曲线重合。

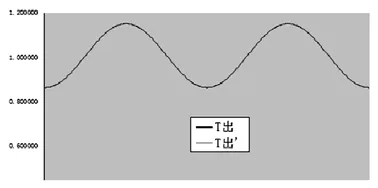
图13 对比T出与T出’

2 结论

通过对比，T出与T出’相同，说明以上分析方法准确可靠。可以将该分析方法运用到其它结构的受力分析中。

参考文献

[1] 王霄峰.汽车底盘设计.[M]北京.清华大学出版社,2010.

[2] 朱炳麒.理论力学.[M]北京.机械工业出版社,2001.

[3] 秦琳晶.CATIA V5R21完全实战技术手册.北京.清华大学出版社,2016.