基于开放式靶标的数学建模及传感器阵列分析
杜立
(总参第六十研究所机器人实验室,江苏南京210016)
根据空气动力学原理,当物体运动速度大于局部声速时产生激波。利用激波信号和传感器阵列检测超音速弹丸是极具挑战性的研究领域。近年来国内外涌现出大批研究成果,提出不同的传感器阵列方式,例如正四面体阵列[1],L型阵列[2],T型阵列[3,16],三角形[11]等等,传感器阵列方式不同,相应的数学模型也就不同。但现有的这些数学模型解析需要多种辅助条件或限制,如需要另加天幕靶测试弹丸速度[1-2],需要测量N波的时间宽度TF[2],射弹不超出立靶范围[2]等。本文所论述的数学模型,弥补以上缺点,利用5个以上的传感器排布即可解算得出弹丸速度,落点位置,入射角等参数。
在现实训练中开放式靶标的应用广泛,可用于各类口径的直瞄武器射击训练。训练中根据靶面的尺寸可分为单兵类、班组类和装甲类目标;根据靶标的出现方式可分为固定式、移动式和显隐式靶标。显隐式靶标又可分为起倒式、侧转式和升降式等多种显隐模式。各类靶标的安装防护要求各不相同,对靶标传感器的布阵方法也提出了多种方式,如平面 H 式[4-6]、垂面三角式[7,13]以及立体锥形[8,10]等。因此本文对各类传感器布阵方式进行了误差分析和优缺点总结,适当调整传感器阵列方式,可适应各种地形条件下的爆吧需求,为现代信息化条件下公安、武警、部队训练装备高精度低价格的训练设备提供有力的理论依据。
1 开放式靶标数学建模
1.1 基本测量原理
弹丸超音速飞行时,激波波前随着弹丸运动形成了以弹丸头部为顶点,弹道为轴线的圆锥体(如图1),弹道上每一点都可以看作点声源(俗称“砰发点”)。
将传感器按照一定方式阵列,当弹丸穿越传感器阵列附近时,弹丸激波引发传感器产生感应信号,且随着飞行位置不同,传感器接收到感应信号的时间不同。开放式靶标正是利用传感器采集激波信号,经过调理电路和运算电路测量出激波扫过不同传感器的时间间隔,在运用恰当的数学模型计算出弹丸通过靶面时的弹着点坐标、入射角、弹丸速度等参数。

图1 激波锥面示意图
1.2 单个传感器数学建模
如图2所示,P,A,B点均位于弹丸飞行轨迹上,其中B为子弹与靶面撞击点,P点为起始计时参考点,C点为某一传感器位置,A点为最早到达传感器C点的激波砰发点位置[4]。

图2 单个传感器数学模型
假设从P点初始计时,激波最先到达传感器C的总时间为t,包括子弹从P点到达A点的时间t1,和激波从A点到达C点的时间t2。AR为风速引发的矢量干扰,此时:t1=(1-λ)t,t2=λt
由图2得出:
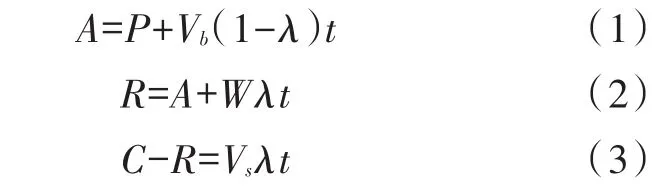
其中:Vb—弹丸飞行速度;W—风速;Vs—声速。
由(1)(2)(3)式联合求得:
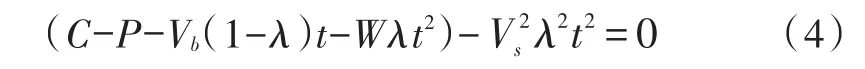
此时,令U=Vb-W、Q=P-C,等式(4)又可写为:

等式(5)对λ求偏导,令,化简等式为:

我们知道:Q=P-C,且P和B点均在弹丸飞行轨迹上,有:B=P+τ·Vb,由此得出:

将(7)式代入等式(6),得出:

式(8)是单个传感器方程,方程中未知数个数较多,必须通过传感器阵列,连立方程组进行求解。
1.3 传感器阵列解算建模
若认为子弹在接近靶面是水平入射,不考虑俯仰角,以靶面为XOZ平面,垂直靶面为Y轴,建立坐标系。排布若干传感器位置Ck(xk,yk,zk)(k=1,2,3,4,5…)(如图3),利用风速仪测得风速矢量(Wx,Wy,Wz),设撞击点B坐标(x,0,z),弹丸入射速度标量Vb,入射角度α,则可列出形如式(8)的若干方程式组,其中Vb,α,x,z,t-τ为未知量。
上述方程组为复杂的非线性方程组,没有解析解,必须借助特定的数学方法进行求解。现实开放式靶标系统中,我们可以借助电路系统测量得到激波到达若干传感器的时间差t21,t31,t41,t51,…,tk1,因此我们将式(8)简化为关于时间t的方程,求解过程中,我们将方程组写成矩阵和向量形式,其中未知量:

到达时间向量为:
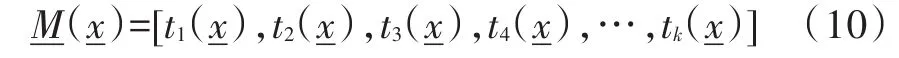
实测时间差向量为:

令雅克比矩阵H为:
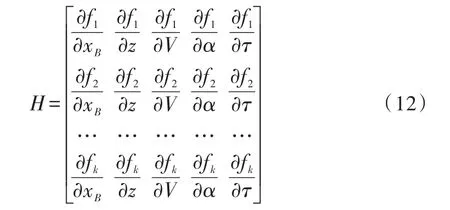
取一定的初始迭代值,假设弹丸速度700 m/s,垂直入射,落点位置为靶面中央高1 m的位置,即初始值为τ=0.5,α=0°,x=0,z=1,V=700,根据解非线性方程组的最小二乘广义逆法,进行迭代,得到最终结果。
算法中对于初始值的选取有要求,若初始值x坐标、弹丸速度V以及入射角α的选取与真实解相差太大,则会出现无穷大解。因此实际求解中我们采用区间搜索的方法进行迭代计算。将算法写成C代码,根据实际靶面大小划分125个区间,在计算机配置CPU主频3.4 G,内存512 MB的计算机中运行,将所有区间搜索完全需要15毫秒左右。而在实际计算中,一般在得到正确结果即终止搜索,运行时间完全满足实际报靶间隙要求。
2 传感器阵列方式的仿真分析
2.1 传感器阵列方式
如图3所示,在4×4米靶面的下方和前方阵列9个传感器(坐标位置见表1),将5个或以上传感器任意组合得到不同的阵列方式,均能得到计算结果。我们选取其中具代表性的3种布阵方式进行仿真分析。具体组合方式见表2。

图3 子弹入射与传感器阵列示意图
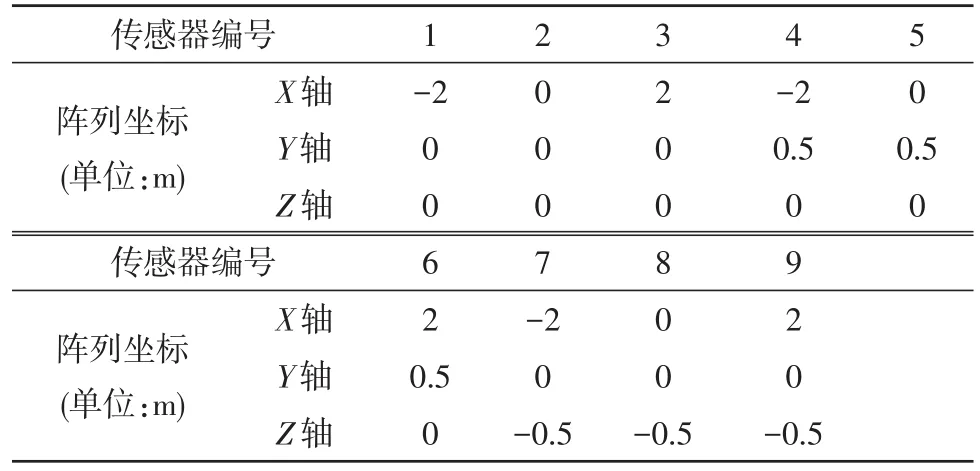
表1 传感器阵列坐标对应表
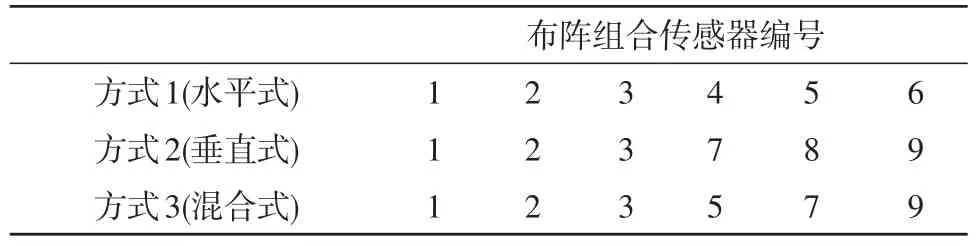
表2 代表性布阵组合方式
2.2 误差分析
利用Matlab仿真,将4 m×4 m靶面10×10等分,取每个等分区域中心点为落点位置,计算此时各传感器的TDOA时间。若弹丸垂直入射,假设入射速度800 m/s,入射角度0°,对此条件下的TDOA时间添加均方根为10 μs的时延误差。

图4 垂直靶面入射定位误差对比图(入射速度800 m/s,入射角度0°,TDOA误差10 μs)
图4为该射击条件下3种阵列方式中时延误差导致的定位误差等高线对比图,可见:
1)图4(a)为水平H阵列,靶面60%的落点坐标定位误差在1 cm以内,最大误差约2 cm。
2)图4(b)为垂直H阵列,靶面40%的落点坐标定位误差在1 cm以内,最大误差约4 cm。
3)图4(c)为混合式阵列,靶面80%的落点坐标定位误差在1 cm以内,最大误差约1 cm。
(入射速度 800 m/s,入射角度 45°,TDOA误差10 μs)
若弹丸角度入射,仍然假设靶面4 m×4 m,将上述条件中的弹丸入射角度修改为45°,入射速度仍为800 m/s,TDOA添加10 μs均方根的时延误差。

图5 角度入射定位误差对比图
图5为该射击条件下,3种传感器布阵方式的定位误差等高线对比图,可见:
1)图5(a)为水平H阵列,靶面60%的定位误差在2 cm以内,最大误差约4 cm。
2)图5(b)为垂直H阵列,靶面40%的定位误差在5 cm以内,最大误差在靶面上部超过1 m,解算失效。
图5(c)为混合式阵列,靶面80%的定位误差在4 cm以内,最大误差约8 cm。
对比图4、图5中得出结论:
1)弹丸水平入射时,混合式传感器阵列对于TDOA测量误差的敏感性最低,水平H式次之,垂直H式阵列的时延误差敏感性最高。
2)当弹丸以一定角度入射时,垂直H式阵列的定位误差在靶面上端急剧上升;混合式阵列的误差敏感度逐渐增大,并在靶面底部角落出现激增;而水平H式阵列的定位误差对入射角的影响较弱。
2.3 讨 论
1)水平阵列在全靶面大角度射击时表现最优,缺点在于占地面积较大地形条件要求高,可用于固定式、移动式装甲靶标的精度射击训练;
2)垂直阵列占地面积小,对地形要求低,缺点在于大角度入射时定位误差急剧增加,可用于正面射击的单兵、班组类固定式、升降式显隐靶标的精度射击训练;
3)混合阵列在靶面中心表现良好,缺点是占地面积大,机械本体设计复杂,可用于大型武器定型射击实验以及空对地目标精度射击训练。
因此在开放式靶标设计中,根据几种布阵方式的优缺点,针对不同设计要求如靶标体积,地形限制等,可选择相应阵列方式。
实践中将此3种阵列方式经过微调,用于各兵种合同战术训练基地及基层部队的实弹靶标训练中,对于95枪、高射机枪及各类直瞄火炮的射击结果与本文仿真结果基本一致,有效达到了最佳的射击训练效果,具体数据限于篇幅不再赘述。
3 结束语
文章论述了一种基于开放式靶标的新型建模方式,并提供了该建模方式的数学解算方法,该模型及算法的通用性较强,可用于不同激波传感器阵列方式的检靶系统。文中针对不同的传感器阵列方式进行Matlab仿真,分析多种传感器阵列方式中时延误差对定位误差影响,为开放式靶标系统的设计提供理论依据。
参考文献:
[1]张飞猛,马春茂.对空射击声学靶脱靶量测试系统的精度分析[J].兵工学报,2000(1):23-26.
[2]张飞猛,战延谋,周钢锋,等.声学立靶弹着点测试数学模型与误差分析[J].应用声学,2006,25(4):252-257.
[3]黄克平,应浩,黄婷,等.开放式三维T靶的数学模型建立及其解析算法[J].四川兵工学报,2008,29(5):124-126.
[4]Shock wave triggered target indicating system[P].美国专利(US4261579).
[5]樊长虹,杜立,管文辉,等.风速对声点阵里把系统建模及算法的影响研究[J].应用声学,2015(5):445-450.
[6]Time-difference process and apparatus for scoring supersonicaerialprojectiles[P].美国专利(US20030008265).
[7]孙书学,吕艳新,顾晓辉,等.双三角声学靶信息融合定位模型[J].兵工学报,2008,29(9):1094-1098.
[8]Acoustic counter-sniper system[P].美国专利(US5930202).
[9]童俊杰,孙志平,邓同兵彬,等,基于激波信号的弹丸坐标测量系统研究[J].仪表技术,2015(5):31-34.
[10]于正亮,肖曦.开放式声电定位报靶系统[J].四川兵工学报,2015,36(2):15-17.
[11]闵想.基于TDOA的声学立靶自动报靶方法研究[D].南京:南京理工大学,2013.
[12]高楼,基于传感器立体布阵的激波报靶系统[D].大连:大连理工大学,2014.
[13]冯斌,石秀华.双三角阵声靶测试系统研究[J].应用声学,2012(2):140-144.
[14]杨俊梅,王建华,成龙,等.基于超声传感器的自动报靶系统设计与实现[J].电子技术,2012,39(6):50-52.
[15]柯彪,高跃飞,罗炳华,等.C#与MATLAB混合编程在内弹道设计中的应用[J].弹箭与制导学报,2013,33(5):129-132.
[16]应浩,黄克平.开放式T靶弹丸斜入射风矢量修正模型[J].兵工自动化,2015,34(7):12-14.

