全方位移动康复机器人重心偏移时的轨迹跟踪控制

姜莹

（沈阳化工大学信息工程学院，辽宁沈阳，110142）

0 引言

目前，我国和世界上一些国家一样，正在步入低出生率的老龄化社会[1]。大量医学数据表明，老年人四肢灵活性急剧下降，急性心脑血管疾病和神经系统疾病的发病率明显增高[2]，多数患者伴随偏瘫症状，患心脑血管疾病的人群呈年轻化趋势[3]。交通方面，近年由于交通事故导致的肢体损伤人数在逐年上升，各领域对康复训练的需求明显增加。然而，目前正面临着专业康复医护人员严重短缺和高额的医疗费用等问题。因此，及时研制一种帮助下肢行动不便患者恢复训练用的全方位下肢康复机器人是十分必要的，正确、科学的康复训练对患者肢体运动功能的恢复和提高将起到重要作用。

全方位康复机器人是一个集多种运动、训练模式为一体的复杂过程，本文聚焦重心偏移和患者自身负载变化对非线性全方位康复机器人轨迹跟踪精度的影响。最优控制[4-6]虽然能够对评价指标获取一个最优值，但是设计最优控制器需要被控参数的精确值；PID控制[7]尽管不需要被控参数的精确值，可以通过内部调节获取参数最优值，但是，对象参数一旦发生改变，PID控制器参数就需要被反复调节。因此，对重心发生变化时的康复机器人准确跟踪，那些适用于线性对象的模型参考自适应控制和PID控制已不适用于非线性全方位康复机器人。

本文提出一种高精度新型轨迹跟踪策略，对机器人结构、参数、环境等不确定性因素，尤其针对全方位移动康复机器人重心偏移和负载变化，设计考虑参考路径加速度、速度信息的控制律来补偿系统中的未知时变部分，提高跟踪精度进而获取良好的跟踪性能。本文第一部分针对全方位移动康复机器人重心偏移时进行运动学、动力学分析；第二部分提出解决重心偏移和负载变化的轨迹跟踪方法；第三部分用上述方法对重心偏移和负载变化进行仿真验证；第四部分给出简短的结论。

1 全方位康复机器人的模型结构

1.1 全方位康复机器人

图1 全方位康复机器人及其全向轮

全方位康复机器人及其全向轮结构如图1所示，机构主要特征是由一个四轮驱动的全方位移动底盘和一个支撑平台组成，全向轮可以最大程度真实模拟正常人在平面内任意方向运动的行走特点，支撑平台高度可根据患者身高调节。机器人高度在900~1200mm范围内可调以供不同身高患者使用。机器人质量58kg，为保证训练安全，最大设定速度为0.25m/s。

1.2 考虑重心偏移情况下的数学模型建立

本文康复机器人坐标系设定和模型结构如图2所示。

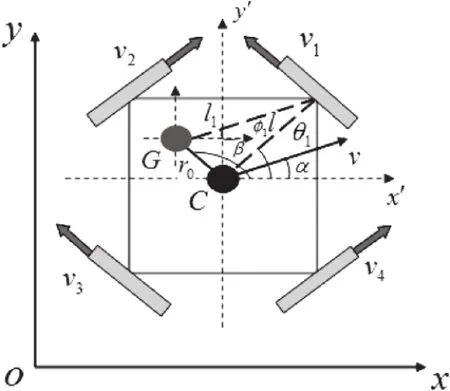
图2 考虑重心的全方位机器人模型结构

图2 中主要参数定义如下：

vi：第i个轮的速度(i = 1 ,2,3,4)；G ：康复机器人的重心；C：康复机器人的中心；li：机器人重心与各轮中心之间的距离(i =1,2,3,4)；θi：机器人各轮与x′轴之间的夹角(i=1,2,3,4)；ϕi：机器人实际重心处测量的各轮位置与x′轴之间的夹角(i = 1 ,2,3,4)；r0：康复机器人重心与中心之间的几何距离；β：r0与x′轴之间的夹角。

机器人几何中心C处的运动学方程描述为：

式（1）、（2）中，xCv 和yCv 表示机器人几何中心C处x、y方向的分解速度，xGv 和yGv 为机器人重心G处x、y方向的分解速度。

重心偏移时全方位康复机器人的动力学模型如下：

式中，M为机器人质量，xa为康复机器人的横向加速度，ya为康复机器人的纵向加速度，θ˙˙为康复机器人的角加速度，1lf、lf2、lf3、lf4分别表示四个全向轮的控制转矩。

为设计重心偏移和负载变化时轨迹跟踪控制器，我们把式（3）转化为矩阵形式：

2 控制器设计

针对模型（9），提出存在正定对称矩阵P、Q，当满足条件0r、β是常数，M m C+ = （C为常数）时，控制器（10）能使系统（9）达到渐进稳定：

3 仿真

3.1 仿真条件设定

直线跟踪路径描述为：

仿真初始条件设定为 xcd(0)=0m，ycd(0)= 0 m，θcd(0) = π2rad，xc(0)= 1 m，yc(0)= 1 m，θc(0) = π3rad ，仿真时间 t = 3 00s，α =−0 .02s−1。

3.2 双闭环PI控制器

下面将本文控制策略与双闭环PI控制器进行对比，双闭环PI控制器由内速度环控制和外位置环控制所组成，两个控制器均执行PI控制，方框图如图3所示。

图3 双闭环PI控制策略方框图

外环保证全方位机器人按照期望轨迹运动，PI控制的位置控制器如式（15）所示：

内环保证速度能够跟踪每个全向轮的参考速度，PI控制的速度控制器如式（16）所示：

3.3 仿真结果

（1）双闭环PI控制器：图4为双闭环PI控制器分别在m = 4 5k g, r0= 0 .2m, a nd β = 2.36rad 重心偏移情况下的线性直线跟踪。

图4 m = 45k g, r 0 = 0.2m, a nd β = 2.36rad 时双闭环PI控制的仿真结果

在图4（a）中，横轴代表时间，纵轴表示x方向位移；在图4（b）中，横轴代表时间，纵轴表示y方向位移；在图4（c）中，横轴表示时间，纵轴表示跟踪的方向角；图4（d）给出全方位康复机器人的路径跟踪效果。点划线代表参考响应，实线代表双闭环PI控制实际响应。从图4可以看出，当荷重变化为 m = 4 5kg产生r0=0.2m , a nd β = 2 .36rad 重心偏移时，前180s内的跟踪误差明显变大，在180s之后才能跟踪期望轨迹。

（2）本文控制器：图5为应用本文控制器在m = 4 5k g, r0= 0 .2m, a nd β = 2 .36rad 重心偏移情况下的直线仿真结果。

图5 m = 45k g, r 0 = 0 .2m, a nd β = 2 .36rad 时本文控制器的仿真结果

图5 （a）-（c）分别表示本文控制器对x方向、y方向和前进方向角的跟踪情况；图5（d）表明全方位康复机器人的路径跟踪情况。由图5可以看出，当重心偏移0r从0.00m 变为0.2m，β从0.00 rad 变为2.36 rad时，应用本文所提出的控制器能够迅速跟踪x 、y 方向和方向角的位置，路径跟踪效果良好，由于控制器中包含了参考路径的加速度、速度信息，从快速性和精度上有效地提高了控制器的跟踪性能。

4 结束语

本文对全方位康复机器人重心偏移情况进行运动学、动力学分析，提出一种按参考轨迹设计控制器的新型控制器设计方法，在保证Lyapunov稳定性的同时，能够对期望路径实现快速、准确的跟踪。最后，对所提出控制器进行细致的仿真研究，表明控制器对存在重心偏移和负载变化的全方位康复机器人轨迹跟踪控制的有效性。

参考文献

[1]郑晓瑛,陈立新.中国人口老龄化特点及政策思考[J].中国全科医学.2006,9(23): 1920-1923.

[2]范晓华,宫艺,刘俊兰.早期康复对脊髓损伤患者步行功能恢复的临床观察[J].中国康复理论与实践.2004,10(7):421-422.

[3]邓志东,程振波.我国助老助残机器人产业与技术发展现状调研[J].机器人技术与应用.2009,2: 20-24.

[4]Peng K, Yan T R, Li H Z. Adaptive admittance control of a robot manipulator under task space constraint.Proceedings of ICRA, Anchorage, AK, 2010.

[5]Tan R P, Wang S Y, Jiang Y L, et al. Adaptive control for omini-directional walker: improvement of dynamic model[C]. Proceeding of the 2011 IEEE International Conference on Mechatronics and Automation. pp. 325-330, 2011.

[6]Tan R P, Wang S Y, Jiang Y L, et al. Motion control of an omini-directional walker using adaptive control method[C]. ICIC Express Letters, vol. 4, No.6(A), pp.2195-2199, 2010.