油水两相流超声测试机理仿真建模

邵一哲，谭超，董峰



油水两相流超声测试机理仿真建模

邵一哲，谭超，董峰

(天津大学 电气自动化与信息工程学院，天津市过程检测与控制重点实验室，天津，300072)

针对油水两相流双连续分散流动条件下流动参数的有效获取问题，采用仿真建模技术，对油水两相流超声测试机理进行研究。通过建立反映实际流动状况的数值仿真模型，讨论超声频率和离散相粒径尺度对超声传播的影响，分析双连续分散流中超声衰减与油相含率之间的关系和超声的作用方式。研究结果表明：所建立的仿真模型可有效描述油水两相流超声测试方法机理。

油水两相流；双连续分散流；超声测试；有限元仿真；传播机理

油水两相流在石油的开采、运输等过程中广泛存在。双连续分散流作为油水两相流流动过程中的一种复杂的流型，常见于低黏度油的油水两相流中。通常有2种：当两相混合流速较高时，为上层油包水下层水包油流型；当两相混合流速较低时，为分层流及混合界面流型。双连续分散流流动状态十分复杂，其参数容易受到温度、压力、管道材质以及连续相流体流动速度的影响[1]。超声波测量方法作为一种非接触的测量方法，其原理主要是基于超声的衰减、反射、折射等作用，通过获得超声多普勒效应、超声渡越时间等特征，实现对多相流流动过程参数，如分相含率和流动速度等进行测量。同时，超声的衍射、绕射作用也广泛应用于对被测物体内部缺陷的无损探测[2]及超声成像[3]等方面。自20世纪80年代以来，已经有诸多学者对超声测量方法进行了大量研究。XU等[4]在管道两侧相对放置1对超声传感器，实现气液两相流中气相浓度额测量，提出脉冲式超声波可以有效抑制驻波对测量结果的影响，并通过检测峰值的方法来提取接收端流体的有效信息。BONNET等[5]采用超声透射的方式，利用平均时间模型计算相含率。SOONG等[6]利用超声透射法，对高压反应釜中的气液固悬浮物特性进行了研究，发现固体颗粒浓度与气相含率相比，影响接受端超声信号幅值，传播时间较小。OHKAWA等[7]利用插入深度可调的超声传感器，对浆态鼓泡床反应器内分散相的轴向及径向相含率分布分别进行了测量，并对分布特性进行了分析。ZHENG等[8]将超声传感器运用在气液固三相流中，发现气液两相流中气泡空隙率与声波传播时间波动性存在关系，液固两相流中固体颗粒会引起超声信号幅值明显变化。CARVALHO等[9]采用单发多收的超声传感器结构，探讨了超声波在气液两相流不同流型中的透射、反射与散射现象，并讨论了气液两相流流动结构及孔隙率对超声衰减及传播时间的影响。在油水两相流中，由于两相流体的流动形态复杂多变，分散相液滴大小和位置也存在很大差别，而超声波的传播作用又受到分散相液滴大小和位置的影响，因此，研究油水两相流中液滴粒径分布，对建立超声作用机理模型有重要意义。针对液滴粒径分布的问题，国内外学者对液滴的聚合和破裂形成等进行了大量研究。SHINNAR[10]发现液滴的聚合与破裂均发生在湍流惯性区。TSOURIS等[11]研究得到液滴之间发生聚合，应存在最小接触时间，而且只有当液滴直径小于最小液滴直径时，液滴间的薄膜才会变得足够薄而破裂。PACEK等[12]指出液滴的聚合取决于其碰撞率与聚合效率，同时根据不同的研究对象，提出了各种描述液滴平均粒径的方法，例如算术平均粒径、面积平均粒径、体积平均粒径以及Sauter平均粒径。WARD等[13]用照相技术获得了垂直向下的油水分散流的Sauter平均粒径，其值随着分散相体积分数的增加而增大，随着速度的加快先增大后减小。而SIMMONS等[14]通过研究得到：随着混合物速度加快，Sauter平均粒径逐渐减小。AL-WAHAIBI等[15]研究了油水双重连续流动中混合物速度对液滴粒径的影响。采用超声波技术进行油水两相流的测量，具有非侵入性、不干扰流体流动等优点，对于油水界面有较敏感的感应能力。为明确超声波在双连续分散流油水两相流中的传播衰减机理，实现流动参数的有效获取，本文作者利用有限元建模方法，建立反映实际流动状况的数值仿真模型，讨论超声工作频率和粒径分布对超声传播的影响，分析双连续分散流中超声的作用方式和超声衰减与油相含率之间的关系，并通过开展实验验证，描述油水两相流超声测试方法的 机理。

1 超声衰减法测量原理

超声衰减测量是基于油水两相流的声学特性不同，实现流动过程测量的一种方法，测量原理如图1所示。超声波发射端发出一定频率和强度的超声波，在油水两相流中穿过，经过油水两相的吸收、反射和散射等衰减机制后，到达超声波信号接收端[16]。由于油相和水相的超声吸收系数不同，当油相含率不同时，超声的衰减系数也就不同，超声衰减系数定义为

式中：1为发射端传感器发射出的平均压强；2为接收端传感器的接收到的平均压强。

当超声波在油水两相流中传播时，除了受到油水两相的吸收、反射和散射等作用的影响，受超声传播途径上以障碍物形式存在的离散相尺度和超声发射频率或在流体中波长的影响外，还会发生波的绕射现象，如图2所示[17]。图中，障碍物后声影截面不变的距离为1，近似为

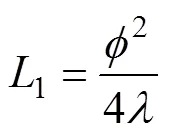
式中：为障碍物粒径，即流体中离散相的直径；为超声波长。

在距离1之后，声束将按角度绕射，根据超声衍射的基本理论推导得到：

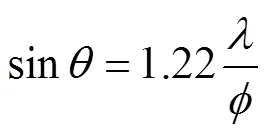
图2 超声传播的绕射现象

当障碍物后的声影截面面积为0时，超声恢复为正常向前传播，则绕射距离2可以表示为

由式(2)~(4)可知：油水两相流中离散相粒径与超声发射频率或在流体中波长的比值影响超声衍射声影长度以及声波绕射角度。因此，采用超声衰减法进行油水两相流测量时，为明确超声衰减的测试机理，需对超声波的传播作用方式与离散相粒径、超声发射频率或在流体中波长的关系进行研究和分析。

2 油水两相流中超声波传播的影响因素

2.1 超声频率对超声传播的影响

为了探究不同超声频率对超声在油水两相流中传播方式的影响，利用COMSOL多物理场耦合仿真软件建立被测场二维几何剖分模型，在管道中利用粒径为2 mm的圆形模拟油泡，均匀分布在连续水相中，仿真模型如图3所示。设定管道内径为50 mm，采用自由剖分三角形划分网格。发射端采用结构−声耦合方式，接收端用二维截线接收衰减后的信号。主要仿真参数设置如下：温度为293.15 K，水的密度 1 000 kg/m3，水中声速为1 500 m/s；油的密度为 850 kg/m3，油中声速为1 324 m/s。

由于超声的波长=/，超声在水相中的传播速度取1 500 m/s，则超声频率与超声波长对应关系以及超声波长与油泡粒径关系如表1所示。

固定油泡个数，在同一油相含率下，改变超声发射频率，得到不同超声波长与油泡粒径关系下的超声在水包油流型中的传播过程仿真结果如图4所示。

图3 油泡均匀分布的油水两相流模型

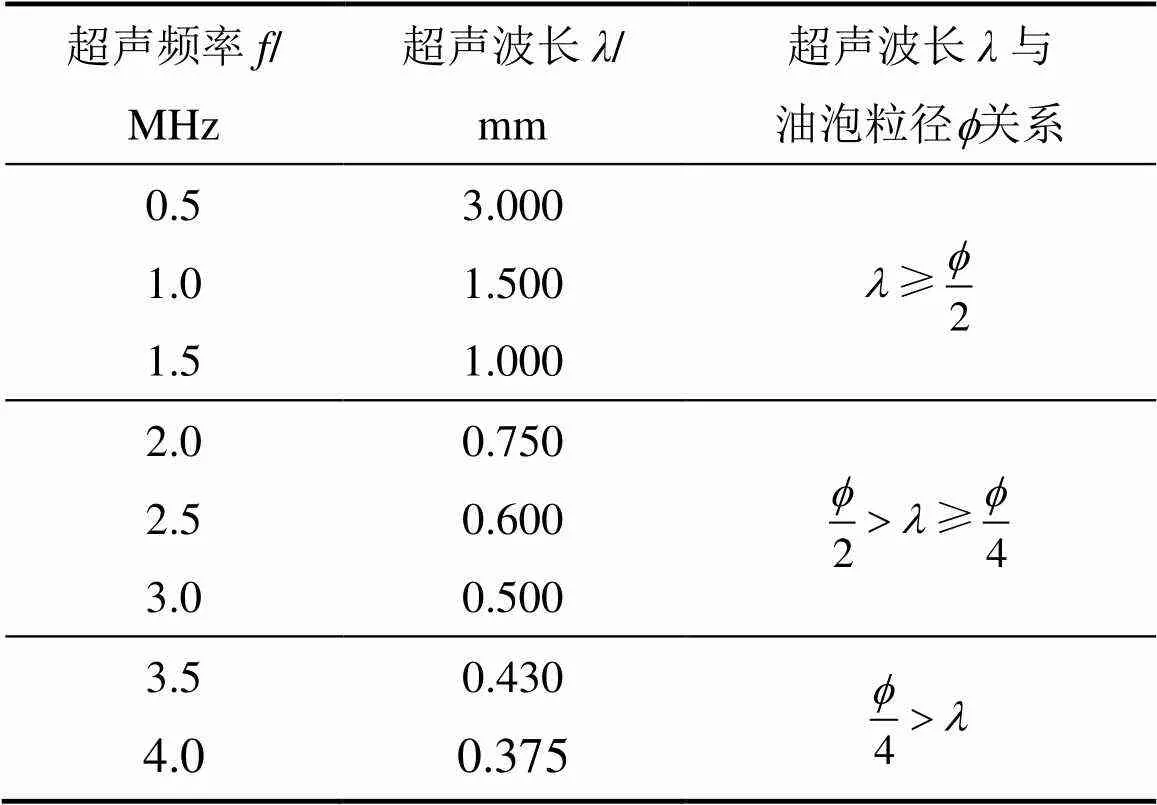
表1 超声频率与波长的对应关系

图4 不同超声频率f的声压分布

2.2 离散相粒径尺度对超声传播的影响

在离散相粒径对超声传播的影响的建模分析中，选定超声发射频率为1 MHz，超声波长为1.5 mm。在超声主传播通道上设计垂直均匀分布的同粒径圆形代表油泡，连续相设置为水。通过改变粒径尺度分别取为0.5，1.0和2.0 mm，来进行不同粒径对超声传播作用方式的影响探究，得到仿真结果如图5所示。根据式(1)得到超声衰减系数随油泡粒径变化如图6 所示。

图5(a)中，障碍物油泡粒径小于超声波长的1/2时，油泡对超声的主要作用体现为衍射作用，超声完全绕过障碍物继续向前传播，离散油泡对超声传播途径几乎没有影响，衰减程度也较小。图5(b)和(c)中，当障碍物粒径大于或等于超声波长的1/2时，油泡对超声的主要作用体现为多次回声反射，少量声波在油泡边缘绕射传播过去，且随着粒径的增大，能绕射过油泡的超声波越少。从图5(c)中的局部放大图像中可观察到：在离散油泡之间，声波经过多次回声反射，中间通路基本呈直线式，只有少量的声波在油泡上边缘发生绕射，将粒径2 mm代入式(2)~(4)，可得出绕射角度约为66°，绕射距离2约为1.11 mm，即在油泡内部形成绕射声影。

从图6可以得到：随着油泡粒径增大，超声衰减系数单调增加。一方面，由于油相含率随着粒径增大而增加，导致对超声传播的衰减作用增强；另一方面，由于油泡粒径的增大，对超声波的衍射和反射作用加强，也会导致超声衰减系数增大。

由于超声频率和离散相粒径对超声在油水两相流中的传播方式均有一定程度的影响，在具体针对某种流型进行超声传播方式及衰减特性研究时，应当选用适合的超声频率，并且建立符合该流型实际流动过程中粒径分布的仿真模型。

f/mm：(a) 0.5；(b) 1.0；(c)2.0

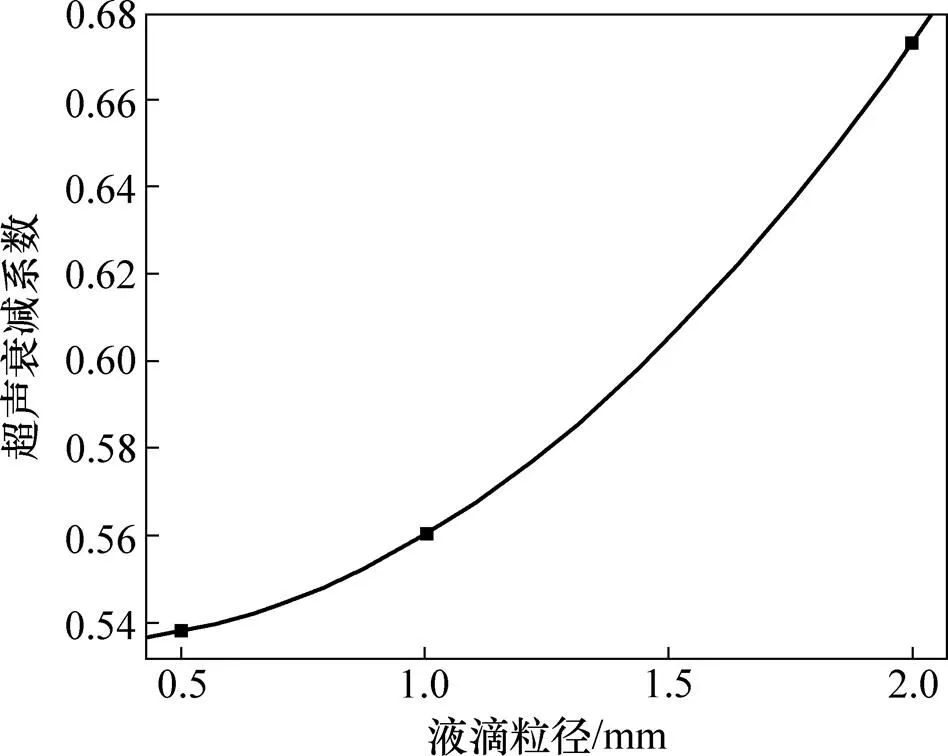
图6 油泡粒径对超声衰减系数的影响

双连续分散流作为一种常见的油水两相流，具体分为2种流型：当两相混合流速较高时，为上层油包水下层水包油流型；当两相混合流速较低时，为分层流及混合界面流型。因此，需要分别针对2种流型具体讨论超声在其中的传播方式及衰减特性。

3 油水两相双连续分散流中超声传播方式及衰减特性

3.1 上层油包水下层水包油建模与结果分析

根据LOVICK等[18]对于水平管双连续分散流中的粒径以及垂直分布的研究结果，即液滴距离油水界面距离越远、粒径越小的粒径分布规律，建立上层油包水下层水包油流型的仿真模型。模型中，在内径为50 mm的管道外面设计了一层直径为80 mm的玻璃层和一层直径为90 mm空气模拟层，管道内部用贝氏多线段将水和油分界，形成界面。该流型下离散相颗粒分散较充分，充满整个管道，根据粒径分布规律设计了不同粒径的油泡，模拟油相含率范围为45%~60%。以油相含率为45%，50%和60%为例，得到超声在油水两相流中传播的声压分布如图7所示。通过超声发射接收端采集声压，结合式(1)得到超声衰减与油相含率的变化关系如图8所示。

由图7可见：超声的散射方向呈有规律的多边形辐射状，流体内部超声传播方式十分复杂。从图8可得：随着油相含率增加，超声衰减系数呈先增大后减小的趋势。在一定油相含率范围内，随着油相含率增加，由于油相的衰减系数大于水相的衰减系数，超声的衰减系数增加；超出一定范围后，随着油泡数量增加，流体内混乱程度增大，油水相界面增多，超声在传播过程中的折射绕射作用增强，导致接收端信号增强，超声衰减系数减小。

3.2 分层流及混合界面的建模与结果分析

根据天津大学油气水多相流实验装置上进行的水平油水两相流流动实验，利用高速摄像技术得到的层流流动截面图像，建立分层流及混合界面流型油水两相流的仿真模型。此流型下离散相颗粒分布主要集中在油水分界面两侧，随着油相含率的增加，油水分层界面下降，同时离散相分布情况也有明显改变。所建立的仿真模型中，用贝氏多线段将水和油分界，形成界面，根据截面图像设计不同粒径的油泡，模拟油相含率范围为20%~55%。以油相含率为23%，44%和52%为例，得到超声在油水两相流中传播的声压分布如图9所示，超声衰减与油相含率的变化关系如图10所示。

由图9可见：随着油相含率增加，油水界面较超声发射传感器位置下降，伴有超声的多重反射作用以及介质对超声的吸收作用，辐射状折射作用减弱，但是散射方向依旧是有规律的。从图10可知：超声衰减系数随着油相含率的增加，呈先增大后减小再增大的波动趋势。这是因为当油相含率介于20%~35%范围内时，油水两相流动速度较慢，油水混合界面波动较小，有少量水泡油泡分散在油水界面两侧，此时超声主导传播模式是反射、折射作用；随着油相含率的增加，超声衰减系数呈增大趋势；当油相含率介于35%~45%范围时，油相流量增加致使流体流动速度增大，分散的泡被击碎为更小粒径的分散相，混合界面范围增大，混乱程度增加，有部分超声衍射作用发生，随着油相含率的增加，超声衰减系数减小；当油相含率大于45%后，油水两相流量持平，相对速度变小，极小粒径的分散相很容易破裂，导致油水分界面相对超声发射传感器位置下移，由于上层连续相为油相，对超声的吸收衰减作用很大，所以，超声衰减系数随着油相含率的增大而大幅度增大。

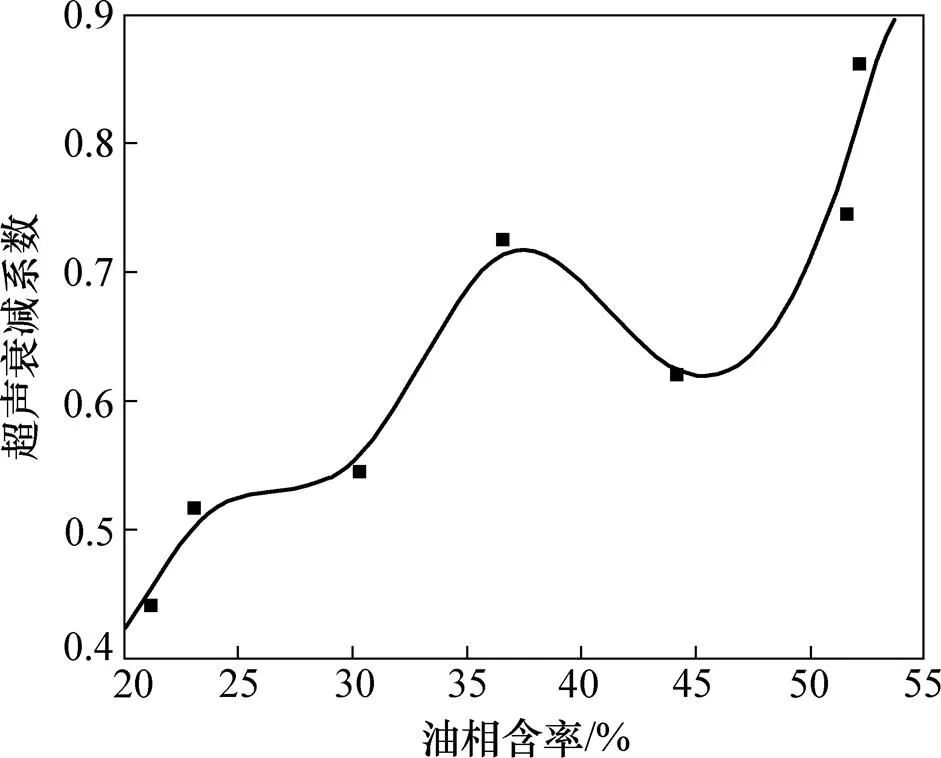
图10 分层流及混合界面流型超声衰减系数与油相含率之间的关系

4 实验验证

为了对油水两相流中超声衰减特性的仿真分析结果进行验证，利用天津大学油气水多相流实验装置进行油水两相流动过程超声测试实验[19]。实验中，选取超声发射频率为1 MHz，采用的超声传感器直径为 6 mm，激励电压为10 V；测试管道内径为50 mm，油相采用工业白油，密度为841 kg/m3；水相为自来水，密度为998 kg/m3。实验时采用的所测试的油相含率范围为45%~75%，实验测试所得数据如表2所示，超声衰减系数随油相含率变化的结果如图11所示。

通过对比实验测试结果以及仿真得到的结果，对于上层油包水下层水包油流型中超声衰减随着油相含率的变化关系，图8中的仿真结果与图11(a)中的实验结果较吻合；而对于分层流及混合界面流型，由于实际实验流量配比等问题的限制，实验仅得到35%~55%范围内的超声衰减信息，在这一范围内，超声衰减随着油相含率的变化关系(图11(b))与图10中的仿真结果也能在趋势上较好地吻合。所以，基于粒径分布的仿真模型在一定程度上能较好地反映实际流体流动的状态，通过仿真能更加直观地观察和分析超声在双连续分散流中的传播衰减特性。

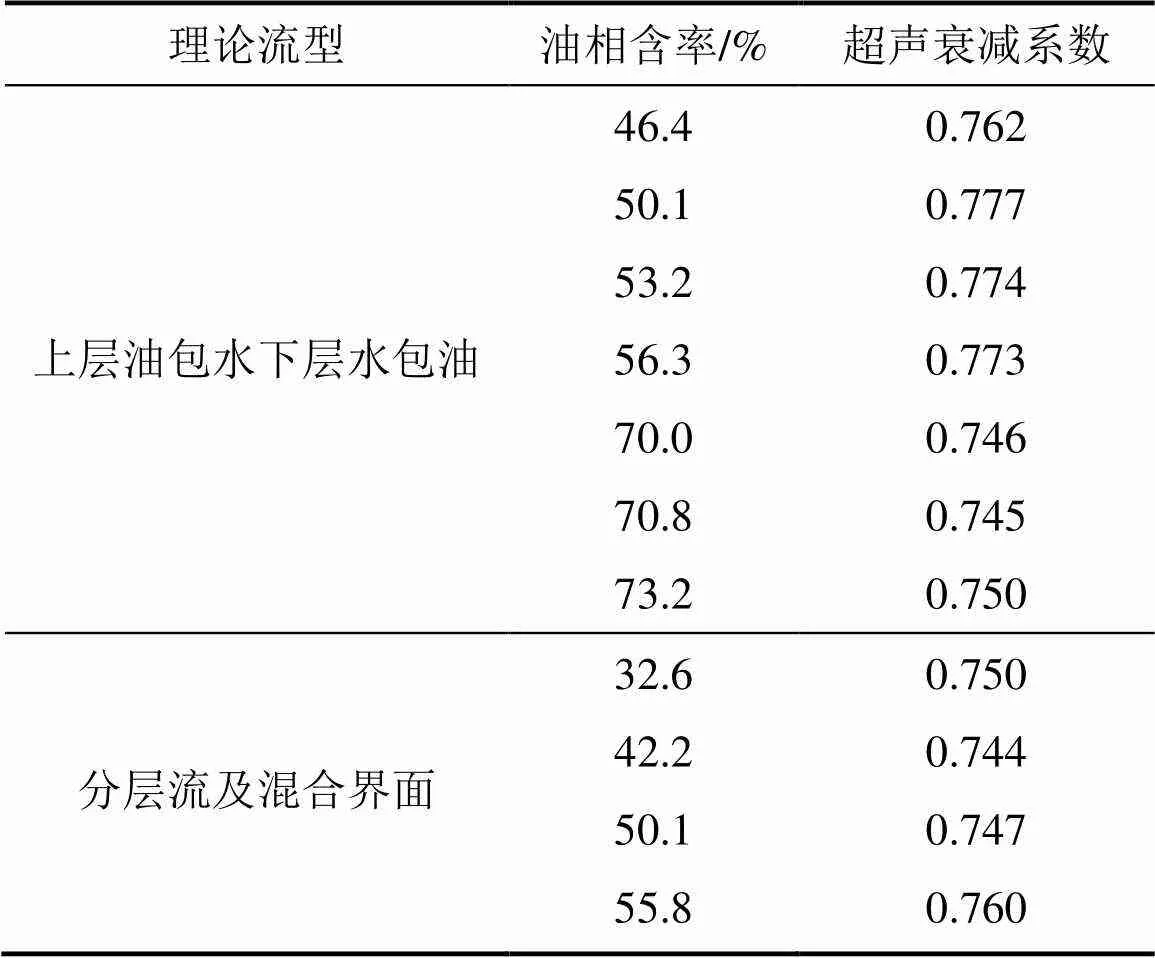
表2 实验测试数据

图11 实验得到的超声衰减系数变化

5 结论

1) 针对油水两相流流动参数的有效获取问题，为明确油水两相流中超声波传播的影响因素和典型油水两相流中超声传播方式及衰减特性等问题，通过对油水两相流超声测试机理进行分析，采用数值仿真建模技术，建立水为连续相的油水两相均匀分布仿真模型；并根据实际生产中较多存在的油水两相双连续分散流动状态，建立上层油包水下层水包油、分层流及混合界面的仿真模型。

2) 在建立的水为连续相的油水两相均匀分布仿真模型的基础上，通过对超声工作频率和分散相油泡粒径尺度对超声传播影响的分析，得到了超声测试的有效工作频率与分散相油泡粒径的关系。随着油泡粒径增大，超声衰减系数单调增加。

[1] ANGELI P, HEWITT G F. Drop size distributions in horizontal oil-water dispersed flows[J]. Chemical Engineering Science, 2000, 55(16): 3133−3143.

[2] 郑晖, 胡斌, 林树青, 等. 国外TOFD检测标准分析和比较[J]. 无损检测, 2007, 29(3): 150−154.ZHENG Hui, HU Bin, LIN Shuqing, et al. Analysis and comparison of TOFD detection standard abroad[J]. Non-destructive Testing, 2007, 29(3): 150−154.

[3] 倪文磊. 超声CT理论与方法综述[J]. CT理论与应用研究, 2004, 13(3): 50−55. NI Wenwei. Ultrasound CT theory and methods[J]. Computerized Tomography Theory and Applications, 2004, 13(3): 50−55.

[4] XU L A, LEONARD D, GREEN R G. A pulsed ultrasound transducer system for two component flow[J]. Journal of Physics E: Scientific Instruments, 1985, 18(7): 609−613.

[5] BONNET J C, TAVLARIDES L L. Ultrasonic technique for dispersed-phase holdup measurements[J]. Industrial & Engineering Chemistry Research, 1987, 26(4): 811−815.

[6] SOONG Y, GAMWO I K, BLACKWELL A G, et al. Ultrasonic characterization of slurries in an autoclave reactor at elevated temperature[J]. Industrial and Engineering Chemistry Research, 1996, 35(6): 1807−1812.

[7] OHKAWA W M, MAEZAWA A, UCHIDA S. Flow structure and phase distributions in a slurry bubble column[J]. Chemical Engineering Science, 1997, 52(21/22): 3941−3947.

[8] ZHENG Ying, ZHANG Qikai. Simultaneous measurement of gas and solid holdups in multiphase systems using ultrasonic technique[J]. Chemical Engineering Science, 2004, 59(17): 3505−3514.

[9] CARVALHO R D M, VENTURINI O J, TANAHASHI E I, et al. Application of the ultrasonic technique and high-speed film for the study of the structure of air-water bubbly flows[J]. Experimental Thermal and Fluid Science, 2009, 33(7): 1065−1086.

[10] SHINNAR R. On the behaviour of liquid dispersions in mixing vessels[J]. Journal of Fluid Mechanics, 1961, 10(2): 259−275.

[11] TSOURIS C, NORATO M A, TAVLARIDES L L. A pulse-echo ultrasonic probe for local volume fraction measurements in liquid-liquid dispersions[J]. Industry & Engineering Chemistry Research, 1995, 34(9): 3154−3158.

[12] PACEK A W, NIENOW A W. A problem for the description of turbulent dispersed liquid-liquid systems[J]. International Journal of Multiphase Flow, 1995, 21(2): 323−328.

[13] WARD J P, KNUDSEN J G. Turbulent flow of unstable liquid-liquid dispersions: Drop sizes and velocity distributions[J]. AIChE Journal, 1967, 13(2): 356−365.

[14] SIMMONS M J H, ZAIDI S H, AZZOPARDI B J. Comparison of laser-based drop-size measurement techniques and their application to dispersed liquid-liquid pipe flow[J]. Optical Engineering, 2000, 39(39): 505−509.

[15] AL-WAHAIBI T, ANGELI P. Droplet size and velocity in dual continuous horizontal oil–water flows[J]. Chemical Engineering Research and Design, 2008, 86(1): 83−93.

[16] 苏茜, 董峰. 油水两相流超声波衰减测试方法[J]. 中南大学学报(自然科学版), 2016, 47(2): 647−653. SU Qian, DONG Feng. Ultrasound attenuation measurement of oil-water two-phase flow[J]. Journal of Central South University (Science and Technology), 2016, 47(2): 647−653.

[17] 宋天民. 超声检测[M].北京:中国石化出版社, 2012: 56−59.SONG Tianmin. Ultrasonic measurement[M]. Beijing: China Petrochemical Chemical Industry Press, 2012: 56−59.

[18] LOVICK J, ANGELI P. Droplet size and velocity profiles in liquid-liquid horizontal flows[J]. Chemical Engineering Science, 2004, 59(15): 3105−3115.

[19] TAN Chao, WANG Nana, DONG Feng. Oil–water two-phase flow pattern analysis with ERT based measurement and multivariate maximum Lyapunov exponent[J]. Journal of Central South University, 2016, 23(1): 240−248.

(编辑 杨幼平)

Modeling of ultrasonic measurement mechanism in oil-water two-phase flow

SHAO Yizhe, TAN Chao, DONG Feng

(Tianjin Key Laboratory of Process Measurement and Control,School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China)

To get effective informations of the flow parameters in the dual continuous oil-water two-phase flow, the ultrasonic testing mechanism of oil-water two-phase flow was studied by simulation modeling technique.By establishing a numerical simulation model which could reflect the actual flow condition, the influence of ultrasonic frequency and particle size on the ultrasonic propagation was discussed. The relationship between ultrasonic attenuation and oil phase content was analyzed and the mode of ultrasonic action was also analyzed. The results show that the simulation model can effectively describe the mechanism of ultrasonic testing in oil-water two-phase flow.

oil-water two-phase flow; dual continuous flow; ultrasonic measurement; finite element simulation; propagation mechanism

O359，TP271+.3

A

1672−7207(2018)04−0987−08

10.11817/j.issn.1672−7207.2018.04.029

2017−04−29；

2017−06−22

国家自然科学基金资助项目(61227006，61473206)；天津市科技创新平台建设计划项目(16PTSYJC00060) (Projects(61227006, 61473206) supported by the National Natural Science Foundation of China; Project(16PTSYJC00060) supported by the Science and Technology Innovation Plan of Tianjin City)

董峰，博士，教授，从事多相流测试技术与信息处理研究；E-mail：fdong@tju.edu.cn