基于3-D步行序列的双足机器人步态规划及实验研究

陈建芳，丁加涛，肖晓晖



基于3-D步行序列的双足机器人步态规划及实验研究

陈建芳，丁加涛，肖晓晖

(武汉大学 动力与机械学院，湖北 武汉，430072)

为了提高双足步行机器人对真实环境的适应能力，提出1种基于3-D步行序列的步态规划方法，模仿人类行走行为并考虑地面高度的变化。首先定义考虑足部踝关节旋转运动和机器人质心(COM)竖直高度变化的3-D步行序列。其次，在单足相阶段(SSP)，基于运动最优控制(OC)理论和线性倒立摆模型 (LIMP)，求解零力矩点轨迹；采用5次多项式插值，生成双足相阶段(DSP)的零力矩点轨迹，并且实现质心竖直高度变化。基于足部的运动参数，使用分段连续3次Hermite插值得到足部运动轨迹。然后，通过牛顿−拉斐逊迭代法求解关节角度解。最后，基于NAO机器人样机进行平地和倾斜地面行走的动力学仿真和样机实验。研究结果表明：本文规划方法可行，且机器人行走平稳；在平面和斜坡2种地面工况的样机实验中，足底接触力的波动幅度比相应的仿真结果分别减少37.01%和59.94%，髋关节力矩波动幅度分别减少69.13%和62.75%。

3-D步行序列；双足机器人；步态规划；斜坡

近年来，提高双足步行机器人对真实环境的适应能力成为研究热点。目前，针对双足步行机器人的步态规划理论基础，KAJITA等[1]提出了一个基于三维线性倒立摆模型的经典步态生成理论；DASGUPTA等[2]采用基于零力矩点(ZMP)的方法进行了步态规划研究；FUJIMOTO等[3]通过设计摆动足和双足步行机器人质心轨迹求解步态，将双足步行机器人的质心看作是线性倒立摆，摆动腿末端的运动轨迹用连接2 个采样时间的落地点的平滑函数来表示；王志良等[4]进行了基于ZMP判据的机器人步行模式与步态规划研究。然而，以上研究均针对平地行走的情况。针对机器人斜坡行走，HUANG等[5]在平地小车−桌子模型的基础上提出1种斜面小车−桌子模型，即给定零力矩点轨迹，利用预观控制得到质心轨迹，从而实现斜面的上、下坡；ZHOU等[6]根据斜坡运动的约束关系建立数学模型, 找到机器人斜坡运动的最优解, 从而实现机器人斜坡运动；NAGASUE等[7]基于理想零力矩点并利用最近邻接法确定出最优的机器人斜坡运动的关节角度；ALI等[8]提出2种斜面步态规划方法：一是采用基于位置和方向的逆运动学法，保持质心高度不变，首先对平地步态规划，然后将该规划应用到斜坡地面上；二是提出双线性倒立摆的方法，采用牛顿−拉斐逊(Newton Raphson)算法对矢量平面和侧向平面的步态进行规划以确保同步，该方法可保证质心高度可 变[9]。此外，张文[10]建立了仿人机器人斜面行走的非正交解耦模型和双腿长线性倒立摆模型，提出了机器人斜面行走通用步态规划方法；杨璟[11]推导了斜面步行的桌子−小车模型，实现了机器人在斜面以0.5 km/h的速度稳定步行；毕盛等[12]设计了由步长、步行周期等参数控制的斜坡运动模式，根据倒立摆原理模型对斜坡步态过程中髋关节和踝关节的轨迹规划，进而实现斜坡运动的步态规划；张克等[13]利用小波神经网络自学习的方法，确定机器人斜坡运动的步态。这些方法能够实现质心高度的竖直方向变化，但是需要单独推导斜坡行走的模型。本文作者基于已有的步态规划理论基础以及本课题组已有成果[14]，提出1种基于3-D步行序列的步态规划方法，模仿人类行走行为并考虑地面高度的变化。定义考虑足部踝关节旋转运动和机器人质心竖直高度变化的3-D步行序列，然后，基于NAO机器人样机进行平地和倾斜地面行走的动力学仿真和样机实验。

1 3-D步行序列参数规划方法

考虑在双足相阶段的质心运动以及摆动脚的旋转，本文提出1种实时步态发生器。在规划零力矩点和质心轨迹之前，首先定义3-D步行序列参数模型(简称WS模型)。单足相阶段的零力矩点和质心轨迹可以看作是基于3D−LIPM的最优控制问题。根据最优控制理论，求解出单足相期间的零力矩点轨迹。通过调试单足相质心的初始和终止位置，可以保证在步长和步宽变化(即相邻周期步宽和步长不同)的情况下，使单足相的零力矩点位移为0 mm。为了保证双足相和单足相期间的位置、速度和加速度的连续性，采用五次多项式插值法生成双足相阶段的零力矩点轨迹。然后用桌子−小车模型数值求解[15]得到连续的质心轨迹，用分段连续的3次Hermite插值得到足部平移和旋转轨迹。

1.1 3-D步行序列参数

与人的步态类似，双足步行机器人的步态可以分为几个阶段，如图1所示。一个完整的步行状态包括2个步行周期(左右脚对称)，每个周期包含单足相和双足相。其中，单足相分为起步、步行和止步3个阶段。

图2所示为参数step的定义。其中：左—前坐标分别表示行走方向，并且与世界坐标系(机器人行走绝对原点)和足部支撑坐标系(局部坐标系)一致；和分别为步长和步宽；上标表示第个支撑周期；为质心前向位移；为侧向位移；(ini,ini)和(end,end)分别为第个周期单足相期间质心的初始和终止状态；pmax， pmin，pmax和pmin分别为局部坐标系原点相对于足部支撑四边形的距离，即零力矩点稳定域度。图3所示为单足相阶段参数foot的定义。其中：COM为质心位置；c为单足向期间质心和地面的固定高度；1为起步阶段最大俯仰角；2为止步阶段最大俯仰角；1为起步阶段时间；2为止步阶段时间；g为两足部之间的垂直高度变化。各参数定义如下：

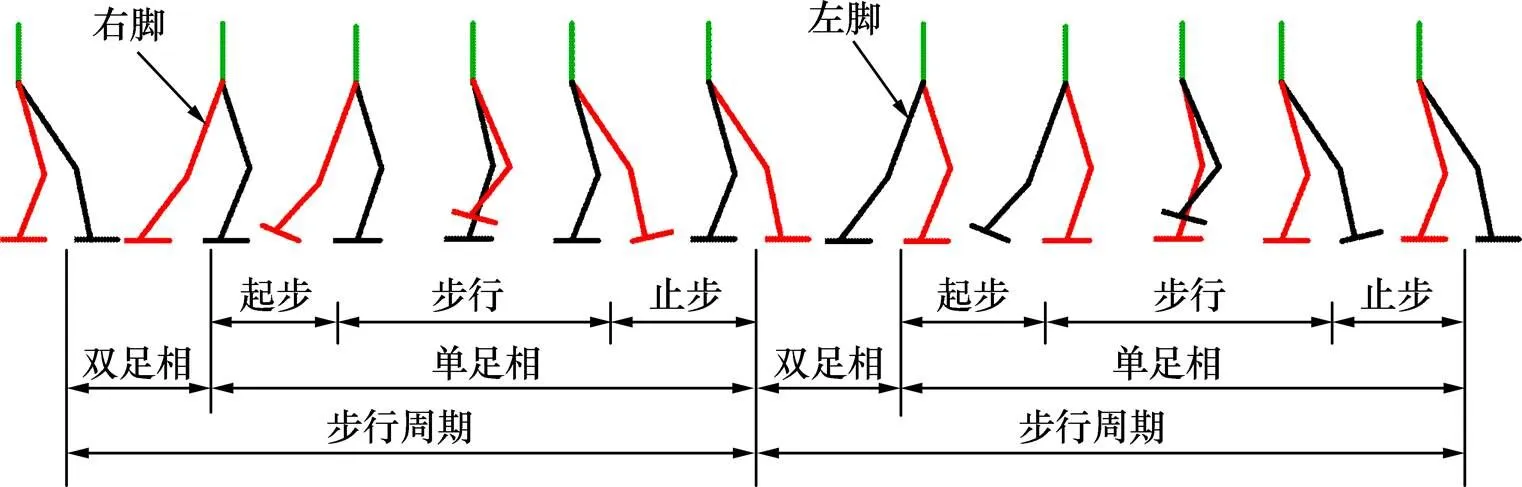
图1 双足步行周期示意图

图2 参数Sstep的定义

图3 单足相阶段参数Sfoot的定义

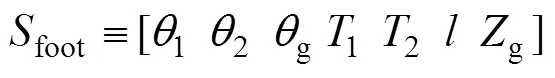
式中：step为步行周期中双足相的状态参数(见图2)；foot为步行周期中单足相的状态参数(见图3)；s为单足相时间；d为双足相时间；g为地面倾角；为摆动腿的最大离地高度；g为两足部之间的垂直高度变化。

1.2 步态规划

1.2.1 单足相阶段的ZMP轨迹生成

本文采用三维线性倒立模型(3D−LIPM)求解单足相阶段的ZMP轨迹[1]。假设机器人的身体质量都集中于1个点，在垂直方向没有运动。通过3D−LIPM 分别得到零力矩点和质心的位移表达公式：

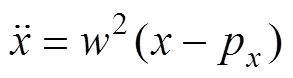
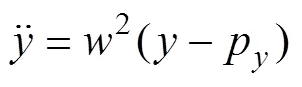
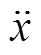
在时间s内，质心从初始状态转移到终止状态。为获得最高稳定性，单足相期间零力矩点位移始终为0 mm。

1.2.2 双足相阶段的零力矩点轨迹生成

考虑到位置、速度和加速度的连续性，采用五次多项式插值得到零力矩点轨迹：

第个步行周期的双足相阶段的边界条件为

1.2.3 双足相阶段的质心高度变化

在双足相阶段机器人的质心垂直运动可以通过五次多项式插值求得。质心垂直运动轨迹为

由于在单足相期间的质心垂直方向运动为0，即c是常数，故双足相阶段的质心垂直运动的边界条件为

1.2.4 足部踝关节轨迹生成

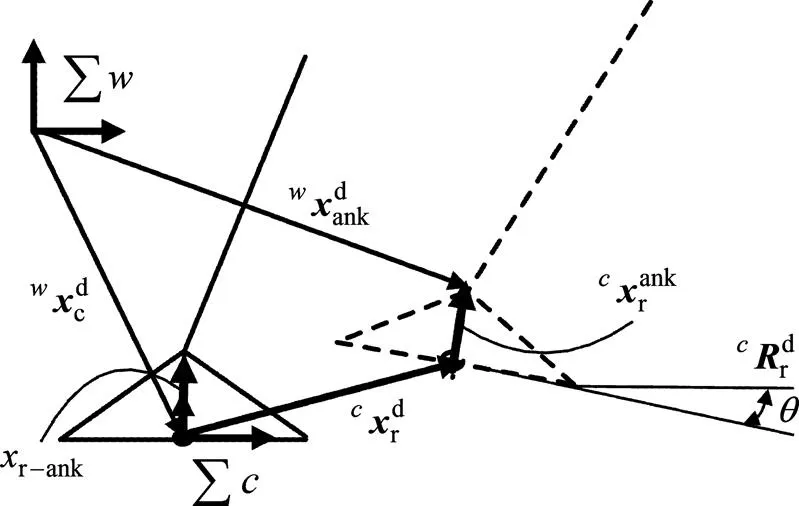
图4 摆动脚的坐标系

2 辅助控制器

虽然上述的步态规划方法能够使机器人在平地上稳定的步行，当机器人受到地面不平等扰动时，仍然会失去平衡，因此，必须要通过传感器的反馈控制使机器人维持平衡。图5所示为双足机器人步行控制器的结构。由图5可知步行器结构分为3层：最上层，双足机器人利用3-D步行序列的步态规划方法预先生成离线步态数据；第2层，传感器反馈控制器根据安装在机器人上身的陀螺仪，实时修正所规划的步态(其中Δb为修正骨宽关节角度)，保证机器人步行的稳定性；第3层，双足机器人的关节伺服控制器把反馈控制器修正后的步态数据发送到关节伺服控制器当中，以控制各关节角位置。

图5 双足机器人步行控制器的整体结构

2.1 上身姿态控制

双足机器人在行走过程中，一方面，希望像人那样保持上身的直立状态；另一方面，当机器人行走在不平整地面或受到扰动时，上身会发生倾斜，如果上身不及时调整姿态，机器人很容易失稳摔倒。纠正上身姿态最有效的手段是控制支撑腿髋关节，因为这个关节直接影响机器人上身的姿态。利用安装在上身的陀螺仪，当机器人检测出姿态发生偏移时，上身姿态控制被激活，然后根据步态生成器所定义的步行阶段来修正当前的支撑腿的髋关节，其修正量可用下式 表示：

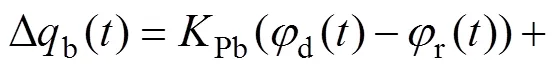
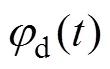
2.2 关节角度跟踪控制

双足机器人的关节伺服控制器把反馈控制器修正后的步态数据发送到关节伺服控制器中，以控制各关节角度。其修正量可用下式表示：

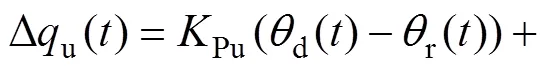
3 仿真与实验

以NAO机器人为对象进行仿真与试验，其腿部参数如表1所示。假设机器人前向行走为轴，左侧为轴，垂直向上为轴。

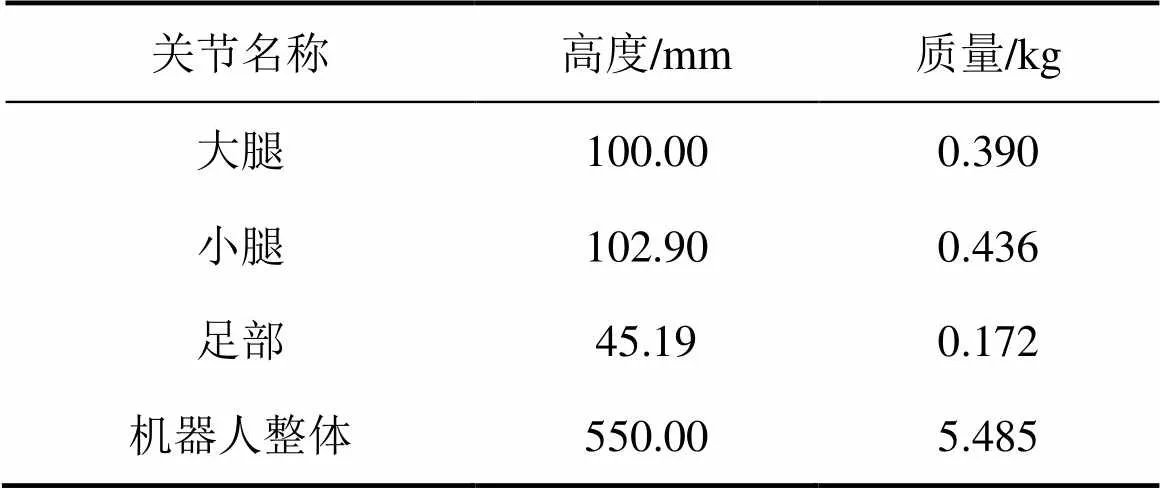
表1 NAO机器人腿部参数

在三维建模软件SOLIDWORKS中建立平地及倾角为5°的斜坡地面模型。2种工况下步态规划参数如表2所示。

3.1 ADAMS仿真实验

将平地和斜坡地面模型导入机械系统动力学自动分析软件(ADAMS)中，设置地面为木质材料。为了减少结构约束，将NAO机器人的上肢简化为1个质量块，如图6所示。然后，利用ADAMS软件中的CUBSPL函数将规划得到的参考角度数据进行拟合。在仿真实验中，机器人可以实现在平地上前进−后退和斜坡上稳定行走。在2种工况下，仿真实验得到的机器人质心轨迹，零力矩点轨迹以及膝关节力矩和足底作用力分别如图7~8所示。其中：和分别表示世界坐标系下和的位移。

由图7可知：在斜坡工况下，仿真实验得到的零力矩点轨迹与规划的轨迹基本一致，其中的不光滑部分曲线，是由于在=400 mm以后，机器人开始上坡步行，地面与足部之间有冲击；在斜坡工况下，仿真的质心轨迹较为平滑且与规划轨迹一致。故仿真实验的结果可信。

表2 2种工况下步态规划参数

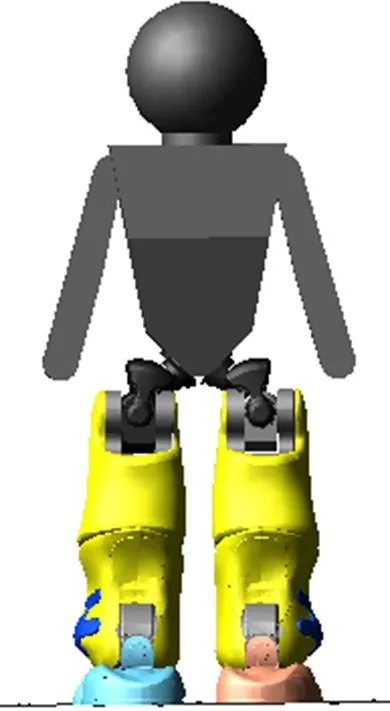
图6 仿真机器人模型

由图8可知：在仿真实验中，膝关节力矩在平地工况下最大达到3.677 N·m，斜坡工况下最大力矩为5.515 N·m，而关节电机允许的最大转矩为8.897 N·m，故满足要求。仿真实验中，足底作用力均在50.0 N左右，这与NAO机器人整体重力54.8 N相符，其中的峰值部分可能是足底与地面接触冲击引起。在平地工况下，足底最大冲击接触力达到89.14 N；在斜坡工况下，足底最大冲击接触力达到102.50 N。

3.2 NAO机器人实验

仿真结束后，以NAO机器人为样机进行实验，NAO样机如图9所示。实验中，利用木板搭建平地和倾角为5°的斜坡2种地面平台。实验中机器人可以实现稳定的平地步行和斜坡步行，采集到的关节电机电流及足底力传感器参数如图10~11所示。

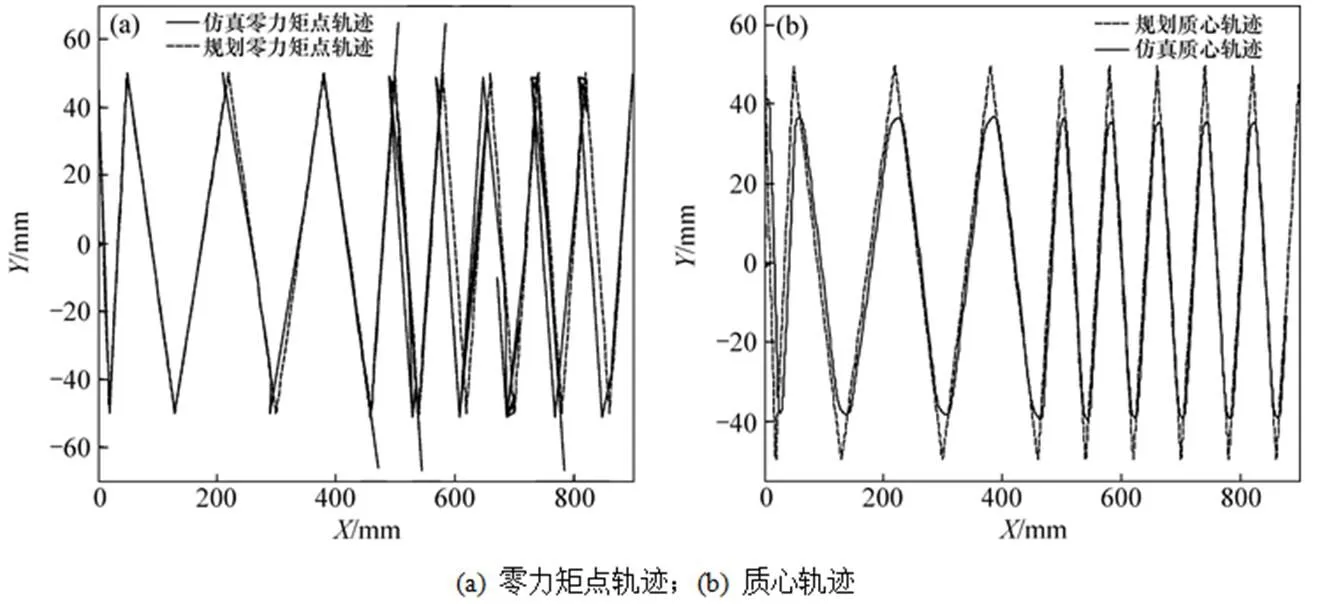
图7 机器人在斜坡工况下的轨迹对比图

图8 机器人在2种工况下的仿真结果

实验中，机器人在平地和斜坡2种工况下，足底接触力较仿真结果更平稳，波动幅度分别减少37.01%和59.94%；髋关节电流较仿真关节力矩更为平稳，波动幅度分别减少69.13%和62.75%，说明仿真环境中将上肢简化为等效质量块对机器人行走稳定性有所影响，且前述规划方法可以在实际平地和斜坡地面的真实环境中实现，其适应性较强。

图9 NAO样机

图10 平地工况下参数仿真结果和实验结果对比

图11 斜坡工况下参数仿真和实验结果对比

4 结论

1) 提出1种基于3-D步行序列的步态规划方法。

2) 完成平地工况下单足相、双足相的零力矩点轨迹以及足部踝关节轨迹规划，通过调整步态规划参数完成倾角为5°的斜坡的步态规划。

3) 实验中NAO机器人行走较仿真实验中更加平稳，故该规划方法是可行的，且对真实环境地面的适应性强。

[1] KAJITA S, MATSUMOTO O, SAIGO M. Real-time3D walking pattern generation for a biped robot with telescopic legs[C]//Proceedings 2001 ICRA. IEEE International Conference onRobotics and Automation. Seoul,South Korea: IEEE. 2001: 2299−2306.

[2] DASGUPTA A, NAKAMURA Y. Making feasible walking motion of humanoid robots from human motion capture data[C]// IEEE International Conference onRobotics and Automation. Detroit, USA: IEEE. 1999:1044−1049.

[3] FUJIMOTO Y, SMADI I A, WAKAYAMA Y. Development of musculoskeletal biped robot driven by direct-drive actuators[C]//2011 IEEE International Conference onMechatronics (ICM). Istanbul, Turkey: IEEE. 2011 :821-826.

[4] 王志良, 于国晨, 解仑. 基于解耦合成的及ZMP 方程的仿人机器人三维步态规划[J]. 计算机科学, 2010, 37(12): 215−217. WANG Zhiliang, YU Guochen, XIE Lun. Three-dimensional gait planning for humanoid robots based on decoupling synthesis and ZMP algorithm[J]. Computer Science, 2010, 37(12): 215−217.

[5] HUANG Weiwei, CHEW C M, ZHENG Yu. Pattern generation for bipedal walking on slopes and stairs[C]//8th IEEE-RAS International Conference onHumanoid Robots.Daejeon: IEEE, 2008: 205−210.

[6] ZHOU Changjiu, YUE P K, NI Jun. Dynamically stable gait planning for a humanoid robot to climb sloping surface[C]// IEEE Conference onRobotics, Automation and Mechatronics. Singapore: IEEE, 2004: 341−346.

[7] Nagasue J, Konishi Y, Araki N, et al. Slope-walking of a biped robot with k nearest neighbor method[C]//Fourth International Conference onInnovative Computing, Information and Control (ICICIC). Kaohsiung, Taiwan, China: IEEE, 2010: 173−176.

[8] ALI F, AMRAN A C, KAWAMURA A. Slope-walking of a biped robot with position and orientation based inverse kinematics method[C]//International Conference onControl Automation and Systems (ICCAS). Gyeonggi-do, South Korea: IEEE, 2010: 1724−1728.

[9] ALI F, SHUKOR A Z H, MISKON M F, et al. 3-D biped robot walking along slope with dual length linear inverted pendulum method(DLLIPM)[J]. International Journal of Advanced Robotic Systems, 2013, 11(10): 46−50.

[10] 张文. 仿人机器人斜面行走的步态规划[D]. 北京: 北京理工大学机电学院, 2015: 45−46. ZHANG Wen. A universal pattern generator for humanoid robots walking on slopes[D]. Beijing: Beijing Institute of Technology. School of Mechatronical and Engineering, 2015: 45−46.

[11] 杨璟. 仿人机器人斜面步行模式的建模与规划[D]. 杭州: 浙江大学控制科学与工程学院, 2012: 34−36. YANG Jing. Motion modeling and gait planning for humanoid robot walking on slopes[D]. Hangzhou: Zhejiang University. College of Control Science and Engineering, 2012: 34−36.

[12] 毕盛, 闵华清, 陈强. 一种仿人机器人斜坡运动步态规划方法[J]. 华南理工大学学报(自然科学版), 2010, 38(11): 148−154. BI Shen, MING Huaqing, CHEN Qiang. A kind of humanoid robot slope gait planning method[J]. Journal of South China University of Technology(Natural Science Edition), 2010, 38(11): 148−154.

[13] 张克, 傅佩琛, 强文义. 小波神经网络在两足步行机器人爬斜坡中的应用[J]. 机器人, 2000, 22(5): 384−389. ZHANG Ke, FU Peichen, QIANG Wenyi. Application of wavelet neural network in biped walking robot climbing slope[J]. Robot, 2000, 22(5): 384−389.

[14] 丁加涛, 肖晓晖, 王杨. 双足步行机器人在线步态生成与偏航控制策略[J]. 中南大学学报(自然科学版), 2016, 47(4): 1136−1143. DING Jiatao, XIAO Xiaohui, WANG Yang. Strategy for biped gait robot online generation and yaw control[J]. Journal of Central South University(Science and Technology), 2016, 47(4): 1136−1143.

[15] SANTACRUZ C., NAKAMURA Y. Walking motion generation of humanoid robots: Connection of orbital energy trajectories via minimal energy control [C]//11th IEEE-RAS International Conference on Humanoid Robots (Humanoids). Bled, Slovenia: IEEE, 2011: 695−700.

[16] Kajita S, Hirukawa H, Harada K. Introduction to humanoid robotics [M]. Berlin, Germany: Springer, 2005: 120−130.

[17] NIKU S. B. Introduction to robotics: analysis, systems, applications [M]. New Jersey: Prentice Hall, 2001: 50−500

[18] HONG Y D,LEE B J, KIM J H. Command state-based modifiable walking pattern generation on an inclined plane in pitch and roll directions for humanoid robots[J]. IEEE/ASME Transactions on Mechatronics, IEEE, 2011, 16(4): 783−789.

[19] MORISAWA M, KANEHIRO F, KANEKO K, et al. Reactive biped walking control for a collision of a swinging foot on uneven terrain[C]//11th IEEE-RAS International Conference onHumanoid Robots (Humanoids). Bled, Slovenia: IEEE, 2011: 768−773.

(编辑 伍锦花)

Gait planning and experimental study of biped robot based on 3-D walking sequence

CHEN Jianfang, DING Jiatao, XIAO Xiaohui

(College of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)

In order to improve the adaptability of biped walking in the real environment, a novel gait planning method based on 3-D walking sequence was proposed. By imitating human walking behaviour and taking the change of ground height into consideration, 3D walking sequence (WS), which also considers the rotational motion of ankle joint and the vertical height of the robot, was firstly defined. Then, during single support phase (SSP), optimal control (OC) theory and linear inverted pendulum model (LIMP) were adopted for generation of zero moment point (ZMP) trajectories. The 5th order spline interpolation was used to generate ZMP trajectories and to produce the center-of-mass (COM) height variation during the double support phase (DSP). By employing motion parameters of the foot, the foot trajectory was also obtained by piecewise continuous cubic Hermite interpolation. After that, the Newton-Raphson method was used to solve the desired joint angle. Finally, dynamic simulation and hardware experiments of bipedal walking on flat and slope ground were carried out by employing the NAO robot. The results show that the proposed method is effective in practice and that the robot walks more stably in the real environment. Fluctuation range of the foot contact force of NAO robot in flat and slope conditions decrease by 37.01% and 59.94% respectively compared with those in simulation test, and fluctuation range of the hip joint decrease by 69.13% and 62.75%, respectively.

3-D walking sequence; biped robot; gait planning; slope

TP242.6

A

1672−7207(2018)04−0831−08

10.11817/j.issn.1672−7207.2018.04.009

2017−04−15；

2017−05−29

国家自然科学基金资助项目(51675385，51175383)(Projects(51675385, 51175383) supported by the National Natural Foundation of China)

肖晓晖，博士，教授，博士生导师，从事移动机器人学与微操作机器人研究；E-mail：xhxiao@whu.edu.cn