基于电动力绳的火箭末级离轨系统设计及效能分析

王小锭，张 烽，董晓琳，张恒浩，吴胜宝

0 引 言

对于已经存在的太空碎片，主动清除方式主要有推力离轨方法、空间机器人抓捕离轨方法等，但是此类方法都存在耗能大、成本高的缺点。有计算结果表明，仅通过碎片轨道的自然衰减使碎片离轨耗时极长，因此迫切需要开发低耗、高效的碎片离轨、清除技术。此外，为了从源头上消除空间碎片的产生，在不远的将来所有发射入轨的火箭、卫星都应具备清理自身碎片的能力，在完成任务后实现主动快速离轨。

电动力绳系是利用系绳切割地磁场而产生电荷效应，其中绳系端部安装有电荷收集及发射器，当绳系与地球的磁层和电离层相互作用时，由于收集器和发射器与电离层之间存在电荷交换，绳系与电离层形成了一个闭合回路，因而在导电绳系中产生了电流[1～6]。电流回路在磁场中受到洛伦兹力作用，绳系利用这个力矩实现离轨。利用电动力绳系实现火箭末级离轨，离轨过程中不需要消耗火箭末级所携带的推进剂，可有效降低火箭末级重量，从而降低离轨成本，提高火箭末级的离轨效率。但是，电动力绳系如何结合运载火箭进行离轨工程化应用存在一些技术难点，离轨效能也是影响其可行性的重要方面，本文针对这些问题开展研究。

1 电动力绳系离轨的火箭末级适应范围分析

经研究分析，中国目前主要火箭末级需考虑采取离轨措施的火箭末级轨道及质量特性如表1所示。

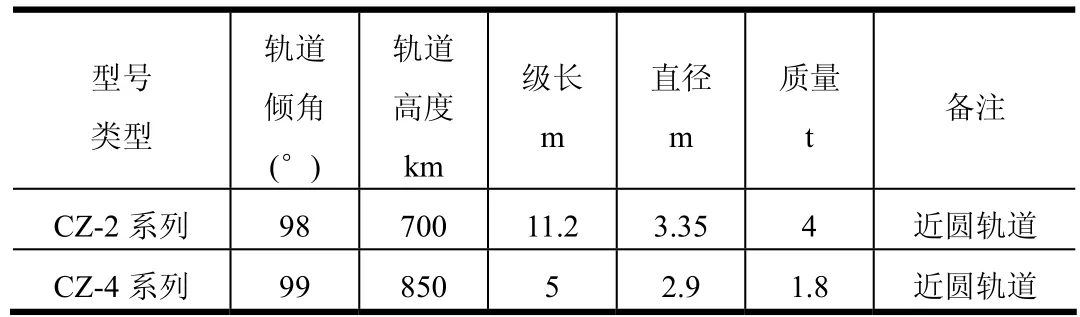
表1 中国主要火箭末级情况（需考虑离轨措施）Tab.1 Major Final Stages of Chinese Luanch Veichles (Need Deorbiting Measures)

通过研究表明，中国目前应用的典型火箭末级很难满足25年衰减的国际要求。考虑对这2种类型的火箭末级采用直接制动离轨方式，需要末级提供的速度增量及燃料消耗如表2所示。

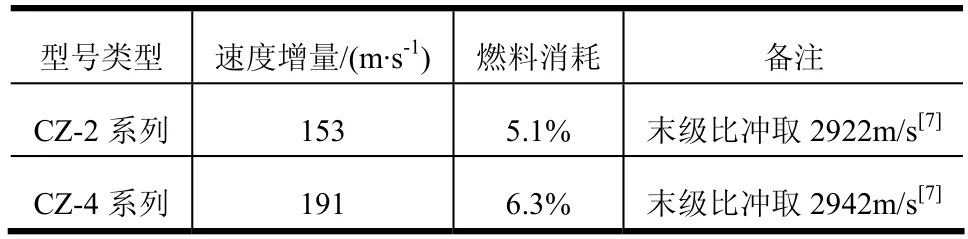
表2 直接离轨能力需求分析Tab.2 Active Deorbiting Requirements

CZ-2及CZ-4系列火箭末级情况，若采用主动离轨，需要的速度增量较大，意味着额外消耗较多的燃料，因此适用于电动力绳系离轨方式，该系列火箭总体参数相近，本文以CZ-2C为典型案例开展研究。

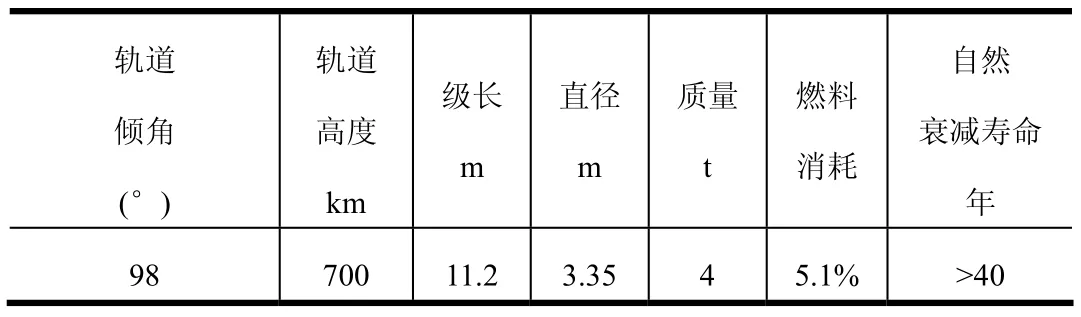
表3 CZ-2C火箭末级离轨任务参数分析[7]Tab.3 Deorbiting Paramenters of CZ-2C Final Stage

2 电动力绳系离轨系统设计

2.1 系统组成及工作原理

根据总体参数和指标约束，以SSO轨道CZ-2C为离轨目标，需要实现轨道倾角为98°、质量为4 t、级长为11.3 m、直径为3.35 m的火箭末级利用电动力绳系完成离轨（从轨道高度700 km降轨至200 km）。

考虑到火箭末级离轨系统要做到系统尽量简单，以避免设计的复杂度和系统开销代价。因此，在满足总体任务指标要求的情况下，控制策略采用简单易行的方式。

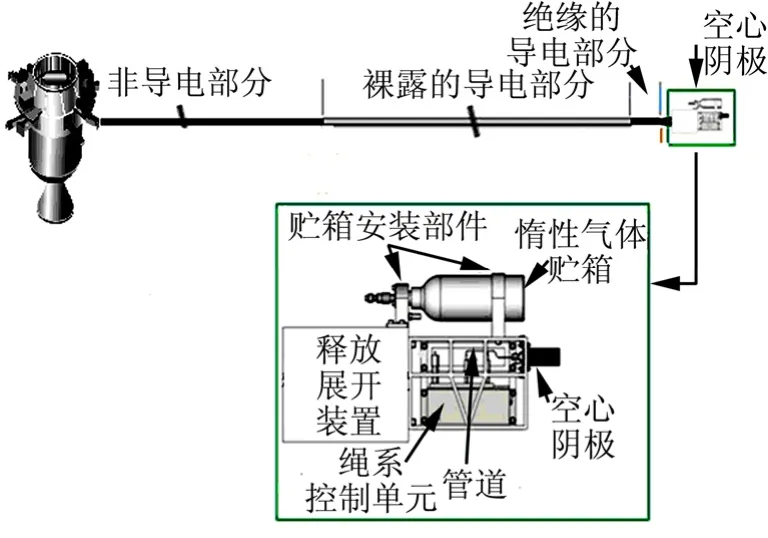
图1 电动力绳离轨系统组成Fig.1 Composing of Electrodynamic Tethered Deorbiting System

基于电动力绳的火箭末级离轨系统由火箭末级离轨模块、电动力绳系组成，电动力绳系包括释放展开装置、导电绳系、绳系控制单元、电荷发射装置等部分，电动力绳离轨系统工作原理如图2所示。

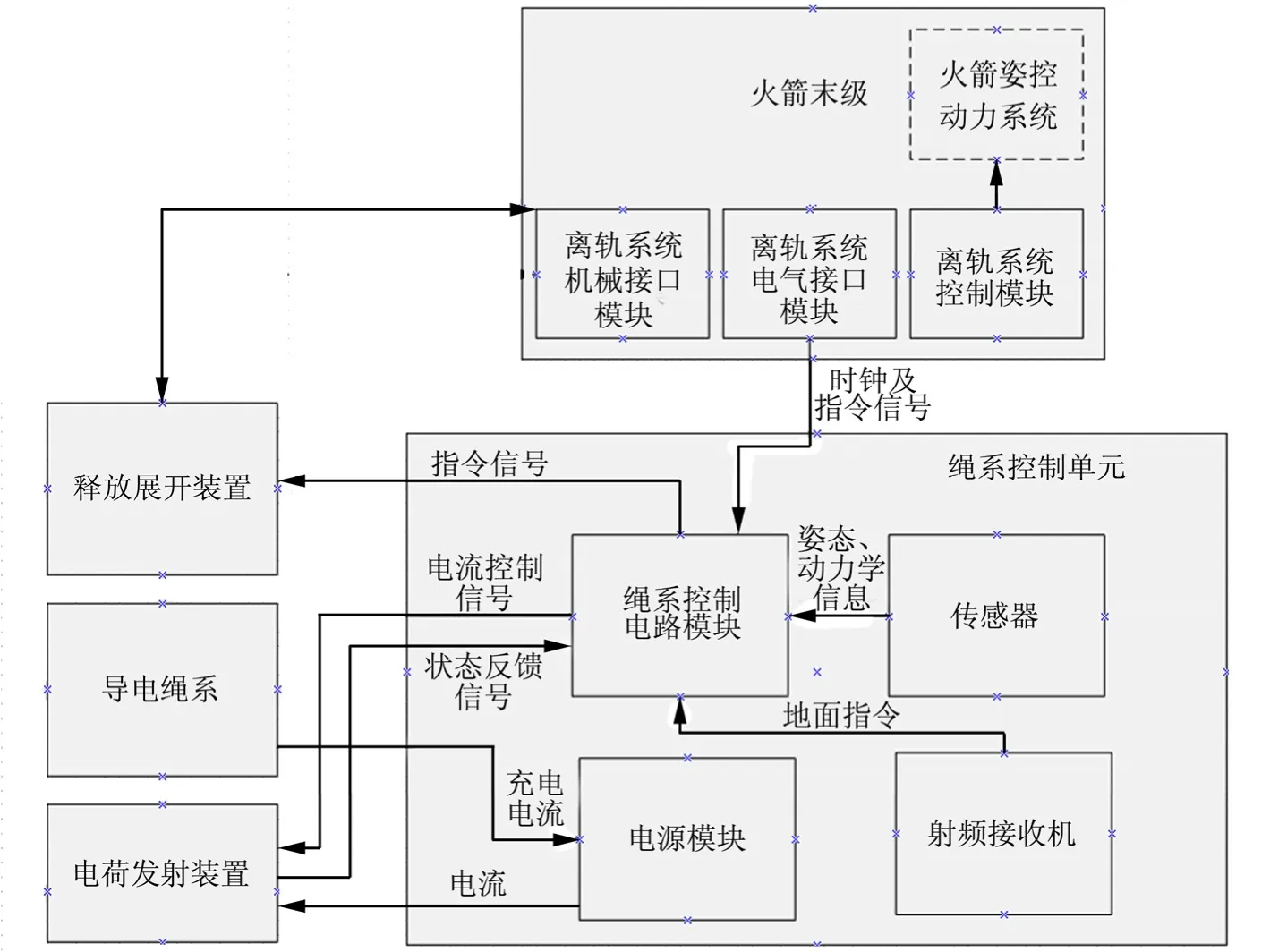
图2 电动力绳离轨系统工作原理Fig.2 Principium of Electrodynamic Tethered Deorbiting System

火箭末级离轨模块为电动力绳系提供指令和时钟信号，并为释放展开装置提供机械接口。绳系控制单元接收指令并控制释放展开，同时根据状态反馈控制绳系电流，接收导电绳系的充电电流进行充电，以提供任务期间各部件的电源。绳系控制单元通过接收机能够接收地面遥控指令信号。

电动力绳系离轨系统采用裸绳系技术和空心阴极技术实现高效电荷交换，绳长5 km，设置空心阴极发射电流1 A，末端载荷质量不超过40 kg。

2.2 导电绳系

绳系由3个部分组成：非导电部分、裸露的导电部分以及绝缘的导电部分。

为了防止放电现象的发生，绳系靠近火箭末级的部分是一小段非导体绳系，是由抗拉能力强、电绝缘性好以及低密度的材料组成。非导电部分增加了稳定性，同时尽量减少额外的质量。

当绳系导电部分的一部分被裸露用来收集电子时，电位将减小由于电子的收集所产生的电动势，从而形成电流，直到绳系和空间电势平等。一旦发生这种情况，系绳开始吸引离子和减小电流。电子收集大于离子收集，由于离子的质量和大小比电子大，所以引起离子移动较慢，以至于离子的收集不足以在模型中显现。

绳系的导电部分到端块的最后的部分长度被绝缘，以防止电子与来自阴极等离子接触器发射的离子绳系被直接收集。

进入离轨阶段后，空间微流星和碎片的撞击有可能造成绳系断裂，绳系的张力过大也会对绳系造成危险。因此，要对绳系的结构进行合理的设计以减小断裂的风险，以提高生存能力。根据初步技术研究，绳系设计必须保证其在较长的任务周期中的存活率达到95%～98%。为保证绳系存活率，采用Hoytether方案，它由几股绳束编织而成，其结构为几条平行绳束，在中间有周期性相连，可以为载荷和电流提供冗余路径，以便在几股绳束断裂的情况下仍能保持设计载荷。

2.3 释放展开装置

在存储系统上，从技术成熟度上，采用卷轴式的绳系存放具备较高的成熟度，但其主要适用于圆柱状绳系，而对于带状绳系，可以重点考虑矩形箱式存放装置，但是需要对长度测量及速度控制进一步研究。

在弹射系统上，考虑采用弹簧进行弹射，为利于绳系展开释放的控制精度，可考虑采用伺服机构，以便进行弹射方向的控制；在制动系统上，考虑在绳系末端包裹摩擦材料达到减速目的。

释放展开装置通过释放机构与火箭末级相连接。当进行离轨操作时，绳系控制单元接收指令，启动绳系释放机构，由触发释放机构弹出绳系，控制绳系的释放速度，确保绳系展开的构型。由裸绳系收集电子，并将空心阴极安装在电动力绳系离轨装置的远端位置，由其发射收集的电子，以形成持续稳定的电流，从而产生离轨所需的洛仑兹力。

2.4 电荷发射装置

电荷发射装置即等离子接触器，这里采用空心阴极方案，空心阴极由一个阴极管、触发保持极、加热器和可封闭式通道等组成。工作气体 Xe流入阴极管内，在阴极顶限流小孔的作用下，阴极管内的压力通常要比小孔外的压力高几个数量级，约1～2 kPa。利用加热器将加热体缓慢加热到适当温度，在触发保持极对阴极加大约数百伏点火电压后，在发射体和触发保持极之间产生气体放电。

空心阴极系统设计分为 3部分，主要为：气路模块、电源转换模块（含测控模块）和电源系统设计。气路模块为空心阴极等离子体接触器提供必要的放电工质，电源转换模块将进入内系统的总线电压转换为各用电器所需的工作电压。电源系统对电源转换模块（含测控模块）进行供电，电源转换模块（含测控模块）控制气路的开关并完成相关数据测量，同时可以维持等离子体接触器点火，从而实现空心阴极系统与外界环境等离子体的电荷交换功能。

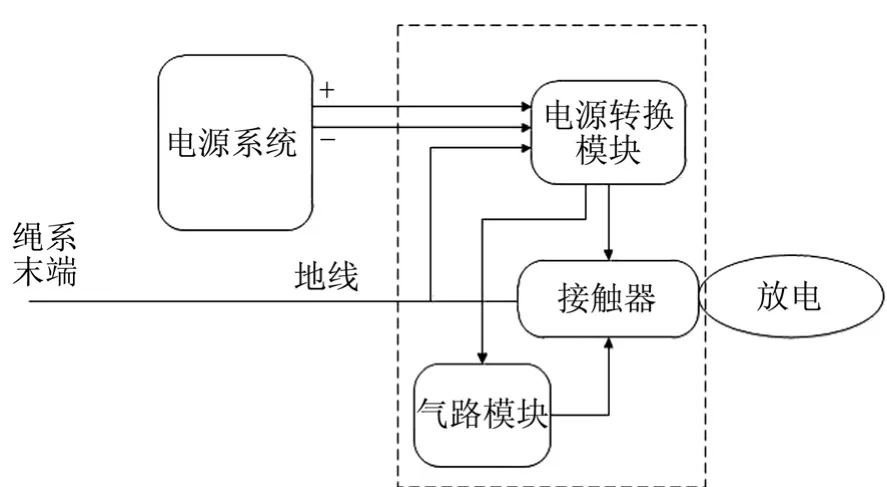
图3 空心阴极系统示意Fig.3 The System of Hollow Cathode

3 电动力绳系离轨系统对火箭末级技术需求

3.1 结构系统技术需求

根据电动力绳系离轨系统总体方案，结构系统需要考虑电动力绳系未释放展开时的存储和防护，并提供安装接口，在释放展开过程中，需要设计机构装置弹射出电动力绳系。因此，火箭末级结构系统主要需要考虑存储释放装置以及绳系对系统的需求。

针对一定的绳系结构设计和展开释放装置结构设计，需对其予以估重，使得运载火箭末级可承受此部分重量。根据绳系质量模型，对于5 km的电动力绳系离轨系统，其电动力绳系系统质量约57 kg，其中展开释放装置及其他系统装置约37 kg，绳系约20 kg。

采用卷轴式的展开释放装置可引起较小的失败，同时缠绕的风险和绳系扭曲的风险都较小。根据典型的展开释放装置估算，装置的安装接口为 670 mm×710 mm×120 mm。结合CZ-2C的布局构型，安装位置宜选在仪器舱外壁上以满足气动等性能，可将其布置于舱壁外，以利于展开释放动力学的位置。

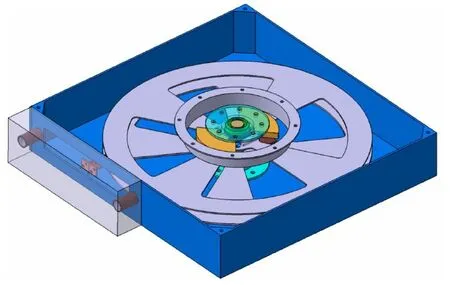
图4 典型的卷轴式展开释放装置示意Fig.4 Typical Reel Deployer

3.2 姿控系统技术需求

由于绳系具有阻尼小、柔性大的特点，在绳系释放过程及末级离轨过程中，绳系长度的变化引起Coriolis加速度，可能导致绳系出现大幅摆动及振动，进而与火箭末级相互作用时极易产生一系列复杂的耦合天平动及振动。特别是若不施加控制，绳系可能发生大幅度松弛振动，造成绳系缠绕、冲击等有害现象，并可能使得绳系动应力幅值超过材料的强度极限。此外，由于载荷弹射冲量必定导致火箭末级刚体产生反作用角动量，导致火箭末级刚体旋转。弹射飞行阶段绳系拉力为零或很小，基本不对火箭末级刚体姿态运动产生恢复力矩，而弹射绳系展开过程的拉力波动显著，因此有必要在弹射释放阶段对火箭末级姿态进行控制，否则火箭末级可能发生翻滚。

为确保火箭末级本体姿态摆动幅度较小，适合绳系弹射释放，应尽可能保证火箭末级纵轴与轨道径向一致，同时姿态角速度较小。在绳系释放过程中，火箭末级姿态与当地垂线偏离角度要求不超过90°，否则，本体发生翻转，将破坏绳系释放的稳定性。通过对弹射释放阶段的仿真分析，可以得到下述结论：若弹射初始时刻，经过弹射前的姿控过程，火箭末级本体姿态角速度不超过0.1 (°)/s，纵轴偏离当地垂线角度不超过25°时，或火箭末级本体姿态角速度不超过0.05 (°)/s，纵轴偏离当地垂线角度不超过32°时，无需使用额外的火箭姿控系统，采用下述释放策略，不会引发火箭末级的大幅翻转，绳系释放能够基本稳定。

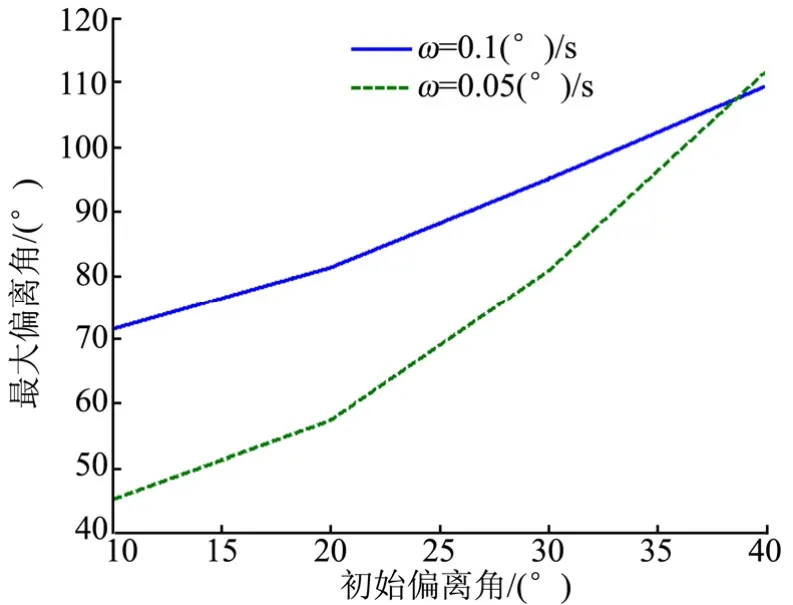
图5 火箭末级姿态偏离最大值变化趋势Fig.5 Maximum Diaviation of the Attitude

3.3 时序控制技术需求

CZ-2C火箭末级在电动力绳系作用下进行离轨运动。在离轨工作过程中，火箭末级系统工作过程需要根据控制系统的时序要求进行电信号控制。火箭末级电气系统应增加与绳系的接口电路，包括一路计时检查电路和一路指令接口电路。末级控制系统应对飞行软件进行适应性改进，增加末级任务后的姿态控制及时序控制。

4 电动力绳系离轨系统效能分析

4.1 动力学建模及离轨控制策略

基于电动力绳的火箭末级离轨任务主要分为绳系弹射释放和电动力离轨两个阶段。在弹射释放过程中，特别是无控释放情形，柔性绳系将产生大幅度运动，构型变化比较显著，故而采用“珠式”模型研究系绳释放过程[8,9]。记火箭末级为结点 0，沿火箭末级至载荷方向将绳单元的集中质量点依次记为结点1，2，…，n，记载荷为结点n+1。

图6 离散的系绳单元Fig.6 Discrete Units of the Tether

依据牛顿第二定律，可列出火箭末级（载荷）质心动力学方程表达式

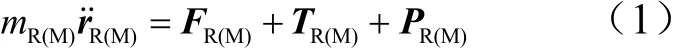
式中 mR(M)为火箭末级端（载荷端）的总质量，为火箭末级（载荷）的质量，me为绳系单元质量， nR(M)为火箭末级（载荷）内的绳系结点数； rR(M)为火箭末级（载荷）质心的位移矢量；FR(M)和 TR(M)分别为火箭末级（载荷）受到的地球万有引力主矢与系绳拉力；R(M)P 为外界摄动力。

火箭末级（载荷）外部绳结点的动力学方程为

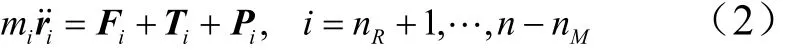
式中 Fi为结点i所受的万有引力矢量；Ti= Ti,i−1+Ti,i+1，Ti,i−1和 Ti,i+1分别表示结点i的前端结点 i −1和后端结点i+ 1 对其的拉力，而 Ti,i−1= EA(ηi,i−1−1 + αdη ˙i,i−1)，ηi,i−1为结点i与结点i−1间的系绳延伸率，αd为系绳的阻尼耗散因数，ηi,i−1为系绳段Li,i−1的延伸率；Pi为各结点收到的外界摄动力。对于结点 nR+1，其前端是火箭末级结点R，而结点 n −nM后端为载荷结点M。

离轨过程中，将火箭末级与末端载荷视为质点，电动力绳系视为刚性杆，离轨过程中忽略杆的刚体姿态并视其始终垂直于地球表面，因此动力学模型可描述为轨道参数缓慢变化的轨道摄动方程。为避免计算奇异，适应轨道倾角0°≤i＜180°和任意轨道偏心率的情况，针对传统的轨道六要素（半长轴a，偏心率e，轨道倾角i，升交点赤经Ω，近地点幅角ϖ，真近点角ν），引入六个非奇异轨道元素：

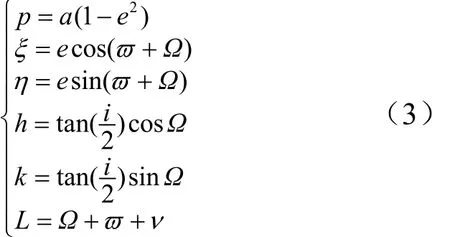
相应的轨道摄动方程为

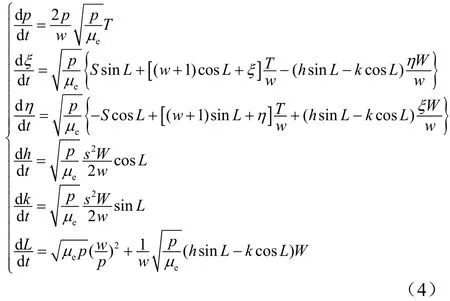
式中 S，T，W分别是沿轨道坐标系三个轴向的摄动加速度分量；µe为地球引力常数；s2=1+ h2+ k2；w=1 + ξ c o s L + η sinL。主要的轨道摄动力来源包括大气阻力、地球扁率、洛伦兹力等。

在电动系绳弹射释放阶段（特别是弹射飞行阶段）对火箭末级进行姿态控制，以避免火箭末级大幅摆动对系绳释放形成干扰，在绳系释放的 2个阶段拟采用下述释放控制策略：

a）绳系初始弹射阶段：绳系系统无控；

b）绳系主动释放阶段：绳系系统采用Kissel释放控制律。

初始弹射阶段火箭末级姿态变化曲线及主动释放阶段火箭末级姿态变化曲线分别如图7、8所示。

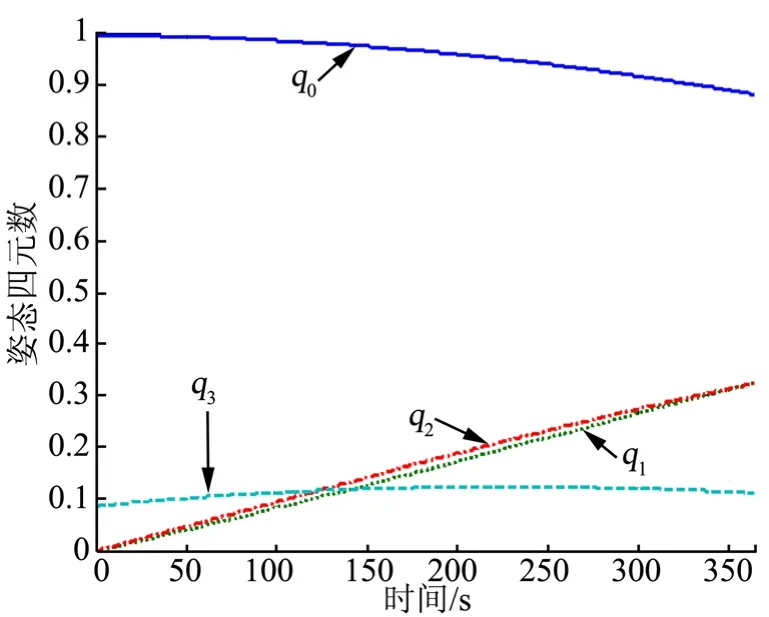
图7 初始弹射阶段火箭末级姿态变化曲线Fig.7 Attitude Variation of the Stage during the Intial Injection

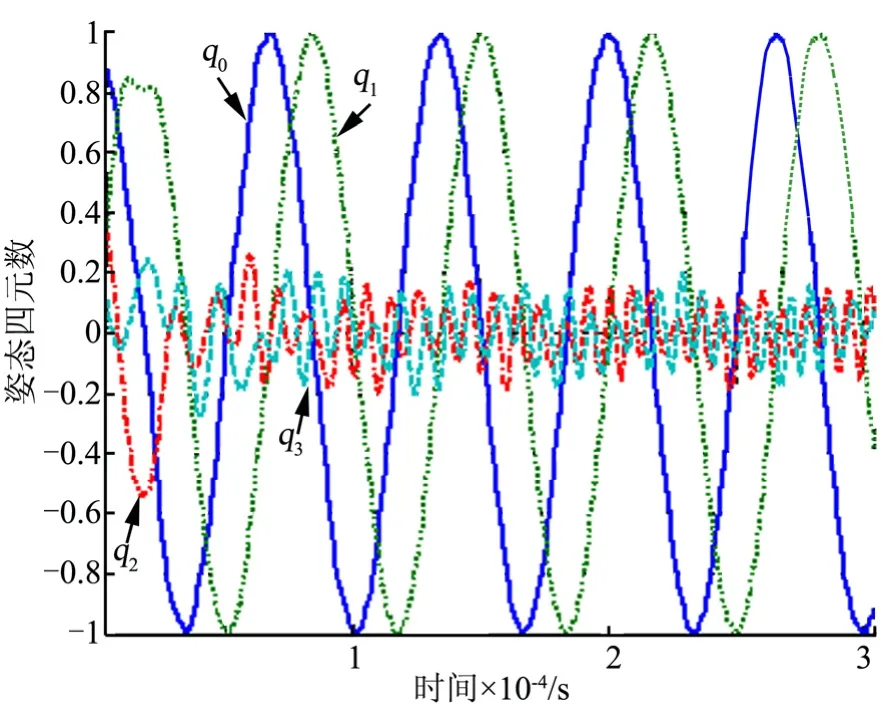
图8 主动释放阶段火箭末级姿态变化曲线Fig.8 Attitude Varation of the Stage during Active Deployment

通过仿真可以看出，初始弹射阶段时间较短，火箭末级在姿控作用下向目标值迅速趋近。在主动释放阶段，针对绳系系统采用Kissel控制律，绳系能够稳定释放，同时火箭末级姿态并未发生翻转，姿态能够保持稳定。

为保证在电动力辅助离轨阶段，绳系不发生大幅摆动，而且能够实现系统降轨，采用电流开断离轨控制律作为组合体姿态稳定控制策略，该方法算法简单，易于工程实现。

4.2 仿真系统构建

仿真系统包括参数模型数据库、电动力计算模块、绳系与火箭末级耦合动力学模块、离轨轨道计算模块等。其中，参数模型数据库采用第11代国际地磁场参考场（IGRF11）13阶模型计算磁场强度，采用国际参考电离层模型 IRI2007计算电子密度，采用美国海军研究实验室（NRL）发展的NRLMSISE-00大气模型计算大气密度。离轨过程仿真计算流程如图9所示。

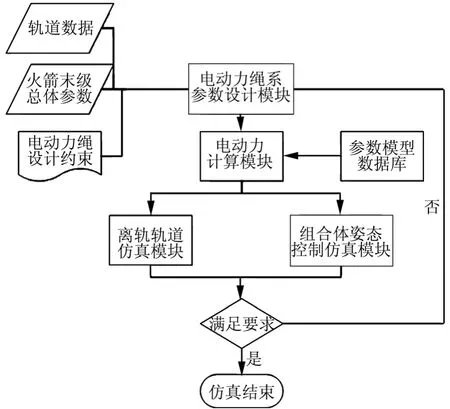
图9 火箭末级离轨任务仿真计算流程Fig.9 Simulation Flow of the Deorbit Mission

4.3 离轨效能分析结果

对于采样电动力绳系离轨的系统，影响其离轨的时间因素除轨道高度、轨道倾角、电动力绳长度之外，还有系统重量等其他因素。不计绳系系统的姿态变化，火箭末级质量参数与几何参数按CZ-2C作为标称值，标称值基本参数如表4所示。同时考虑地球引力摄动及大气阻力，采用刚性杆系绳模型对离轨过程进行分析，假设系统构型始终沿轨道径向保持稳定，对绳系离轨过程进行性能指标分析。

表4 标称值基本参数Tab.4 Basic Parameters

图10描述了系统轨道高度、轨道偏心率、电子密度、动生电动势、阴极电流及系绳平均电流随时间变化情况。不难看出，此时系统的离轨耗时约 145天，轨道偏心率几乎没有变化，电子浓度保持在1011量级，动生电动势在700～1200 V范围内变化，阴极电流即系绳最大电流达到4.5 A，平均电流随着离轨过程的进行由0.5 A增大到3 A。

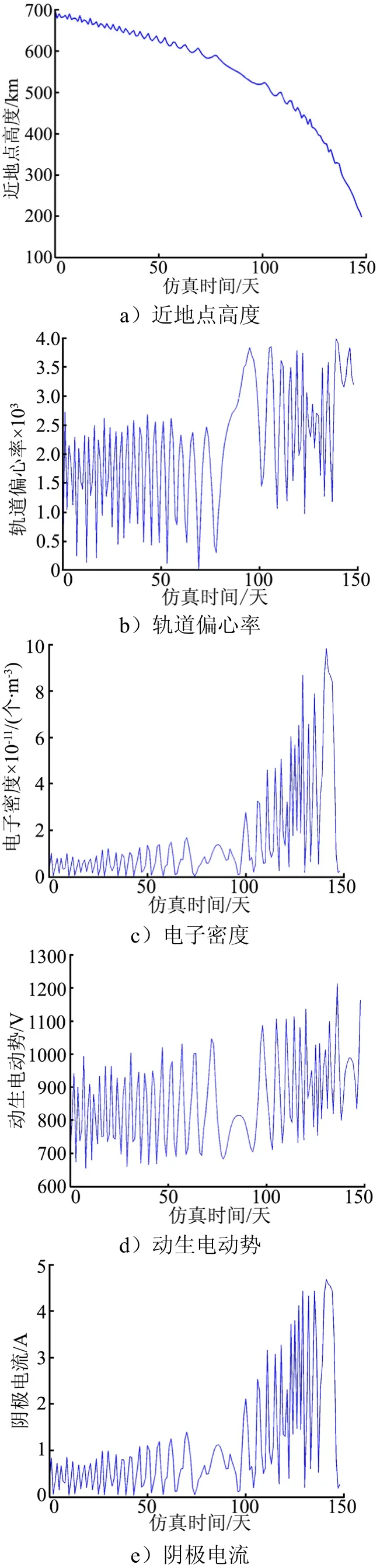
图10 标称算例各参数随时间变化情况Fig.10 The Variation of Parameters for the Nominal Case

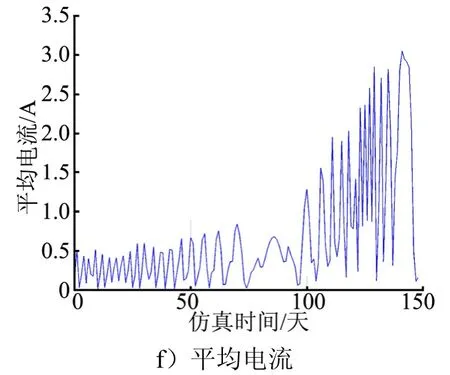
续图10

以CZ-2C火箭末级为对象，采用不同的绳系长度情况下，针对不同绳长参数，分别仿真计算离轨时间效能，得到各种工况下离轨时间，如图11所示。

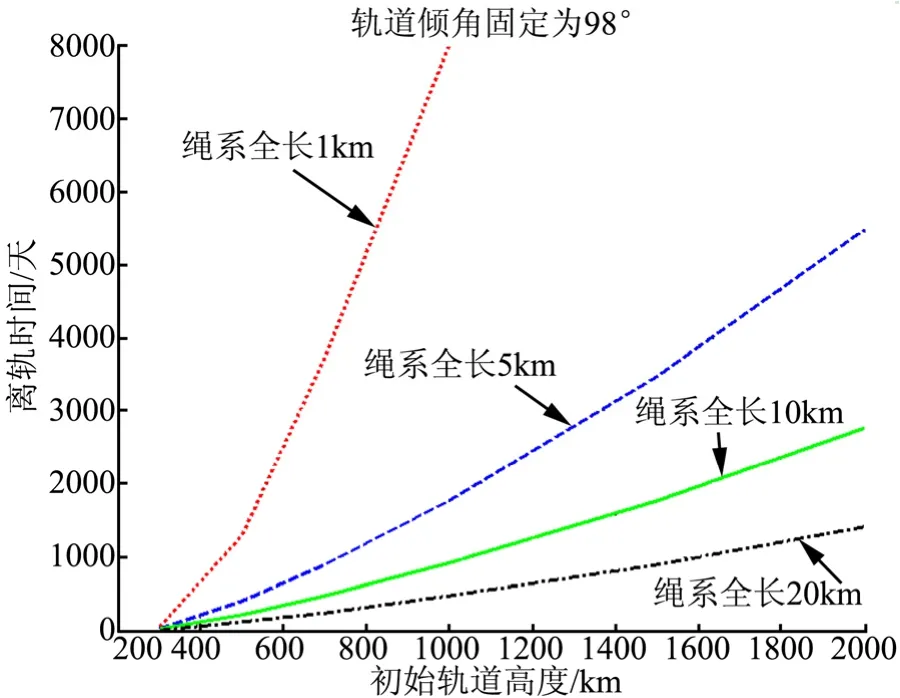
图11 多组绳长工况下离轨时间与初始轨道高度关系曲线Fig.11 The Relation Curves That the Deorbit duration Varies with the Initial Orbital Altitude

由图11可以看出，假定于CZ-2C火箭末级为离轨对象，设计5 km的绳系长度，即可实现700 km SSO CZ-2C火箭末级在3年内离轨。

给定火箭末级，对于不同的离轨时间要求，电动力绳系统的适应范围也会不同，对于离轨时间要求为25年以及离轨时间要求为5年的两种情况下，绳系长度为5 km时，通过仿真计算，得到电动力绳的适应范围如图12所示。

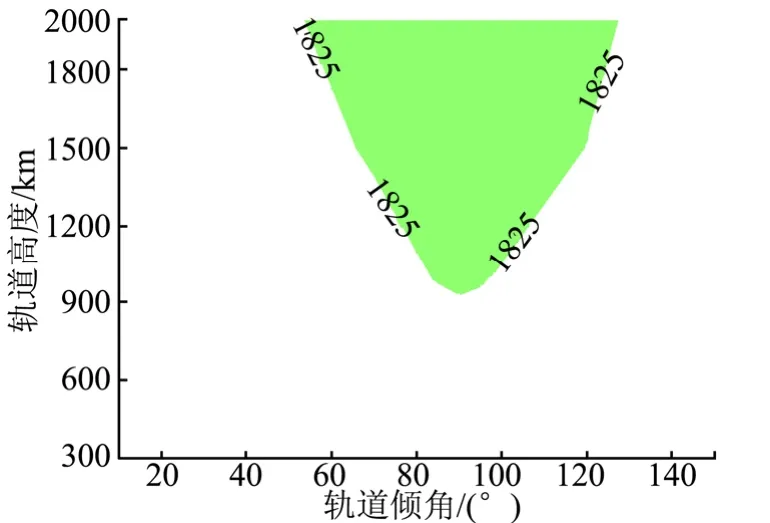
图12 5km绳系的适应范围Fig.12 Admissiable Range for 5km Tether

由图12可以看出，如果以5年为时间限制要求，则5 km绳系的适应范围为图13所示线条以下部分，覆盖轨道高度300～2000 km，轨道倾角60°的大部分轨道，当轨道倾角为98°时，覆盖轨道高度900 km以下的轨道。

5 结束语

针对电动力绳系在火箭末级离轨中的应用，本文系统分析了适用于电动力绳系离轨的火箭末级参数特性，对电动力绳离轨系统进行设计，对火箭的技术需求进行可行性分析，针对设计方案开展动力学建模及控制策略分析，最后通过仿真完成离轨系统效能分析，经仿真分析，电动力绳应用于火箭末级离轨，能够极大提高离轨效率，离轨时间效能满足国际空间碎片减缓要求。