姿控发动机小推力测量天平设计
寇 鑫,李广会,王宏亮,刘丽宁
(西安航天动力试验技术研究所,陕西 西安 710100)
0 引言
姿控发动机试验小推力测量的关键技术在于设计合适可靠的推力测量与校准装置,保证适当刚度的前提下发动机产生的推力应最大限度地传递到测量传感器上。单分力天平使发动机产生的推力通过杠杆和弹性转轴转换为力矩,再将应变梁设计于力臂较小的位置,在发动机相同推力的量级下,大幅增加应变梁的变形量,提高推力测量装置的系统灵敏度。
国内外对于微小发动机试验室推力测量采用的方法和装置各异。如美国NASALewis研究中心采用弯曲位移电磁力补偿、比例微积分电路控制方法测量Arcjet的推力;俄罗斯原子能研究所采用钟摆位移电磁力补偿方法测量微小推力等,但是这些装置存在测量精度较低、价格高等问题。北京航空航天大学与航天某所合作[4],研制出天平结构的小推力测量台架,其推力量级为0.015~200 mN,但只能进行短程试验测试。
目前推力量级4~25 N的姿控发动机推力测量存在的主要问题是:由于管路、测量线缆的约束力“消耗”掉部分推力,试验过程温度与振动的影响及推力架结构形式、传感器安装等因素,导致实验室内校准的传感器系数不能准确反应出发动机实际工作过程情况和环境条件,影响测量结果的准确性。因此,研究新的测力结构装置和现场校准方法是提高小推力测量准确性的有效途径。
1 单分力天平测量原理
研制的一种新型单分力天平测力机构采用杠杆原理(图1),发动机产生的推力通过杠杆和弹性转轴转换为力矩,再将应变梁设计于力臂较小的位置,从而在发动机相同的推力量级下,增加应变梁的变形量,提高测量装置的系统灵敏度。
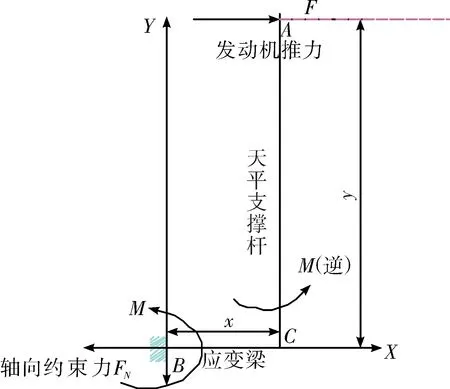
图1 单分力天平受力原理简图Fig.1 Force principle of single-component balance
上述结构钢架可由如下算法求得应变梁上的正应力,并求得梁上应变:根据钢架的外力特征,可判断AC杆(天平支撑件)发生的是弯曲变形,BC杆(应变梁)发生的是弯曲和拉压组合变形。
立柱段(AC杆),受力根据受力平衡条件,有如下关系:
Fs(y)-F=0,Fs(y)=F,(0 式中:Fs为剪切力;h为天平支撑杆高度。 由于AC杆只发生弯曲变形,其上只存在正应力,正应力σ1和表面应变ε1可由下式计算得到: 式中:Wz为AC杆的抗弯截面系数;E为材料弹性模量。 对于BC杆,根据受力平衡条件,有如下关系: ∑Fx=0⟹F-FN=0⟹F=FN ∑Mx=0,M(逆)=M(顺)=F·y(顺) BC杆由轴向约束力产生的拉应力σ2和正应变ε2分别为: 式中:A为横截面积;E′为弹性模量。 由弯曲产生的正应力σ3和正应变ε3分别为: 根据叠加原理[9],得到BC杆总的正应变εBC= 由上述理论分析可知,若被测发动机推力F较小,而当天平支撑件高度y越大,应变梁弹性模量E′越小时,应变梁应变也越大,故设计合理的单分力天平结构,并选择合适的应变梁可以有效提高传感器的灵敏度,为提高小推力测量精度创造条件。 本研究中针对最大推力为25 N的小姿控发动机进行天平结构设计。由于单分力天平量程较小,在发动机安装、推进剂管路安装等环节很容易导致应变梁过载损坏。因此,在天平设计时设计了过载保护装置,如图2所示。在应变梁上粘贴有电阻式应变片,粘贴时应尽量靠近应变最大位置,从而将应变梁的应变转换为电信号输出,如图3所示。 图2 单分力天平结构图Fig.2 Structure of single-component balance 图3 单分力天平应变片粘贴Fig.3 Stickup of strain gage for single-component balance 转接架设计成L型,一端与发动机连接,另一端与天平连接。在转接架上与发动机轴线同心的位置设计校准力加载点。为了保证发动机未点火状态下单分力天平处于零位,转接架与天平之间的相对位置可以调整,在转接架的右侧设计平衡块,通过更换平衡块来辅助调整天平零位。 设计的单分力天平小推力测量方案采用的是梁式弹性结构,在相同量级推力条件下,其较传统的弹簧片结构有更大的应变。利用有限元结构分析软件对天平的设计进行校核分析,文献[5]采用有限元分析方法对六分盒式天平的优化设计进行了研究。为比较设计的测量结构与传统的弹簧片测力结构的优劣,以应用较多的10 N和25 N量级推力对两种测力结构进行了力学分析。 由于应变产生的形式不同,对比分析了单分力天平应变梁的等效应变及弹簧片的切应变,应变云图分别如图4和图5所示。 图4 单分力天平10 N等效应变Fig.4 10 N equivalent strain of single-component balance 图5 弹簧片10 N剪切应变Fig.5 10 N shear strain of leaf spring 单分力天平在10 N推力加载的条件下其应变梁位置发生最大变形,最大等效应变量为282 με,弹簧片最大应变发生在轮辐位置处其最大剪切应变为44 με。由此可见,当发动机推力为10 N时,单分力天平应变约为传统弹簧片应变的6倍。 单分力天平在25 N推力加载的条件下其应变梁位置发生最大变形,最大等效应变量为705με,弹簧片最大应变发生在轮辐位置处,其最大剪切应变为110 με,单分力天平应变约为传统弹簧片应变的6.5倍。 由此可见,在同等推力量级的作用下,相比传统弹簧片应变式传感器,单分力天平可以产生数倍量级的应变,从而可以明显放大由推力作用所产生的电信号,显著提高该推力量级下的测力灵敏度。 发动机推力通过转接架传递给测量力传感器,传感器输出经调理后传送给采集系统。由于管路、测量线缆的约束力会“消耗”掉部分推力,因此测量力传感器测量到的真实力值小于发动机推力,在实验室内调试校准的传感器系数不能准确反应出发动机的实际推力。因此,采用该测量装置进行推力测量时,需要进行现场原位校准。针对单分力天平测力方案,设计推力测量校准一体化装置,结构见图6,采用此装置对单分力天平进行了校准测试。 图6 稳态推力测量校准一体化装置结构示意图Fig.6 Structure diagram of integrated calibration device for steady state thrust measurement 原位校准装置在试车前模拟发动机推力对“测量力传感器”进行原位校准。整个校准过程中所有线缆、增压管路在推力作用下的变形以及所“消耗”的力与试验状态保持一致,其中“测量力传感器”是被校准对象。 推力校准时,由计算机内的校准软件通过控制系统控制力源施加力值,同时采集系统实时采集经过信号放大器放大的标准力传感器信号,当两者差值在一定区间稳定后,同时记录“标准力传感器”和“测量力传感器”的输出值,实现自动校准,即通过“标准力传感器”对“有约束的测量力传感器”进行校准[10-11]。 基于上述推力测量校准原理,在不同温度环境下,针对10 N推力进行了单分力天平测力校准测试。在不带管路约束,装置工作环境温度为13 ℃(调试环境温度)条件下,对单分力天平进行10 N快速校准,采用3遍11档加载卸载调试方式对测量力与标准力数据进行线性拟合分析。 标准力Fs与天平测力Fc之间存在如下线性关系: Fs=b·Fc 校准曲线斜率b表征测量力传感器至标准力传感器的传递系数,b值越接近于1,表示传递效果越好。通常情况下由于外界约束力值损耗,测量力是小于标准力的,故一般b值是大于1的。10 N加载条件,带管路约束,环境温度分别在22 ℃,42 ℃,62 ℃和82 ℃时的标准力-测量力拟合曲线如图7所示。对应的力值传递系数见表1。 图7 标准力-测量力拟合曲线Fig.7 Fitting curve of standard force-measured force 环境温度/℃22426282力值传递系数1 04251 03531 02751 02 由力值传递系数随环境温度变化曲线可以看出,随着环境温度的升高,系数不断减小,说明测量系统传递精度会受到环境温度影响,基于远程自动原位校准技术,校准时的温度与试验过程中一体化装置所处的温度一致,可有效提高小推力的测量精度。 推力测量装置在推力测量过程中引入的不确定度主要有:现场校准引入的不确定度、测量力传感器引入的不确定度、温度变化引入的不确定度。 合成标准不确定度计算公式如下: 扩展不确定度计算公式如下: U=kub 式中:u标为校准传感器引入的标准不确定度;u传为测量力传感器引入的标准不确定度;u测为测量系统引入的标准不确定度;u温为温度变化引入的不确定度;c为级差系数;k为包含因子。 各个环节引入不确定度分析:校准传感器引入的标准不确定度为u标:0.05%。 测量力传感器引入的标准不确定度u传:测量力传感器为非标研制,其测量精度为0.1%。 测量系统引入的标准不确定度u测:数据采集系统采用电压采集模块,该模块电压参数测量的不确定度为u测=0.1%。 则采用该装置进行25 N推力测量时,温度变化引入的相对标准不确定度为: 经对各环节分析计算,最终得ub=0.2%。测量装置的扩展不确定度为:U=0.5%。 针对4-25 N推力小发动机设计了基于单分力天平的校准测量一体化装置,对单分力天平和传统方式测量推力的方式进行了力学仿真分析。采用推力测量校准系统,在不同环境温度条件下对单分力天平进行推力校准测试,验证了单分力天平在姿控发动机小推力测量中应用的可行性。经过现场调试,在22~82 ℃范围内,小推力测量装置扩展不确定度优于1%,测量系统指标满足设计要求,解决了4-25N量级小推力精确测量的难题。 参考文献: [1] HANG T W,CURRAN F M. Arcjet starting reliability: a multistart test on hydrogen/nitrogen mixtures: AIAA 87-1061 [R]. USA: AIAA,1987. [2] WILLMES G F,BURTON R L. Performance measurements and energy losses in a 100 Watt pulsed arcjet: AIAA 96-2966 [R]. USA: AIAA,1996. [3] 吴汉基,冯学章.地球静止卫星南北位置保持控制系统的选择[J].中国空间技术,1994(5):17-24. [4] 汤海滨,刘畅. 一种微小推力测量试验台架设计[J]. 推进技术,2001,22(2):174-176 [5] 张铮铮,许国伟,王文涛. 盒式单分力天平优化设计[J]. 舰船科学术,2009,31(5):121~125. [6] 江洪. SolidWorks有限元分析实例解析[M ].北京: 机械工业出版社,2007. [7] 郭霄峰. 液体火箭发动机试验[M]. 北京: 宇航出版社,1990. [8] 熊诗波.机械工程测试技术基础[M]. 北京: 机械工业出版社,2009. [9] 刘鸿文. 材料力学[M].5版.北京: 高等教育出版社,2010. [10] 岑乐观. 小推力姿控发动机的推力测量[J]. 中国电子学术期刊出版社,1994-2013:55~61. [11] 刘万龙,朱昊伟,孙树江,等.国内微推力测试技术发展现状[J]. 火箭推进,2015,41(5):7-11. LIU Wanlong,ZHU Haowei,SUN Shujiang,et al. Development status of micro-thrust testing technology in China [J]. Journal of rocket propulsion,2015,41(5):7-11.


2 结构设计与仿真分析
2.1 结构设计


2.2 测力仿真分析


3 测量与校准装置设计与调试
3.1 测量与校准装置设计

3.2 性能测试


3.3 测量装置不确定度预估


4 结 论

